数学人教A版(2019)选择性必修第二册第四章 数列 单元整体复习课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册第四章 数列 单元整体复习课件(共20张ppt) | 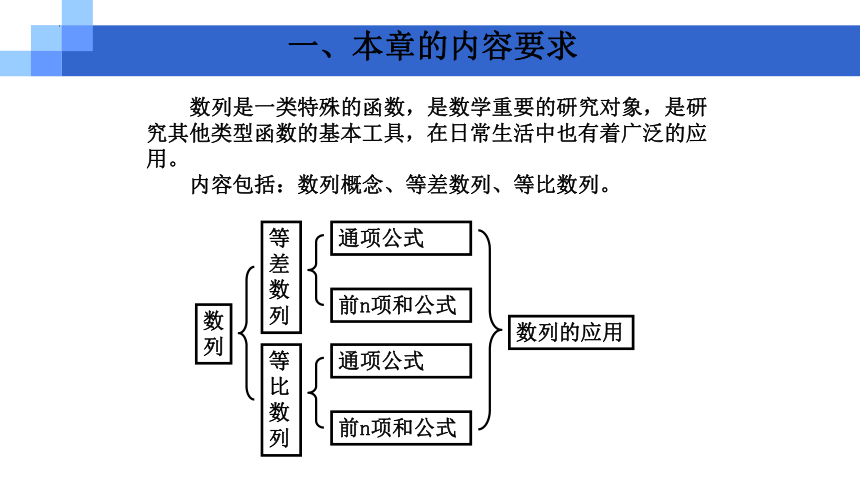 | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 22:17:06 | ||
图片预览









文档简介
(共20张PPT)
一、本章的内容要求
数列是一类特殊的函数,是数学重要的研究对象,是研究其他类型函数的基本工具,在日常生活中也有着广泛的应用。
内容包括:数列概念、等差数列、等比数列。
数列
等比数列
等差数列
前n项和公式
通项公式
前n项和公式
通项公式
数列的应用
(1)数列概念
通过日常生活和数学中的实例,了解数列的概念和表示方法(列表、图象、通项公式),了解数列是一种特殊函数。
(2)等差数列
①通过生活中的实例,理解等差数列的概念和通项公式的意义。
②探索并掌握等差数列的前n项和公式,理解等差数列的通项公式与前n项和公式的关系。
③能在具体的问题情境中,发现数列的等差关系,并解决相应的问题。
④体会等差数列与一次函数的关系。
一、本章的内容要求
(3)等比数列
①通过生活中的实例,理解等比数列的概念和通项公式的意义。
②探索并掌握等比数列的前n项和公式,理解等比数列的通项公式与前n项和公式的关系。
③能在具体的问题情境中,发现数列的等比关系,并解决相应的问题。
④体会等比数列与指数函数的关系。
一、本章的内容要求
二、本章的学业要求
能够结合具体实例,理解通项公式对于数列的重要性,知道通项公式是这类函数的解析表达式;通过等差数列和等比数列的研究,感悟数列是可以用来刻画现实世界中一类具有递推规律事物的数学模型,掌握通项公式与前n项和公式的关系;能运用数列解决简单的实际问题。
重点提升数学抽象、数学运算、直观想象、数学建模和逻辑推理素养。
三、考点聚焦突破
考点一 等差(等比)数列基本量的运算
解:设数列{an}首项为a1,公比为q(q≠1),
三、考点聚焦突破
考点二 等差(等比)数列的判定与证明
三、考点聚焦突破
【规律方法】
1.证明数列是等差数列的主要方法
(1)定义法:对于n≥2的任意正整数,验证an-an-1为常数.
(2)等差中项法:验证2an-1=an+an-2(n≥3,n∈N+)都成立.
2.判定一个数列是等差数列还常用到的结论
(1)通项公式:an=pn+q(p,q为常数) {an}是等差数列.
(2)前n项和公式:Sn=An2+Bn(A,B为常数) {an}是等差数列.
问题的最终判定还是利用定义.
等比数列的判定与证明与等差数列的判定与证明方法相同。
三、考点聚焦突破
考点三 求数列的通项公式
三、考点聚焦突破
所以a2-a1=ln 2-ln 1,
a3-a2=ln 3-ln 2,
a4-a3=ln 4-ln 3,
………
an-an-1=ln n-ln(n-1)(n≥2).
把以上各式分别相加得an-a1=ln n-ln 1,
则an=2+ln n,且a1=2也适合,
因此an=2+ln n(n∈N+).
三、考点聚焦突破
(2)由an+1=2an+3,得an+1+3=2(an+3).
所以{bn}是以4为首项,2为公比的等比数列.
∴bn=4·2n-1=2n+1,∴an=2n+1-3.
三、考点聚焦突破
(3)由log2(Sn+1)=n+1,得Sn+1=2n+1,
当n=1时,a1=S1=3;
当n≥2时,an=Sn-Sn-1=2n,
三、考点聚焦突破
三、考点聚焦突破
三、考点聚焦突破
考点四 数列求和---分组转化法
【例4】已知在等比数列{an}中,a1=1,且a1,a2,a3-1成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=2n-1+an(n∈N+),求数列{bn}的前n项和为Sn.
解:(1)设等比数列{an}的公比为q,∵a1,a2,a3-1成等差数列,
∴an=a1qn-1=2n-1(n∈N+).
三、考点聚焦突破
(2)由(1)知bn=2n-1+an=2n-1+2n-1,
∴Sn=(1+1)+(3+2)+(5+22)+…+(2n-1+2n-1)
=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1)
∴Sn=n2+2n-1.
考点四 数列求和---裂项相消法
三、考点聚焦突破
即an+1=3an+2,又a2=8=3a1+2,
∴an+1=3an+2,n∈N+,∴an+1+1=3(an+1),
∴数列{an+1}是等比数列,且首项为a1+1=3,公比为3,
∴an+1=3×3n-1=3n,∴an=3n-1.
三、考点聚焦突破
考点四 数列求和---错位相减法
【例6】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
三、考点聚焦突破
解:(1)设{an}的公比为q,
又S2n+1=bnbn+1,bn+1≠0,所以bn=2n+1.
三、考点聚焦突破
【规律方法】
三、考点聚焦突破
一、本章的内容要求
数列是一类特殊的函数,是数学重要的研究对象,是研究其他类型函数的基本工具,在日常生活中也有着广泛的应用。
内容包括:数列概念、等差数列、等比数列。
数列
等比数列
等差数列
前n项和公式
通项公式
前n项和公式
通项公式
数列的应用
(1)数列概念
通过日常生活和数学中的实例,了解数列的概念和表示方法(列表、图象、通项公式),了解数列是一种特殊函数。
(2)等差数列
①通过生活中的实例,理解等差数列的概念和通项公式的意义。
②探索并掌握等差数列的前n项和公式,理解等差数列的通项公式与前n项和公式的关系。
③能在具体的问题情境中,发现数列的等差关系,并解决相应的问题。
④体会等差数列与一次函数的关系。
一、本章的内容要求
(3)等比数列
①通过生活中的实例,理解等比数列的概念和通项公式的意义。
②探索并掌握等比数列的前n项和公式,理解等比数列的通项公式与前n项和公式的关系。
③能在具体的问题情境中,发现数列的等比关系,并解决相应的问题。
④体会等比数列与指数函数的关系。
一、本章的内容要求
二、本章的学业要求
能够结合具体实例,理解通项公式对于数列的重要性,知道通项公式是这类函数的解析表达式;通过等差数列和等比数列的研究,感悟数列是可以用来刻画现实世界中一类具有递推规律事物的数学模型,掌握通项公式与前n项和公式的关系;能运用数列解决简单的实际问题。
重点提升数学抽象、数学运算、直观想象、数学建模和逻辑推理素养。
三、考点聚焦突破
考点一 等差(等比)数列基本量的运算
解:设数列{an}首项为a1,公比为q(q≠1),
三、考点聚焦突破
考点二 等差(等比)数列的判定与证明
三、考点聚焦突破
【规律方法】
1.证明数列是等差数列的主要方法
(1)定义法:对于n≥2的任意正整数,验证an-an-1为常数.
(2)等差中项法:验证2an-1=an+an-2(n≥3,n∈N+)都成立.
2.判定一个数列是等差数列还常用到的结论
(1)通项公式:an=pn+q(p,q为常数) {an}是等差数列.
(2)前n项和公式:Sn=An2+Bn(A,B为常数) {an}是等差数列.
问题的最终判定还是利用定义.
等比数列的判定与证明与等差数列的判定与证明方法相同。
三、考点聚焦突破
考点三 求数列的通项公式
三、考点聚焦突破
所以a2-a1=ln 2-ln 1,
a3-a2=ln 3-ln 2,
a4-a3=ln 4-ln 3,
………
an-an-1=ln n-ln(n-1)(n≥2).
把以上各式分别相加得an-a1=ln n-ln 1,
则an=2+ln n,且a1=2也适合,
因此an=2+ln n(n∈N+).
三、考点聚焦突破
(2)由an+1=2an+3,得an+1+3=2(an+3).
所以{bn}是以4为首项,2为公比的等比数列.
∴bn=4·2n-1=2n+1,∴an=2n+1-3.
三、考点聚焦突破
(3)由log2(Sn+1)=n+1,得Sn+1=2n+1,
当n=1时,a1=S1=3;
当n≥2时,an=Sn-Sn-1=2n,
三、考点聚焦突破
三、考点聚焦突破
三、考点聚焦突破
考点四 数列求和---分组转化法
【例4】已知在等比数列{an}中,a1=1,且a1,a2,a3-1成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=2n-1+an(n∈N+),求数列{bn}的前n项和为Sn.
解:(1)设等比数列{an}的公比为q,∵a1,a2,a3-1成等差数列,
∴an=a1qn-1=2n-1(n∈N+).
三、考点聚焦突破
(2)由(1)知bn=2n-1+an=2n-1+2n-1,
∴Sn=(1+1)+(3+2)+(5+22)+…+(2n-1+2n-1)
=[1+3+5+…+(2n-1)]+(1+2+22+…+2n-1)
∴Sn=n2+2n-1.
考点四 数列求和---裂项相消法
三、考点聚焦突破
即an+1=3an+2,又a2=8=3a1+2,
∴an+1=3an+2,n∈N+,∴an+1+1=3(an+1),
∴数列{an+1}是等比数列,且首项为a1+1=3,公比为3,
∴an+1=3×3n-1=3n,∴an=3n-1.
三、考点聚焦突破
考点四 数列求和---错位相减法
【例6】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
三、考点聚焦突破
解:(1)设{an}的公比为q,
又S2n+1=bnbn+1,bn+1≠0,所以bn=2n+1.
三、考点聚焦突破
【规律方法】
三、考点聚焦突破
