2023-2024学年数学苏科版九年级下册第6章图形的相似检测卷(含答案)
文档属性
| 名称 | 2023-2024学年数学苏科版九年级下册第6章图形的相似检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 457.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 12:34:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学苏科版九年级下册第6章图形的相似检测卷
一、选择题
1.如图,由图形M改变为图形N,这种图形改变属于( )
A.平移 B.轴对称 C.旋转 D.相似
2.如图,直线,,直线和被,,所截,,,,则DE的长为( )
A.3 B.4 C.5 D.6
3.如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A. B.
C.是的中点 D.
4.在平面直角坐标系中,三个顶点的坐标分别为,,.以原点O为位似中心,把这个三角形缩小为原来的,得到,则点A的对应点C的坐标是( )
A. B.
C. D.或
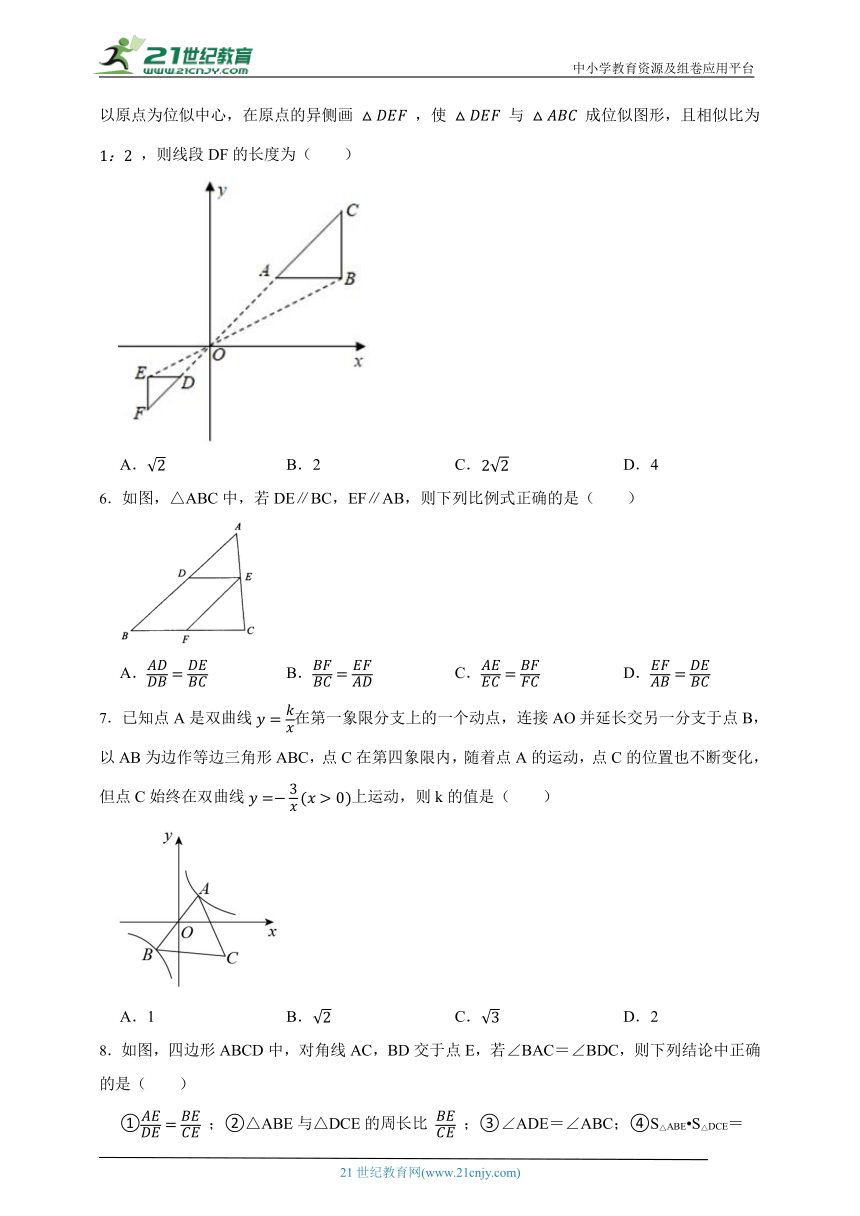
5.如图,在平面直角坐标系中, 的顶点坐标分别是 , , ,以原点为位似中心,在原点的异侧画 ,使 与 成位似图形,且相似比为 ,则线段DF的长度为( )
A. B.2 C. D.4
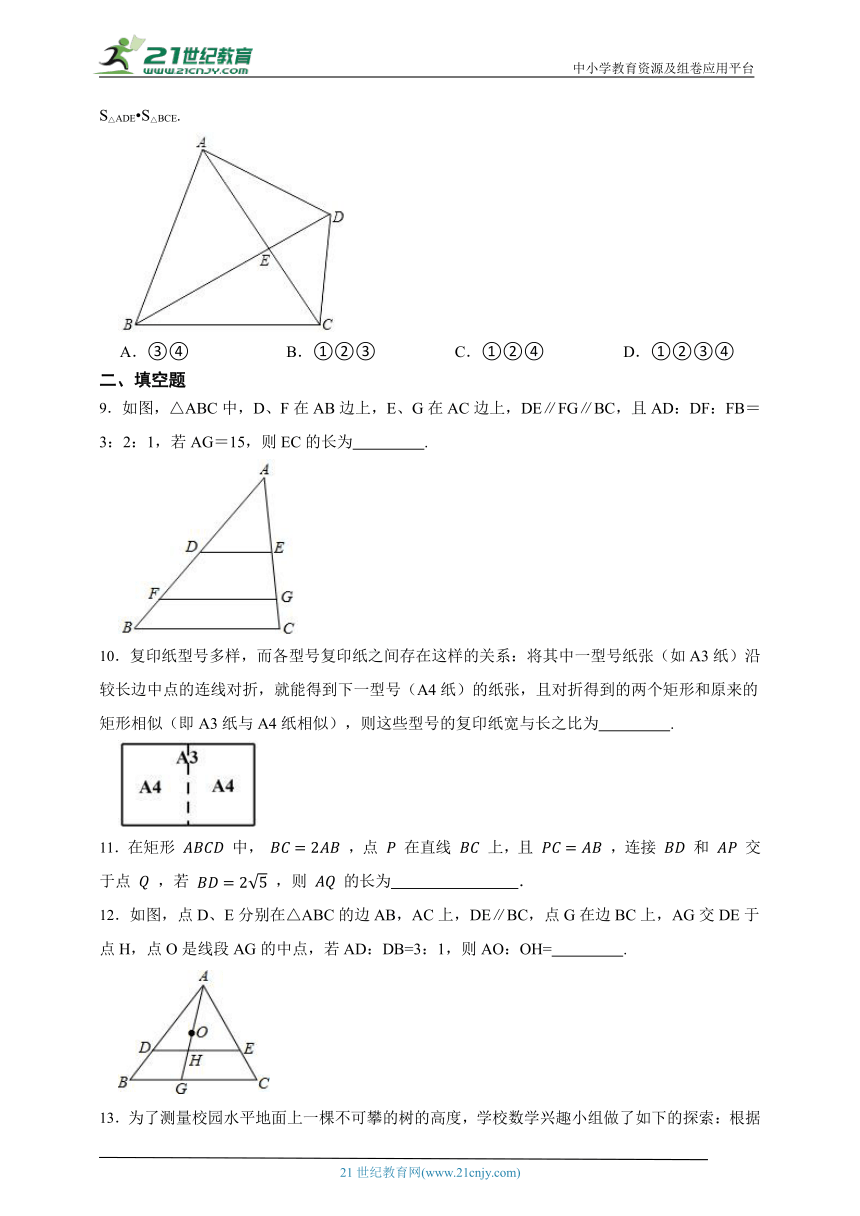
6.如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
7.已知点A是双曲线在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线上运动,则k的值是( )
A.1 B. C. D.2
8.如图,四边形ABCD中,对角线AC,BD交于点E,若∠BAC=∠BDC,则下列结论中正确的是( )
① ;②△ABE与△DCE的周长比 ;③∠ADE=∠ABC;④S△ABE S△DCE=S△ADE S△BCE.
A.③④ B.①②③ C.①②④ D.①②③④
二、填空题
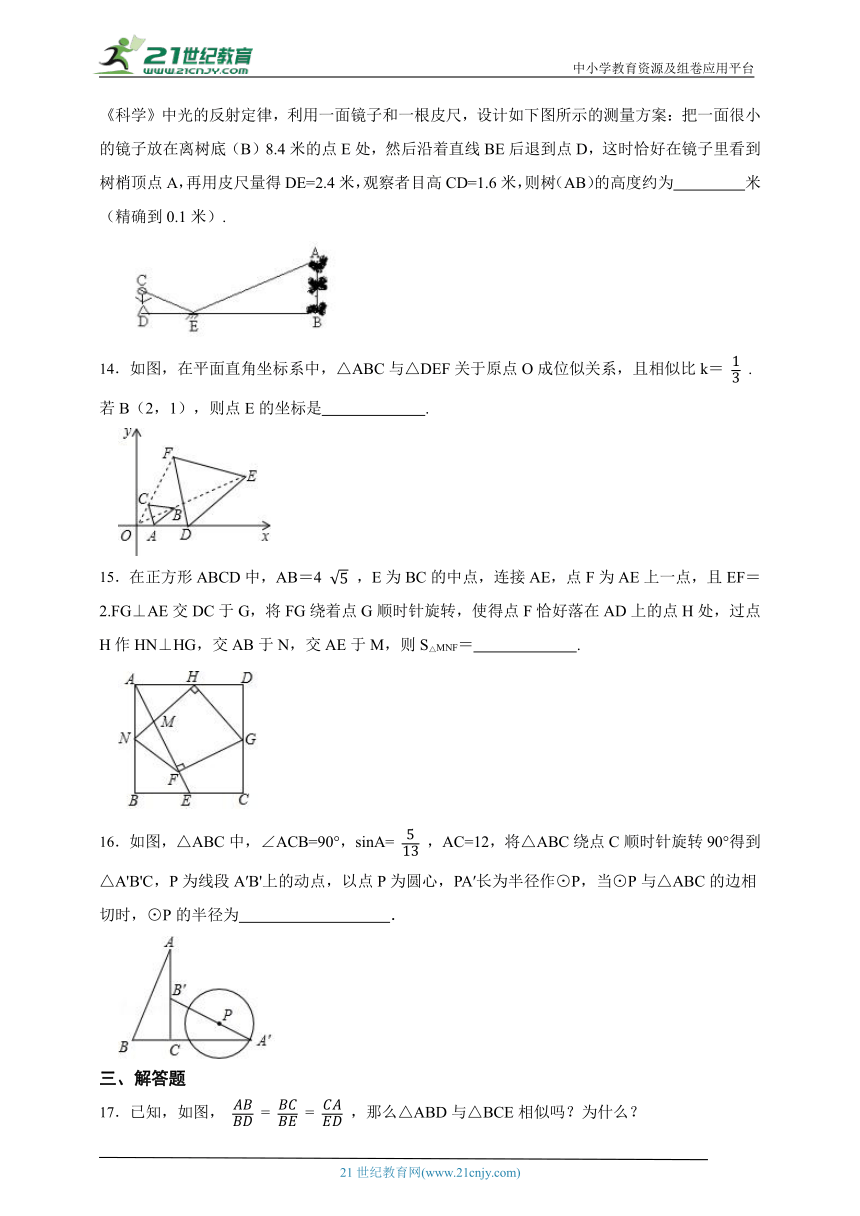
9.如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为 .
10.复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为 .
11.在矩形 中, ,点 在直线 上,且 ,连接 和 交于点 ,若 ,则 的长为 .
12.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
13.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为 米(精确到0.1米).
14.如图,在平面直角坐标系中,△ABC与△DEF关于原点O成位似关系,且相似比k= .若B(2,1),则点E的坐标是 .
15.在正方形ABCD中,AB=4 ,E为BC的中点,连接AE,点F为AE上一点,且EF=2.FG⊥AE交DC于G,将FG绕着点G顺时针旋转,使得点F恰好落在AD上的点H处,过点H作HN⊥HG,交AB于N,交AE于M,则S△MNF= .
16.如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
三、解答题
17.已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?
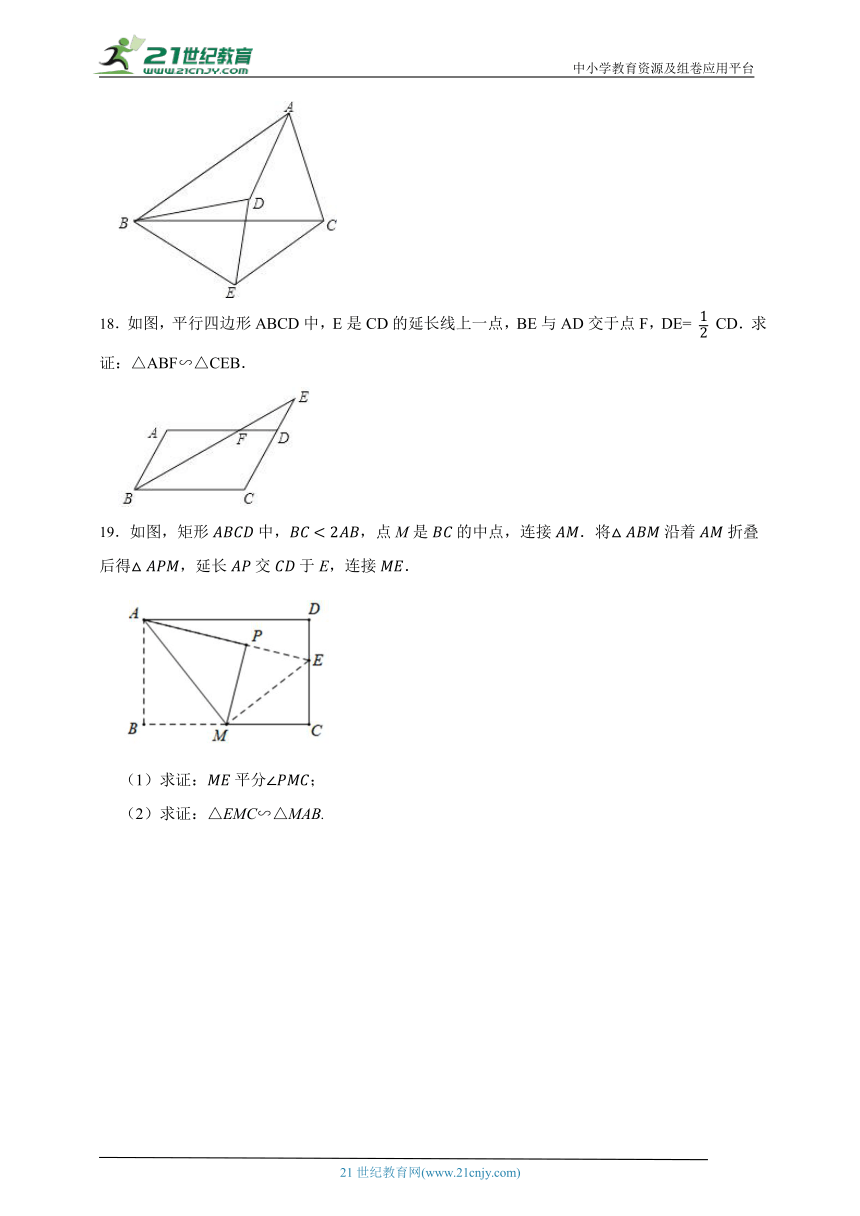
18.如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.求证:△ABF∽△CEB.
19.如图,矩形中,,点M是的中点,连接.将沿着折叠后得,延长交于E,连接.
(1)求证:平分;
(2)求证:△EMC∽△MAB.
20.如图,在锐角三角形ABC中,,是的外接圆,连结AO,BO,延长BO交AC于点D.
(1)求证:AO平分;
(2)若的半径为5,,求DC的长;
(3)若,求的值(用含m的代数式表示).
21.如图,在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,AB=2,则何时矩形PMCN的面积最大?最大面积是多少?
22.如图①,在矩形ABCD中,AB=4,AD=6,点E在边BC上,且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动.设点P的运动时间为t秒.(t>0)
(1)当点P和点B重合时,线段PQ的长为 ;
(2)当点Q和点D重合时,求的值;
(3)当点P在边AD上运动时,如图②,求证:为定值,并求这个值;
(4)作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD的重叠部分为轴对称四边形时,直接写出t的取值范围.
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】9
10.【答案】
11.【答案】 或
12.【答案】2:1
13.【答案】5.6
14.【答案】(6,3)
15.【答案】
16.【答案】 或
17.【答案】解:∵ = = ,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
∵ = ,
∴ = ,
∴△ABD∽△CBE
18.【答案】证明:
∵四边形ABCD是平行四边形
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB.
19.【答案】(1)证明:由折叠性质可得:,,
∴,
∴,
∵点M是BC的中点,
∴,
∵,
∴,
∴,
∴平分;
(2)证明:由折叠性质可得:,
由(1)得:,
∵,
∴,
∵,
∵,
∴,
∵,
∴
20.【答案】(1)证明:如图,过点O作于点M,作于点N.
,
,
∴OM=ON,
平分;
(2)解:由(1)可知,∠OAD=∠OAB,
,
∴∠OBA=∠OAB,
∴∠OAD=∠OBA,
∵∠ADO=∠BDA
∴,
,
解得,
∵,
∴,
,,
CD=1.5;
(3)解:延长BD交圆于点E,连接CE,设,
,
,,
∵∠ACE=∠ABO,
由(2)得,∠OAD=∠OBA,
∴∠ACE=∠DAO,
∴OA∥CE,
∴
21.【答案】解:设PA=x ,矩形PMCN的面积为y 则BP=AB﹣AP=2﹣x,
在直角△ABC中:∵AC=1 AB=2,
∴BC= ,
∵PM⊥BC,PN⊥AC,
∴PM‖AC,PN‖BC,
∴ , ,
∴ , ,
∴PM= ,PN= x,
∴y=PM×PN= × x= (2x﹣x2),
=﹣ (x﹣1)2+
∴当x=1时,即PA=1,P是AB的中点时矩形PMCN的面积最大,最大面积是
22.【答案】(1)2
(2)解:解:如图所示,
∵四边形ABCD是矩形,
∴∠PBE=∠ECD=90°,
∴∠1+∠2=90°,
∵∠PEQ=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∴△PBE∽△ECD,
∴
∵BE=2,CD=AB=4,
∴
∴的值为
(3)证明:作EF⊥AD于点F,如图:
∵∠A=∠B=∠AFE=90°,
∴四边形ABEF是矩形,
∴∠CEF=∠BEF=90°,FE=AB=4,
∵∠PEQ=90°=∠CEF,
∴∠PEF=∠QEC=90°﹣∠FEQ,
∵∠EFP=∠ECQ=90°,
∴△EFP∽△ECQ,
∴
∴的值为定值,这个值为1
(4)解: 0<t≤8﹣4或t=或t=8
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学苏科版九年级下册第6章图形的相似检测卷
一、选择题
1.如图,由图形M改变为图形N,这种图形改变属于( )
A.平移 B.轴对称 C.旋转 D.相似
2.如图,直线,,直线和被,,所截,,,,则DE的长为( )
A.3 B.4 C.5 D.6
3.如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A. B.
C.是的中点 D.
4.在平面直角坐标系中,三个顶点的坐标分别为,,.以原点O为位似中心,把这个三角形缩小为原来的,得到,则点A的对应点C的坐标是( )
A. B.
C. D.或
5.如图,在平面直角坐标系中, 的顶点坐标分别是 , , ,以原点为位似中心,在原点的异侧画 ,使 与 成位似图形,且相似比为 ,则线段DF的长度为( )
A. B.2 C. D.4
6.如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
7.已知点A是双曲线在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线上运动,则k的值是( )
A.1 B. C. D.2
8.如图,四边形ABCD中,对角线AC,BD交于点E,若∠BAC=∠BDC,则下列结论中正确的是( )
① ;②△ABE与△DCE的周长比 ;③∠ADE=∠ABC;④S△ABE S△DCE=S△ADE S△BCE.
A.③④ B.①②③ C.①②④ D.①②③④
二、填空题
9.如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为 .
10.复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为 .
11.在矩形 中, ,点 在直线 上,且 ,连接 和 交于点 ,若 ,则 的长为 .
12.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
13.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为 米(精确到0.1米).
14.如图,在平面直角坐标系中,△ABC与△DEF关于原点O成位似关系,且相似比k= .若B(2,1),则点E的坐标是 .
15.在正方形ABCD中,AB=4 ,E为BC的中点,连接AE,点F为AE上一点,且EF=2.FG⊥AE交DC于G,将FG绕着点G顺时针旋转,使得点F恰好落在AD上的点H处,过点H作HN⊥HG,交AB于N,交AE于M,则S△MNF= .
16.如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
三、解答题
17.已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?
18.如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.求证:△ABF∽△CEB.
19.如图,矩形中,,点M是的中点,连接.将沿着折叠后得,延长交于E,连接.
(1)求证:平分;
(2)求证:△EMC∽△MAB.
20.如图,在锐角三角形ABC中,,是的外接圆,连结AO,BO,延长BO交AC于点D.
(1)求证:AO平分;
(2)若的半径为5,,求DC的长;
(3)若,求的值(用含m的代数式表示).
21.如图,在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,AB=2,则何时矩形PMCN的面积最大?最大面积是多少?
22.如图①,在矩形ABCD中,AB=4,AD=6,点E在边BC上,且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动.设点P的运动时间为t秒.(t>0)
(1)当点P和点B重合时,线段PQ的长为 ;
(2)当点Q和点D重合时,求的值;
(3)当点P在边AD上运动时,如图②,求证:为定值,并求这个值;
(4)作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD的重叠部分为轴对称四边形时,直接写出t的取值范围.
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】9
10.【答案】
11.【答案】 或
12.【答案】2:1
13.【答案】5.6
14.【答案】(6,3)
15.【答案】
16.【答案】 或
17.【答案】解:∵ = = ,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
∵ = ,
∴ = ,
∴△ABD∽△CBE
18.【答案】证明:
∵四边形ABCD是平行四边形
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB.
19.【答案】(1)证明:由折叠性质可得:,,
∴,
∴,
∵点M是BC的中点,
∴,
∵,
∴,
∴,
∴平分;
(2)证明:由折叠性质可得:,
由(1)得:,
∵,
∴,
∵,
∵,
∴,
∵,
∴
20.【答案】(1)证明:如图,过点O作于点M,作于点N.
,
,
∴OM=ON,
平分;
(2)解:由(1)可知,∠OAD=∠OAB,
,
∴∠OBA=∠OAB,
∴∠OAD=∠OBA,
∵∠ADO=∠BDA
∴,
,
解得,
∵,
∴,
,,
CD=1.5;
(3)解:延长BD交圆于点E,连接CE,设,
,
,,
∵∠ACE=∠ABO,
由(2)得,∠OAD=∠OBA,
∴∠ACE=∠DAO,
∴OA∥CE,
∴
21.【答案】解:设PA=x ,矩形PMCN的面积为y 则BP=AB﹣AP=2﹣x,
在直角△ABC中:∵AC=1 AB=2,
∴BC= ,
∵PM⊥BC,PN⊥AC,
∴PM‖AC,PN‖BC,
∴ , ,
∴ , ,
∴PM= ,PN= x,
∴y=PM×PN= × x= (2x﹣x2),
=﹣ (x﹣1)2+
∴当x=1时,即PA=1,P是AB的中点时矩形PMCN的面积最大,最大面积是
22.【答案】(1)2
(2)解:解:如图所示,
∵四边形ABCD是矩形,
∴∠PBE=∠ECD=90°,
∴∠1+∠2=90°,
∵∠PEQ=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∴△PBE∽△ECD,
∴
∵BE=2,CD=AB=4,
∴
∴的值为
(3)证明:作EF⊥AD于点F,如图:
∵∠A=∠B=∠AFE=90°,
∴四边形ABEF是矩形,
∴∠CEF=∠BEF=90°,FE=AB=4,
∵∠PEQ=90°=∠CEF,
∴∠PEF=∠QEC=90°﹣∠FEQ,
∵∠EFP=∠ECQ=90°,
∴△EFP∽△ECQ,
∴
∴的值为定值,这个值为1
(4)解: 0<t≤8﹣4或t=或t=8
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
