2023-2024学年数学苏科版九年级下册第7章锐角三角函数检测卷(含答案)
文档属性
| 名称 | 2023-2024学年数学苏科版九年级下册第7章锐角三角函数检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 831.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 12:52:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学苏科版九年级下册第7章锐角三角函数检测卷
一、选择题
1.如图,某学习小组为测量学校A与河对岸凉亭B之间的距离,在学校附近选一点C,∠A=α,AC=4km.据此( )
A.4sinαkm B. C. D.4tanαkm
2.如图,在一个直角三角板ABC中,∠A=60°( )
A. B. C. D.
3.如图,在地面上的点A处测得树顶B的仰角为a,米,则树高为( )
A.米 B.米 C.米 D. 米
4.如图,一艘轮船航行至O点时,测得某灯塔A位于它的北偏东40°方向,且它与灯塔A相距13海里,继续沿正东方向航行,航行至点B处时,测得灯塔A恰好在它的正北方向,则的距离可表示为( )
A.海里 B.海里
C.海里 D.海里
5.如图,在等腰中,于点,则的值( )
A. B. C. D.
6.如图,在中,,,将绕点A逆时针旋转,得到,连接并延长交AB于点D,当时,的长是( )
A. B. C. D.
7.一个等边三角形的边长为2,则这个等边三角形的内切圆半径为( )
A. B.1 C. D.
8.如图所示,是我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为100,小正方形面积为4,则图中的正切值为( )
A. B. C. D.
二、填空题
9.已知中,,,,那么的长是 .
10.如图,是边长为6的等边三角形,点在边上,若,,则 .
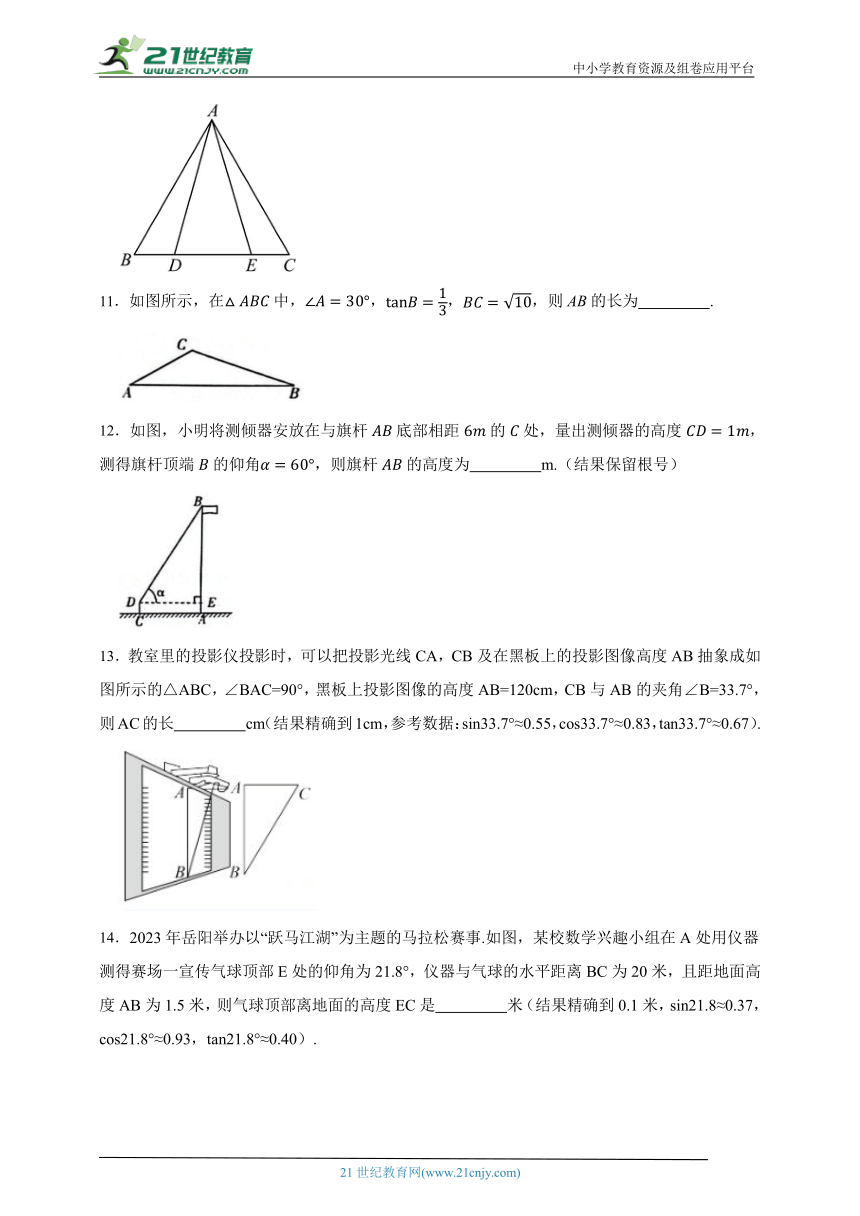
11.如图所示,在中,,,,则AB的长为 .
12.如图,小明将测倾器安放在与旗杆底部相距的处,量出测倾器的高度,测得旗杆顶端的仰角,则旗杆的高度为 m.(结果保留根号)
13.教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC,∠BAC=90°,黑板上投影图像的高度AB=120cm,CB与AB的夹角∠B=33.7°,则AC的长 cm(结果精确到1cm,参考数据:sin33.7°≈0.55,cos33.7°≈0.83,tan33.7°≈0.67).
14.2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在A处用仪器测得赛场一宣传气球顶部E处的仰角为21.8°,仪器与气球的水平距离BC为20米,且距地面高度AB为1.5米,则气球顶部离地面的高度EC是 米(结果精确到0.1米,sin21.8≈0.37,cos21.8°≈0.93,tan21.8°≈0.40).
15.在中,都是锐角,且,则是 三角形.
16.如图,在中,,分别以和为边向外作正方形和正方形,过点作的延长线的垂线,垂足为点.连接,交的延长线于点.下列说法:①;②若,,则;③;④;⑤若,,则的面积为,正确的有 .(填序号)
三、解答题
17.如图,为了测量旗杆的高度,在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
参考数据:,,
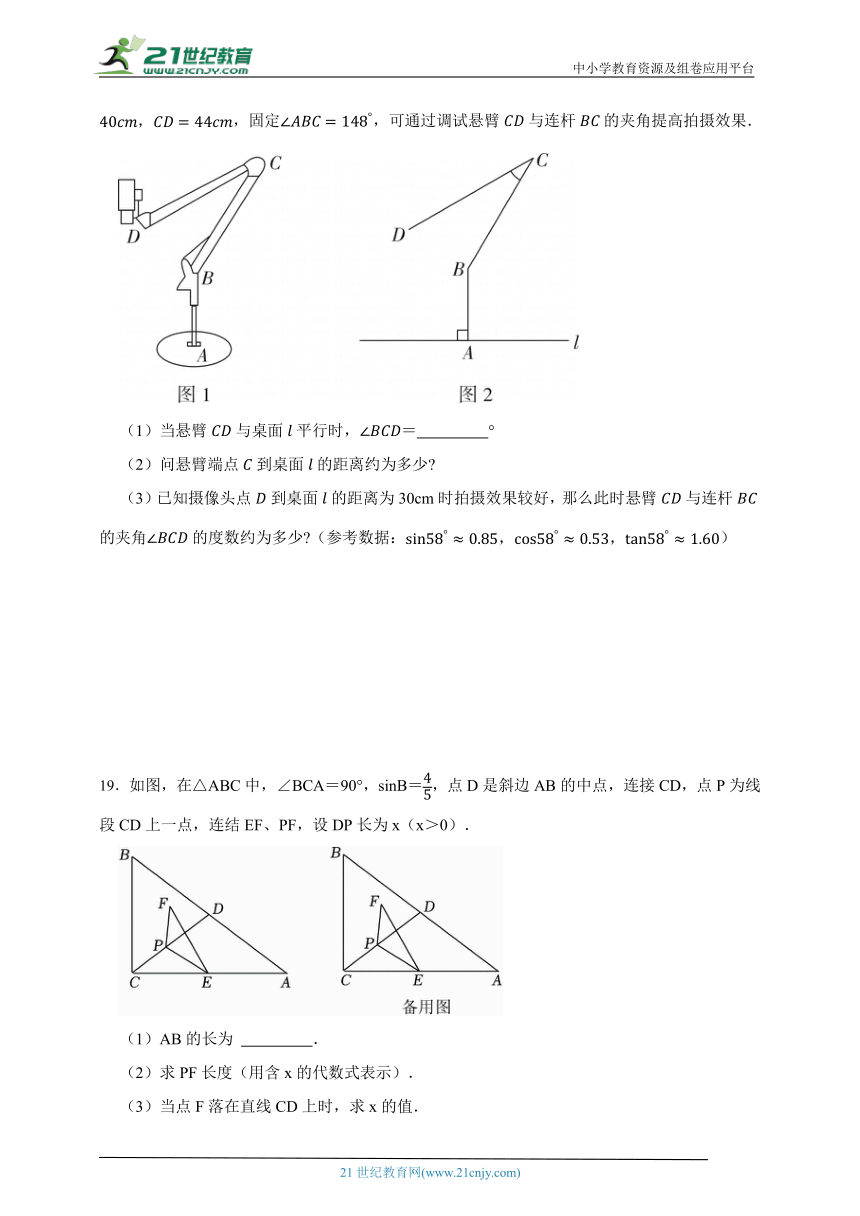
18.如图1,某款线上教学设备由底座,支撑臂,连杆,悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂,,固定,可通过调试悬臂与连杆的夹角提高拍摄效果.
(1)当悬臂与桌面平行时,= °
(2)问悬臂端点到桌面的距离约为多少
(3)已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少 (参考数据:)
19.如图,在△ABC中,∠BCA=90°,sinB=,点D是斜边AB的中点,连接CD,点P为线段CD上一点,连结EF、PF,设DP长为x(x>0).
(1)AB的长为 .
(2)求PF长度(用含x的代数式表示).
(3)当点F落在直线CD上时,求x的值.
(4)当直线PF与△ABC的边BC或AC垂直时,直接写出x的值.
20.如图,在矩形ABCD中,AC为对角线,,垂足为点E.
(1)求证:;
(2)若,,求的长.
21.如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点,连接交于点.
(1)求证:四边形是矩形;
(2)作射线交的延长线于点F,若,,求的长.
22.如图,在平面直角坐标系中,点在双曲线上,点B在双曲线上,且满足,连接.
(1)求双曲线的表达式;
(2)若,求的值.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】10
10.【答案】
11.【答案】
12.【答案】
13.【答案】80
14.【答案】9.5
15.【答案】等腰直角
16.【答案】①②③④
17.【答案】解:过点作交于,
则米,
在中,有米,
米
故BC米,
答:旗杆的高度约为米.
18.【答案】(1)58
(2)解:过作与交于,过作与交于
∴四边形为矩形
∴90°,
∵148°
∴58°
在中90°
∵∴
∴
(3)解:过作,,
∴
在中=90°
∴60°
∵58°∴32°
∴60°-32°=28°
19.【答案】(1)10
(2)解:∵点D是斜边AB的中点,AB=10,
∴CD=AB=4,
∵DP长为x,
∴CP=5﹣x,
∵作点C关于直线EP对称点F,
∴PF=PC=5﹣x;
(3)解:如图,当点F落在直线CD上时,
∵点E是边AC的中点,
∴CE=AC=4,
∵D为AB的中点,
∴CD=AD,
∴∠A=∠ECP,
∴cos∠A=cos∠ECP=,
∴,
∴x=;
(4)解: x=1或3
20.【答案】(1)证明:∵四边形是矩形,
∴.∴.
∵,∴.∴.
(2)解:在中,,设,,
则.
∵,
∴.
∵四边形是矩形,
∴.
在中,,.
∴.∴.
∴.∴.∴.
21.【答案】(1)证明:连接OC
∵AB为直径,C为上一点,
∴,∴,
∵点D为的中点,
∴,
∴,
∵,
∴,
∵DP是的切线,D为切点,
∴,
∴四边形是矩形.
(2)解:如图补全图形,
在中,,,
∴,,
∵,
∴,
在中,,,
∴,
∴,
在中,,,
∴,
∵矩形DECP对边平行,
∴,
∴,
∴.
22.【答案】(1)解:∵点在双曲线上,
∴,
∴.
(2)解:如图,分别过点A,B作x轴的垂线,垂足分别为C,D,如图所示:
则,
∴,,
∴,
∴,
∴,
∵A的坐标为,
∴,.
∵中,,
∴,
∴,.
∴B的坐标为,
∴将代入得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学苏科版九年级下册第7章锐角三角函数检测卷
一、选择题
1.如图,某学习小组为测量学校A与河对岸凉亭B之间的距离,在学校附近选一点C,∠A=α,AC=4km.据此( )
A.4sinαkm B. C. D.4tanαkm
2.如图,在一个直角三角板ABC中,∠A=60°( )
A. B. C. D.
3.如图,在地面上的点A处测得树顶B的仰角为a,米,则树高为( )
A.米 B.米 C.米 D. 米
4.如图,一艘轮船航行至O点时,测得某灯塔A位于它的北偏东40°方向,且它与灯塔A相距13海里,继续沿正东方向航行,航行至点B处时,测得灯塔A恰好在它的正北方向,则的距离可表示为( )
A.海里 B.海里
C.海里 D.海里
5.如图,在等腰中,于点,则的值( )
A. B. C. D.
6.如图,在中,,,将绕点A逆时针旋转,得到,连接并延长交AB于点D,当时,的长是( )
A. B. C. D.
7.一个等边三角形的边长为2,则这个等边三角形的内切圆半径为( )
A. B.1 C. D.
8.如图所示,是我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为100,小正方形面积为4,则图中的正切值为( )
A. B. C. D.
二、填空题
9.已知中,,,,那么的长是 .
10.如图,是边长为6的等边三角形,点在边上,若,,则 .
11.如图所示,在中,,,,则AB的长为 .
12.如图,小明将测倾器安放在与旗杆底部相距的处,量出测倾器的高度,测得旗杆顶端的仰角,则旗杆的高度为 m.(结果保留根号)
13.教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC,∠BAC=90°,黑板上投影图像的高度AB=120cm,CB与AB的夹角∠B=33.7°,则AC的长 cm(结果精确到1cm,参考数据:sin33.7°≈0.55,cos33.7°≈0.83,tan33.7°≈0.67).
14.2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在A处用仪器测得赛场一宣传气球顶部E处的仰角为21.8°,仪器与气球的水平距离BC为20米,且距地面高度AB为1.5米,则气球顶部离地面的高度EC是 米(结果精确到0.1米,sin21.8≈0.37,cos21.8°≈0.93,tan21.8°≈0.40).
15.在中,都是锐角,且,则是 三角形.
16.如图,在中,,分别以和为边向外作正方形和正方形,过点作的延长线的垂线,垂足为点.连接,交的延长线于点.下列说法:①;②若,,则;③;④;⑤若,,则的面积为,正确的有 .(填序号)
三、解答题
17.如图,为了测量旗杆的高度,在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
参考数据:,,
18.如图1,某款线上教学设备由底座,支撑臂,连杆,悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂,,固定,可通过调试悬臂与连杆的夹角提高拍摄效果.
(1)当悬臂与桌面平行时,= °
(2)问悬臂端点到桌面的距离约为多少
(3)已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少 (参考数据:)
19.如图,在△ABC中,∠BCA=90°,sinB=,点D是斜边AB的中点,连接CD,点P为线段CD上一点,连结EF、PF,设DP长为x(x>0).
(1)AB的长为 .
(2)求PF长度(用含x的代数式表示).
(3)当点F落在直线CD上时,求x的值.
(4)当直线PF与△ABC的边BC或AC垂直时,直接写出x的值.
20.如图,在矩形ABCD中,AC为对角线,,垂足为点E.
(1)求证:;
(2)若,,求的长.
21.如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点,连接交于点.
(1)求证:四边形是矩形;
(2)作射线交的延长线于点F,若,,求的长.
22.如图,在平面直角坐标系中,点在双曲线上,点B在双曲线上,且满足,连接.
(1)求双曲线的表达式;
(2)若,求的值.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】10
10.【答案】
11.【答案】
12.【答案】
13.【答案】80
14.【答案】9.5
15.【答案】等腰直角
16.【答案】①②③④
17.【答案】解:过点作交于,
则米,
在中,有米,
米
故BC米,
答:旗杆的高度约为米.
18.【答案】(1)58
(2)解:过作与交于,过作与交于
∴四边形为矩形
∴90°,
∵148°
∴58°
在中90°
∵∴
∴
(3)解:过作,,
∴
在中=90°
∴60°
∵58°∴32°
∴60°-32°=28°
19.【答案】(1)10
(2)解:∵点D是斜边AB的中点,AB=10,
∴CD=AB=4,
∵DP长为x,
∴CP=5﹣x,
∵作点C关于直线EP对称点F,
∴PF=PC=5﹣x;
(3)解:如图,当点F落在直线CD上时,
∵点E是边AC的中点,
∴CE=AC=4,
∵D为AB的中点,
∴CD=AD,
∴∠A=∠ECP,
∴cos∠A=cos∠ECP=,
∴,
∴x=;
(4)解: x=1或3
20.【答案】(1)证明:∵四边形是矩形,
∴.∴.
∵,∴.∴.
(2)解:在中,,设,,
则.
∵,
∴.
∵四边形是矩形,
∴.
在中,,.
∴.∴.
∴.∴.∴.
21.【答案】(1)证明:连接OC
∵AB为直径,C为上一点,
∴,∴,
∵点D为的中点,
∴,
∴,
∵,
∴,
∵DP是的切线,D为切点,
∴,
∴四边形是矩形.
(2)解:如图补全图形,
在中,,,
∴,,
∵,
∴,
在中,,,
∴,
∴,
在中,,,
∴,
∵矩形DECP对边平行,
∴,
∴,
∴.
22.【答案】(1)解:∵点在双曲线上,
∴,
∴.
(2)解:如图,分别过点A,B作x轴的垂线,垂足分别为C,D,如图所示:
则,
∴,,
∴,
∴,
∴,
∵A的坐标为,
∴,.
∵中,,
∴,
∴,.
∴B的坐标为,
∴将代入得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
