2023-2024学年数学人教版七年级下册第五章相交线与平行线常考易错检测卷(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版七年级下册第五章相交线与平行线常考易错检测卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 966.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学人教版七年级下册第五章相交线与平行线常考易错检测卷
一、选择题
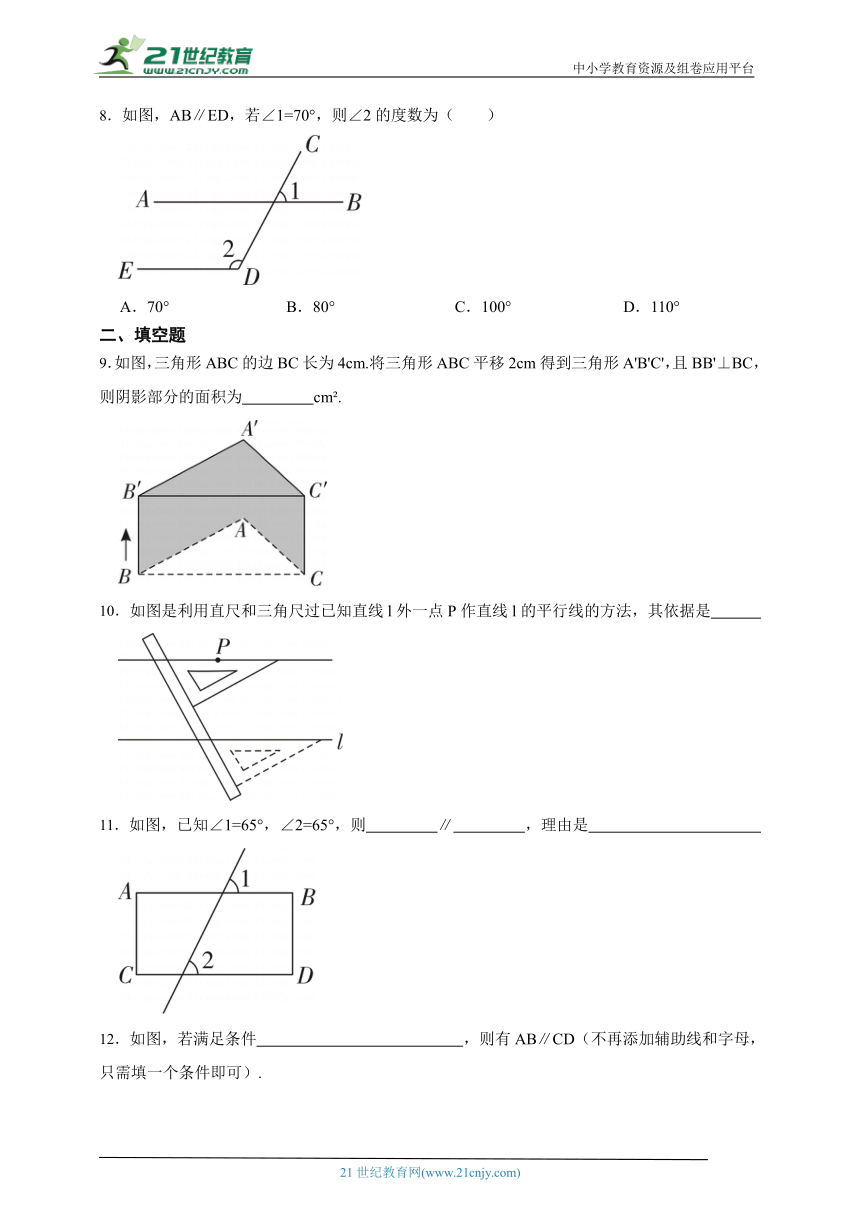
1.如图,将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形,至少需要移动 ( )
A.12格 B.11格 C.9 格 D.8格
2.在下列四边形中,AB不平行于 CD的是( )
A. B.
C. D.
3.下列图形中,根据∠1=∠2,能得到 AB∥CD 的是( )
A. B.
C. D.
4.如图,下列条件中,能判定a∥b的是( )
A.∠1+∠4=180° B.∠2=∠4
C.∠1=∠4 D.∠5=∠2+∠3
5.如图,AB∥EF,FD平分∠EFC.若∠DFC=50°,则∠ABC的度数为( )
A.50° B.60° C.100° D.120°
6.如图,直线a,b被直线c所截,且a∥b.若∠1=60°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
7.如图,将三角尺的直角顶点放在直尺的一边上.若∠1=75°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
8.如图,AB∥ED,若∠1=70°,则∠2的度数为( )
A.70° B.80° C.100° D.110°
二、填空题
9.如图,三角形ABC的边BC长为4cm.将三角形ABC平移2cm得到三角形A'B'C',且BB'⊥BC,则阴影部分的面积为 cm .
10.如图是利用直尺和三角尺过已知直线l外一点P作直线l的平行线的方法,其依据是
11.如图,已知∠1=65°,∠2=65°,则 ∥ ,理由是
12.如图,若满足条件 ,则有AB∥CD(不再添加辅助线和字母,只需填一个条件即可).
13.如图,∠A=70°,O是AB上一点,直线OD与AB 的夹角∠BOD=82°,要使 OD∥AC,直线 OD 应绕点O逆时针旋转至少 °.
14.如图所示,在三角形ABC中,BC=6cm.将三角形ABC以每秒2 cm的速度沿BC所在直线向右平移,所得图形对应为三角形DEF,设平移时间为t秒,若要使AD=2CE成立,则t的值为
15.一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 .(填序号)
16.已知a, b是在同一个平面内的两条直线,根据以下的条件写出a, b的位置关系:
(1)若a,b没有交点,则
(2)若a,b都平行于直线c,则
(3)若a,b有且仅有一个公共点,则
(4)若a∥c,b∥d,且直线c与直线d不平行,则
三、解答题
17.如图1,直线a,b所成的角跑到画板外面去了,有什么办法量出这两条直线所成的角的度数
(1)请在图2的画板上画出你的测量方案图,并做简要说明.
(2)写出该画法依据的定理:
18.完成下面的说理过程(填空).
如图,直线AB,CD被直线EF所截,∠1=∠2.判断AB与CD是否平行,并说明理由.
解:AB∥CD.理由如下:
∵∠2=∠3( ),∠1=∠2,
∴ ▲ = ▲ ,
∴ ▲ ∥ ▲ ( ).
19.如图,∠1=40°,∠2=55°,∠3=85°,直线l 与l 平行吗 为什么
20.如图,已知射线AB与直线CD相交于点O,OF平分∠BOC,OG⊥OF,AE∥OF,且∠A=30°.
(1)求∠DOF的度数.
(2)试说明:OD平分∠AOG.
21.如图,已知∠CFE+∠BDC=180°,∠DEF=∠B.
(1)试说明:AB∥EF.
(2)试判断∠AED与∠ACB的大小关系,并说明理由.
22.如图,已知AB∥CD,AE,CF分别平分∠BAC,∠DCG.试说明:AE∥CF.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】8
10.【答案】同位角相等,两直线平行
11.【答案】AB;CD;同位角相等,两直线平行
12.【答案】∠A=∠3(答案不唯一)
13.【答案】12
14.【答案】2或6
15.【答案】①③④
16.【答案】(1)a∥b
(2)a∥b
(3)a与b相交
(4)a与b相交
17.【答案】(1)解:如图:过点P作直线c∥a,测量出∠1的度数即可解决此题;
(2)两直线平行,同位角相等
18.【答案】解:AB∥CD,理由如下:
∵∠2=∠3(对顶角相等),∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥CD(同位角相等,两直线平行).
故答案为:对顶角相等;∠1,∠3;AB,CD;同位角相等,两直线平行.
19.【答案】解:l ∥l .理由如下:
∵∠2=55°(已知),∠2=∠4(对顶角相等),
∴∠4=55°(等量代换).
∵∠3=85°(已知),∠3+∠4+∠5=180°(平角定义),
∴∠5=40°,
又∵∠1=40°(已知),
∴∠1=∠5(等量代换),
∴l1∥l2(同位角相等、两直线平行).
20.【答案】(1)解:150°
(2)略
21.【答案】(1)略
(2)解:∠AED=∠ACB.理由略
22.【答案】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学人教版七年级下册第五章相交线与平行线常考易错检测卷
一、选择题
1.如图,将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形,至少需要移动 ( )
A.12格 B.11格 C.9 格 D.8格
2.在下列四边形中,AB不平行于 CD的是( )
A. B.
C. D.
3.下列图形中,根据∠1=∠2,能得到 AB∥CD 的是( )
A. B.
C. D.
4.如图,下列条件中,能判定a∥b的是( )
A.∠1+∠4=180° B.∠2=∠4
C.∠1=∠4 D.∠5=∠2+∠3
5.如图,AB∥EF,FD平分∠EFC.若∠DFC=50°,则∠ABC的度数为( )
A.50° B.60° C.100° D.120°
6.如图,直线a,b被直线c所截,且a∥b.若∠1=60°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
7.如图,将三角尺的直角顶点放在直尺的一边上.若∠1=75°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
8.如图,AB∥ED,若∠1=70°,则∠2的度数为( )
A.70° B.80° C.100° D.110°
二、填空题
9.如图,三角形ABC的边BC长为4cm.将三角形ABC平移2cm得到三角形A'B'C',且BB'⊥BC,则阴影部分的面积为 cm .
10.如图是利用直尺和三角尺过已知直线l外一点P作直线l的平行线的方法,其依据是
11.如图,已知∠1=65°,∠2=65°,则 ∥ ,理由是
12.如图,若满足条件 ,则有AB∥CD(不再添加辅助线和字母,只需填一个条件即可).
13.如图,∠A=70°,O是AB上一点,直线OD与AB 的夹角∠BOD=82°,要使 OD∥AC,直线 OD 应绕点O逆时针旋转至少 °.
14.如图所示,在三角形ABC中,BC=6cm.将三角形ABC以每秒2 cm的速度沿BC所在直线向右平移,所得图形对应为三角形DEF,设平移时间为t秒,若要使AD=2CE成立,则t的值为
15.一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 .(填序号)
16.已知a, b是在同一个平面内的两条直线,根据以下的条件写出a, b的位置关系:
(1)若a,b没有交点,则
(2)若a,b都平行于直线c,则
(3)若a,b有且仅有一个公共点,则
(4)若a∥c,b∥d,且直线c与直线d不平行,则
三、解答题
17.如图1,直线a,b所成的角跑到画板外面去了,有什么办法量出这两条直线所成的角的度数
(1)请在图2的画板上画出你的测量方案图,并做简要说明.
(2)写出该画法依据的定理:
18.完成下面的说理过程(填空).
如图,直线AB,CD被直线EF所截,∠1=∠2.判断AB与CD是否平行,并说明理由.
解:AB∥CD.理由如下:
∵∠2=∠3( ),∠1=∠2,
∴ ▲ = ▲ ,
∴ ▲ ∥ ▲ ( ).
19.如图,∠1=40°,∠2=55°,∠3=85°,直线l 与l 平行吗 为什么
20.如图,已知射线AB与直线CD相交于点O,OF平分∠BOC,OG⊥OF,AE∥OF,且∠A=30°.
(1)求∠DOF的度数.
(2)试说明:OD平分∠AOG.
21.如图,已知∠CFE+∠BDC=180°,∠DEF=∠B.
(1)试说明:AB∥EF.
(2)试判断∠AED与∠ACB的大小关系,并说明理由.
22.如图,已知AB∥CD,AE,CF分别平分∠BAC,∠DCG.试说明:AE∥CF.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】8
10.【答案】同位角相等,两直线平行
11.【答案】AB;CD;同位角相等,两直线平行
12.【答案】∠A=∠3(答案不唯一)
13.【答案】12
14.【答案】2或6
15.【答案】①③④
16.【答案】(1)a∥b
(2)a∥b
(3)a与b相交
(4)a与b相交
17.【答案】(1)解:如图:过点P作直线c∥a,测量出∠1的度数即可解决此题;
(2)两直线平行,同位角相等
18.【答案】解:AB∥CD,理由如下:
∵∠2=∠3(对顶角相等),∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥CD(同位角相等,两直线平行).
故答案为:对顶角相等;∠1,∠3;AB,CD;同位角相等,两直线平行.
19.【答案】解:l ∥l .理由如下:
∵∠2=55°(已知),∠2=∠4(对顶角相等),
∴∠4=55°(等量代换).
∵∠3=85°(已知),∠3+∠4+∠5=180°(平角定义),
∴∠5=40°,
又∵∠1=40°(已知),
∴∠1=∠5(等量代换),
∴l1∥l2(同位角相等、两直线平行).
20.【答案】(1)解:150°
(2)略
21.【答案】(1)略
(2)解:∠AED=∠ACB.理由略
22.【答案】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
