对数的运算
图片预览



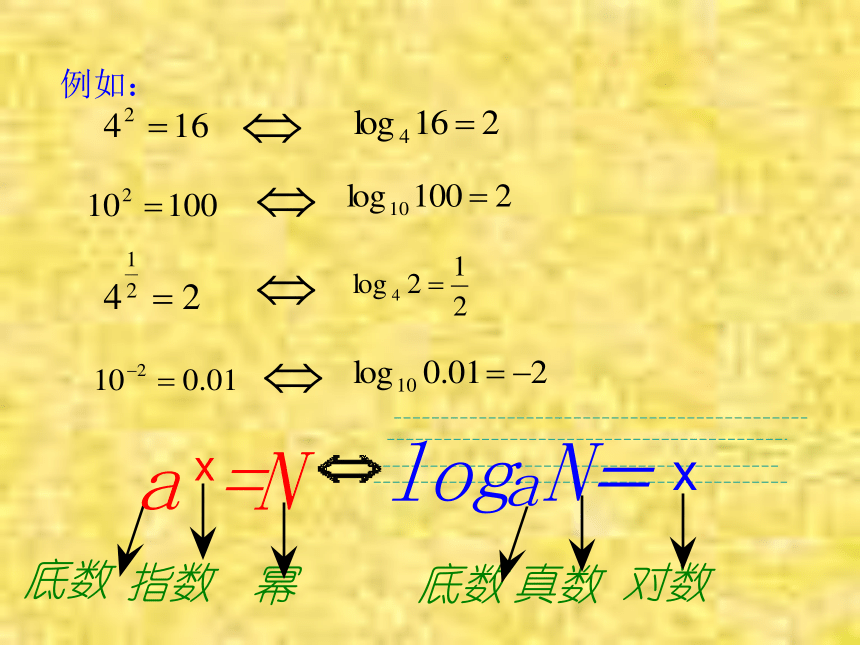




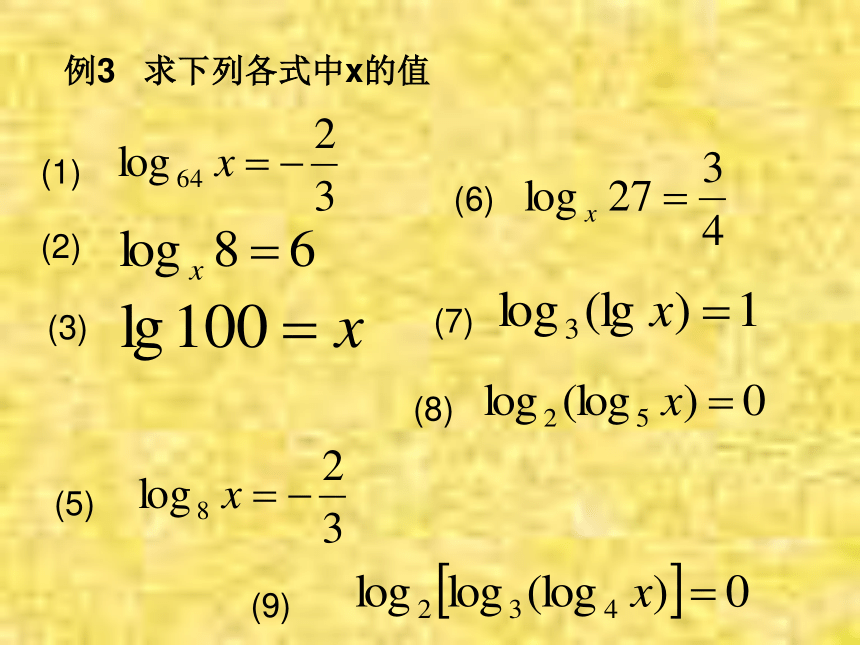
文档简介
课件29张PPT。对数的定义 函数关系:当x=20时 ,y≈16哪一年的人口数可达到18亿,19亿,20亿?a叫做对数的底数,N叫做真数。定义:记作例如: 相关性质: ⑴负数与零没有对数(∵在指数式中 N > 0 ) ⑵ ⑶对数恒等式例1求值⑷常用对数: 我们通常将以10为底的对数叫做常用对数。 为了简便,N的常用对数 简记作lgN。 ⑸自然对数: 在科学技术中常常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数。 为了简便,N的自然对数 简记作lnN。 (6)底数a的取值范围: 真数N的取值范围 :例2 将下列指数式化为对数式,对数式化为指数式(1)(2)(5)(4)(3)(6)例3 求下列各式中x的值(1)(2)(7)(6)(8)(5)(3)(9)判断下列各式是否正确(1)(3)(2)(4)(5) 用lgx,lgy,lgz表示下列各式:(1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz; 求下列各式的值(1)(4)(3)(2)化简下列各式(1)(2)(3)(4)(5)(6)(7)证明:①设 由对数的定义可以得: ∴MN= 即证得 证明:③设 由对数的定义可以得: ∴即证得 上述证明是运用转化的思想,先通过假设,将对数
式化成指数式,并利用幂的运算性质进行恒等变形;
然后再根据对数定义将指数式化成对数式。①简易语言表达:“积的对数 = 对数的和”……②有时逆向运用公式 ③真数的取值范围必须是 ④对公式容易错误记忆,要特别注意:其他重要公式1:证明:设 由对数的定义可以得: ∴即证得 其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式其他重要公式3:证明:由换底公式 取以b为底的对数得: 还可以变形,得 例1 计算(1) (2) 讲解范例 解 :=5+14=19解 :讲解范例 (3) 解 :=3例2 讲解范例 解(1) 解(2) 用 表示下列各式: (1) 例3计算: 讲解范例 解法一: 解法二: (2) 例3计算: 讲解范例 解: 练习 (1) (4) (3) (2) 1.求下列各式的值:证明:②设 由对数的定义可以得: ∴ 即证得 小结 :积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:其他重要公式:新授内容: 积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:为了证明以上公式,请同学们回顾一下指数运算法则 :课后作业:
式化成指数式,并利用幂的运算性质进行恒等变形;
然后再根据对数定义将指数式化成对数式。①简易语言表达:“积的对数 = 对数的和”……②有时逆向运用公式 ③真数的取值范围必须是 ④对公式容易错误记忆,要特别注意:其他重要公式1:证明:设 由对数的定义可以得: ∴即证得 其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式其他重要公式3:证明:由换底公式 取以b为底的对数得: 还可以变形,得 例1 计算(1) (2) 讲解范例 解 :=5+14=19解 :讲解范例 (3) 解 :=3例2 讲解范例 解(1) 解(2) 用 表示下列各式: (1) 例3计算: 讲解范例 解法一: 解法二: (2) 例3计算: 讲解范例 解: 练习 (1) (4) (3) (2) 1.求下列各式的值:证明:②设 由对数的定义可以得: ∴ 即证得 小结 :积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:其他重要公式:新授内容: 积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:为了证明以上公式,请同学们回顾一下指数运算法则 :课后作业:
