26.1.2 反比例函数与一次函数的综合应用课后同步作业(含答案)
文档属性
| 名称 | 26.1.2 反比例函数与一次函数的综合应用课后同步作业(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 796.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 20:27:29 | ||
图片预览


文档简介
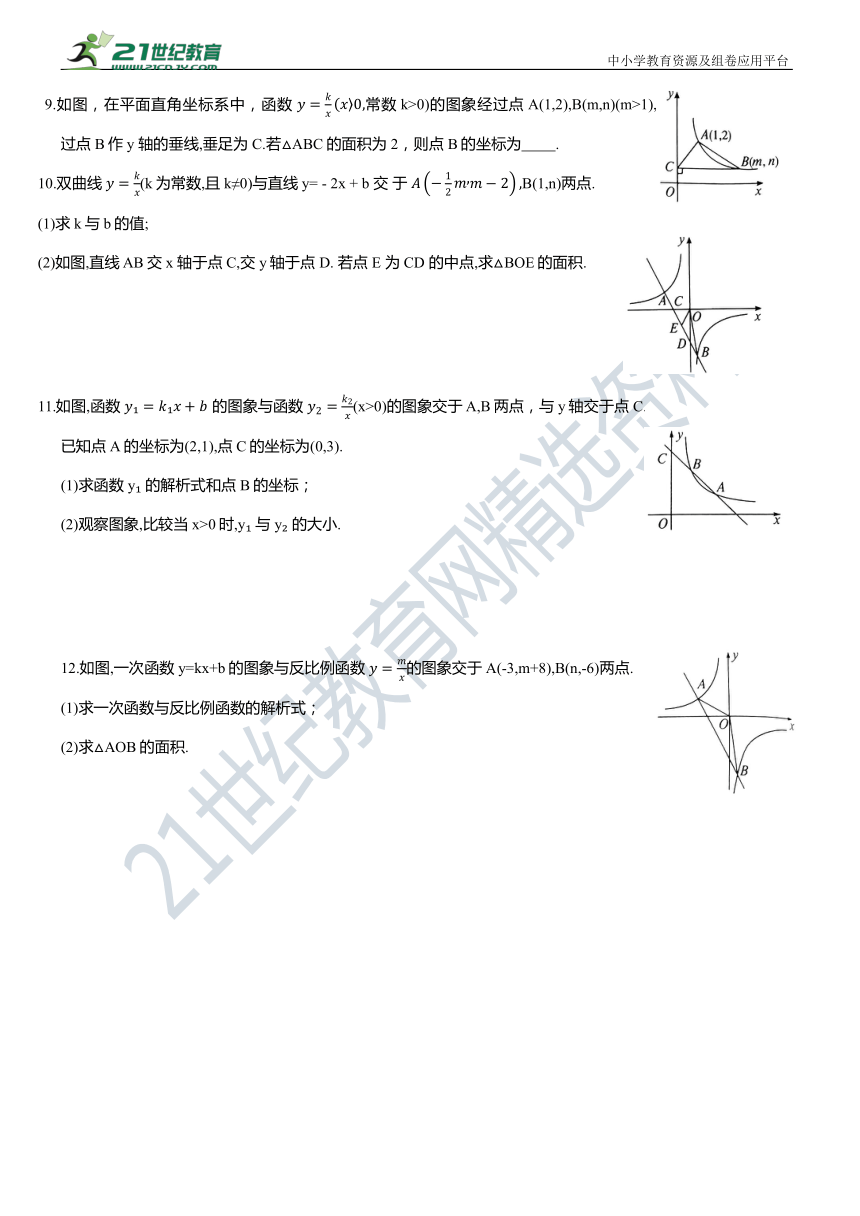
26.1.2反比例函数与一次函数的综合应用课后同步作业测评
1.下面给出的函数中,其图象是中心对称图形的是( )
①函数y=x;②函数. ③函数
A.①② B.②③ C.①③ D.都不是
2.如图,反比例函数 与正比例函数 的图象的一个交点是A(2,1).若 则x的取值范围在数轴上表示为( )
3.如图,等腰直角三角形 ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中点A 的横坐标为1,且两条直角边 AB,AC分别平行于x轴、y轴.若双曲线 (k≠0)与△ABC有交点,则 k的取值范围是( )
A.1C.1≤k≤4 D.1≤k<4
4.函数y=kx+k与 在同一平面直角坐标系中的图象为( )
5.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(-2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值时x的取值范围.
6.已知反比例函数 的图象与一次函数 的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的解析式;
(2)观察图象,当x>0时,直接写出 y >y 时自变量x的取值范围;
(3)如果点 C 与点 A 关于 x 轴对称,求△ABC的面积.
7.如图,直线 y=x+m与双曲线 相交于A,B两点.
(1)求m及k的值;
(2)不解关于 x,y的方程组 直接写出点 B的坐标;
(3)直线y=-2x+4m经过点 B 吗 请说明理由.
8.一次函数 和反比例函数 的图象如图所示,若y >y ,则x的取值范围是( )
A.-21
B. -2C. x<-2或x>1
D. x<-2或09.如图,在平面直角坐标系中,函数 常数k>0)的图象经过点A(1,2),B(m,n)(m>1),过点 B作y 轴的垂线,垂足为 C.若△ABC的面积为 2,则点B的坐标为 .
10.双曲线 (k为常数,且 k≠0)与直线y= - 2x + b 交 于 B(1,n)两点.
(1)求k与b的值;
中小学教育资源及组卷应用平台
(2)如图,直线 AB交x 轴于点C,交 y轴于点 D. 若点 E 为 CD 的中点,求△BOE的面积.
11.如图,函数 的图象与函数 (x>0)的图象交于 A,B两点,与y轴交于点C.已知点A的坐标为(2,1),点C的坐标为(0,3).
(1)求函数 y 的解析式和点 B的坐标;
(2)观察图象,比较当x>0时,y 与 y 的大小.
12.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(-3,m+8),B(n,-6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
1. C
2. D 由题图可知,若 ,则x的取值范围是x>2,故选 D.
3. C 由题意可得直线 y=x 与线段 BC 的交点坐标为(2,2),故 1≤k≤4.
4. D 若k>0,则双曲线 位于第一、三象限,直线y=kx+k经过第一、二、三象限;若k<0,则双曲线 位于第二、四象限,直线 y=kx+k经过第二、三、四象限.综上,选项 D中图象符合k<0的情况.
5.解(1)把点A(一2,1)的坐标代入 得m=-2,所以反比例函数的解析式为
把点 B(1,n)的坐标代入 得·n= -2,所以点B的坐标为(1,—2).
把点A(-2,1),B(1,-2)的坐标分别代入y=kx+b,得 解得
所以一次函数的解析式为 y=-x-1.
(2)当x<-2或06.解(1)因为函数 的图象经过点A(1,4),即 所以k=4,即
因为点B(m,-2)在 的图象上,所以m=-2,即点B的坐标为(-2,-2).
又一次函数 的图象过A,B 两点,
即 解得
所以
综上,可得
(2)当x>0时,要使 y >y ,即反比例函数的图象总在一次函数的图象上方,所以0(3)因为点C与点A关于x轴对称,所以C(1,一4).
过点B作BD⊥AC,垂足为 D,则D(1,-2),
于是△ABC的高BD=1-(-2)=3,底AC=4-(-4)=8.
所以
7.解(1)把点A(2,1)的坐标分别代入直线 y=x+m与双曲线 的解析式,得m=-1,k=2.
(2)点B的坐标为(-1,-2).
(3)把x=-1,m=-1 代入y=-2x+4m,得y=-2×(-1)+4×(-1)=2-4=-2,所以直线y=-2x+4m经过点B(-1,-2).
8. D 由题图可知,若. ,则 x 的取值范围是x<—2 或09.(3, ) ∵函数 常数k>0)的图象经过点A(1,2),∴k=2.
又点B(m,n)在该函数图象上,
在△ABC 中,BC=m,边BC上的高为
解得
∴点B的坐标为(3, )
10.解(1)∵点 B(1,n),在直线 y=—2x+b上,
解得 将点B的坐标代入反比例函数 则 解得k=-4.
(2)由(1)得直线 AB的解析式为y=-2x-2.令x=0,解得y=-2;令y=0,解得x=-1.∴C(-1,0),D(0,-2).
∵点E为CD的中点,∴点
11.解(1)由题意,得 解得
所以
又点A在函数 的图象上,
所以 解得 所以
解方程组
所以点B的坐标为(1,2).
(2)当x=1或x=2时,
当1当02时,y 12.解(1)把点A(-3,m+8)的坐标代入 得m+
∴m=-6.∴反比例函数的解析式为
把 B(n,-6)代入 得
∴n=1. ∴点A(-3,2),B(1,-6).
把A,B两点的坐标代入y=kx+b,
得 解得
∴一次函数的解析式为y=-2x-4.
(2)如图,过点 A 作AD⊥x 轴,垂足为点 D,过点B作BE⊥x轴,垂足为点 E.
∵直线 AB 对应的函 数 解 析 式 为 y =—2x—4,∴直线AB与x轴的交点C(-2,0).
∴OC=2.
∵A(-3,2),B(1,-6),∴AD=2,BE=6.
1.下面给出的函数中,其图象是中心对称图形的是( )
①函数y=x;②函数. ③函数
A.①② B.②③ C.①③ D.都不是
2.如图,反比例函数 与正比例函数 的图象的一个交点是A(2,1).若 则x的取值范围在数轴上表示为( )
3.如图,等腰直角三角形 ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中点A 的横坐标为1,且两条直角边 AB,AC分别平行于x轴、y轴.若双曲线 (k≠0)与△ABC有交点,则 k的取值范围是( )
A.1
4.函数y=kx+k与 在同一平面直角坐标系中的图象为( )
5.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(-2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值时x的取值范围.
6.已知反比例函数 的图象与一次函数 的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的解析式;
(2)观察图象,当x>0时,直接写出 y >y 时自变量x的取值范围;
(3)如果点 C 与点 A 关于 x 轴对称,求△ABC的面积.
7.如图,直线 y=x+m与双曲线 相交于A,B两点.
(1)求m及k的值;
(2)不解关于 x,y的方程组 直接写出点 B的坐标;
(3)直线y=-2x+4m经过点 B 吗 请说明理由.
8.一次函数 和反比例函数 的图象如图所示,若y >y ,则x的取值范围是( )
A.-2
B. -2
D. x<-2或0
10.双曲线 (k为常数,且 k≠0)与直线y= - 2x + b 交 于 B(1,n)两点.
(1)求k与b的值;
中小学教育资源及组卷应用平台
(2)如图,直线 AB交x 轴于点C,交 y轴于点 D. 若点 E 为 CD 的中点,求△BOE的面积.
11.如图,函数 的图象与函数 (x>0)的图象交于 A,B两点,与y轴交于点C.已知点A的坐标为(2,1),点C的坐标为(0,3).
(1)求函数 y 的解析式和点 B的坐标;
(2)观察图象,比较当x>0时,y 与 y 的大小.
12.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(-3,m+8),B(n,-6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
1. C
2. D 由题图可知,若 ,则x的取值范围是x>2,故选 D.
3. C 由题意可得直线 y=x 与线段 BC 的交点坐标为(2,2),故 1≤k≤4.
4. D 若k>0,则双曲线 位于第一、三象限,直线y=kx+k经过第一、二、三象限;若k<0,则双曲线 位于第二、四象限,直线 y=kx+k经过第二、三、四象限.综上,选项 D中图象符合k<0的情况.
5.解(1)把点A(一2,1)的坐标代入 得m=-2,所以反比例函数的解析式为
把点 B(1,n)的坐标代入 得·n= -2,所以点B的坐标为(1,—2).
把点A(-2,1),B(1,-2)的坐标分别代入y=kx+b,得 解得
所以一次函数的解析式为 y=-x-1.
(2)当x<-2或0
因为点B(m,-2)在 的图象上,所以m=-2,即点B的坐标为(-2,-2).
又一次函数 的图象过A,B 两点,
即 解得
所以
综上,可得
(2)当x>0时,要使 y >y ,即反比例函数的图象总在一次函数的图象上方,所以0
过点B作BD⊥AC,垂足为 D,则D(1,-2),
于是△ABC的高BD=1-(-2)=3,底AC=4-(-4)=8.
所以
7.解(1)把点A(2,1)的坐标分别代入直线 y=x+m与双曲线 的解析式,得m=-1,k=2.
(2)点B的坐标为(-1,-2).
(3)把x=-1,m=-1 代入y=-2x+4m,得y=-2×(-1)+4×(-1)=2-4=-2,所以直线y=-2x+4m经过点B(-1,-2).
8. D 由题图可知,若. ,则 x 的取值范围是x<—2 或0
又点B(m,n)在该函数图象上,
在△ABC 中,BC=m,边BC上的高为
解得
∴点B的坐标为(3, )
10.解(1)∵点 B(1,n),在直线 y=—2x+b上,
解得 将点B的坐标代入反比例函数 则 解得k=-4.
(2)由(1)得直线 AB的解析式为y=-2x-2.令x=0,解得y=-2;令y=0,解得x=-1.∴C(-1,0),D(0,-2).
∵点E为CD的中点,∴点
11.解(1)由题意,得 解得
所以
又点A在函数 的图象上,
所以 解得 所以
解方程组
所以点B的坐标为(1,2).
(2)当x=1或x=2时,
当1
∴m=-6.∴反比例函数的解析式为
把 B(n,-6)代入 得
∴n=1. ∴点A(-3,2),B(1,-6).
把A,B两点的坐标代入y=kx+b,
得 解得
∴一次函数的解析式为y=-2x-4.
(2)如图,过点 A 作AD⊥x 轴,垂足为点 D,过点B作BE⊥x轴,垂足为点 E.
∵直线 AB 对应的函 数 解 析 式 为 y =—2x—4,∴直线AB与x轴的交点C(-2,0).
∴OC=2.
∵A(-3,2),B(1,-6),∴AD=2,BE=6.
