26.2 实际问题与反比例函数课后同步作业(含答案)
文档属性
| 名称 | 26.2 实际问题与反比例函数课后同步作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 766.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览



文档简介
实际问题与反比例函数课后同步作业测评
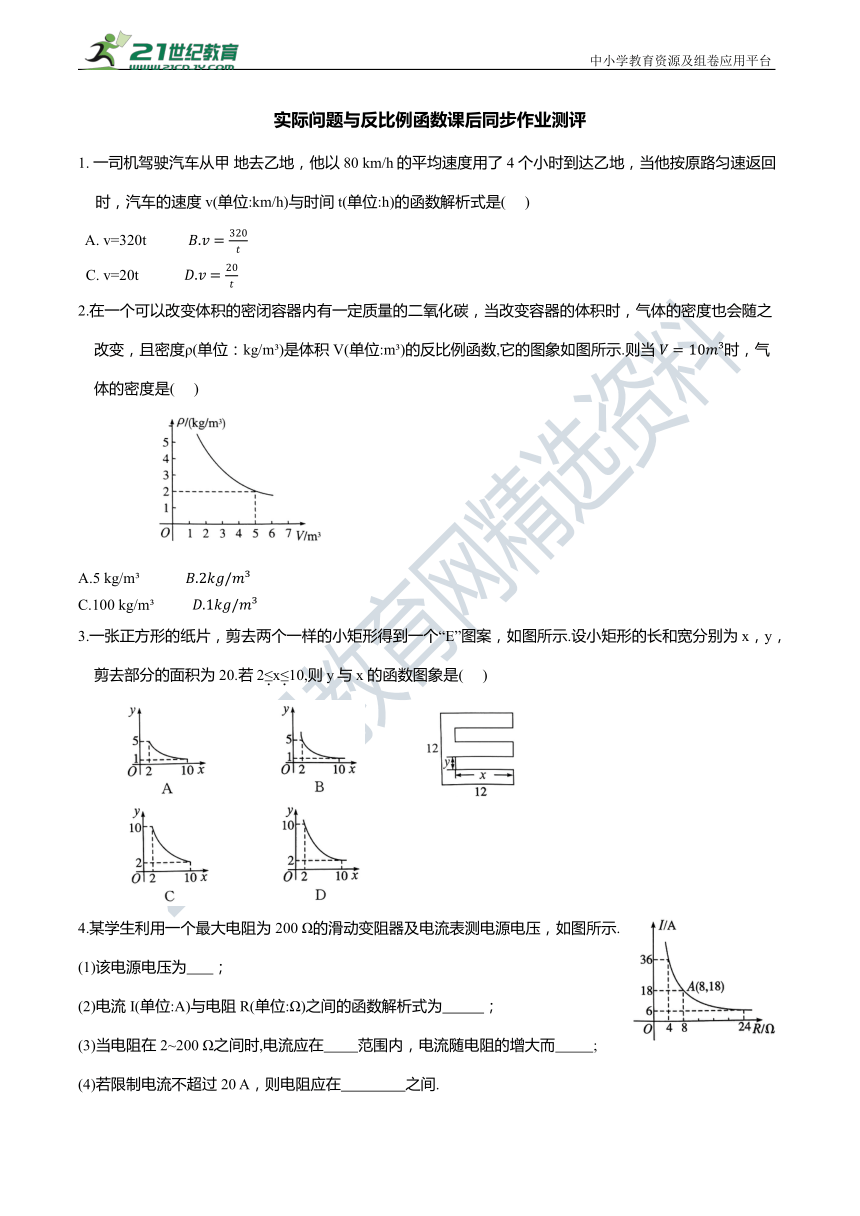
1. 一司机驾驶汽车从甲 地去乙地,他以80 km/h的平均速度用了 4 个小时到达乙地,当他按原路匀速返回时,汽车的速度v(单位:km/h)与时间 t(单位:h)的函数解析式是( )
A. v=320t
C. v=20t
2.在一个可以改变体积的密闭容器内有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,且密度ρ(单位:kg/m )是体积V(单位:m )的反比例函数,它的图象如图所示.则当 时,气体的密度是( )
A.5 kg/m
C.100 kg/m
3.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示.设小矩形的长和宽分别为x,y,剪去部分的面积为 20.若2≤x≤10,则y与x 的函数图象是( )
4.某学生利用一个最大电阻为 200 Ω的滑动变阻器及电流表测电源电压,如图所示.
(1)该电源电压为 ;
(2)电流 I(单位:A)与电阻R(单位:Ω)之间的函数解析式为 ;
(3)当电阻在 2~200 Ω之间时,电流应在 范围内,电流随电阻的增大而 ;
(4)若限制电流不超过 20 A,则电阻应在 之间.
5.已知一个长方体的体积是 100 cm ,它的长是 y cm,宽是 10 cm,高是 x cm.
(1)写出 y关于x 的函数解析式;
(2)当x=2时,求y的值.
6.你吃过拉面吗 实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度 y(单位:m)是面条的粗细(横截面积)S(单位:mm )的反比例函数,其图象如图所示.
(1)写出y关于S的函数解析式;
(2)当面条粗 1.6 mm 时,求面条的总长度是多少米.
中小学教育资源及组卷应用平台
7.某蓄水池的排水管每小时排水 8 m ,6 h 可将满池水排空.
(1)蓄水池的容积是多少
(2)如果增加排水管,使每小时的排水量达到Q(单位:m ),那么将满池水排空所需的时间t(单位:h)将如何变化
(3)写出t与Q的函数解析式;
(4)如果准备在 5 h 内将满池水排空,那么每小时的排水量至少为多少
(5)已知排水管的最大排水量为每小时 12 m ,那么最少多长时间可将满池水排空
8.教室里的饮水机接通电源就进入自动程序:开机加热时每分钟上升10℃,加热到100℃后停止加热,水温开始下降,此时水温(单位:℃)与开机后用时(单位:min)成反比例关系,直至水温降至 30 ℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为 30 ℃时,接通电源后,水温y(单位:℃)和时间x(单位:min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30
C.7:45 D.7:50
9.某地计划用120~180 天(含 120 与 180 天)的时间建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需时间 y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式,并给出自变量 x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多 5 000 立方米,工期比原计划减少了 24 天,原计划和实际平均每天运送土石方各是多少万立方米
10.蓄电池的电压为定值.使用此电源时,电流I(单位:A)与电阻R(单位:Ω)之间的函数关系如图所示.
(1)蓄电池的电压是多少 你能写出这一函数的解析式吗
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器,限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内
R/Ω 3 4 5 6 7 8 9 10
I/A 4
11.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度 y(单位:mg/mL)与服药时间x(单位:h)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y关于x的函数解析式;
(2)问血液中药物浓度不低于 4 mg/mL 的持续时间为多少小时
12.某厂从 2020年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年度 2020 2021 2022 2023
投入技改资金x/万元 2.5 3 4 4.5
产品成本y/(万元/件) 7.2 6 4.5 4
(1)请你认真分析表中数据,从你所学习过的一次函数、反比例函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其他函数的理由,并求出它的解析式;
(2)按照这种变化规律,若 2024 年已投入技改资金5万元.
①预计生产成本每件比2023年降低多少万元
②如果打算在2024年把每件产品成本降低到 3.2万元,则还需投入技改资金多少万元 (结果精确到 0.01万元)
1. B 由题意知 vt=80×4,则
2. D 3. A
4.(1)144 V (3)0.72~ 72A 减小
(4)7.2~200 Ω
5.解(1)由题意,得10xy=100,则
(2)当x=2时,
6.解(1)设反比例函数的解析式为
因为题中函数图象经过点(4,32),则有
所以k=128,即y与S 的函数解析式为 (S>0).
(2)当面条粗 S=1.6 mm 时,面条的总长度是
7.解(1)蓄水池的容积是(
(2)增加排水管会使时间缩短,将满池水排空所需的时间t会减少.
(3)因为容积V=48 m ,所以t 与Q的函数解析式为
即每小时的排水量至少为 9.6 m .
(5)设最少用 x h 将满池水排空,根据题意,得12x≥48,解得x≥4,即最少用4 h可将满池水排空.
8. A 由于开机加热时每分钟上升10℃,因此从30℃到100 ℃需要7 min. 设一次函数解析式 为 y= 将 ( 0 ,30),(7,100)代入 解得 k =10,b=30,所以y=10x+30(0≤x≤7).当y=50时,x=2.设反比例函数解析式为 将(7,100)代入 得k=700.当y=30 时, 所以 当y=50时,x=14,如图所示.所以饮水机的一个循环周期为 / min,每一个循环周期内,在0≤x≤2及 时间段内,水温不超过50℃,可直接饮用.
对于选项 A.7:20~8:45 之间有85 min, 3=15,即饮水机位于第 4 次重复开机后的第 15 min,此时水温不超过50℃,可直接饮用,符合题意.逐一分析,可知选项 B,C,D不符合题意,因此应选 A.
9.解(1)由题意,得 把、y=120代入 得x=3;把y=180代入 得x=2,所以自变量x的取值范围是2≤x≤3.故
(2)设原计划平均每天运送土石方 x万立方米,则实际平均每天运送土石方(x+0.5)万立方米.
由题意,得
方程两边同乘 x(x+0.5),得 360(x+0.5)一360x=24x(x+0.5).
化简得.x +0.5x-7.5=0,角解得
经检验, 均是原方程的根,但 不符合实际意义,故舍去.
又2≤x≤3,所以x=2.5 满足条件,即原计划平均每天运送土石方 2.5 万立方米,实际平均每天运送土石方3万立方米.
10.分析 从题图来看,I和R之间是反比例函数关系.电压U 就相当于反比例函数中的k.要写出函数的解析式,实际上就是确定 k(U),只需要一个条件即可,而题图中已给出了一个点的坐标,所以这个问题就解决了,填表实际上是已知自变量的值求函数值.
解(1)由题意,设函数解析式为
因为点A(9,4)在该函数图象上,所以U=IR=36(V),即蓄电池的电压是36 V.
所以所求函数解析式为
(2)表格中从左到右依次填:]12,9,7.2,6, ,4.5,3.6.
限制电流不超过10A,即Ⅰ最大为10A,代入关系式中得R=3.6Ω,为最小电阻,所以用电器的可变电阻应控制在R≥3.6 Ω 这个范围内.
11.解(1)当0≤x≤4时,设 y关于x 的函数解析式为 .将点(4,8)代入. 中,可得. 2,所以y=2x;
当4≤x≤10 时,设y关于x的函数解析式为 将点(4,8)代入 中,可得 32,所以 因此血液中药物浓度上升阶段的函数解析式为 y=2x(0≤x≤4),下降阶段的函数解析式为
(2)将y=4代入 y=2x中,得x=2;将y=4代入 中,得x=8,则血液中药物浓度不低于4 mg/mL 的持续时间为8-2=6(h).
12.解(1)若为一次函数,设其解析式为. 因为当x=2.5时,y=7.2;当x=3时,y=6,
所以 解得
所以一次函数的解析式为y=-2.4x+13.2.把x=4时,y=4.5代入此函数解析式,得左边≠右边.故不是一次函数.
若为反比例函数,设其解析式为 当x=2.5时,y=7.2,可得 得 所以反比例函数解析式为
验证:当x=3时, 符合反比例函数.
同理可验证:当 x=4 时,y=4. 5; 当 x=4. 5 时,y=4成立.故可用反比例函数 表示其变化规律.
(2)①当x=5时,
因为4—3.6=0.4(万元),所以预计生产成本每件比 2023 年降低 0.4 万元.
②当y=3.2时, 得x=5.625.
因为 5.625-5=0.625≈0.63(万元),
所以还需投入技改资金约0.63万元.
1. 一司机驾驶汽车从甲 地去乙地,他以80 km/h的平均速度用了 4 个小时到达乙地,当他按原路匀速返回时,汽车的速度v(单位:km/h)与时间 t(单位:h)的函数解析式是( )
A. v=320t
C. v=20t
2.在一个可以改变体积的密闭容器内有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,且密度ρ(单位:kg/m )是体积V(单位:m )的反比例函数,它的图象如图所示.则当 时,气体的密度是( )
A.5 kg/m
C.100 kg/m
3.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示.设小矩形的长和宽分别为x,y,剪去部分的面积为 20.若2≤x≤10,则y与x 的函数图象是( )
4.某学生利用一个最大电阻为 200 Ω的滑动变阻器及电流表测电源电压,如图所示.
(1)该电源电压为 ;
(2)电流 I(单位:A)与电阻R(单位:Ω)之间的函数解析式为 ;
(3)当电阻在 2~200 Ω之间时,电流应在 范围内,电流随电阻的增大而 ;
(4)若限制电流不超过 20 A,则电阻应在 之间.
5.已知一个长方体的体积是 100 cm ,它的长是 y cm,宽是 10 cm,高是 x cm.
(1)写出 y关于x 的函数解析式;
(2)当x=2时,求y的值.
6.你吃过拉面吗 实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度 y(单位:m)是面条的粗细(横截面积)S(单位:mm )的反比例函数,其图象如图所示.
(1)写出y关于S的函数解析式;
(2)当面条粗 1.6 mm 时,求面条的总长度是多少米.
中小学教育资源及组卷应用平台
7.某蓄水池的排水管每小时排水 8 m ,6 h 可将满池水排空.
(1)蓄水池的容积是多少
(2)如果增加排水管,使每小时的排水量达到Q(单位:m ),那么将满池水排空所需的时间t(单位:h)将如何变化
(3)写出t与Q的函数解析式;
(4)如果准备在 5 h 内将满池水排空,那么每小时的排水量至少为多少
(5)已知排水管的最大排水量为每小时 12 m ,那么最少多长时间可将满池水排空
8.教室里的饮水机接通电源就进入自动程序:开机加热时每分钟上升10℃,加热到100℃后停止加热,水温开始下降,此时水温(单位:℃)与开机后用时(单位:min)成反比例关系,直至水温降至 30 ℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为 30 ℃时,接通电源后,水温y(单位:℃)和时间x(单位:min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30
C.7:45 D.7:50
9.某地计划用120~180 天(含 120 与 180 天)的时间建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需时间 y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式,并给出自变量 x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多 5 000 立方米,工期比原计划减少了 24 天,原计划和实际平均每天运送土石方各是多少万立方米
10.蓄电池的电压为定值.使用此电源时,电流I(单位:A)与电阻R(单位:Ω)之间的函数关系如图所示.
(1)蓄电池的电压是多少 你能写出这一函数的解析式吗
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器,限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内
R/Ω 3 4 5 6 7 8 9 10
I/A 4
11.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度 y(单位:mg/mL)与服药时间x(单位:h)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y关于x的函数解析式;
(2)问血液中药物浓度不低于 4 mg/mL 的持续时间为多少小时
12.某厂从 2020年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年度 2020 2021 2022 2023
投入技改资金x/万元 2.5 3 4 4.5
产品成本y/(万元/件) 7.2 6 4.5 4
(1)请你认真分析表中数据,从你所学习过的一次函数、反比例函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其他函数的理由,并求出它的解析式;
(2)按照这种变化规律,若 2024 年已投入技改资金5万元.
①预计生产成本每件比2023年降低多少万元
②如果打算在2024年把每件产品成本降低到 3.2万元,则还需投入技改资金多少万元 (结果精确到 0.01万元)
1. B 由题意知 vt=80×4,则
2. D 3. A
4.(1)144 V (3)0.72~ 72A 减小
(4)7.2~200 Ω
5.解(1)由题意,得10xy=100,则
(2)当x=2时,
6.解(1)设反比例函数的解析式为
因为题中函数图象经过点(4,32),则有
所以k=128,即y与S 的函数解析式为 (S>0).
(2)当面条粗 S=1.6 mm 时,面条的总长度是
7.解(1)蓄水池的容积是(
(2)增加排水管会使时间缩短,将满池水排空所需的时间t会减少.
(3)因为容积V=48 m ,所以t 与Q的函数解析式为
即每小时的排水量至少为 9.6 m .
(5)设最少用 x h 将满池水排空,根据题意,得12x≥48,解得x≥4,即最少用4 h可将满池水排空.
8. A 由于开机加热时每分钟上升10℃,因此从30℃到100 ℃需要7 min. 设一次函数解析式 为 y= 将 ( 0 ,30),(7,100)代入 解得 k =10,b=30,所以y=10x+30(0≤x≤7).当y=50时,x=2.设反比例函数解析式为 将(7,100)代入 得k=700.当y=30 时, 所以 当y=50时,x=14,如图所示.所以饮水机的一个循环周期为 / min,每一个循环周期内,在0≤x≤2及 时间段内,水温不超过50℃,可直接饮用.
对于选项 A.7:20~8:45 之间有85 min, 3=15,即饮水机位于第 4 次重复开机后的第 15 min,此时水温不超过50℃,可直接饮用,符合题意.逐一分析,可知选项 B,C,D不符合题意,因此应选 A.
9.解(1)由题意,得 把、y=120代入 得x=3;把y=180代入 得x=2,所以自变量x的取值范围是2≤x≤3.故
(2)设原计划平均每天运送土石方 x万立方米,则实际平均每天运送土石方(x+0.5)万立方米.
由题意,得
方程两边同乘 x(x+0.5),得 360(x+0.5)一360x=24x(x+0.5).
化简得.x +0.5x-7.5=0,角解得
经检验, 均是原方程的根,但 不符合实际意义,故舍去.
又2≤x≤3,所以x=2.5 满足条件,即原计划平均每天运送土石方 2.5 万立方米,实际平均每天运送土石方3万立方米.
10.分析 从题图来看,I和R之间是反比例函数关系.电压U 就相当于反比例函数中的k.要写出函数的解析式,实际上就是确定 k(U),只需要一个条件即可,而题图中已给出了一个点的坐标,所以这个问题就解决了,填表实际上是已知自变量的值求函数值.
解(1)由题意,设函数解析式为
因为点A(9,4)在该函数图象上,所以U=IR=36(V),即蓄电池的电压是36 V.
所以所求函数解析式为
(2)表格中从左到右依次填:]12,9,7.2,6, ,4.5,3.6.
限制电流不超过10A,即Ⅰ最大为10A,代入关系式中得R=3.6Ω,为最小电阻,所以用电器的可变电阻应控制在R≥3.6 Ω 这个范围内.
11.解(1)当0≤x≤4时,设 y关于x 的函数解析式为 .将点(4,8)代入. 中,可得. 2,所以y=2x;
当4≤x≤10 时,设y关于x的函数解析式为 将点(4,8)代入 中,可得 32,所以 因此血液中药物浓度上升阶段的函数解析式为 y=2x(0≤x≤4),下降阶段的函数解析式为
(2)将y=4代入 y=2x中,得x=2;将y=4代入 中,得x=8,则血液中药物浓度不低于4 mg/mL 的持续时间为8-2=6(h).
12.解(1)若为一次函数,设其解析式为. 因为当x=2.5时,y=7.2;当x=3时,y=6,
所以 解得
所以一次函数的解析式为y=-2.4x+13.2.把x=4时,y=4.5代入此函数解析式,得左边≠右边.故不是一次函数.
若为反比例函数,设其解析式为 当x=2.5时,y=7.2,可得 得 所以反比例函数解析式为
验证:当x=3时, 符合反比例函数.
同理可验证:当 x=4 时,y=4. 5; 当 x=4. 5 时,y=4成立.故可用反比例函数 表示其变化规律.
(2)①当x=5时,
因为4—3.6=0.4(万元),所以预计生产成本每件比 2023 年降低 0.4 万元.
②当y=3.2时, 得x=5.625.
因为 5.625-5=0.625≈0.63(万元),
所以还需投入技改资金约0.63万元.
