26.1.2 反比例函数的图像和性质课后同步作业(含答案)
文档属性
| 名称 | 26.1.2 反比例函数的图像和性质课后同步作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 944.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览


文档简介
26.1.2反比例函数的图像和性质课后同步作业测评
1.已知在反比例函数 的图象的每一支上,y都随 x 的增大而增大,则 k 的值可以是( )
A. 1 B.0 C.1 D.2
2.若点A(-3,y ),B(-2,y ),C(1,y )都在反比例函数 的图象上,则y ,y ,y 的大小关系是( )
3.如图,过反比例函数 (x>0)的图象上任意两点 A,B分别作x轴的垂线,垂足分别为 C, D, 连 接 OA, OB. 设 △AOC 和△BOD的面积分别是S ,S ,比较它们的大小,可得( )
D.大小关系不能确定
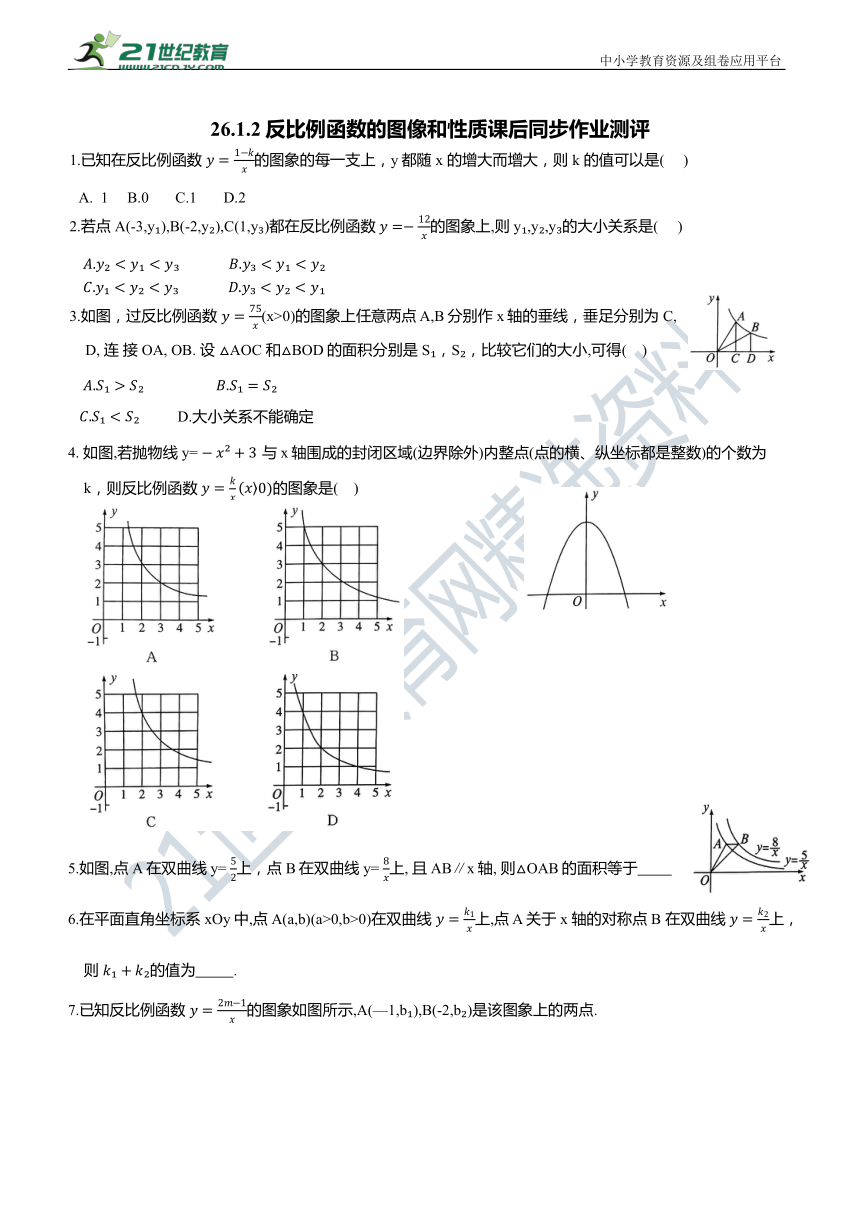
4. 如图,若抛物线 y= 与x轴围成的封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为 k,则反比例函数 的图象是( )
5.如图,点A 在双曲线y= 上,点B在双曲线 y= 上, 且AB∥x轴, 则△OAB的面积等于
6.在平面直角坐标系 xOy中,点A(a,b)(a>0,b>0)在双曲线 上,点 A 关于 x 轴的对称点B 在双曲线 上,则 的值为 .
7.已知反比例函数 的图象如图所示,A(—1,b ),B(-2,b )是该图象上的两点.
(1)比较b 与 b 的大小;
(2)求 m 的取值范围.
8.如图,A 是反比例函数y= 图象上任意一点,AB⊥y轴,垂足为点B,C是x 轴上的动点,则△ABC的面积为( )
A.1 B.2
C.4 D.不能确定
9.已知两个反比例函数 y 和 在第一象限内的图象如图所示,点 P 在 的图象上,PC⊥x轴于点C,交 的图象于点A,PD⊥y轴于点D,交 的图象于点B,则当点 P在 的图象上运动时,以下结论:
中小学教育资源及组卷应用平台
①△ODB 与△OCA的面积相等;
②四边形 PAOB 的面积不会发生变化;
③PA与PB 始终相等;
④当点A 是线段PC 的中点时,点 B一定是线段 PD的中点.
其中一定正确的是 .(把你认为正确结论的序号都填上)
10.如图,在平面直角坐标系中,四边形 OABC是矩形,D(1,4)是 BC 的中点,反比例函数 的图象经过点 D,并交 AB 于点E.
(1)求 k 的值;
(2)求五边形 OAEDC的面积S.
11.如图,在平面直角坐标系中,反比例函数. (x>0)的图象和矩形ABCD在第一象限,AD平行于 x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出 B,C,D三点的坐标;
(2)若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求出矩形的平移距离和反比例函数的解析式.
12.如图,正方形OABC的面积为 4,O为坐标原点,点B在函数 的图象上,P(m,n)是函数 x<0)的图象上异于点B的任意一点,过点 P分别作x轴、y轴的垂线,垂足分别为E,F.
(1)设矩形 OEPF 的面积为 S ,判断 S 与点 P的位置是否有关(不必说明理由);
(2)从矩形 OEPF 的面积中减去其与正方形OABC 重合部分的面积,剩余面积记为 S ,写出 S 关于 m 的函数解析式,并标明m的取值范围.
1. D 由题意可知1-k<0,所以k>1.故选 D.
2. B 当 x=-3 时,当 x=-2 时, 当 x=1 时, 所以 y3. B
4. D 对于 ,当 y=0 时, 当 x=0时,y=3.因此抛物线 与 x 轴围成封闭区域内的整点为(-1,1),(0,1),(0,2),(1,1),共4个,即 k=4,故选 D.
5. 延长BA交y轴于点C,
6.0 ∵点A(a,b)(a>0,b>0)在双曲线 上,
又点A与点B 关于x轴对称,∴点.B(a,-b).
∵点B在双曲线 上,
7.解(1)由题图可知,双曲线的两支分别位于第一、第三象限,在每个象限内y随x的增大而减小.
因为-2<-1<0,所以
(2)由题图知,2m-1>0,解得
8. A 设点A的坐标是(m,n),则mn=2,AB=m,△ABC的边AB上的高等于n,△ABC的面积 故选 A.
9.①②④
10.解(1)把点D(1,4)的坐标代入 得k=1×4=4.
(2)∵四边形 OABC 是矩形,D(1,4)是BC 的中点,∴BC=2CD=2. ∴点B坐标为(2,4).
把x=2代入 得 ∴点E(2,
∴五边形OAEDC的面积S=2×4-1=7.
11.解(1)点B(2,4),C(6,4),D(6,6).
(2)如图,矩形 ABCD 平移后得到矩形A'B'C'D',设平移距离为a,则点A′(2,6-a),C′(6,4-a).
因为点A'、点C'在 的图象上,所以2(6-a)=6(4-a),解得a=3.
所以点A′的坐标为(2,3).
故所求反比例函数的解析式为
12.解(1)S 与点 P 的位置无关.
(2)当点 P 在点 B 上方时, m<0);当点P在点B下方时,
1.已知在反比例函数 的图象的每一支上,y都随 x 的增大而增大,则 k 的值可以是( )
A. 1 B.0 C.1 D.2
2.若点A(-3,y ),B(-2,y ),C(1,y )都在反比例函数 的图象上,则y ,y ,y 的大小关系是( )
3.如图,过反比例函数 (x>0)的图象上任意两点 A,B分别作x轴的垂线,垂足分别为 C, D, 连 接 OA, OB. 设 △AOC 和△BOD的面积分别是S ,S ,比较它们的大小,可得( )
D.大小关系不能确定
4. 如图,若抛物线 y= 与x轴围成的封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为 k,则反比例函数 的图象是( )
5.如图,点A 在双曲线y= 上,点B在双曲线 y= 上, 且AB∥x轴, 则△OAB的面积等于
6.在平面直角坐标系 xOy中,点A(a,b)(a>0,b>0)在双曲线 上,点 A 关于 x 轴的对称点B 在双曲线 上,则 的值为 .
7.已知反比例函数 的图象如图所示,A(—1,b ),B(-2,b )是该图象上的两点.
(1)比较b 与 b 的大小;
(2)求 m 的取值范围.
8.如图,A 是反比例函数y= 图象上任意一点,AB⊥y轴,垂足为点B,C是x 轴上的动点,则△ABC的面积为( )
A.1 B.2
C.4 D.不能确定
9.已知两个反比例函数 y 和 在第一象限内的图象如图所示,点 P 在 的图象上,PC⊥x轴于点C,交 的图象于点A,PD⊥y轴于点D,交 的图象于点B,则当点 P在 的图象上运动时,以下结论:
中小学教育资源及组卷应用平台
①△ODB 与△OCA的面积相等;
②四边形 PAOB 的面积不会发生变化;
③PA与PB 始终相等;
④当点A 是线段PC 的中点时,点 B一定是线段 PD的中点.
其中一定正确的是 .(把你认为正确结论的序号都填上)
10.如图,在平面直角坐标系中,四边形 OABC是矩形,D(1,4)是 BC 的中点,反比例函数 的图象经过点 D,并交 AB 于点E.
(1)求 k 的值;
(2)求五边形 OAEDC的面积S.
11.如图,在平面直角坐标系中,反比例函数. (x>0)的图象和矩形ABCD在第一象限,AD平行于 x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出 B,C,D三点的坐标;
(2)若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求出矩形的平移距离和反比例函数的解析式.
12.如图,正方形OABC的面积为 4,O为坐标原点,点B在函数 的图象上,P(m,n)是函数 x<0)的图象上异于点B的任意一点,过点 P分别作x轴、y轴的垂线,垂足分别为E,F.
(1)设矩形 OEPF 的面积为 S ,判断 S 与点 P的位置是否有关(不必说明理由);
(2)从矩形 OEPF 的面积中减去其与正方形OABC 重合部分的面积,剩余面积记为 S ,写出 S 关于 m 的函数解析式,并标明m的取值范围.
1. D 由题意可知1-k<0,所以k>1.故选 D.
2. B 当 x=-3 时,当 x=-2 时, 当 x=1 时, 所以 y
4. D 对于 ,当 y=0 时, 当 x=0时,y=3.因此抛物线 与 x 轴围成封闭区域内的整点为(-1,1),(0,1),(0,2),(1,1),共4个,即 k=4,故选 D.
5. 延长BA交y轴于点C,
6.0 ∵点A(a,b)(a>0,b>0)在双曲线 上,
又点A与点B 关于x轴对称,∴点.B(a,-b).
∵点B在双曲线 上,
7.解(1)由题图可知,双曲线的两支分别位于第一、第三象限,在每个象限内y随x的增大而减小.
因为-2<-1<0,所以
(2)由题图知,2m-1>0,解得
8. A 设点A的坐标是(m,n),则mn=2,AB=m,△ABC的边AB上的高等于n,△ABC的面积 故选 A.
9.①②④
10.解(1)把点D(1,4)的坐标代入 得k=1×4=4.
(2)∵四边形 OABC 是矩形,D(1,4)是BC 的中点,∴BC=2CD=2. ∴点B坐标为(2,4).
把x=2代入 得 ∴点E(2,
∴五边形OAEDC的面积S=2×4-1=7.
11.解(1)点B(2,4),C(6,4),D(6,6).
(2)如图,矩形 ABCD 平移后得到矩形A'B'C'D',设平移距离为a,则点A′(2,6-a),C′(6,4-a).
因为点A'、点C'在 的图象上,所以2(6-a)=6(4-a),解得a=3.
所以点A′的坐标为(2,3).
故所求反比例函数的解析式为
12.解(1)S 与点 P 的位置无关.
(2)当点 P 在点 B 上方时, m<0);当点P在点B下方时,
