圆柱的表面积和体积经典题型课堂检验拔高篇(含答案)数学六年级下册人教版
文档属性
| 名称 | 圆柱的表面积和体积经典题型课堂检验拔高篇(含答案)数学六年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 453.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 19:56:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆柱的表面积和体积经典题型课堂检验(拔高篇)数学六年级下册人教版
一、选择题
1.一个圆柱的侧面展开后是一个正方形,它的底面半径是3cm,它的高是( )厘米。
A.6 B.18.84 C.28.26 D.37.68
2.一个圆柱形玻璃鱼灯,底面直径是20厘米,把里面的一条鱼捞出来后水面下降了0.2厘米,这条鱼的体积是( )立方厘米。
A. B. C. D.
3.如图,长方形的长是2厘米,宽是1厘米。分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱,这两个圆柱的体积( )。
A.甲大 B.乙大
C.同样大 D.无法判断谁大
4.包装盒长32cm、宽2cm、高1cm。圆柱形的零件底面直径2cm、高1cm,这个包装盒最多能放( )个零件。
A.25 B.32 C.8 D.16
5.底面积是28.26dm2的圆柱体的高增加3dm,体积增加( )dm3。
A.28.26 B.14.13 C.84.78 D.56.52
6.把一个高6dm、底面半径2dm的圆柱切成若干等份,拼成一个近似的长方体(如图),这时表面积( )。
A.增加了24dm2 B.增加了12dm2 C.减少了24dm2 D.减少了12dm2
二、填空题
7.一顶帽子,上面是直径2dm,高1dm的圆柱形(有帽顶),帽檐部分是一个宽1dm的圆环,做这顶帽子,至少要用( )的布料。(接头处忽略不计)
8.美术课上,张老师教同学们用一张长方形卡纸做成一个圆柱。先把长方形卡纸剪成两个大小相等的圆和一个长方形(如图),分别作圆柱的底面和侧面,通过粘合就成了一个圆柱。这个圆柱表面积是( )cm2,体积是( )cm3。(接头与卡纸的厚度不计)
9.在一个长方体纸盒中,装了一个底面直径8厘米,高12厘米的圆柱形杯子(如图)。这个纸盒的容积至少是( )立方厘米。
10.数学课上,小明用一张长10厘米、宽8厘米的长方形纸,剪一个最大的圆,这个圆的周长是( )厘米,小方把一根底面直径10厘米、长50厘米的圆柱形木料等距离截成3段小圆柱,表面积增加( )平方厘米。
11.如图长方形长3分米,宽2分米。以宽边的中点连线(如图)为轴旋转一周所形成的立体图形的表面积是( )平方分米,以宽边为轴旋转一周所形成的立体图形的体积是( )立方分米(计算结果保留π)。
12.如图,把一个底面半径为2dm,高为5dm的圆柱等分成若干份,拼成一个近似的长方体,这个长方体的体积是( )dm3,长方体的表面积比原来圆柱的表面积大( )dm2。
三、判断题
13.一个圆柱的底面半径是d,高是πd,它的侧面展开图是正方形。( )
14.两个圆柱的体积相等那么它们的侧面积也相等。( )
15.如果圆柱的底面半径和高相等,那么它的两个底面积的和等于它的侧面积。( )
16.任意两个相同的圆和一个曲面就可以组成一个圆柱。( )
17.一个圆柱的底面半径扩大4倍,高不变,它的侧面积就扩大16倍. ( )
四、计算题
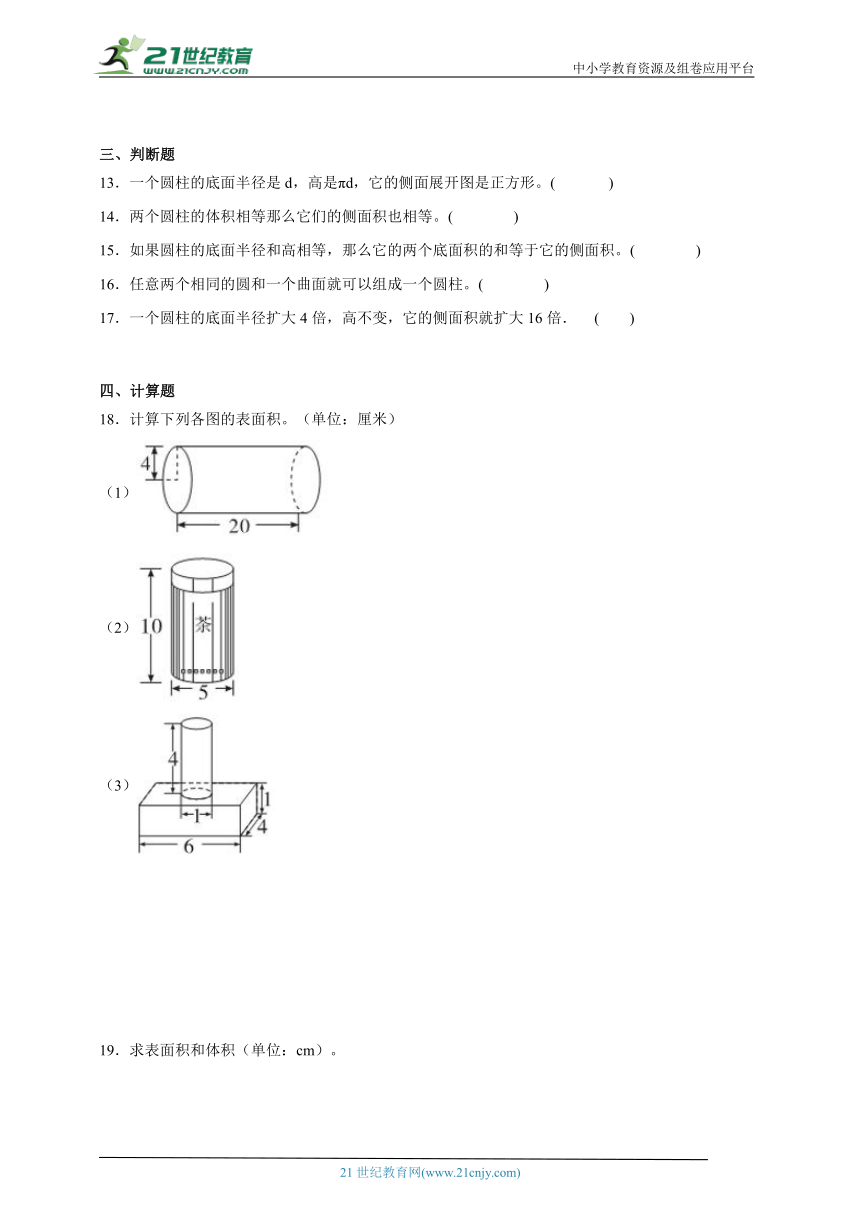
18.计算下列各图的表面积。(单位:厘米)
(1)
(2)
(3)
19.求表面积和体积(单位:cm)。
五、解答题
20.依依家来了3位客人,依依拿出20毫升浓缩果汁,浓缩果汁与水按1∶50给客人冲果汁喝,用如图所示的玻璃杯将果汁倒至处,依依和客人每人一杯够吗?
21.一台压路机的前轮直径是2米,宽3米,每分钟转动15周,在工作中一直滚动前行,压路机每分钟压路的面积是多少平方米?
22.理发店的墙壁上悬挂着一个半圆柱体储水桶如图所示。已知水桶的高是5分米,底面半圆的直径4分米。
(1)这个储水桶与墙面的接触面积有多少平方分米?
(2)这个储水桶最多储水多少升?
(3)储水桶下出水管的内直径是2厘米,装满水后打开水龙头时,水速为20厘米/秒,这桶水能持续使用多少秒?
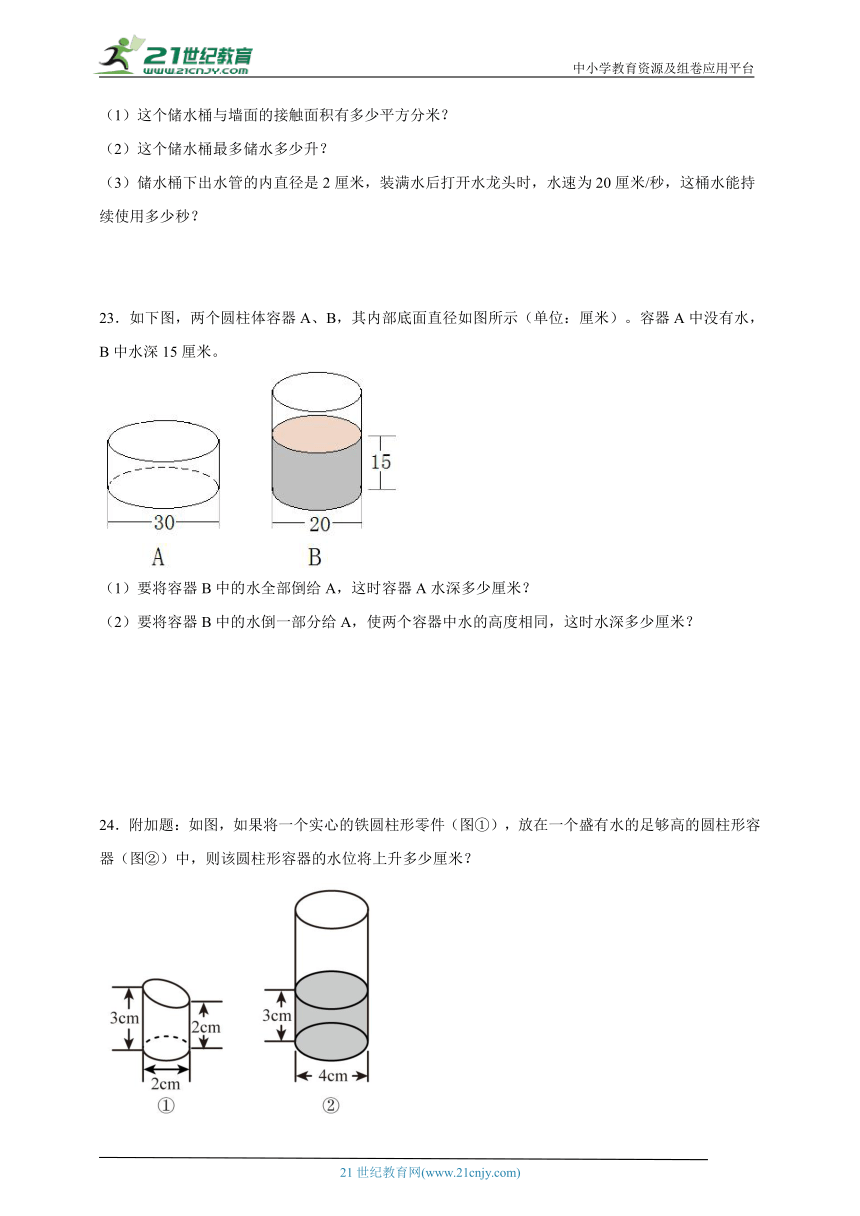
23.如下图,两个圆柱体容器A、B,其内部底面直径如图所示(单位:厘米)。容器A中没有水,B中水深15厘米。
(1)要将容器B中的水全部倒给A,这时容器A水深多少厘米?
(2)要将容器B中的水倒一部分给A,使两个容器中水的高度相同,这时水深多少厘米?
24.附加题:如图,如果将一个实心的铁圆柱形零件(图①),放在一个盛有水的足够高的圆柱形容器(图②)中,则该圆柱形容器的水位将上升多少厘米?
25.劳动活动周,中心路小学组织学生回收废旧垃圾,不仅能减少碳排放,而且还可以利用它们制作出很多精美的手工艺品。下面是同学们收集到的一个未喝完的废旧饮料瓶。同学们准备将它做成一个精美的手工笔筒。如图,底面是圆形,半径是3厘米,这个饮料瓶的容积是多少立方厘米?
参考答案:
1.B
【分析】侧面展开图是正方形,所以圆柱的底面周长与圆柱的高相等,根据圆柱的底面周长=,可以求出圆柱的高。
【详解】
=
=(厘米)
它的高是18.84厘米。
故答案为:B
【点睛】
2.C
【分析】由题意可知,水面下降的那部分水的体积就是这条鱼的体积,根据圆柱的体积,把直径20厘米,高0.2厘米代入圆柱的体积公式计算即可求出这条鱼的体积。
【详解】×(20÷2)2×0.2
=×102×0.2
=×100×0.2
=(立方厘米)
所以,这条鱼的体积是立方厘米。
故答案为:C
3.B
【分析】观察图可知,甲图旋转后的圆柱底面半径是1厘米,高是2厘米,乙图旋转后的圆柱底面半径是2厘米,高是1厘米,根据圆柱的体积公式:V=πr2h,据此列式计算,然后比较大小即可。
【详解】甲的体积:
3.14×12×2
=3.14×1×2
=3.14×2
=6.28(立方厘米)
乙的体积:
3.14×22×1
=3.14×4×1
=12.56×1
=12.56(立方厘米)
12.56>6.28
则乙的体积比较大。
故答案为:B
4.D
【分析】根据题干可得,包装盒的高是1厘米,零件的高也是1厘米,所以包装盒内只能放一层,包装盒的宽和零件的底面直径也相等,也只能放1列,由此只要看它们的底面长能放几个零件即可。
【详解】32÷2=16(个)
则这个包装盒最多能放16个零件。
故答案为:D
5.C
【分析】圆柱体的体积=底面积×高,当高增加3dm,体积增加=底面积×增加的高。
【详解】由分析可知,圆柱体体积增加:28.26×3=84.78(dm3)
故答案为:C
6.A
【分析】如上图,把圆柱转化成长方体后,长方体上面、下面分别等于圆柱的上、下底面;长方体的前面和后面的面积和等于圆柱的侧面积。也就是转化后的长方体的表面积比圆柱的表面积多了长方体左、右面的面积和。先用圆柱的高(6dm)乘底面半径(2dm)求出长方体的右面(或左面)的面积,再乘2求出长方体左、右面的面积和,即增加的表面积。
【详解】6×2×2=24(dm2)
所以这时表面积增加了24dm2。
故答案为:A
【点睛】把圆柱转化成长方体后,转化后的长方体的表面积比圆柱的表面积多了两个长为圆柱的高,宽为圆柱的底面半径的长方形的面积。
7.18.84dm2/18.84平方分米
【分析】布料面积=圆柱侧面积+底面积+帽檐面积,圆柱侧面积=底面周长×高,圆环面积=π(R2-r2),据此列式计算。
【详解】2÷2=1(dm)
1+1=2(dm)
3.14×2×1+3.14×12+3.14×(22-12)
=6.28+3.14×1+3.14×(4-1)
=6.28+3.14+3.14×3
=6.28+3.14+9.42
=18.84(dm2)
【点睛】关键是掌握并灵活运用圆柱表面积公式和圆环面积公式。
8. 125.6 100.48
【分析】看图,圆柱底面直径的2倍是圆柱的高,圆柱底面周长加上底面直径是16.56cm。底面周长=3.14×底面直径,底面半径×2=底面直径,那么3.14×底面直径+底面直径=16.56cm,所以将16.56cm除以(1+3.14)可先求出底面直径,从而求出底面半径。圆柱表面积=底面积×2+侧面积,圆柱体积=底面积×高,将数据代入公式求出它的表面积和体积即可。
【详解】底面直径:
16.56÷(1+3.14)
=16.56÷4.14
=4(cm)
底面半径:4÷2=2(cm)
表面积:
3.14×22×2+3.14×4×(4×2)
=3.14×8+3.14×32
=3.14×(8+32)
=3.14×40
=125.6(cm2)
体积:
3.14×22×(4×2)
=3.14×4×8
=100.48(cm3)
所以,这个圆柱的表面积是125.6cm2,体积是100.48cm3。
【点睛】本题考查了圆柱的表面积和体积,灵活运用公式是解题的关键。
9.768
【分析】根据题意,这个纸盒的高至少是12厘米,长和宽至少是8厘米。长方体容积=长×宽×高,据此列式求出这个纸盒的容积至少是多少立方厘米。
【详解】8×8×12=768(立方厘米)
所以,这个纸盒的容积至少是768立方厘米。
【点睛】本题考查了圆柱的认识、长方体的容积,熟记长方体容积公式是解题关键。
10. 25.12 314
【分析】(1)根据题意可知,在这张长方形纸上剪一个最大的圆,这个圆的直径等于长方形的宽,根据圆的周长公式:C=πd,把数据代入公式解答。
(2)根据题意可知,把这根圆柱形木料横截成3段,需要截2次,每截一次就增加2个截面的面积,由此可知,把它截成3段表面积比原来增加4个截面的面积,根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】(1)3.14×8=25.12(厘米)
这个圆的周长是25.12厘米。
(2)3.14×(10÷2)2×4
=3.14×25×4
=78.5×4
=314(平方厘米)
表面积增加314平方厘米。
【点睛】此题主要考查圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式。
11. 8π 18π
【分析】根据圆柱的定义:一个长方形长3分米,宽2分米,以宽边的中点连线为轴旋转一周,会得到一个圆柱形,这个圆柱的底面半径是(2÷2)分米,高是3分米,根据圆柱的表面积=侧面积+底面积×2,求出表面积;以宽为轴旋转一周,形成的圆柱的底面半径是3分米,高是2分米,由此根据圆柱的体积=底面积×高,把数据代入公式解答即可。
【详解】表面积:2×π×3+π×(2÷2)2×2
=6π+π×2
=6π+2π
=8π(平方分米)
体积:π×32×2
=π×9×2
=18π(立方分米)
如图长方形长3分米,宽2分米。以宽边的中点连线(如图)为轴旋转一周所形成的立体图形的表面积是8π平方分米,以宽边为轴旋转一周所形成的立体图形的体积是18π立方分米。
【点睛】熟练掌握圆柱的特征,圆柱的表面积公式以及体积公式的灵活运用。
12. 62.8 20
【分析】如图,将圆柱等分成若干份,拼成一个近似的长方体,圆柱体积=长方体体积,根据圆柱体积=底面积×高,求出长方体体积;长方体的表面积比原来圆柱的表面积多了两个长方形,长方形的长=圆柱的高,长方形的宽=圆柱底面半径,根据长方形面积=长×宽,求出一个长方形面积,乘2,是长方体比圆柱大的表面积。
【详解】3.14×22×5
=3.14×4×5
=62.8(dm3)
5×2×2=20(dm2)
这个长方体的体积是62.8dm3,长方体的表面积比原来圆柱的表面积大20dm2。
【点睛】关键是熟悉圆柱体积公式推导过程,掌握并灵活运用圆柱体积公式。
13.×
【分析】因为圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高,一个圆柱的底面半径是d,则底面周长是2πd,高是πd,则底面周长与高不相等,所以它的侧面展开图是长方形,不是正方形。据此解答。
【详解】一个圆柱的底面半径是d,高是πd,底面周长是2πd,与高不相等,所以它的侧面展开图是长方形。
故答案为:×
14.×
【详解】可举例来说明:
r1=1厘米
h1=20厘米
V1=3.14×12×20
=3.14×20
=62.8(立方厘米)
r2=2厘米
h2=5厘米
V2=3.14×22×5
=12.56×5
=62.8(立方厘米)
两个圆柱体积相同。
S1=3.14×1×2×20
=6.28×20
=125.6(平方厘米)
S2=3.14×2×2×5
=12.56×5
=62.8(平方厘米)
125.6平方厘米≠62.8平方厘米
综上可得:两个圆柱的体积相等那么它们的侧面积也相等,这种说法是错误的。
故答案为:×
15.√
【详解】如果圆柱的半径为r。高为h,那么圆柱的两个底面积列式为2r ,侧面积列式为2rh,如果圆柱的底面半径和高相等,那么它的侧面积也可以写成2r ,所以它的两个底面积和它的侧面积相等。
16.×
【分析】圆柱的两个底面相等,且曲面的一条边与底面周长相等时才可以组成一个圆柱,由此解答即可。
【详解】任意两个相同的圆和一个曲面不一定组成一个圆柱。
故答案为:×。
【点睛】熟练掌握圆柱的特征是解答本题的关键。
17.错误
【详解】【解答】一个圆柱的底面半径扩大4倍,高不变,它的侧面积就扩大4倍.原题说法错误
故答案为错误
【分析】圆柱的底面半径扩大4倍,底面周长就扩大4倍,因为侧面积=底面周长×高,高不变,圆柱的侧面积的变化情况与底面周长的变化情况相同.
18.(1)602.88平方厘米;(2)196.25平方厘米;(3)80.56平方厘米
【分析】(1)(2)直接根据圆柱表面积=底面积×2+侧面积,列式计算;(3)将圆柱上边的面平移到下边,用长方体表面积+圆柱侧面积即可。
【详解】(1)3.14×4×2+3.14×4×2×20
=100.48+502.4
=602.88(平方厘米)
(2)5÷2=2.5(厘米)
3.14×2.5×2+3.14×5×10
=39.25+157
=196.25(平方厘米)
(3)(6×4+6×1+4×1)×2+3.14×1×4
=(24+6+4)×2+12.56
=34×2+12.56
=68+12.56
=80.56(平方厘米)
【点睛】本题考查了圆柱和组合体的表面积,圆柱侧面积=底面周长×高。
19.151.62cm2;113.04cm3
【分析】半个圆柱的表面积=圆柱的底面积+圆柱的侧面积的一半+长方形的面积;代入数据计算即可。
根据V柱=πr2h求出圆柱的体积,再除以2就是半个圆柱的体积。
【详解】圆柱的底面积:3.14×2
=3.14×9
=28.26(cm2)
圆柱的侧面积的一半:3.14×6×8÷2=75.36(cm2)
长方形的面积:6×8=48(cm2)
半个圆柱的表面积:28.26+75.36+48=151.62(cm2)
半个圆柱的体积:3.14×2×8÷2
=28.26×8÷2
=226.08÷2
=113.04(cm3)
【点睛】根据图形特点灵活运用圆柱的表面积公式和体积公式。
20.不够
【分析】根据题意,求出20毫升浓缩果汁按1∶50,可配果汁多少,再利用圆柱的体积公式求出玻璃杯的体积,再进行比较即可。
【详解】20×50=1000(毫升)
3.14×(6÷2)2×15××4
=3.14×9×(15×)×4
=28.26×10×4
=282.6×4
=1130.4(立方厘米)
=1130.4(毫升)
1000毫升<1130.4毫升
答:每人一杯不够。
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
21.282.6平方米
【分析】压路机的前轮是一个圆柱体,压路机滚动一周的压路面积等于圆柱的侧面积,根据“”表示出压路机滚动一周的压路面积,最后乘压路机每分钟转动的周数求出压路机每分钟压路的面积,据此解答。
【详解】3.14×2×3×15
=6.28×3×15
=18.84×15
=282.6(平方米)
答:压路机每分钟压路的面积是282.6平方米。
【点睛】本题主要考查圆柱侧面积公式的应用,熟记公式是解答题目的关键。
22.(1)20平方分米
(2)31.4升
(3)500秒
【分析】(1)求水桶与墙面的接触面积就是求圆柱切面的长方形面积,长方形的宽等于直径,长方形的长等于圆柱的高;
(2)这个储水桶的容积等于整个圆柱容积的一半,圆柱的容积=底面积×高,用圆柱的容积乘二分之一就是这个水桶的容积;
(3)先将水桶的单位换算成毫升,求出每秒流出水的体积,水桶的容积÷每秒流出水的体积=流水持续的时间。
【详解】(1)5×4=20(平方分米)
答:这个储水桶与墙面的接触面积有20平方分米
(2)3.14×(4÷2)2×5÷2
=3.14×20÷2
=31.4(立方分米)
=31.4(升)
答:这个储水桶最多储水31.4升。
(3)31.4升=31400毫升
3.14×(2÷2)2×20
=3.14×20
=62.8(立方厘米)
=62.8(毫升)
31400÷62.8=500(秒)
答:这桶水能持续使用500秒。
【点睛】再求这个圆柱的接触面积是要知道是求这个长方形的面积,理解长方形的宽与直径是相等的,长与圆柱的高是相等的;求水桶容积的时候重点是知道水桶的容积是圆柱容积的一半。
23.(1)厘米
(2)4.6厘米
【分析】(1)根据圆柱的体积公式:V=πr2h,据此求出水的体积,再用水的体积除以容器A的底面积即可求出容器A的水深;
(2)由题意可知,设这时水深x厘米,根据容器A的水的体积+容器B的水的体积=水的总体积,据此列方程解答即可。
【详解】(1)3.14×(20÷2)2×15÷[3.14×(30÷2)2]
=3.14×100×15÷[3.14×225]
=3.14×100×15÷706.5
=4710÷706.5
=(厘米)
答:这时容器A水深厘米。
(2)解:设这时水深x厘米。
3.14×(30÷2)2×x+3.14×(20÷2)2×x=3.14×(20÷2)2×15
3.14×225x+3.14×100x=3.14×100×15
706.5x+314x=4710
1020.5x=4710
1020.5x÷1020.5=4710÷1020.5
x≈4.6
答:这时水深4.6厘米。
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
24.0.625厘米
【分析】圆柱体积=底面积×高,图①零件的体积=高2厘米的圆柱体积+高(3-2)厘米圆柱体积的一半,图①零件的体积÷图②容器底面积=水位上升高度,据此列式解答。
【详解】2÷2=1(厘米)
3.14×12×2+3.14×12×(3-2)÷2
=3.14×1×2+3.14×1×1÷2
=6.28+1.57
=7.85(立方厘米)
7.85÷[3.14×(4÷2)2]
=7.85÷[3.14×22]
=7.85÷[3.14×4]
=7.85÷12.56
=0.625(厘米)
答:该圆柱形容器的水位将上升0.625厘米。
【点睛】关键是掌握并灵活运用圆柱体积公式。
25.226.08立方厘米
【分析】饮料瓶的底面半径和正放时饮液面的高度已知,根据圆柱的体积公式:V=,则可以求出瓶内饮料的体积,同样的方法,可以求出倒放时空余部分的体积,瓶子的容积=饮料的体积+倒放时空余部分的体积。据此解答。
【详解】3.14×32×6+3.14×32×2
=3.14×9×6+3.14×9×2
=169.56+56.52
=226.08(立方厘米)
答:这个饮料瓶的容积是226.08立方厘米。
【点睛】此题解答关键是利用体积不变的特性,把不规则图形转化为规则图形来计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱的表面积和体积经典题型课堂检验(拔高篇)数学六年级下册人教版
一、选择题
1.一个圆柱的侧面展开后是一个正方形,它的底面半径是3cm,它的高是( )厘米。
A.6 B.18.84 C.28.26 D.37.68
2.一个圆柱形玻璃鱼灯,底面直径是20厘米,把里面的一条鱼捞出来后水面下降了0.2厘米,这条鱼的体积是( )立方厘米。
A. B. C. D.
3.如图,长方形的长是2厘米,宽是1厘米。分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱,这两个圆柱的体积( )。
A.甲大 B.乙大
C.同样大 D.无法判断谁大
4.包装盒长32cm、宽2cm、高1cm。圆柱形的零件底面直径2cm、高1cm,这个包装盒最多能放( )个零件。
A.25 B.32 C.8 D.16
5.底面积是28.26dm2的圆柱体的高增加3dm,体积增加( )dm3。
A.28.26 B.14.13 C.84.78 D.56.52
6.把一个高6dm、底面半径2dm的圆柱切成若干等份,拼成一个近似的长方体(如图),这时表面积( )。
A.增加了24dm2 B.增加了12dm2 C.减少了24dm2 D.减少了12dm2
二、填空题
7.一顶帽子,上面是直径2dm,高1dm的圆柱形(有帽顶),帽檐部分是一个宽1dm的圆环,做这顶帽子,至少要用( )的布料。(接头处忽略不计)
8.美术课上,张老师教同学们用一张长方形卡纸做成一个圆柱。先把长方形卡纸剪成两个大小相等的圆和一个长方形(如图),分别作圆柱的底面和侧面,通过粘合就成了一个圆柱。这个圆柱表面积是( )cm2,体积是( )cm3。(接头与卡纸的厚度不计)
9.在一个长方体纸盒中,装了一个底面直径8厘米,高12厘米的圆柱形杯子(如图)。这个纸盒的容积至少是( )立方厘米。
10.数学课上,小明用一张长10厘米、宽8厘米的长方形纸,剪一个最大的圆,这个圆的周长是( )厘米,小方把一根底面直径10厘米、长50厘米的圆柱形木料等距离截成3段小圆柱,表面积增加( )平方厘米。
11.如图长方形长3分米,宽2分米。以宽边的中点连线(如图)为轴旋转一周所形成的立体图形的表面积是( )平方分米,以宽边为轴旋转一周所形成的立体图形的体积是( )立方分米(计算结果保留π)。
12.如图,把一个底面半径为2dm,高为5dm的圆柱等分成若干份,拼成一个近似的长方体,这个长方体的体积是( )dm3,长方体的表面积比原来圆柱的表面积大( )dm2。
三、判断题
13.一个圆柱的底面半径是d,高是πd,它的侧面展开图是正方形。( )
14.两个圆柱的体积相等那么它们的侧面积也相等。( )
15.如果圆柱的底面半径和高相等,那么它的两个底面积的和等于它的侧面积。( )
16.任意两个相同的圆和一个曲面就可以组成一个圆柱。( )
17.一个圆柱的底面半径扩大4倍,高不变,它的侧面积就扩大16倍. ( )
四、计算题
18.计算下列各图的表面积。(单位:厘米)
(1)
(2)
(3)
19.求表面积和体积(单位:cm)。
五、解答题
20.依依家来了3位客人,依依拿出20毫升浓缩果汁,浓缩果汁与水按1∶50给客人冲果汁喝,用如图所示的玻璃杯将果汁倒至处,依依和客人每人一杯够吗?
21.一台压路机的前轮直径是2米,宽3米,每分钟转动15周,在工作中一直滚动前行,压路机每分钟压路的面积是多少平方米?
22.理发店的墙壁上悬挂着一个半圆柱体储水桶如图所示。已知水桶的高是5分米,底面半圆的直径4分米。
(1)这个储水桶与墙面的接触面积有多少平方分米?
(2)这个储水桶最多储水多少升?
(3)储水桶下出水管的内直径是2厘米,装满水后打开水龙头时,水速为20厘米/秒,这桶水能持续使用多少秒?
23.如下图,两个圆柱体容器A、B,其内部底面直径如图所示(单位:厘米)。容器A中没有水,B中水深15厘米。
(1)要将容器B中的水全部倒给A,这时容器A水深多少厘米?
(2)要将容器B中的水倒一部分给A,使两个容器中水的高度相同,这时水深多少厘米?
24.附加题:如图,如果将一个实心的铁圆柱形零件(图①),放在一个盛有水的足够高的圆柱形容器(图②)中,则该圆柱形容器的水位将上升多少厘米?
25.劳动活动周,中心路小学组织学生回收废旧垃圾,不仅能减少碳排放,而且还可以利用它们制作出很多精美的手工艺品。下面是同学们收集到的一个未喝完的废旧饮料瓶。同学们准备将它做成一个精美的手工笔筒。如图,底面是圆形,半径是3厘米,这个饮料瓶的容积是多少立方厘米?
参考答案:
1.B
【分析】侧面展开图是正方形,所以圆柱的底面周长与圆柱的高相等,根据圆柱的底面周长=,可以求出圆柱的高。
【详解】
=
=(厘米)
它的高是18.84厘米。
故答案为:B
【点睛】
2.C
【分析】由题意可知,水面下降的那部分水的体积就是这条鱼的体积,根据圆柱的体积,把直径20厘米,高0.2厘米代入圆柱的体积公式计算即可求出这条鱼的体积。
【详解】×(20÷2)2×0.2
=×102×0.2
=×100×0.2
=(立方厘米)
所以,这条鱼的体积是立方厘米。
故答案为:C
3.B
【分析】观察图可知,甲图旋转后的圆柱底面半径是1厘米,高是2厘米,乙图旋转后的圆柱底面半径是2厘米,高是1厘米,根据圆柱的体积公式:V=πr2h,据此列式计算,然后比较大小即可。
【详解】甲的体积:
3.14×12×2
=3.14×1×2
=3.14×2
=6.28(立方厘米)
乙的体积:
3.14×22×1
=3.14×4×1
=12.56×1
=12.56(立方厘米)
12.56>6.28
则乙的体积比较大。
故答案为:B
4.D
【分析】根据题干可得,包装盒的高是1厘米,零件的高也是1厘米,所以包装盒内只能放一层,包装盒的宽和零件的底面直径也相等,也只能放1列,由此只要看它们的底面长能放几个零件即可。
【详解】32÷2=16(个)
则这个包装盒最多能放16个零件。
故答案为:D
5.C
【分析】圆柱体的体积=底面积×高,当高增加3dm,体积增加=底面积×增加的高。
【详解】由分析可知,圆柱体体积增加:28.26×3=84.78(dm3)
故答案为:C
6.A
【分析】如上图,把圆柱转化成长方体后,长方体上面、下面分别等于圆柱的上、下底面;长方体的前面和后面的面积和等于圆柱的侧面积。也就是转化后的长方体的表面积比圆柱的表面积多了长方体左、右面的面积和。先用圆柱的高(6dm)乘底面半径(2dm)求出长方体的右面(或左面)的面积,再乘2求出长方体左、右面的面积和,即增加的表面积。
【详解】6×2×2=24(dm2)
所以这时表面积增加了24dm2。
故答案为:A
【点睛】把圆柱转化成长方体后,转化后的长方体的表面积比圆柱的表面积多了两个长为圆柱的高,宽为圆柱的底面半径的长方形的面积。
7.18.84dm2/18.84平方分米
【分析】布料面积=圆柱侧面积+底面积+帽檐面积,圆柱侧面积=底面周长×高,圆环面积=π(R2-r2),据此列式计算。
【详解】2÷2=1(dm)
1+1=2(dm)
3.14×2×1+3.14×12+3.14×(22-12)
=6.28+3.14×1+3.14×(4-1)
=6.28+3.14+3.14×3
=6.28+3.14+9.42
=18.84(dm2)
【点睛】关键是掌握并灵活运用圆柱表面积公式和圆环面积公式。
8. 125.6 100.48
【分析】看图,圆柱底面直径的2倍是圆柱的高,圆柱底面周长加上底面直径是16.56cm。底面周长=3.14×底面直径,底面半径×2=底面直径,那么3.14×底面直径+底面直径=16.56cm,所以将16.56cm除以(1+3.14)可先求出底面直径,从而求出底面半径。圆柱表面积=底面积×2+侧面积,圆柱体积=底面积×高,将数据代入公式求出它的表面积和体积即可。
【详解】底面直径:
16.56÷(1+3.14)
=16.56÷4.14
=4(cm)
底面半径:4÷2=2(cm)
表面积:
3.14×22×2+3.14×4×(4×2)
=3.14×8+3.14×32
=3.14×(8+32)
=3.14×40
=125.6(cm2)
体积:
3.14×22×(4×2)
=3.14×4×8
=100.48(cm3)
所以,这个圆柱的表面积是125.6cm2,体积是100.48cm3。
【点睛】本题考查了圆柱的表面积和体积,灵活运用公式是解题的关键。
9.768
【分析】根据题意,这个纸盒的高至少是12厘米,长和宽至少是8厘米。长方体容积=长×宽×高,据此列式求出这个纸盒的容积至少是多少立方厘米。
【详解】8×8×12=768(立方厘米)
所以,这个纸盒的容积至少是768立方厘米。
【点睛】本题考查了圆柱的认识、长方体的容积,熟记长方体容积公式是解题关键。
10. 25.12 314
【分析】(1)根据题意可知,在这张长方形纸上剪一个最大的圆,这个圆的直径等于长方形的宽,根据圆的周长公式:C=πd,把数据代入公式解答。
(2)根据题意可知,把这根圆柱形木料横截成3段,需要截2次,每截一次就增加2个截面的面积,由此可知,把它截成3段表面积比原来增加4个截面的面积,根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】(1)3.14×8=25.12(厘米)
这个圆的周长是25.12厘米。
(2)3.14×(10÷2)2×4
=3.14×25×4
=78.5×4
=314(平方厘米)
表面积增加314平方厘米。
【点睛】此题主要考查圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式。
11. 8π 18π
【分析】根据圆柱的定义:一个长方形长3分米,宽2分米,以宽边的中点连线为轴旋转一周,会得到一个圆柱形,这个圆柱的底面半径是(2÷2)分米,高是3分米,根据圆柱的表面积=侧面积+底面积×2,求出表面积;以宽为轴旋转一周,形成的圆柱的底面半径是3分米,高是2分米,由此根据圆柱的体积=底面积×高,把数据代入公式解答即可。
【详解】表面积:2×π×3+π×(2÷2)2×2
=6π+π×2
=6π+2π
=8π(平方分米)
体积:π×32×2
=π×9×2
=18π(立方分米)
如图长方形长3分米,宽2分米。以宽边的中点连线(如图)为轴旋转一周所形成的立体图形的表面积是8π平方分米,以宽边为轴旋转一周所形成的立体图形的体积是18π立方分米。
【点睛】熟练掌握圆柱的特征,圆柱的表面积公式以及体积公式的灵活运用。
12. 62.8 20
【分析】如图,将圆柱等分成若干份,拼成一个近似的长方体,圆柱体积=长方体体积,根据圆柱体积=底面积×高,求出长方体体积;长方体的表面积比原来圆柱的表面积多了两个长方形,长方形的长=圆柱的高,长方形的宽=圆柱底面半径,根据长方形面积=长×宽,求出一个长方形面积,乘2,是长方体比圆柱大的表面积。
【详解】3.14×22×5
=3.14×4×5
=62.8(dm3)
5×2×2=20(dm2)
这个长方体的体积是62.8dm3,长方体的表面积比原来圆柱的表面积大20dm2。
【点睛】关键是熟悉圆柱体积公式推导过程,掌握并灵活运用圆柱体积公式。
13.×
【分析】因为圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高,一个圆柱的底面半径是d,则底面周长是2πd,高是πd,则底面周长与高不相等,所以它的侧面展开图是长方形,不是正方形。据此解答。
【详解】一个圆柱的底面半径是d,高是πd,底面周长是2πd,与高不相等,所以它的侧面展开图是长方形。
故答案为:×
14.×
【详解】可举例来说明:
r1=1厘米
h1=20厘米
V1=3.14×12×20
=3.14×20
=62.8(立方厘米)
r2=2厘米
h2=5厘米
V2=3.14×22×5
=12.56×5
=62.8(立方厘米)
两个圆柱体积相同。
S1=3.14×1×2×20
=6.28×20
=125.6(平方厘米)
S2=3.14×2×2×5
=12.56×5
=62.8(平方厘米)
125.6平方厘米≠62.8平方厘米
综上可得:两个圆柱的体积相等那么它们的侧面积也相等,这种说法是错误的。
故答案为:×
15.√
【详解】如果圆柱的半径为r。高为h,那么圆柱的两个底面积列式为2r ,侧面积列式为2rh,如果圆柱的底面半径和高相等,那么它的侧面积也可以写成2r ,所以它的两个底面积和它的侧面积相等。
16.×
【分析】圆柱的两个底面相等,且曲面的一条边与底面周长相等时才可以组成一个圆柱,由此解答即可。
【详解】任意两个相同的圆和一个曲面不一定组成一个圆柱。
故答案为:×。
【点睛】熟练掌握圆柱的特征是解答本题的关键。
17.错误
【详解】【解答】一个圆柱的底面半径扩大4倍,高不变,它的侧面积就扩大4倍.原题说法错误
故答案为错误
【分析】圆柱的底面半径扩大4倍,底面周长就扩大4倍,因为侧面积=底面周长×高,高不变,圆柱的侧面积的变化情况与底面周长的变化情况相同.
18.(1)602.88平方厘米;(2)196.25平方厘米;(3)80.56平方厘米
【分析】(1)(2)直接根据圆柱表面积=底面积×2+侧面积,列式计算;(3)将圆柱上边的面平移到下边,用长方体表面积+圆柱侧面积即可。
【详解】(1)3.14×4×2+3.14×4×2×20
=100.48+502.4
=602.88(平方厘米)
(2)5÷2=2.5(厘米)
3.14×2.5×2+3.14×5×10
=39.25+157
=196.25(平方厘米)
(3)(6×4+6×1+4×1)×2+3.14×1×4
=(24+6+4)×2+12.56
=34×2+12.56
=68+12.56
=80.56(平方厘米)
【点睛】本题考查了圆柱和组合体的表面积,圆柱侧面积=底面周长×高。
19.151.62cm2;113.04cm3
【分析】半个圆柱的表面积=圆柱的底面积+圆柱的侧面积的一半+长方形的面积;代入数据计算即可。
根据V柱=πr2h求出圆柱的体积,再除以2就是半个圆柱的体积。
【详解】圆柱的底面积:3.14×2
=3.14×9
=28.26(cm2)
圆柱的侧面积的一半:3.14×6×8÷2=75.36(cm2)
长方形的面积:6×8=48(cm2)
半个圆柱的表面积:28.26+75.36+48=151.62(cm2)
半个圆柱的体积:3.14×2×8÷2
=28.26×8÷2
=226.08÷2
=113.04(cm3)
【点睛】根据图形特点灵活运用圆柱的表面积公式和体积公式。
20.不够
【分析】根据题意,求出20毫升浓缩果汁按1∶50,可配果汁多少,再利用圆柱的体积公式求出玻璃杯的体积,再进行比较即可。
【详解】20×50=1000(毫升)
3.14×(6÷2)2×15××4
=3.14×9×(15×)×4
=28.26×10×4
=282.6×4
=1130.4(立方厘米)
=1130.4(毫升)
1000毫升<1130.4毫升
答:每人一杯不够。
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
21.282.6平方米
【分析】压路机的前轮是一个圆柱体,压路机滚动一周的压路面积等于圆柱的侧面积,根据“”表示出压路机滚动一周的压路面积,最后乘压路机每分钟转动的周数求出压路机每分钟压路的面积,据此解答。
【详解】3.14×2×3×15
=6.28×3×15
=18.84×15
=282.6(平方米)
答:压路机每分钟压路的面积是282.6平方米。
【点睛】本题主要考查圆柱侧面积公式的应用,熟记公式是解答题目的关键。
22.(1)20平方分米
(2)31.4升
(3)500秒
【分析】(1)求水桶与墙面的接触面积就是求圆柱切面的长方形面积,长方形的宽等于直径,长方形的长等于圆柱的高;
(2)这个储水桶的容积等于整个圆柱容积的一半,圆柱的容积=底面积×高,用圆柱的容积乘二分之一就是这个水桶的容积;
(3)先将水桶的单位换算成毫升,求出每秒流出水的体积,水桶的容积÷每秒流出水的体积=流水持续的时间。
【详解】(1)5×4=20(平方分米)
答:这个储水桶与墙面的接触面积有20平方分米
(2)3.14×(4÷2)2×5÷2
=3.14×20÷2
=31.4(立方分米)
=31.4(升)
答:这个储水桶最多储水31.4升。
(3)31.4升=31400毫升
3.14×(2÷2)2×20
=3.14×20
=62.8(立方厘米)
=62.8(毫升)
31400÷62.8=500(秒)
答:这桶水能持续使用500秒。
【点睛】再求这个圆柱的接触面积是要知道是求这个长方形的面积,理解长方形的宽与直径是相等的,长与圆柱的高是相等的;求水桶容积的时候重点是知道水桶的容积是圆柱容积的一半。
23.(1)厘米
(2)4.6厘米
【分析】(1)根据圆柱的体积公式:V=πr2h,据此求出水的体积,再用水的体积除以容器A的底面积即可求出容器A的水深;
(2)由题意可知,设这时水深x厘米,根据容器A的水的体积+容器B的水的体积=水的总体积,据此列方程解答即可。
【详解】(1)3.14×(20÷2)2×15÷[3.14×(30÷2)2]
=3.14×100×15÷[3.14×225]
=3.14×100×15÷706.5
=4710÷706.5
=(厘米)
答:这时容器A水深厘米。
(2)解:设这时水深x厘米。
3.14×(30÷2)2×x+3.14×(20÷2)2×x=3.14×(20÷2)2×15
3.14×225x+3.14×100x=3.14×100×15
706.5x+314x=4710
1020.5x=4710
1020.5x÷1020.5=4710÷1020.5
x≈4.6
答:这时水深4.6厘米。
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
24.0.625厘米
【分析】圆柱体积=底面积×高,图①零件的体积=高2厘米的圆柱体积+高(3-2)厘米圆柱体积的一半,图①零件的体积÷图②容器底面积=水位上升高度,据此列式解答。
【详解】2÷2=1(厘米)
3.14×12×2+3.14×12×(3-2)÷2
=3.14×1×2+3.14×1×1÷2
=6.28+1.57
=7.85(立方厘米)
7.85÷[3.14×(4÷2)2]
=7.85÷[3.14×22]
=7.85÷[3.14×4]
=7.85÷12.56
=0.625(厘米)
答:该圆柱形容器的水位将上升0.625厘米。
【点睛】关键是掌握并灵活运用圆柱体积公式。
25.226.08立方厘米
【分析】饮料瓶的底面半径和正放时饮液面的高度已知,根据圆柱的体积公式:V=,则可以求出瓶内饮料的体积,同样的方法,可以求出倒放时空余部分的体积,瓶子的容积=饮料的体积+倒放时空余部分的体积。据此解答。
【详解】3.14×32×6+3.14×32×2
=3.14×9×6+3.14×9×2
=169.56+56.52
=226.08(立方厘米)
答:这个饮料瓶的容积是226.08立方厘米。
【点睛】此题解答关键是利用体积不变的特性,把不规则图形转化为规则图形来计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
