2024 河北数学中考备考重难专题:一次函数图象与性质 课件(共34张PPT)
文档属性
| 名称 | 2024 河北数学中考备考重难专题:一次函数图象与性质 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 13:12:38 | ||
图片预览







文档简介
(共34张PPT)
河北 数学
函数图象与性质综合题
2023中考备考重难专题课件
一次函数性质综合题
一次函数性质综合题
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2022 25 解 答 题 10 (1)待定系数法求直线解析式(需设解析式,2点); (2)结合新定义光点问题考查含参一次函数问题: ①含参直线与x轴的交点坐标; ②含参直线与定线段交点问题、整点问题,分类讨论思想 (1)求直线解析式 (2)①求含参直线中,一次项系数和常数项间的数量关系; ②求整数m(一次项系数)的个数 交点为整点问题
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2020 24 解 答 题 10 (1)根据一次函数图象求直线解析式(不设解析式,2点); (2)根据一次函数解析式画图象,直线与y轴交点,两条一次函数的交点问题,两点间距离(勾股定理); (3)直线y=a与两条定直线的交点问题,中点坐标(关于某点对称),分类讨论思想 (1)求直线解析式 (2)画直线,求直线被一次函数和y轴所截的线段长 (3)求a(直线y=a)的值 三条直线三个交点问题,其中一点为另外两点的对称点
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2018 24 解 答 题 10 (1)一次函数图象上点的性质,正比例函数解析式的确定(需设解析式); (2)一次函数与坐标轴的交点坐标,两直线交点坐标,三角形面积; (3)三条直线不能构成三角形:两直线平行,三条直线过同一个交点 (1)求交点横坐标及正比例函数解析式 (2)求两三角形面积差 (3)求满足三条直线不能围成三角形的一次函数系数 三条直线不能围成三角形的情况
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2017 24 解 答 题 10 (1)直线与x轴,与另一条直线交点坐标,待定系数法求解析式(对称点的性质) (2)已知点坐标,求三角形四边形面积 (3)三角形关于x轴翻折,验证翻折前后三角形面积是否相等(利用三点共线) (1)求交点坐标及直线解析式 (2)求三角形与四边形面积和 (3)三角形翻折后,验证两三角形面积是否相等 三点共线问题
典例精讲
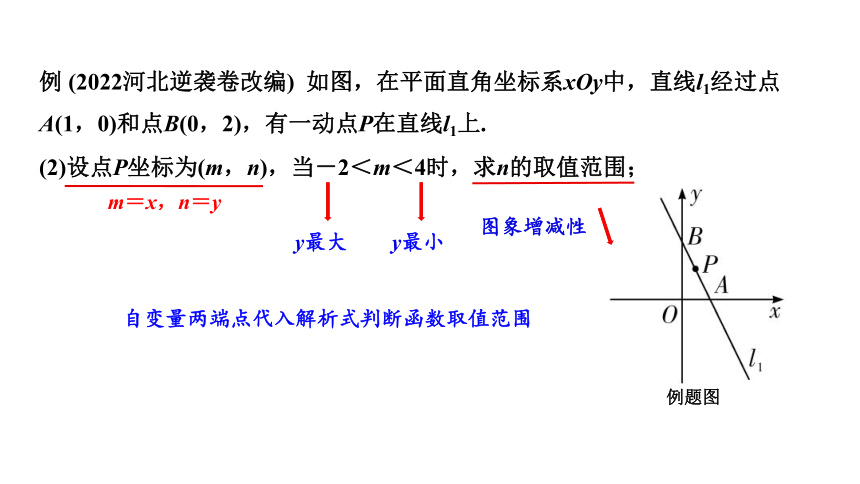
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(1)求直线l1的解析式;
看图可知系数k≠0
解:(1)设直线l1的解析式为y=kx+b(k≠0),
根据题意得,
∴直线l1的解析式为y=-2x+2;
例题图
解析式未知设y=kx+b(k≠0)
代入A、B点坐标
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(2)设点P坐标为(m,n),当-2<m<4时,求n的取值范围;
m=x,n=y
图象增减性
自变量两端点代入解析式判断函数取值范围
例题图
y最大
y最小
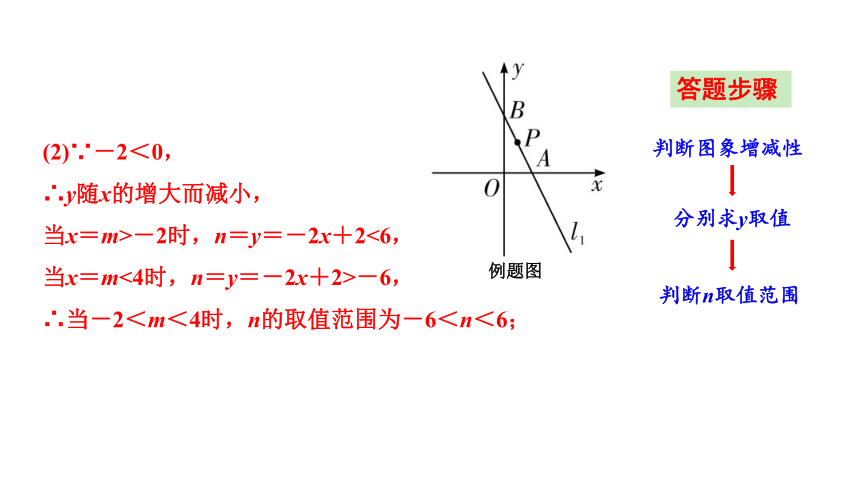
(2)∵-2<0,
∴y随x的增大而减小,
当x=m>-2时,n=y=-2x+2<6,
当x=m<4时,n=y=-2x+2>-6,
∴当-2<m<4时,n的取值范围为-6<n<6;
答题步骤
判断图象增减性
分别求y取值
判断n取值范围
例题图
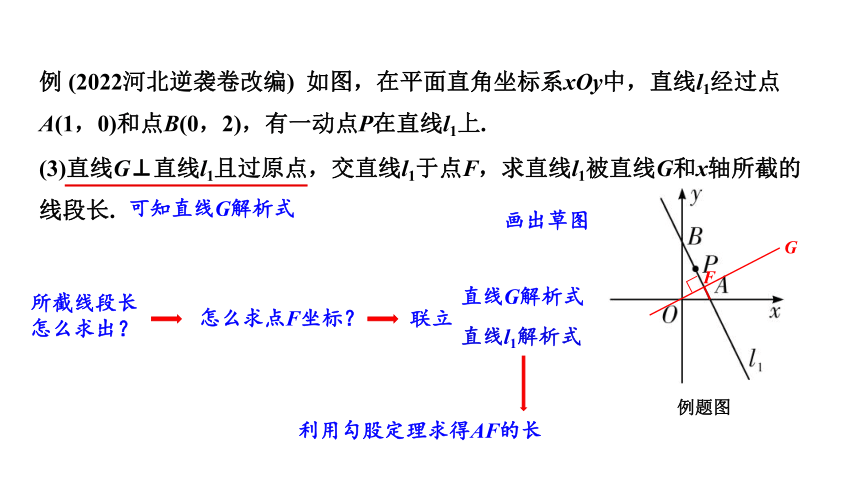
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(3)直线G⊥直线l1且过原点,交直线l1于点F,求直线l1被直线G和x轴所截的线段长.
画出草图
所截线段长怎么求出?
可知直线G解析式
F
G
∟
例题图
怎么求点F坐标?
联立
直线G解析式
直线l1解析式
利用勾股定理求得AF的长
答题步骤
设直线G解析式
求系数,得G解析式
求点F坐标
求所截线段长
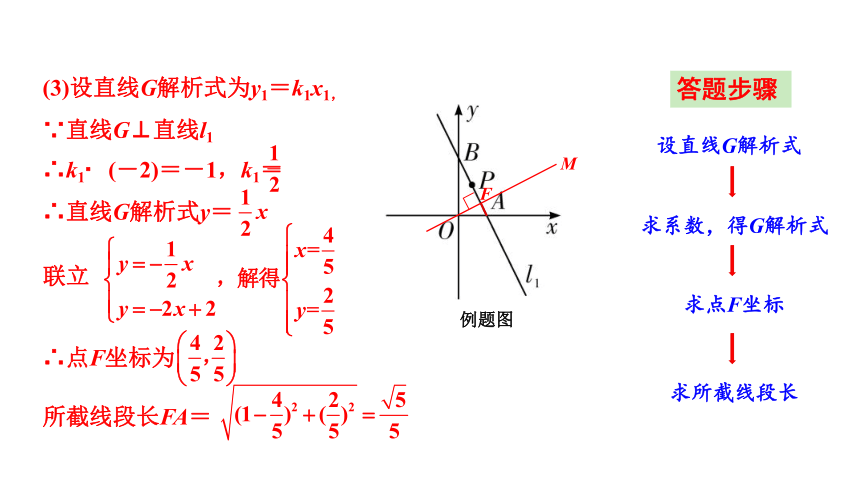
(3)设直线G解析式为y1=k1x1,
∵直线G⊥直线l1
∴k1 (-2)=-1,k1=
∴直线G解析式y=
联立
∴点F坐标为
所截线段长FA=
F
M
∟
例题图
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
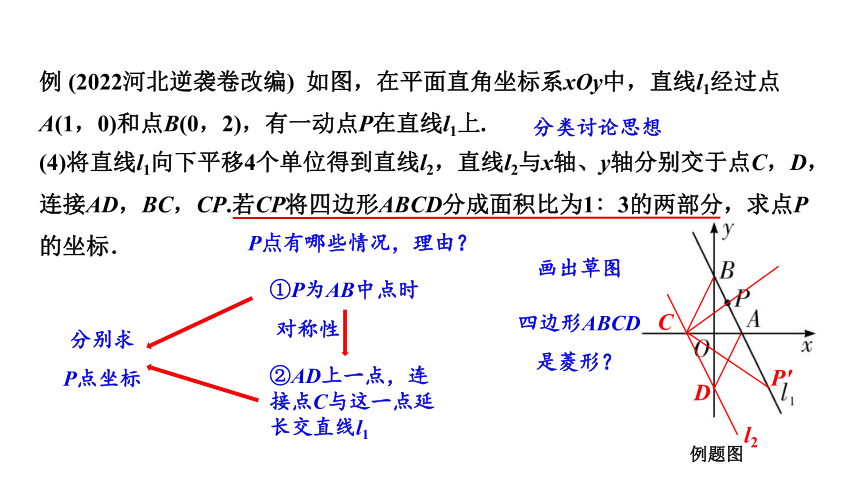
(4)将直线l1向下平移4个单位得到直线l2,直线l2与x轴、y轴分别交于点C,D,连接AD,BC,CP.若CP将四边形ABCD分成面积比为1∶3的两部分,求点P的坐标.
画出草图
四边形ABCD是菱形?
P点有哪些情况,理由?
①P为AB中点时
l2
C
D
P'
例题图
②AD上一点,连接点C与这一点延长交直线l1
对称性
分别求
P点坐标
分类讨论思想
答题步骤
求出直线l2解析式
得出C、D点坐标
证明四边形ABCD是菱形
点P为AB中点时坐标
延长线与直线l1的交点时P点坐标
(4)∵将直线l1向下平移4个单位得到直线l2,
∴直线l2的解析式为y=-2x-2.
∴当y=-2x-2=0时,解得x=-1;
当x=0时,y=-2x-2=-2.
∴C(-1,0),D(0,-2),
∴OA=OC=1,OB=OD=2.
∵OA⊥OB,∴四边形ABCD是菱形,
∴当CP过AB或AD中点时,将四边形ABCD分成面积
比为1∶3的两部分.
l2
C
D
P'
例题图
M
E
当点P为AB中点时,如图,取OA的中点E,连接PE,则PE∥y轴,
PE= OB=1
∴P( , 1 )
取AD的中点M,由对称性可知,M( , 1 )
由C,M两点坐标可求得直线CM的解析式为y=- x-
联立方程 ,∴P'(2 , -2 )
综上所述,点P的坐标为( , 1 )或P'(2 , -2 )
l2
C
D
P'
例题图
M
E
选题依据:此题考查学生运算能力、推理能力、几何直观能力
考查一次函数性质,图象,增减性,一次函数图象平移求解析式,交点中的整点坐标、线段长、面积问题
方法总结
一次函数性质综合题
知识点:
待定系数法求函数解析式、一次函数图象、增减性
与坐标轴交点坐标、平移后的解析式
直线上的点坐标特征
交点问题考查类型:
①求整点个数;②求线段长;③求面积问题
解题关键点联立两解析式求交点坐标
数学思想:
数形结合、分类讨论
课堂练兵
练习 (2022河北预测卷)如图,在平面直角坐标系中,过点A(-3,-2),B(0,4)作直线l1交x轴于点C,直线l2:y=mx+4(m≠0)与x轴交于点D.
(1)求点C的坐标;
C点是直线l1与x轴交点坐标
先求出直线l1的解析式,
令y=0求点C坐标
练习题图
解:(1)设直线l1的解析式为y=kx+b(k≠0),
依题意得
∴直线l1的解析式为y=2x+4,
令y=0,则2x+4=0,解得x=-2.
∴点C的坐标为(-2,0);
练习题图
练习 (2022河北预测卷)如图,在平面直角坐标系中,过点A(-3,-2),B(0,4)作直线l1交x轴于点C,直线l2:y=mx+4(m≠0)与x轴交于点D.
(2)若S△ACD=5,求m的值;
S△ACD底为CD,
高为A点离x轴的距离
就是求直线l2解析式,先求得D点坐标
练习题图
CD=5
D点横坐标怎么求?
CD=|Dx+2|=5
分情况代入直线l2解析式求m
S△ACD= CD×2=5
答题步骤
设D点坐标
求得CD的值
求D点坐标
代入求m的值
(2)设点D的坐标为(n,0),
∵C(-2,0),∴CD=|n+2|,
∵S△ACD=5,且点A到x轴的距离为2,
∴ CD×2=5,
∴CD=5,即|n+2|=5,∴n=3或-7,
∴点D的坐标为(3,0)或(-7,0),
∴0=3m+4或0=-7m+4,∴m=- 或 .
练习题图
练习 (2022河北预测卷)如图,在平面直角坐标系中,过点A(-3,-2),B(0,4)作直线l1交x轴于点C,直线l2:y=mx+4(m≠0)与x轴交于点D.
(3)直线y=2分别与直线l1、直线l2交于点P,Q,若PQ≥4,求m的取值范围.
练习题图
直线l2过B点
PQ是△BCD的中位线
PQ为4时,通过CD求得D点坐标
代入l1求得m的值
判断m取值范围
答题步骤
判断B点在直线l2上
证明PQ是△BCD
的中位线
求D点坐标
求m值
判断取值范围
(3)∵B(0,4),且4=0×m+4,
∴点B在直线l2:y=mx+4(m≠0)上,
∵OB=4,直线y=2分别与直线l1、
直线l2:y=mx+4(m≠0)相交于点P,Q,
∴PQ是△BCD的中位线,∴PQ= CD
当PQ=4时,CD=8,∴D(6,0)或D(-10,0),
当D(6,0)时,有0=6m+4 ,解得m=-
当D(-10,0)时,有0=-10m+4,解得m=
∵PQ≥4,∴m的取值范围为- ≤m<0或0<m≤
练习题图
解法二:已知直线l1解析式,先求出P点坐标
此时PQ距离表示为PQ=|1+xQ|≥4,求出xQ的取值xQ≥3或xQ≤5
Q点纵坐标为2,把Q点坐标代入l2解析式中,求得m
结合PQ≥4判断m的取值范围
答题步骤
求P点坐标
表示PQ距离
求出Q点坐标
求出m
判断取值范围
练习题图
课后小练
练习1 (2021河北逆袭成果卷)如图,在平面直角坐标系中,直线y1=kx+b(k≠0)交y轴于点(0,4),与直线y2= x 交于点A(4,1).将直线y2= x平移m个单位长度得到直线y3= x+m,直线y3= x+m交y轴于点B,交直线y1=kx+b(k≠0)于点C. 线段OA、OB、BC、AC围成的区域记为M(不含边界),把横、纵坐标都是整数的点称为整点.
(1)求直线y1=kx+b(k≠0)的解析式;
练习1题图
解:(1)将点(0,4)、A(4,1)代入y1=kx+b(k≠0),
∴直线y1=kx+b(k≠0)的解析式为y1=- x+4
练习1题图
(2)若m=-1,求区域M内整点的坐标;
练习1 (2021河北逆袭成果卷)如图,在平面直角坐标系中,直线y1=kx+b(k≠0)交y轴于点(0,4),与直线y2= x 交于点A(4,1).将直线y2= x平移m个单位长度得到直线y3= x+m,直线y3= x+m交y轴于点B,交直线y1=kx+b(k≠0)于点C. 线段OA、OB、BC、AC围成的区域记为M(不含边界),把横、纵坐标都是整数的点称为整点.
练习1题图
(2)当m=-1时,y3= x-1,
∴点C的坐标为(5, )
∵直线y3= x-1交y轴于点B,
∴B(0,﹣1),
∴区域M内的整点有3个,坐标为(1,0),(2,0),(3,0);
练习1题图
练习1 (2021河北逆袭成果卷)如图,在平面直角坐标系中,直线y1=kx+b(k≠0)交y轴于点(0,4),与直线y2= x 交于点A(4,1).将直线y2= x平移m个单位长度得到直线y3= x+m,直线y3= x+m交y轴于点B,交直线y1=kx+b(k≠0)于点C. 线段OA、OB、BC、AC围成的区域记为M(不含边界),把横、纵坐标都是整数的点称为整点.
(3)若区域M内恰有4个整点,结合函数图象,
直接写出m的取值范围.
练习1题图
【解法提示】可分两种情况讨论:①直线y3= x+m在OA的下方,当直线y3= x+m过(1,﹣1)时,m=﹣ ,此时区域M内有4个整点,由(2)可知,当m=﹣1时,区域M内有3个整点,∴当区域M内恰有4个整点时,m的取值范围是﹣ ≤m<﹣1;
②直线y3= x+m在OA的上方,当直线y3= x+m过(1,2)时,m= ,此时区域M内有4个整点,当直线y3= x+m过(2,2)时,m= ,此时区域M内有3个整点,∴当区域M内恰有4个整点时,m的取值范围是 <m≤ .综上所述,m的取值范围是﹣ ≤m<﹣1或 <m≤ .
(3)﹣ ≤m<﹣1或 <m≤ .
练习1题图
练习2 (2022河北预测卷)如图,一次函数y=nx+4的图象与双曲线y= (x<0)交于点A(-3,-2),点P从点O出发,沿y轴向下运动,过点P的直线y=a也随之移动,直线y=a分别交一次函数的图象和双曲线于点B,C(B与C不重合).
(1)求n,k的值;
练习2题图
解:(1)把点A(-3,-2)代入一次函数y=nx+4,
得-2=-3n+4,解得n=2.
把点A(-3,-2)代入双曲线y= (x<0),
得-2= ,解得k=6;
练习2题图
练习2 (2022河北预测卷)如图,一次函数y=nx+4的图象与双曲线y= (x<0)交于点A(-3,-2),点P从点O出发,沿y轴向下运动,过点P的直线y=a也随之移动,直线y=a分别交一次函数的图象和双曲线于点B,C(B与C不重合).
(2)若线段BC的长为2,求点P的坐标;
(2)由(1)可得一次函数解析式为y=2x+4,双曲线为y= (x<0).
∵直线y=a与一次函数y=2x+4的图象交于点B,
与双曲线y= (x<0)交于点C,
∴点B,C的纵坐标均为a,且a<0,
将y=a分别代入,得2x+4=a,
∴x= ; =a,
∴x= . ∴点B( ,a),点C( ,a).
∴线段BC的长度为 .
∵线段BC的长度为2.
∴ .
解得a1= (舍去),a2=- ,
或a1=4+ (舍去),a2=4- ,
∴点P的坐标为(0,- )或(0,4- );
练习2题图
练习2 (2022河北预测卷)如图,一次函数y=nx+4的图象与双曲线y= (x<0)交于点A(-3,-2),点P从点O出发,沿y轴向下运动,过点P的直线y=a也随之移动,直线y=a分别交一次函数的图象和双曲线于点B,C(B与C不重合).
(3)将双曲线y= (x<0)在点A,C之间的部分与线段AB,BC围成的区域(不含边界)记作G,把横、纵坐标都是整数的点叫做整点,若区域G内的整点恰好为3个,结合函数图象,直接写出a的取值范围.
练习2题图
【解法提示】如解图,∵点P的坐标为(0,a),其中a<0,若区域G内的整点恰好为3个,当直线y=a在点A的上方,点C为(-6,-1)时,a=-1,此时点B(- ,-1),此时线段BC(不包含C)上有整点(-5,-1),(-4,-1),(-3,-1),∴-1<a<0;当直线y=a在点A的下方,点B′为(-4,-4)时,a=-4,此时点C′(- ,-4),
∴线段B′C′(不包含B′)上有整点(-3,4),(-2,-4). ∵点A(-3,-2),
∴点(-3,-3)在G内部,∴-5≤a<-4.
综上所述,当-1<a<0或-5≤a<-4时,
区域G内的整点恰好为3个.
(3)-1<a<0或-5≤a<-4.
练习2解图
河北 数学
函数图象与性质综合题
2023中考备考重难专题课件
一次函数性质综合题
一次函数性质综合题
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2022 25 解 答 题 10 (1)待定系数法求直线解析式(需设解析式,2点); (2)结合新定义光点问题考查含参一次函数问题: ①含参直线与x轴的交点坐标; ②含参直线与定线段交点问题、整点问题,分类讨论思想 (1)求直线解析式 (2)①求含参直线中,一次项系数和常数项间的数量关系; ②求整数m(一次项系数)的个数 交点为整点问题
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2020 24 解 答 题 10 (1)根据一次函数图象求直线解析式(不设解析式,2点); (2)根据一次函数解析式画图象,直线与y轴交点,两条一次函数的交点问题,两点间距离(勾股定理); (3)直线y=a与两条定直线的交点问题,中点坐标(关于某点对称),分类讨论思想 (1)求直线解析式 (2)画直线,求直线被一次函数和y轴所截的线段长 (3)求a(直线y=a)的值 三条直线三个交点问题,其中一点为另外两点的对称点
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2018 24 解 答 题 10 (1)一次函数图象上点的性质,正比例函数解析式的确定(需设解析式); (2)一次函数与坐标轴的交点坐标,两直线交点坐标,三角形面积; (3)三条直线不能构成三角形:两直线平行,三条直线过同一个交点 (1)求交点横坐标及正比例函数解析式 (2)求两三角形面积差 (3)求满足三条直线不能围成三角形的一次函数系数 三条直线不能围成三角形的情况
年份 题号 题型 分值 考查内容 设问形式 探究的问题
2017 24 解 答 题 10 (1)直线与x轴,与另一条直线交点坐标,待定系数法求解析式(对称点的性质) (2)已知点坐标,求三角形四边形面积 (3)三角形关于x轴翻折,验证翻折前后三角形面积是否相等(利用三点共线) (1)求交点坐标及直线解析式 (2)求三角形与四边形面积和 (3)三角形翻折后,验证两三角形面积是否相等 三点共线问题
典例精讲
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(1)求直线l1的解析式;
看图可知系数k≠0
解:(1)设直线l1的解析式为y=kx+b(k≠0),
根据题意得,
∴直线l1的解析式为y=-2x+2;
例题图
解析式未知设y=kx+b(k≠0)
代入A、B点坐标
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(2)设点P坐标为(m,n),当-2<m<4时,求n的取值范围;
m=x,n=y
图象增减性
自变量两端点代入解析式判断函数取值范围
例题图
y最大
y最小
(2)∵-2<0,
∴y随x的增大而减小,
当x=m>-2时,n=y=-2x+2<6,
当x=m<4时,n=y=-2x+2>-6,
∴当-2<m<4时,n的取值范围为-6<n<6;
答题步骤
判断图象增减性
分别求y取值
判断n取值范围
例题图
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(3)直线G⊥直线l1且过原点,交直线l1于点F,求直线l1被直线G和x轴所截的线段长.
画出草图
所截线段长怎么求出?
可知直线G解析式
F
G
∟
例题图
怎么求点F坐标?
联立
直线G解析式
直线l1解析式
利用勾股定理求得AF的长
答题步骤
设直线G解析式
求系数,得G解析式
求点F坐标
求所截线段长
(3)设直线G解析式为y1=k1x1,
∵直线G⊥直线l1
∴k1 (-2)=-1,k1=
∴直线G解析式y=
联立
∴点F坐标为
所截线段长FA=
F
M
∟
例题图
例 (2022河北逆袭卷改编) 如图,在平面直角坐标系xOy中,直线l1经过点 A(1,0)和点B(0,2),有一动点P在直线l1上.
(4)将直线l1向下平移4个单位得到直线l2,直线l2与x轴、y轴分别交于点C,D,连接AD,BC,CP.若CP将四边形ABCD分成面积比为1∶3的两部分,求点P的坐标.
画出草图
四边形ABCD是菱形?
P点有哪些情况,理由?
①P为AB中点时
l2
C
D
P'
例题图
②AD上一点,连接点C与这一点延长交直线l1
对称性
分别求
P点坐标
分类讨论思想
答题步骤
求出直线l2解析式
得出C、D点坐标
证明四边形ABCD是菱形
点P为AB中点时坐标
延长线与直线l1的交点时P点坐标
(4)∵将直线l1向下平移4个单位得到直线l2,
∴直线l2的解析式为y=-2x-2.
∴当y=-2x-2=0时,解得x=-1;
当x=0时,y=-2x-2=-2.
∴C(-1,0),D(0,-2),
∴OA=OC=1,OB=OD=2.
∵OA⊥OB,∴四边形ABCD是菱形,
∴当CP过AB或AD中点时,将四边形ABCD分成面积
比为1∶3的两部分.
l2
C
D
P'
例题图
M
E
当点P为AB中点时,如图,取OA的中点E,连接PE,则PE∥y轴,
PE= OB=1
∴P( , 1 )
取AD的中点M,由对称性可知,M( , 1 )
由C,M两点坐标可求得直线CM的解析式为y=- x-
联立方程 ,∴P'(2 , -2 )
综上所述,点P的坐标为( , 1 )或P'(2 , -2 )
l2
C
D
P'
例题图
M
E
选题依据:此题考查学生运算能力、推理能力、几何直观能力
考查一次函数性质,图象,增减性,一次函数图象平移求解析式,交点中的整点坐标、线段长、面积问题
方法总结
一次函数性质综合题
知识点:
待定系数法求函数解析式、一次函数图象、增减性
与坐标轴交点坐标、平移后的解析式
直线上的点坐标特征
交点问题考查类型:
①求整点个数;②求线段长;③求面积问题
解题关键点联立两解析式求交点坐标
数学思想:
数形结合、分类讨论
课堂练兵
练习 (2022河北预测卷)如图,在平面直角坐标系中,过点A(-3,-2),B(0,4)作直线l1交x轴于点C,直线l2:y=mx+4(m≠0)与x轴交于点D.
(1)求点C的坐标;
C点是直线l1与x轴交点坐标
先求出直线l1的解析式,
令y=0求点C坐标
练习题图
解:(1)设直线l1的解析式为y=kx+b(k≠0),
依题意得
∴直线l1的解析式为y=2x+4,
令y=0,则2x+4=0,解得x=-2.
∴点C的坐标为(-2,0);
练习题图
练习 (2022河北预测卷)如图,在平面直角坐标系中,过点A(-3,-2),B(0,4)作直线l1交x轴于点C,直线l2:y=mx+4(m≠0)与x轴交于点D.
(2)若S△ACD=5,求m的值;
S△ACD底为CD,
高为A点离x轴的距离
就是求直线l2解析式,先求得D点坐标
练习题图
CD=5
D点横坐标怎么求?
CD=|Dx+2|=5
分情况代入直线l2解析式求m
S△ACD= CD×2=5
答题步骤
设D点坐标
求得CD的值
求D点坐标
代入求m的值
(2)设点D的坐标为(n,0),
∵C(-2,0),∴CD=|n+2|,
∵S△ACD=5,且点A到x轴的距离为2,
∴ CD×2=5,
∴CD=5,即|n+2|=5,∴n=3或-7,
∴点D的坐标为(3,0)或(-7,0),
∴0=3m+4或0=-7m+4,∴m=- 或 .
练习题图
练习 (2022河北预测卷)如图,在平面直角坐标系中,过点A(-3,-2),B(0,4)作直线l1交x轴于点C,直线l2:y=mx+4(m≠0)与x轴交于点D.
(3)直线y=2分别与直线l1、直线l2交于点P,Q,若PQ≥4,求m的取值范围.
练习题图
直线l2过B点
PQ是△BCD的中位线
PQ为4时,通过CD求得D点坐标
代入l1求得m的值
判断m取值范围
答题步骤
判断B点在直线l2上
证明PQ是△BCD
的中位线
求D点坐标
求m值
判断取值范围
(3)∵B(0,4),且4=0×m+4,
∴点B在直线l2:y=mx+4(m≠0)上,
∵OB=4,直线y=2分别与直线l1、
直线l2:y=mx+4(m≠0)相交于点P,Q,
∴PQ是△BCD的中位线,∴PQ= CD
当PQ=4时,CD=8,∴D(6,0)或D(-10,0),
当D(6,0)时,有0=6m+4 ,解得m=-
当D(-10,0)时,有0=-10m+4,解得m=
∵PQ≥4,∴m的取值范围为- ≤m<0或0<m≤
练习题图
解法二:已知直线l1解析式,先求出P点坐标
此时PQ距离表示为PQ=|1+xQ|≥4,求出xQ的取值xQ≥3或xQ≤5
Q点纵坐标为2,把Q点坐标代入l2解析式中,求得m
结合PQ≥4判断m的取值范围
答题步骤
求P点坐标
表示PQ距离
求出Q点坐标
求出m
判断取值范围
练习题图
课后小练
练习1 (2021河北逆袭成果卷)如图,在平面直角坐标系中,直线y1=kx+b(k≠0)交y轴于点(0,4),与直线y2= x 交于点A(4,1).将直线y2= x平移m个单位长度得到直线y3= x+m,直线y3= x+m交y轴于点B,交直线y1=kx+b(k≠0)于点C. 线段OA、OB、BC、AC围成的区域记为M(不含边界),把横、纵坐标都是整数的点称为整点.
(1)求直线y1=kx+b(k≠0)的解析式;
练习1题图
解:(1)将点(0,4)、A(4,1)代入y1=kx+b(k≠0),
∴直线y1=kx+b(k≠0)的解析式为y1=- x+4
练习1题图
(2)若m=-1,求区域M内整点的坐标;
练习1 (2021河北逆袭成果卷)如图,在平面直角坐标系中,直线y1=kx+b(k≠0)交y轴于点(0,4),与直线y2= x 交于点A(4,1).将直线y2= x平移m个单位长度得到直线y3= x+m,直线y3= x+m交y轴于点B,交直线y1=kx+b(k≠0)于点C. 线段OA、OB、BC、AC围成的区域记为M(不含边界),把横、纵坐标都是整数的点称为整点.
练习1题图
(2)当m=-1时,y3= x-1,
∴点C的坐标为(5, )
∵直线y3= x-1交y轴于点B,
∴B(0,﹣1),
∴区域M内的整点有3个,坐标为(1,0),(2,0),(3,0);
练习1题图
练习1 (2021河北逆袭成果卷)如图,在平面直角坐标系中,直线y1=kx+b(k≠0)交y轴于点(0,4),与直线y2= x 交于点A(4,1).将直线y2= x平移m个单位长度得到直线y3= x+m,直线y3= x+m交y轴于点B,交直线y1=kx+b(k≠0)于点C. 线段OA、OB、BC、AC围成的区域记为M(不含边界),把横、纵坐标都是整数的点称为整点.
(3)若区域M内恰有4个整点,结合函数图象,
直接写出m的取值范围.
练习1题图
【解法提示】可分两种情况讨论:①直线y3= x+m在OA的下方,当直线y3= x+m过(1,﹣1)时,m=﹣ ,此时区域M内有4个整点,由(2)可知,当m=﹣1时,区域M内有3个整点,∴当区域M内恰有4个整点时,m的取值范围是﹣ ≤m<﹣1;
②直线y3= x+m在OA的上方,当直线y3= x+m过(1,2)时,m= ,此时区域M内有4个整点,当直线y3= x+m过(2,2)时,m= ,此时区域M内有3个整点,∴当区域M内恰有4个整点时,m的取值范围是 <m≤ .综上所述,m的取值范围是﹣ ≤m<﹣1或 <m≤ .
(3)﹣ ≤m<﹣1或 <m≤ .
练习1题图
练习2 (2022河北预测卷)如图,一次函数y=nx+4的图象与双曲线y= (x<0)交于点A(-3,-2),点P从点O出发,沿y轴向下运动,过点P的直线y=a也随之移动,直线y=a分别交一次函数的图象和双曲线于点B,C(B与C不重合).
(1)求n,k的值;
练习2题图
解:(1)把点A(-3,-2)代入一次函数y=nx+4,
得-2=-3n+4,解得n=2.
把点A(-3,-2)代入双曲线y= (x<0),
得-2= ,解得k=6;
练习2题图
练习2 (2022河北预测卷)如图,一次函数y=nx+4的图象与双曲线y= (x<0)交于点A(-3,-2),点P从点O出发,沿y轴向下运动,过点P的直线y=a也随之移动,直线y=a分别交一次函数的图象和双曲线于点B,C(B与C不重合).
(2)若线段BC的长为2,求点P的坐标;
(2)由(1)可得一次函数解析式为y=2x+4,双曲线为y= (x<0).
∵直线y=a与一次函数y=2x+4的图象交于点B,
与双曲线y= (x<0)交于点C,
∴点B,C的纵坐标均为a,且a<0,
将y=a分别代入,得2x+4=a,
∴x= ; =a,
∴x= . ∴点B( ,a),点C( ,a).
∴线段BC的长度为 .
∵线段BC的长度为2.
∴ .
解得a1= (舍去),a2=- ,
或a1=4+ (舍去),a2=4- ,
∴点P的坐标为(0,- )或(0,4- );
练习2题图
练习2 (2022河北预测卷)如图,一次函数y=nx+4的图象与双曲线y= (x<0)交于点A(-3,-2),点P从点O出发,沿y轴向下运动,过点P的直线y=a也随之移动,直线y=a分别交一次函数的图象和双曲线于点B,C(B与C不重合).
(3)将双曲线y= (x<0)在点A,C之间的部分与线段AB,BC围成的区域(不含边界)记作G,把横、纵坐标都是整数的点叫做整点,若区域G内的整点恰好为3个,结合函数图象,直接写出a的取值范围.
练习2题图
【解法提示】如解图,∵点P的坐标为(0,a),其中a<0,若区域G内的整点恰好为3个,当直线y=a在点A的上方,点C为(-6,-1)时,a=-1,此时点B(- ,-1),此时线段BC(不包含C)上有整点(-5,-1),(-4,-1),(-3,-1),∴-1<a<0;当直线y=a在点A的下方,点B′为(-4,-4)时,a=-4,此时点C′(- ,-4),
∴线段B′C′(不包含B′)上有整点(-3,4),(-2,-4). ∵点A(-3,-2),
∴点(-3,-3)在G内部,∴-5≤a<-4.
综上所述,当-1<a<0或-5≤a<-4时,
区域G内的整点恰好为3个.
(3)-1<a<0或-5≤a<-4.
练习2解图
同课章节目录
