2024陕西数学中考备考重难专题:抛物线型实际应用课件 23张PPT
文档属性
| 名称 | 2024陕西数学中考备考重难专题:抛物线型实际应用课件 23张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
陕西 数学
抛物线型实际应用
2024中考备考重难专题课件
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
抛物线型实际应用
课堂练兵
课后小练
1
典例精讲
2
3
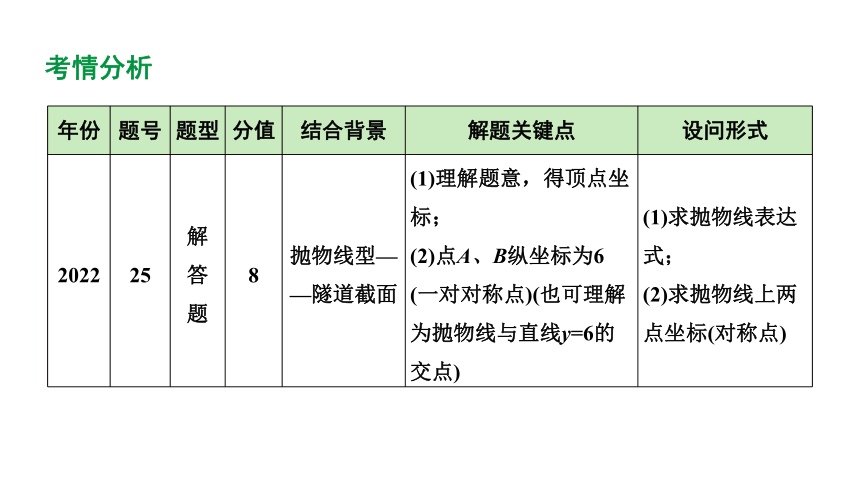
考情分析
年份 题号 题型 分值 结合背景 解题关键点 设问形式
2022 25 解 答 题 8 抛物线型——隧道截面 (1)理解题意,得顶点坐标; (2)点A、B纵坐标为6 (一对对称点)(也可理解为抛物线与直线y=6的交点) (1)求抛物线表达式;
(2)求抛物线上两点坐标(对称点)
典例精讲
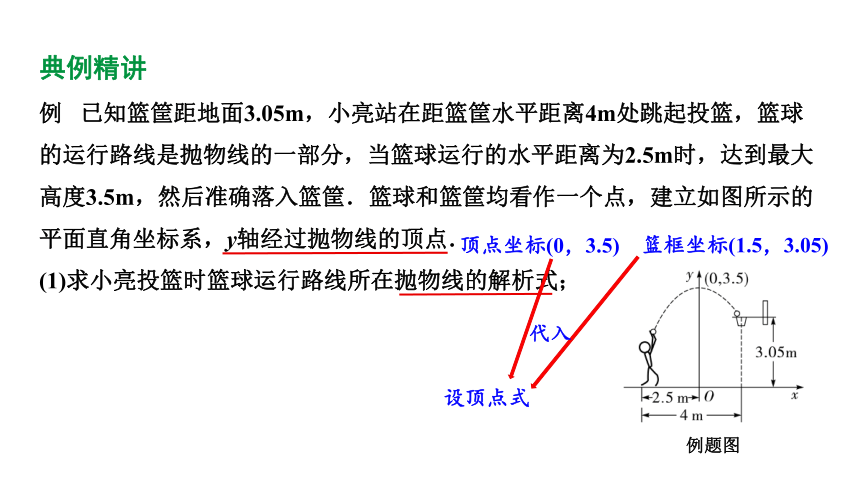
例 已知篮筐距地面3.05m,小亮站在距篮筐水平距离4m处跳起投篮,篮球的运行路线是抛物线的一部分,当篮球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐.篮球和篮筐均看作一个点,建立如图所示的平面直角坐标系,y轴经过抛物线的顶点.
(1)求小亮投篮时篮球运行路线所在抛物线的解析式;
篮框坐标(1.5,3.05)
设顶点式
例题图
顶点坐标(0,3.5)
代入
解:(1)∵抛物线的顶点在y轴上,
∴该抛物线的对称轴是y轴,
∴设抛物线解析式为y=ax2+3.5(a≠0),
∵小亮距y轴的水平距离为2.5m,距篮筐水平距离为4m,
∴篮筐距y轴的水平距离为4-2.5=1.5m,
∴篮筐的坐标为(1.5,3.05),
把(1.5,3.05)代入抛物线解析式,
得3.05=a×1.52+3.5,解得a=-0.2,
∴篮球运行路线所在抛物线的解析式为y=-0.2x2+3.5(-2.5≤x≤1.5);
例题图
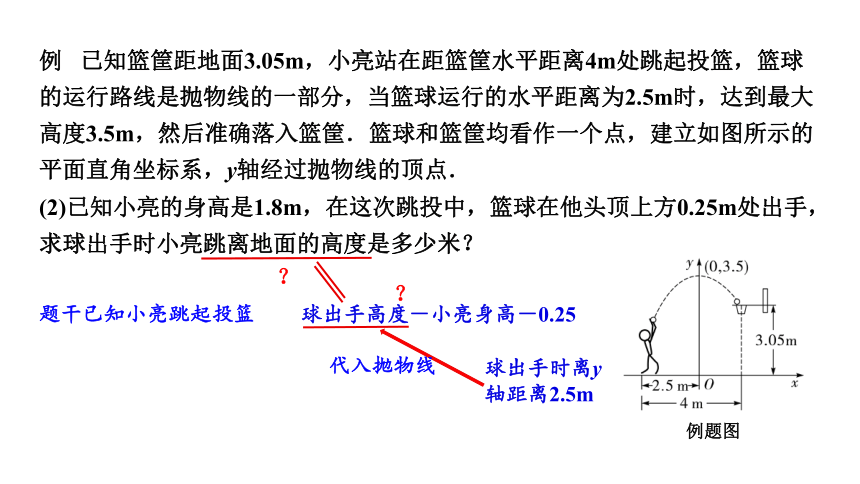
例 已知篮筐距地面3.05m,小亮站在距篮筐水平距离4m处跳起投篮,篮球的运行路线是抛物线的一部分,当篮球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐.篮球和篮筐均看作一个点,建立如图所示的平面直角坐标系,y轴经过抛物线的顶点.
(2)已知小亮的身高是1.8m,在这次跳投中,篮球在他头顶上方0.25m处出手,求球出手时小亮跳离地面的高度是多少米?
例题图
?
题干已知小亮跳起投篮
球出手高度-小亮身高-0.25
?
球出手时离y轴距离2.5m
代入抛物线
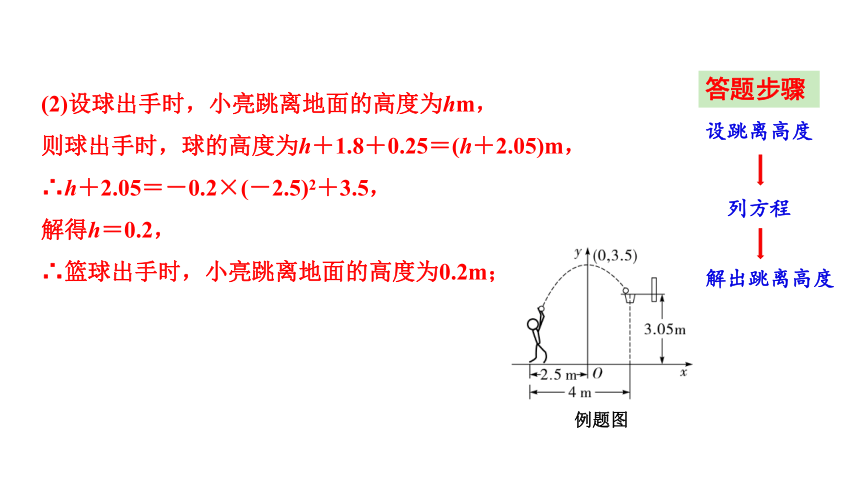
(2)设球出手时,小亮跳离地面的高度为hm,
则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,
∴h+2.05=-0.2×(-2.5)2+3.5,
解得h=0.2,
∴篮球出手时,小亮跳离地面的高度为0.2m;
例题图
答题步骤
设跳离高度
列方程
解出跳离高度
(3)若小亮投篮后篮球被篮筐弹了出来,恰被距篮筐水平距离为5m处的小明跳起来接住,小明接球的高度为2.3m.已知篮球弹出后运行路线也是抛物线的一部分(两抛物线在同一平面内),运行的水平距离为2m时到达最高点.若小明不接球,让篮球自由落地,则落地点到篮筐的水平距离是多少m
例题图
篮框坐标(1.5,3.05)
弹出抛物线过篮框
接球点坐标(-3.5,2.3)
1.5
篮筐距离y轴1.5m,篮球向x轴负半轴弹出,此时篮球坐标在第二象限距y轴距离0.5,对称轴x=-0.5
弹出抛物线与x轴交点,落地点到篮筐水平距离即:交点横坐标+篮筐到y轴水平距离1.5
信息梳理完,
怎么求解?
先求弹出抛物线,令y=0求出交点
注意:投篮背景下,篮球弹出方向只考虑小亮方向,不考虑篮筐背后方向
(3)∵篮球弹出后运行的水平距离为2 m时到达最大高度,篮筐到y轴的距离为1.5 m,
∴篮球弹出后运行路线所在抛物线的对称轴是直线x=1.5-2=-0.5,
∴设该抛物线的解析式为y=a′(x+0.5)2+k,
∵小明到篮筐的水平距离为5 m,
∴小明距y轴的水平距离为3.5 m,
∴抛物线经过点(-3.5,2.3),(1.5,3.05),
答题步骤
设抛物线解析式
点坐标代入求解析式
求出抛物线与x轴交点坐标
例题图
篮框坐标(1.5,3.05)
1.5
求水平距离
代入抛物线解析式可得, 解得 ,
∴抛物线的解析式为y=-0.15(x+0.5)2+3.65,
令-0.15(x+0.5)2+3.65=0,
解得x1=- -0.5,x2= -0.5(舍去),
∴篮球落地点距y轴( +0.5)m,
+0.5+1.5=( +2)m,
∴若小明不接球,则篮球落地点到篮筐的水平距离为( +2)m.
例题图
篮框坐标(1.5,3.05)
1.5
抛物线型实际应用题解题关键点是理解题意,从题干中梳理信息,把实际情境下的数字信息转化为数学问题,借助函数图象解决.
课堂练兵
练习 (2022宁夏真题卷)2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米.以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3∶4(即 ).
求:(1)点A的坐标;
解:(1)点A的坐标为(0,4);
练习题图
练习 (2022宁夏真题卷)2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米.以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3∶4(即 ).
(2)该抛物线的函数表达式;
A(0,4)
设顶点式,点A的坐标代入即可
练习题图
(2)∵抛物线最高点B的坐标为(4,12),
∴点B是抛物线顶点,抛物线可设为y=a(x-4)2+12(a≠0),
把点(0,4)代入得a(0-4)2+12=4,解得a=- ,
∴该抛物线的函数表达式为y=- (x-4)2+12,
即y=- x2+4x+4;
练习题图
练习 (2022宁夏真题卷)2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米.以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3∶4(即 ).
(3)起跳点A与着陆坡顶端C之间的水平距离OC的长.(精确到0.1米)
(参考数据: ≈1.73)
在函数问题中,求线段长实际上是求点坐标
直接求C点坐标可以吗?
不能
怎么求C点坐标?
求出点D的坐标(在抛物线上),再求出DE长(在直角三角形中)
练习题图
答题步骤
求DE、CE
代入求xD
计算出OC
(3)在Rt△CDE中,∵ ; ∴设CE=3x,则DE=4x,
由勾股定理得CD=5x=2.5,解得x=0.5,
∴CE=1.5,DE=2,∴点D的纵坐标为-1.5,
将yD=-1.5代入抛物线y=- (x-4)2+12,
得- (xD-4)2+12=-1.5,
解得xD=4+3 或4-3 (舍去),
∴OC=xD-ED=4+3 -2=2+3 ≈7.2(米).
∴起跳点A与着陆坡顶端C之间的水平距离OC的长约为7.2米.
练习题图
课后小练
练习1 夏天,为了防止蚊虫污染饭菜,爷爷用细竹篾编了一个罩子保护饭菜(如图①).它的横截面可以看成一个抛物线的形状.壮壮测得菜罩的跨度为80厘米,高度为32厘米,壮壮就以菜罩左边缘为原点建立平面直角坐标系(如图②).
(1)求抛物线的解析式;
练习1题图
解:(1)设抛物线解析式为y=a(x-h)2+k,
由题意知,其顶点坐标为(40,32),
则抛物线为y=a(x-40)2+32,
把点(80,0)代入,得0=a(80-40)2+32,解得a=- .
∴抛物线的解析式为y=- (x-40)2+32;
练习1题图
(2)壮壮的妈妈想购买一批直径为24厘米,高度为2.5厘米的盘子,要使菜罩紧贴桌面,菜罩内一排能放下三个这样的盘子吗?请说明理由.
练习1 夏天,为了防止蚊虫污染饭菜,爷爷用细竹篾编了一个罩子保护饭菜(如图①).它的横截面可以看成一个抛物线的形状.壮壮测得菜罩的跨度为80厘米,高度为32厘米,壮壮就以菜罩左边缘为原点建立平面直角坐标系(如图②).
(2)能放下.理由如下:
当x= =4时,
y=- ×(4-40)2+32=6.08>2.5.
∴菜罩内一排能放下三个这样的盘子.
练习1题图
练习2 某游乐园计划在道路AB上方搭建一座抛物线型彩虹桥,已知道路AB的宽为40米,桥面最高处C点距离路面的距离OC为8米.若以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系如图所示.
练习2题图
(1)求这座彩虹桥的函数解析式,并注明自变量x的取值范围;
解:(1)∵AB=40,∴OB=20.
设抛物线的解析式为y=ax2+c,
又∵抛物线经过点C(0,8)和点B(20,0),
∴抛物线的解析式为y=-0.02x2+8(-20≤x≤20);
练习2 某游乐园计划在道路AB上方搭建一座抛物线型彩虹桥,已知道路AB的宽为40米,桥面最高处C点距离路面的距离OC为8米.若以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系如图所示.
(2)按计划在该彩虹桥下方需对称安置两个桥墩进行支撑,若要保障道路AB的正常通行,两个桥墩之间的距离至少需要30米,求桥墩的最大高度(不考虑桥墩的宽度);
练习2题图
(2)∵两个桥墩之间的距离至少为30米,且对称安置,
∴桥墩距离中心OC的距离至少为15米.
令x=15,得y=-0.02×152+8=3.5,
∴桥墩的最大高度3.5米;
练习2 某游乐园计划在道路AB上方搭建一座抛物线型彩虹桥,已知道路AB的宽为40米,桥面最高处C点距离路面的距离OC为8米.若以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系如图所示.
(3)若在该彩虹桥下方有一个限高4米的横杆,现要在横杆上方设置一个宽18米,高2米的广告牌,问:在不超出桥面的情况下,这个广告牌能否按计划设置(不考虑横栏的宽度)
练习2题图
(3)由题意可得,广告牌的最高处距离路面的距离为4+2=6米.
令y=6,则-0.02x2+8=6,解得x1=-10,x2=10,
∴距离路面的距离为6米时桥面的宽度为20米.
∵18<20,∴这个广告牌能按计划设置.
陕西 数学
抛物线型实际应用
2024中考备考重难专题课件
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
抛物线型实际应用
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 结合背景 解题关键点 设问形式
2022 25 解 答 题 8 抛物线型——隧道截面 (1)理解题意,得顶点坐标; (2)点A、B纵坐标为6 (一对对称点)(也可理解为抛物线与直线y=6的交点) (1)求抛物线表达式;
(2)求抛物线上两点坐标(对称点)
典例精讲
例 已知篮筐距地面3.05m,小亮站在距篮筐水平距离4m处跳起投篮,篮球的运行路线是抛物线的一部分,当篮球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐.篮球和篮筐均看作一个点,建立如图所示的平面直角坐标系,y轴经过抛物线的顶点.
(1)求小亮投篮时篮球运行路线所在抛物线的解析式;
篮框坐标(1.5,3.05)
设顶点式
例题图
顶点坐标(0,3.5)
代入
解:(1)∵抛物线的顶点在y轴上,
∴该抛物线的对称轴是y轴,
∴设抛物线解析式为y=ax2+3.5(a≠0),
∵小亮距y轴的水平距离为2.5m,距篮筐水平距离为4m,
∴篮筐距y轴的水平距离为4-2.5=1.5m,
∴篮筐的坐标为(1.5,3.05),
把(1.5,3.05)代入抛物线解析式,
得3.05=a×1.52+3.5,解得a=-0.2,
∴篮球运行路线所在抛物线的解析式为y=-0.2x2+3.5(-2.5≤x≤1.5);
例题图
例 已知篮筐距地面3.05m,小亮站在距篮筐水平距离4m处跳起投篮,篮球的运行路线是抛物线的一部分,当篮球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐.篮球和篮筐均看作一个点,建立如图所示的平面直角坐标系,y轴经过抛物线的顶点.
(2)已知小亮的身高是1.8m,在这次跳投中,篮球在他头顶上方0.25m处出手,求球出手时小亮跳离地面的高度是多少米?
例题图
?
题干已知小亮跳起投篮
球出手高度-小亮身高-0.25
?
球出手时离y轴距离2.5m
代入抛物线
(2)设球出手时,小亮跳离地面的高度为hm,
则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,
∴h+2.05=-0.2×(-2.5)2+3.5,
解得h=0.2,
∴篮球出手时,小亮跳离地面的高度为0.2m;
例题图
答题步骤
设跳离高度
列方程
解出跳离高度
(3)若小亮投篮后篮球被篮筐弹了出来,恰被距篮筐水平距离为5m处的小明跳起来接住,小明接球的高度为2.3m.已知篮球弹出后运行路线也是抛物线的一部分(两抛物线在同一平面内),运行的水平距离为2m时到达最高点.若小明不接球,让篮球自由落地,则落地点到篮筐的水平距离是多少m
例题图
篮框坐标(1.5,3.05)
弹出抛物线过篮框
接球点坐标(-3.5,2.3)
1.5
篮筐距离y轴1.5m,篮球向x轴负半轴弹出,此时篮球坐标在第二象限距y轴距离0.5,对称轴x=-0.5
弹出抛物线与x轴交点,落地点到篮筐水平距离即:交点横坐标+篮筐到y轴水平距离1.5
信息梳理完,
怎么求解?
先求弹出抛物线,令y=0求出交点
注意:投篮背景下,篮球弹出方向只考虑小亮方向,不考虑篮筐背后方向
(3)∵篮球弹出后运行的水平距离为2 m时到达最大高度,篮筐到y轴的距离为1.5 m,
∴篮球弹出后运行路线所在抛物线的对称轴是直线x=1.5-2=-0.5,
∴设该抛物线的解析式为y=a′(x+0.5)2+k,
∵小明到篮筐的水平距离为5 m,
∴小明距y轴的水平距离为3.5 m,
∴抛物线经过点(-3.5,2.3),(1.5,3.05),
答题步骤
设抛物线解析式
点坐标代入求解析式
求出抛物线与x轴交点坐标
例题图
篮框坐标(1.5,3.05)
1.5
求水平距离
代入抛物线解析式可得, 解得 ,
∴抛物线的解析式为y=-0.15(x+0.5)2+3.65,
令-0.15(x+0.5)2+3.65=0,
解得x1=- -0.5,x2= -0.5(舍去),
∴篮球落地点距y轴( +0.5)m,
+0.5+1.5=( +2)m,
∴若小明不接球,则篮球落地点到篮筐的水平距离为( +2)m.
例题图
篮框坐标(1.5,3.05)
1.5
抛物线型实际应用题解题关键点是理解题意,从题干中梳理信息,把实际情境下的数字信息转化为数学问题,借助函数图象解决.
课堂练兵
练习 (2022宁夏真题卷)2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米.以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3∶4(即 ).
求:(1)点A的坐标;
解:(1)点A的坐标为(0,4);
练习题图
练习 (2022宁夏真题卷)2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米.以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3∶4(即 ).
(2)该抛物线的函数表达式;
A(0,4)
设顶点式,点A的坐标代入即可
练习题图
(2)∵抛物线最高点B的坐标为(4,12),
∴点B是抛物线顶点,抛物线可设为y=a(x-4)2+12(a≠0),
把点(0,4)代入得a(0-4)2+12=4,解得a=- ,
∴该抛物线的函数表达式为y=- (x-4)2+12,
即y=- x2+4x+4;
练习题图
练习 (2022宁夏真题卷)2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米.以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3∶4(即 ).
(3)起跳点A与着陆坡顶端C之间的水平距离OC的长.(精确到0.1米)
(参考数据: ≈1.73)
在函数问题中,求线段长实际上是求点坐标
直接求C点坐标可以吗?
不能
怎么求C点坐标?
求出点D的坐标(在抛物线上),再求出DE长(在直角三角形中)
练习题图
答题步骤
求DE、CE
代入求xD
计算出OC
(3)在Rt△CDE中,∵ ; ∴设CE=3x,则DE=4x,
由勾股定理得CD=5x=2.5,解得x=0.5,
∴CE=1.5,DE=2,∴点D的纵坐标为-1.5,
将yD=-1.5代入抛物线y=- (x-4)2+12,
得- (xD-4)2+12=-1.5,
解得xD=4+3 或4-3 (舍去),
∴OC=xD-ED=4+3 -2=2+3 ≈7.2(米).
∴起跳点A与着陆坡顶端C之间的水平距离OC的长约为7.2米.
练习题图
课后小练
练习1 夏天,为了防止蚊虫污染饭菜,爷爷用细竹篾编了一个罩子保护饭菜(如图①).它的横截面可以看成一个抛物线的形状.壮壮测得菜罩的跨度为80厘米,高度为32厘米,壮壮就以菜罩左边缘为原点建立平面直角坐标系(如图②).
(1)求抛物线的解析式;
练习1题图
解:(1)设抛物线解析式为y=a(x-h)2+k,
由题意知,其顶点坐标为(40,32),
则抛物线为y=a(x-40)2+32,
把点(80,0)代入,得0=a(80-40)2+32,解得a=- .
∴抛物线的解析式为y=- (x-40)2+32;
练习1题图
(2)壮壮的妈妈想购买一批直径为24厘米,高度为2.5厘米的盘子,要使菜罩紧贴桌面,菜罩内一排能放下三个这样的盘子吗?请说明理由.
练习1 夏天,为了防止蚊虫污染饭菜,爷爷用细竹篾编了一个罩子保护饭菜(如图①).它的横截面可以看成一个抛物线的形状.壮壮测得菜罩的跨度为80厘米,高度为32厘米,壮壮就以菜罩左边缘为原点建立平面直角坐标系(如图②).
(2)能放下.理由如下:
当x= =4时,
y=- ×(4-40)2+32=6.08>2.5.
∴菜罩内一排能放下三个这样的盘子.
练习1题图
练习2 某游乐园计划在道路AB上方搭建一座抛物线型彩虹桥,已知道路AB的宽为40米,桥面最高处C点距离路面的距离OC为8米.若以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系如图所示.
练习2题图
(1)求这座彩虹桥的函数解析式,并注明自变量x的取值范围;
解:(1)∵AB=40,∴OB=20.
设抛物线的解析式为y=ax2+c,
又∵抛物线经过点C(0,8)和点B(20,0),
∴抛物线的解析式为y=-0.02x2+8(-20≤x≤20);
练习2 某游乐园计划在道路AB上方搭建一座抛物线型彩虹桥,已知道路AB的宽为40米,桥面最高处C点距离路面的距离OC为8米.若以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系如图所示.
(2)按计划在该彩虹桥下方需对称安置两个桥墩进行支撑,若要保障道路AB的正常通行,两个桥墩之间的距离至少需要30米,求桥墩的最大高度(不考虑桥墩的宽度);
练习2题图
(2)∵两个桥墩之间的距离至少为30米,且对称安置,
∴桥墩距离中心OC的距离至少为15米.
令x=15,得y=-0.02×152+8=3.5,
∴桥墩的最大高度3.5米;
练习2 某游乐园计划在道路AB上方搭建一座抛物线型彩虹桥,已知道路AB的宽为40米,桥面最高处C点距离路面的距离OC为8米.若以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系如图所示.
(3)若在该彩虹桥下方有一个限高4米的横杆,现要在横杆上方设置一个宽18米,高2米的广告牌,问:在不超出桥面的情况下,这个广告牌能否按计划设置(不考虑横栏的宽度)
练习2题图
(3)由题意可得,广告牌的最高处距离路面的距离为4+2=6米.
令y=6,则-0.02x2+8=6,解得x1=-10,x2=10,
∴距离路面的距离为6米时桥面的宽度为20米.
∵18<20,∴这个广告牌能按计划设置.
同课章节目录
