2024陕西数学中考备考重难专题:抛物线与几何综合题线段、面积问题课件 30张PPT
文档属性
| 名称 | 2024陕西数学中考备考重难专题:抛物线与几何综合题线段、面积问题课件 30张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 14:23:24 | ||
图片预览




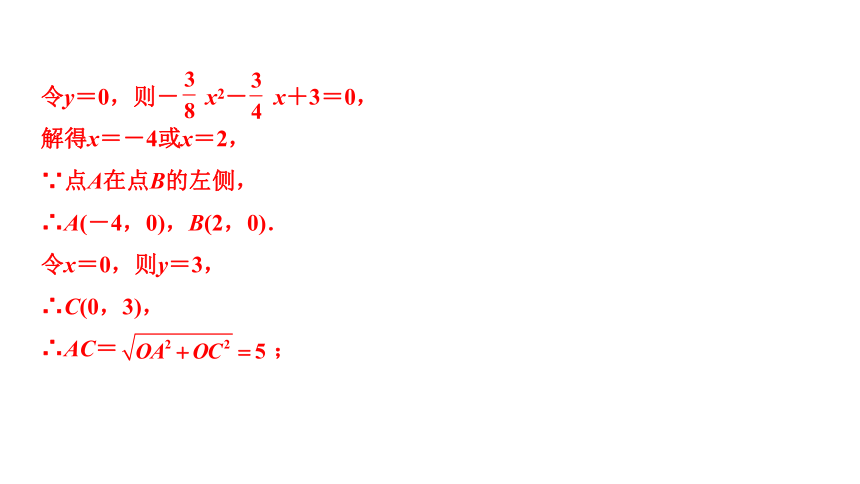



文档简介
(共30张PPT)
陕西 数学
抛物线与几何综合题
2024中考备考重难专题课件
线段、面积问题
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
抛物线与几何综合题
线段、面积问题
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 抛物线变化情况 设问形式 解题关键点
2018 24 解 答 题 10 平移 (1)求抛物线与坐标轴交点坐标及交点为顶点的三角形面积 (2)求满足面积等量关系的函数表达式 (1)抛物线与坐标轴的交点问题,三角形面积计算
(2)抛物线图象的平移性质
年份 题号 题型 分值 抛物线变化情况 设问形式 解题关键点
2023 24 解 答 题 10 关于中心对称 (1)求与坐标轴交点坐标 (2)求抛物线表达式 (3)求不是菱形的平行四边形的面积 (1)抛物线与坐标轴的交点问题
(2)抛物线图象关于中心对称性质
(3)平行四边形的性质:平行四边形的对角线互相平分
典例精讲
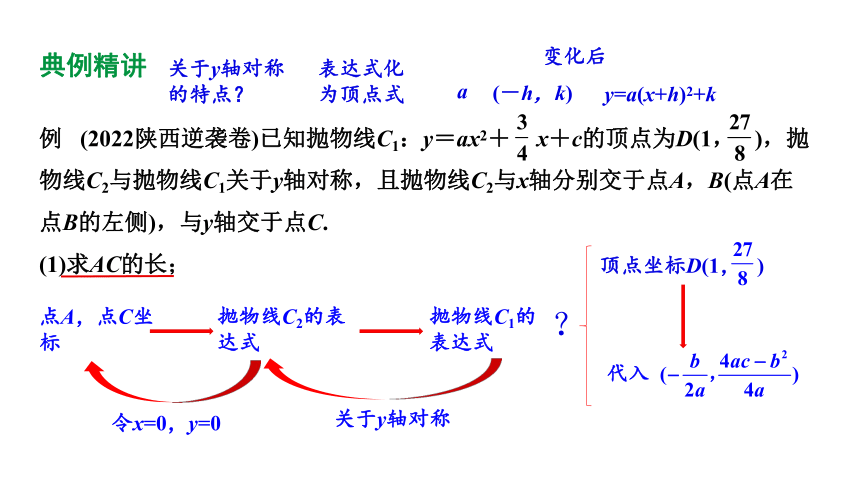
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求AC的长;
点A,点C坐标
?
顶点坐标D(1, )
代入
关于y轴对称
令x=0,y=0
抛物线C2的表达式
抛物线C1的表达式
关于y轴对称的特点?
表达式化为顶点式
变化后
a
(-h,k)
y=a(x+h)2+k
解:(1)∵抛物线C1:y=ax2+ x+c的顶点为D(1, ),
∴抛物线的对称轴为直线x=1,
∴
∴抛物线C1的表达式为y=- x2+ x+3,
∵抛物线C2与抛物线C1关于y轴对称,
∴抛物线C2的表达式为y=- x2- x+3.
∵抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C,
令y=0,则- x2- x+3=0,
解得x=-4或x=2,
∵点A在点B的左侧,
∴A(-4,0),B(2,0).
令x=0,则y=3,
∴C(0,3),
∴AC= ;
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(2)点P是位于AC下方的抛物线C2上一点,过点P的直线l∥AC,是否存在点P,使得直线l被抛物线C2截得的线段长为AC长的3倍?若存在,求出点P的坐标;若不存在,请说明理由.
求线段长需要先求出被截得的两端点,点P为其中一点
被截线段长为15
联立
抛物线表达式
直线l表达式
√
?
直线l∥AC
求出直线AC表达式
系数一样
点击跳转
几何画板
答题步骤
求AC表达式
求直线l表达式
设点P坐标
将P坐标代入l表达式
联立两表达式
利用所截线段长求点坐标
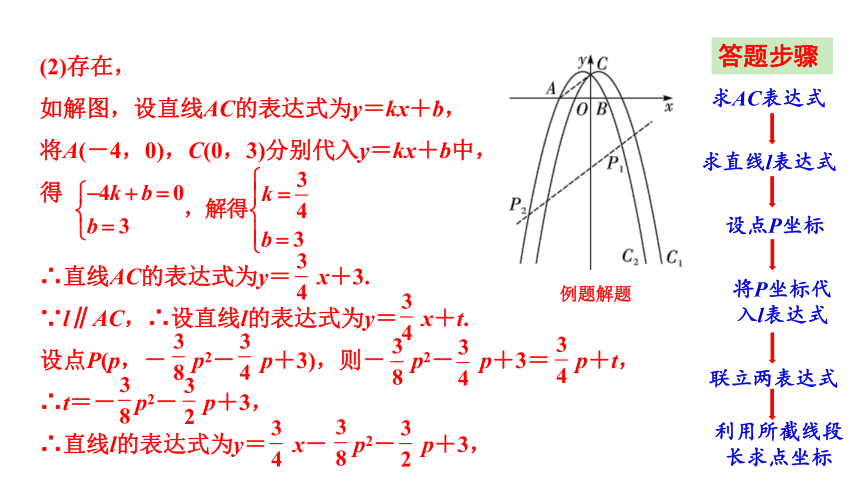
(2)存在,
如解图,设直线AC的表达式为y=kx+b,
将A(-4,0),C(0,3)分别代入y=kx+b中,
得
∴直线AC的表达式为y= x+3.
∵l∥AC,∴设直线l的表达式为y= x+t.
设点P(p,- p2- p+3),则- p2- p+3= p+t,
∴t=- p2- p+3,
∴直线l的表达式为y= x- p2- p+3,
例题解题
联立
∴直线l与抛物线的两个交点为(p,- p2- p+3)和(-p-4,- p2- p).
∵直线l被抛物线C2截得的线段长为AC长的3倍,∴
解得p=4或p=-8,
当p=4时,y=- p2- p+3=-6,
当p=-8时,y=- p2- p+3=-15,
综上所述,满足条件的点P的坐标为(4,-6)或(-8,-15).
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(3)抛物线C3是抛物线C1关于原点O对称的抛物线,求抛物线C3的表达式.
将抛物线C1化为顶点式
求出抛物线C3的表达式
关于原点O对称的特点?
表达式化为顶点式
变化后
-a
(-h,-k)
y=-a(x+h)2-k
(3)抛物线C1的表达式为y=- x2+ x+3=
∵抛物线C3是抛物线C1关于原点对称的抛物线
∴抛物线C3表达式为 .
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(4)在(3)中已知抛物线C3,且抛物线上有一点Q,使得S△ABC=S△ABQ,求点Q的坐标.
抛物线C2
抛物线C1
抛物线C3
关于y轴对称
关于原点O对称
关于x轴对称
点Q与点C关于x轴对称
点Q在抛物线C3上
抛物线C3上与点Q纵坐标相同的另外一点
答题步骤
判断C3与C2关于x轴对称
求点Q1坐标
求点Q2坐标
(4)∵抛物线C2与抛物线C1关于y轴对称,抛物线C3与抛物线C1关于原点O对称
∴抛物线C2与抛物线C3关于x轴对称
∵点C坐标为(0,3)
∴点Q坐标为(0,-3)
将y=-3代入抛物线 中,
解得x1=0,x2=-2
∴使得S△ABC=S△ABQ,点Q坐标为(0,-3),(-2,-3).
方法总结
抛物线的翻折、中心对称
表达式 变式形式 变化后的a值 变化后的顶点坐标 变化后的表达式
y=a(x-h)2+k(a≠0) 关于x轴对称 -a (h,-k) y=-a(x-h)2-k
关于y轴对称 a (-h,k) y=a(x+h)2+k
关于原点O 中心对称 -a (-h,-k) y=-a(x+h)2-k
绕顶点旋转180° -a (h,k) y=-a(x-h)2+k
方法总结
线段、面积问题
线段问题
1.与x轴垂直的线段的长:纵坐标相减(上减下)
2.与y轴垂直的线段的长:横坐标相减(右减左)
3.斜线段时,可过线段端点分别作x轴,y轴垂线构造直角三角形,利用勾股定理、特殊三角函数值或相似进行求解.
面积问题
方法 直接公式法 分割法 补全法
图示 S△ABC= AB h S△ABC= AB h S△ABC= ah
S△ABC=S四边形BDEC-S△ADB-S△AEC
S△ABC= |xB-xA| yC S△ABC= |yA-yB| |xc-xB| S△ABC= |xc-xB| |yA-yD| S△ABC= (|yE-yC|+|yD-yB|) |xE-xD|- |xA-xD| |yD-yB|- |xE-xA| |yE-yC|
课堂练兵
练习 (2022陕西原创卷)在平面直角坐标系中,抛物线L:y=ax2+bx+c经过点A(0,-3),顶点B在x轴上,且对称轴为直线x=2.
(1)求抛物线L的表达式;
c=-3
可得
求得a,b,c
练习题图
解:(1)∵抛物线的对称轴为直线x=2,且顶点B在x轴上,
∴B(2,0),∴可以设抛物线的表达式为y=a(x-2)2,
把A(0,-3)代入y=a(x-2)2,解得a=- .
∴抛物线的表达式为y=- (x-2)2=- x2+3x-3;
练习 (2022陕西原创卷)在平面直角坐标系中,抛物线L:y=ax2+bx+c经过点A(0,-3),顶点B在x轴上,且对称轴为直线x=2.
(2)将该抛物线平移,平移后的抛物线L′的顶点为B′,且与x轴交于C,D两点(点C在点D的左侧),若以A、B、B′、C为顶点的四边形是面积为6的平行四边形,求抛物线L′的表达式.
AB为边,AB∥B′C,AB=B′C
画出草图
情况①:
情况②:
平行四边形ABB′C分割为2个全等三角形,S△ABC=3,找满足S△BB′C=3的B′点
通过对比顶点B和顶点B′确定平移路径
求抛物线L′的表达式
点击跳转
几何画板
(2)当点C在点B的左侧时,
∵四边形ABB′C是平行四边形,∴AB=B′C,AB∥CB′,
∴点B′的纵坐标与点A的纵坐标绝对值相等,
∵A(0,-3),∴点B′的纵坐标为3,
∵平行四边形ABB′C的面积为6,
∴S△BCB′= ×BC×3=3,∴BC=2,
∵B(2,0),∴C(0,0),B′(2,3),
∴抛物线L向上平移3个单位得到抛物线L′,
此时抛物线L′的表达式为y=- x2+3x,
同理可得,当点C在点B的右侧时,C(4,0),B′(6,3),
抛物线L向右平移4个单位,再向上平移3个单位得到抛物线L′,
此时抛物线L′的表达式为y=- x2+9x-24.
∴抛物线L′的表达式为y=- x2+3x或y=- x2+9x-24.
课后小练
练习1 (2022陕西题组小卷)在平面直角坐标系中,抛物线y=ax2+bx+4(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,OA=OC=2OB.
练习题图
(1)求该抛物线的表达式;
解:(1)令x=0,则y=4,∴点C的坐标为(0,4),
∵OA=OC=2OB,∴OA=4,OB=2,
∵点A在点B的左侧,
∴点A的坐标为(-4,0),点B的坐标为(2,0),将点A,B的坐标代入y=ax2+bx+4,可得
∴抛物线的表达式为y=- x2-x+4;
练习1 (2022陕西题组小卷)在平面直角坐标系中,抛物线y=ax2+bx+4(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,OA=OC=2OB.
(2)在抛物线上是否存在点M,使A、C两点到直线MB的距离相等?若存在,求出满足条件的点M的坐标;若不存在,请说明理由.
(2)存在;理由如下:
∵OA=OC,∴线段AC的垂直平分线交x轴于点O,
∴要使点A,C到直线MB的距离相等,分两种情况讨论:
①当直线BM与直线AC平行时,
设直线AC的表达式为y=kx+m,
将点A,C 的坐标代入可得
∴直线AC的表达式为y=x+4,
如解图,设直线M1B的表达式为y=x+n,
∵直线M1B经过点B,即0=2+n,∴n=-2,
∴直线M1B的表达式为y=x-2,
联立抛物线与直线M1B的表达式,
∴点M1的坐标为(-6,-8);
练习题解图
②如解图,设AC的中点为点D,连接BD交抛物线于点M2,过点A作AE⊥BM2于点E,CF⊥BM2于点F.
易得△ADE≌△CDF,∴AE=CF,
∵A(-4,0),C(0,4),∴D(-2,2),
设直线BD的表达式为y=px+q,
将B、D的坐标代入可得
∴直线BD的表达式为y=- x+1,
∴点M2的坐标为(-3, ),
综上所述,点M的坐标为(-6,-8)或(-3, ).
练习题解图
练习2 (2022陕西原创卷)在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B两点,且经过点(2,3),抛物线的对称轴与x轴交于点G.
练习题图
(1)求抛物线的对称轴;
解:(1)把(-1,0),(2,3)代入抛物线中得,
∴抛物线的表达式为y=-x2+2x+3,
∴ ,
∴抛物线的对称轴为直线x=1;
练习2 (2022陕西原创卷)在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B两点,且经过点(2,3),抛物线的对称轴与x轴交于点G.
(2)点D、E在对称轴上(D在E的上方),点F在第一象限,是否存在使得四边形AEBD(AB为对角线)与四边形ABFD(AB为边)都是菱形的情形?若存在,请分别求出此时四边形AEBD与四边形ABFD的面积,若不存在,请说明理由.
(2)存在,令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,∴ B(3,0),∴AB=4,
如解图,当四边形ABFD为菱形时,AD=AB=4,
设D(1,m),在Rt△ADG中,
AD2=AG2+DG2=22+m2=4+m2=16,
解得m1=2 ,m2=-2 (舍去),∴D(1,2 ),
练习题解图
∴S菱形ABFD=AB·DG=4×2 =8 .
当四边形AEBD为菱形时,D、E两点关于x轴对称,
∴E(1,-2 ),即DE=4 ,
∴S菱形AEBD= AB·DE= ×4×4 =8 .
练习题解图
陕西 数学
抛物线与几何综合题
2024中考备考重难专题课件
线段、面积问题
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
抛物线与几何综合题
线段、面积问题
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 抛物线变化情况 设问形式 解题关键点
2018 24 解 答 题 10 平移 (1)求抛物线与坐标轴交点坐标及交点为顶点的三角形面积 (2)求满足面积等量关系的函数表达式 (1)抛物线与坐标轴的交点问题,三角形面积计算
(2)抛物线图象的平移性质
年份 题号 题型 分值 抛物线变化情况 设问形式 解题关键点
2023 24 解 答 题 10 关于中心对称 (1)求与坐标轴交点坐标 (2)求抛物线表达式 (3)求不是菱形的平行四边形的面积 (1)抛物线与坐标轴的交点问题
(2)抛物线图象关于中心对称性质
(3)平行四边形的性质:平行四边形的对角线互相平分
典例精讲
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求AC的长;
点A,点C坐标
?
顶点坐标D(1, )
代入
关于y轴对称
令x=0,y=0
抛物线C2的表达式
抛物线C1的表达式
关于y轴对称的特点?
表达式化为顶点式
变化后
a
(-h,k)
y=a(x+h)2+k
解:(1)∵抛物线C1:y=ax2+ x+c的顶点为D(1, ),
∴抛物线的对称轴为直线x=1,
∴
∴抛物线C1的表达式为y=- x2+ x+3,
∵抛物线C2与抛物线C1关于y轴对称,
∴抛物线C2的表达式为y=- x2- x+3.
∵抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C,
令y=0,则- x2- x+3=0,
解得x=-4或x=2,
∵点A在点B的左侧,
∴A(-4,0),B(2,0).
令x=0,则y=3,
∴C(0,3),
∴AC= ;
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(2)点P是位于AC下方的抛物线C2上一点,过点P的直线l∥AC,是否存在点P,使得直线l被抛物线C2截得的线段长为AC长的3倍?若存在,求出点P的坐标;若不存在,请说明理由.
求线段长需要先求出被截得的两端点,点P为其中一点
被截线段长为15
联立
抛物线表达式
直线l表达式
√
?
直线l∥AC
求出直线AC表达式
系数一样
点击跳转
几何画板
答题步骤
求AC表达式
求直线l表达式
设点P坐标
将P坐标代入l表达式
联立两表达式
利用所截线段长求点坐标
(2)存在,
如解图,设直线AC的表达式为y=kx+b,
将A(-4,0),C(0,3)分别代入y=kx+b中,
得
∴直线AC的表达式为y= x+3.
∵l∥AC,∴设直线l的表达式为y= x+t.
设点P(p,- p2- p+3),则- p2- p+3= p+t,
∴t=- p2- p+3,
∴直线l的表达式为y= x- p2- p+3,
例题解题
联立
∴直线l与抛物线的两个交点为(p,- p2- p+3)和(-p-4,- p2- p).
∵直线l被抛物线C2截得的线段长为AC长的3倍,∴
解得p=4或p=-8,
当p=4时,y=- p2- p+3=-6,
当p=-8时,y=- p2- p+3=-15,
综上所述,满足条件的点P的坐标为(4,-6)或(-8,-15).
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(3)抛物线C3是抛物线C1关于原点O对称的抛物线,求抛物线C3的表达式.
将抛物线C1化为顶点式
求出抛物线C3的表达式
关于原点O对称的特点?
表达式化为顶点式
变化后
-a
(-h,-k)
y=-a(x+h)2-k
(3)抛物线C1的表达式为y=- x2+ x+3=
∵抛物线C3是抛物线C1关于原点对称的抛物线
∴抛物线C3表达式为 .
例 (2022陕西逆袭卷)已知抛物线C1:y=ax2+ x+c的顶点为D(1, ),抛物线C2与抛物线C1关于y轴对称,且抛物线C2与x轴分别交于点A,B(点A在点B的左侧),与y轴交于点C.
(4)在(3)中已知抛物线C3,且抛物线上有一点Q,使得S△ABC=S△ABQ,求点Q的坐标.
抛物线C2
抛物线C1
抛物线C3
关于y轴对称
关于原点O对称
关于x轴对称
点Q与点C关于x轴对称
点Q在抛物线C3上
抛物线C3上与点Q纵坐标相同的另外一点
答题步骤
判断C3与C2关于x轴对称
求点Q1坐标
求点Q2坐标
(4)∵抛物线C2与抛物线C1关于y轴对称,抛物线C3与抛物线C1关于原点O对称
∴抛物线C2与抛物线C3关于x轴对称
∵点C坐标为(0,3)
∴点Q坐标为(0,-3)
将y=-3代入抛物线 中,
解得x1=0,x2=-2
∴使得S△ABC=S△ABQ,点Q坐标为(0,-3),(-2,-3).
方法总结
抛物线的翻折、中心对称
表达式 变式形式 变化后的a值 变化后的顶点坐标 变化后的表达式
y=a(x-h)2+k(a≠0) 关于x轴对称 -a (h,-k) y=-a(x-h)2-k
关于y轴对称 a (-h,k) y=a(x+h)2+k
关于原点O 中心对称 -a (-h,-k) y=-a(x+h)2-k
绕顶点旋转180° -a (h,k) y=-a(x-h)2+k
方法总结
线段、面积问题
线段问题
1.与x轴垂直的线段的长:纵坐标相减(上减下)
2.与y轴垂直的线段的长:横坐标相减(右减左)
3.斜线段时,可过线段端点分别作x轴,y轴垂线构造直角三角形,利用勾股定理、特殊三角函数值或相似进行求解.
面积问题
方法 直接公式法 分割法 补全法
图示 S△ABC= AB h S△ABC= AB h S△ABC= ah
S△ABC=S四边形BDEC-S△ADB-S△AEC
S△ABC= |xB-xA| yC S△ABC= |yA-yB| |xc-xB| S△ABC= |xc-xB| |yA-yD| S△ABC= (|yE-yC|+|yD-yB|) |xE-xD|- |xA-xD| |yD-yB|- |xE-xA| |yE-yC|
课堂练兵
练习 (2022陕西原创卷)在平面直角坐标系中,抛物线L:y=ax2+bx+c经过点A(0,-3),顶点B在x轴上,且对称轴为直线x=2.
(1)求抛物线L的表达式;
c=-3
可得
求得a,b,c
练习题图
解:(1)∵抛物线的对称轴为直线x=2,且顶点B在x轴上,
∴B(2,0),∴可以设抛物线的表达式为y=a(x-2)2,
把A(0,-3)代入y=a(x-2)2,解得a=- .
∴抛物线的表达式为y=- (x-2)2=- x2+3x-3;
练习 (2022陕西原创卷)在平面直角坐标系中,抛物线L:y=ax2+bx+c经过点A(0,-3),顶点B在x轴上,且对称轴为直线x=2.
(2)将该抛物线平移,平移后的抛物线L′的顶点为B′,且与x轴交于C,D两点(点C在点D的左侧),若以A、B、B′、C为顶点的四边形是面积为6的平行四边形,求抛物线L′的表达式.
AB为边,AB∥B′C,AB=B′C
画出草图
情况①:
情况②:
平行四边形ABB′C分割为2个全等三角形,S△ABC=3,找满足S△BB′C=3的B′点
通过对比顶点B和顶点B′确定平移路径
求抛物线L′的表达式
点击跳转
几何画板
(2)当点C在点B的左侧时,
∵四边形ABB′C是平行四边形,∴AB=B′C,AB∥CB′,
∴点B′的纵坐标与点A的纵坐标绝对值相等,
∵A(0,-3),∴点B′的纵坐标为3,
∵平行四边形ABB′C的面积为6,
∴S△BCB′= ×BC×3=3,∴BC=2,
∵B(2,0),∴C(0,0),B′(2,3),
∴抛物线L向上平移3个单位得到抛物线L′,
此时抛物线L′的表达式为y=- x2+3x,
同理可得,当点C在点B的右侧时,C(4,0),B′(6,3),
抛物线L向右平移4个单位,再向上平移3个单位得到抛物线L′,
此时抛物线L′的表达式为y=- x2+9x-24.
∴抛物线L′的表达式为y=- x2+3x或y=- x2+9x-24.
课后小练
练习1 (2022陕西题组小卷)在平面直角坐标系中,抛物线y=ax2+bx+4(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,OA=OC=2OB.
练习题图
(1)求该抛物线的表达式;
解:(1)令x=0,则y=4,∴点C的坐标为(0,4),
∵OA=OC=2OB,∴OA=4,OB=2,
∵点A在点B的左侧,
∴点A的坐标为(-4,0),点B的坐标为(2,0),将点A,B的坐标代入y=ax2+bx+4,可得
∴抛物线的表达式为y=- x2-x+4;
练习1 (2022陕西题组小卷)在平面直角坐标系中,抛物线y=ax2+bx+4(a≠0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,OA=OC=2OB.
(2)在抛物线上是否存在点M,使A、C两点到直线MB的距离相等?若存在,求出满足条件的点M的坐标;若不存在,请说明理由.
(2)存在;理由如下:
∵OA=OC,∴线段AC的垂直平分线交x轴于点O,
∴要使点A,C到直线MB的距离相等,分两种情况讨论:
①当直线BM与直线AC平行时,
设直线AC的表达式为y=kx+m,
将点A,C 的坐标代入可得
∴直线AC的表达式为y=x+4,
如解图,设直线M1B的表达式为y=x+n,
∵直线M1B经过点B,即0=2+n,∴n=-2,
∴直线M1B的表达式为y=x-2,
联立抛物线与直线M1B的表达式,
∴点M1的坐标为(-6,-8);
练习题解图
②如解图,设AC的中点为点D,连接BD交抛物线于点M2,过点A作AE⊥BM2于点E,CF⊥BM2于点F.
易得△ADE≌△CDF,∴AE=CF,
∵A(-4,0),C(0,4),∴D(-2,2),
设直线BD的表达式为y=px+q,
将B、D的坐标代入可得
∴直线BD的表达式为y=- x+1,
∴点M2的坐标为(-3, ),
综上所述,点M的坐标为(-6,-8)或(-3, ).
练习题解图
练习2 (2022陕西原创卷)在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B两点,且经过点(2,3),抛物线的对称轴与x轴交于点G.
练习题图
(1)求抛物线的对称轴;
解:(1)把(-1,0),(2,3)代入抛物线中得,
∴抛物线的表达式为y=-x2+2x+3,
∴ ,
∴抛物线的对称轴为直线x=1;
练习2 (2022陕西原创卷)在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B两点,且经过点(2,3),抛物线的对称轴与x轴交于点G.
(2)点D、E在对称轴上(D在E的上方),点F在第一象限,是否存在使得四边形AEBD(AB为对角线)与四边形ABFD(AB为边)都是菱形的情形?若存在,请分别求出此时四边形AEBD与四边形ABFD的面积,若不存在,请说明理由.
(2)存在,令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,∴ B(3,0),∴AB=4,
如解图,当四边形ABFD为菱形时,AD=AB=4,
设D(1,m),在Rt△ADG中,
AD2=AG2+DG2=22+m2=4+m2=16,
解得m1=2 ,m2=-2 (舍去),∴D(1,2 ),
练习题解图
∴S菱形ABFD=AB·DG=4×2 =8 .
当四边形AEBD为菱形时,D、E两点关于x轴对称,
∴E(1,-2 ),即DE=4 ,
∴S菱形AEBD= AB·DE= ×4×4 =8 .
练习题解图
同课章节目录
