2024陕西数学中考备考重难专题:圆的综合题课件 22张PPT
文档属性
| 名称 | 2024陕西数学中考备考重难专题:圆的综合题课件 22张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 14:27:02 | ||
图片预览




文档简介
(共22张PPT)
陕西 数学
圆的综合题
2024中考备考重难专题课件
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
圆的综合题
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
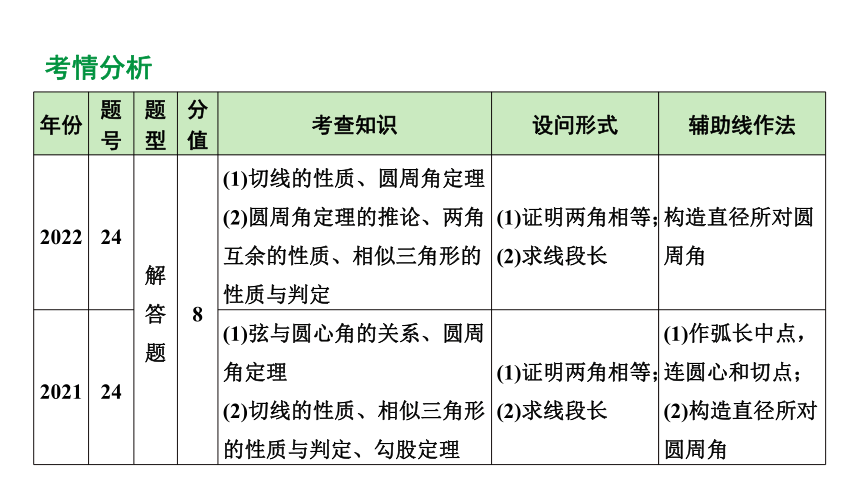
年份 题号 题型 分值 考查知识 设问形式 辅助线作法
2022 24 解答题 8 (1)切线的性质、圆周角定理 (2)圆周角定理的推论、两角互余的性质、相似三角形的性质与判定 (1)证明两角相等; (2)求线段长 构造直径所对圆周角
2021 24 (1)弦与圆心角的关系、圆周角定理 (2)切线的性质、相似三角形的性质与判定、勾股定理 (1)证明两角相等;(2)求线段长 (1)作弧长中点,连圆心和切点;(2)构造直径所对圆周角
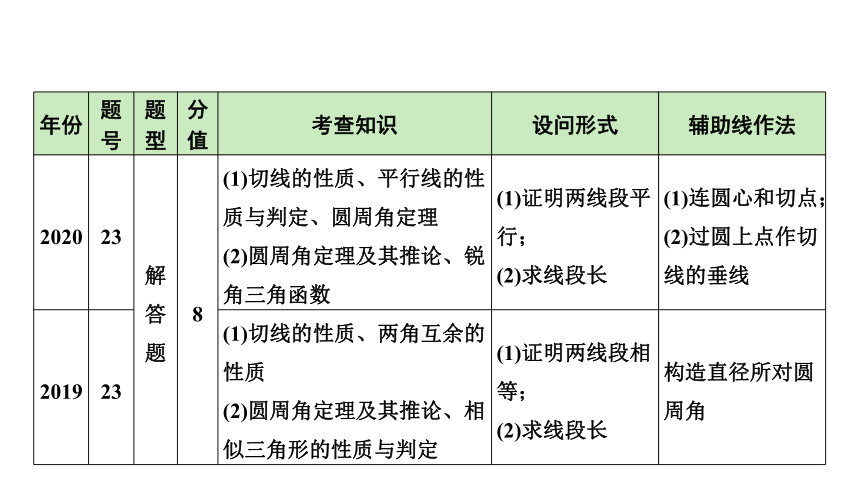
年份 题号 题型 分值 考查知识 设问形式 辅助线作法
2020 23 解答题 8 (1)切线的性质、平行线的性质与判定、圆周角定理 (2)圆周角定理及其推论、锐角三角函数 (1)证明两线段平行; (2)求线段长 (1)连圆心和切点;(2)过圆上点作切线的垂线
2019 23 (1)切线的性质、两角互余的性质 (2)圆周角定理及其推论、相似三角形的性质与判定 (1)证明两线段相等; (2)求线段长 构造直径所对圆周角
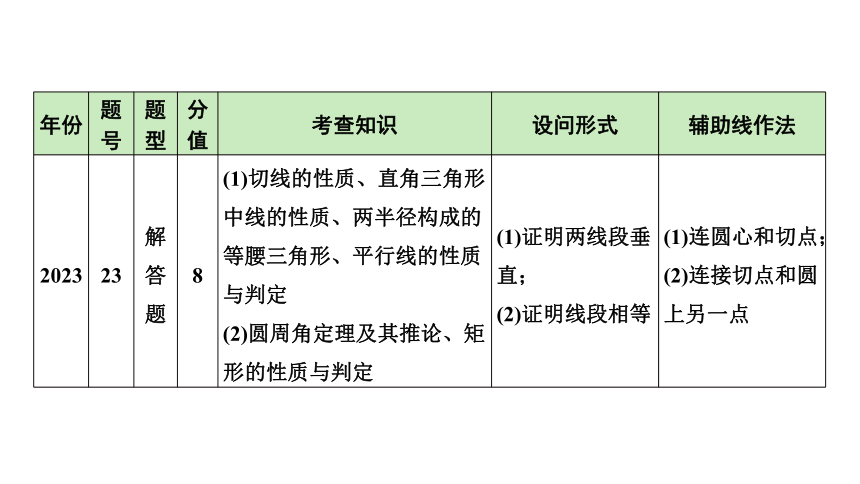
年份 题号 题型 分值 考查知识 设问形式 辅助线作法
2023 23 解答题 8 (1)切线的性质、直角三角形中线的性质、两半径构成的等腰三角形、平行线的性质与判定 (2)圆周角定理及其推论、矩形的性质与判定 (1)证明两线段垂直; (2)证明线段相等 (1)连圆心和切点;(2)连接切点和圆上另一点
典例精讲
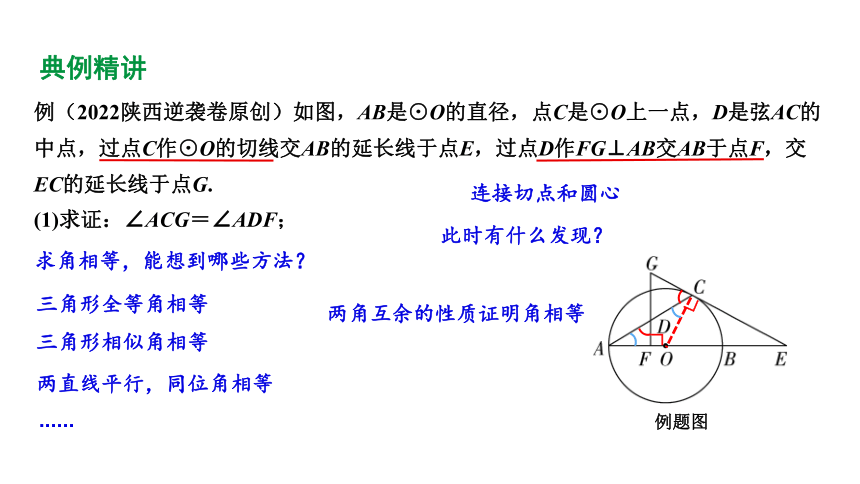
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
(1)求证:∠ACG=∠ADF;
∟
例题图
求角相等,能想到哪些方法?
......
三角形全等角相等
三角形相似角相等
两直线平行,同位角相等
∟
连接切点和圆心
此时有什么发现?
两角互余的性质证明角相等
(1)证明:如图,连接OC,
∵CE是⊙O的切线,
∴∠OCG=90°,
∴∠OCA+∠ACG=90°.
∵FG⊥AB,
∴∠AFD=90°,
∴∠DAF+∠ADF=90°.
∵OA=OC,
∴∠OCA=∠DAF,
∴∠ACG=∠ADF.
∟
答题步骤
作辅助线
证∠OCA+∠ACG=90°
证∠DAF+∠ADF=90°
证∠OCA=∠DAF
则∠ACG=∠ADF
例题图
(2)若⊙O的半径为5,AC=8,求AF的长.
例题图
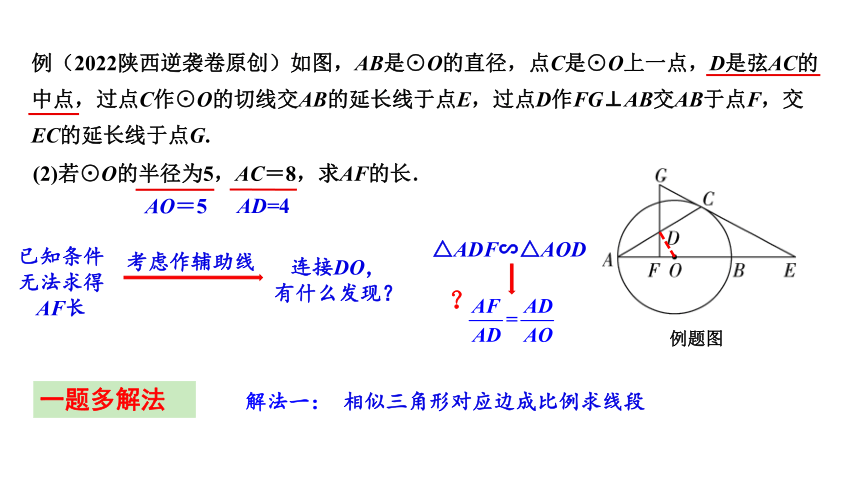
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
AD=4
已知条件无法求得AF长
连接DO,有什么发现?
△ADF∽△AOD
?
相似三角形对应边成比例求线段
一题多解法
解法一:
AO=5
考虑作辅助线
(2)若⊙O的半径为5,AC=8,求AF的长.
例题图
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
相似三角形对应边成比例求线段
一题多解法
解法二:
连接BC有什么发现?
△ADF∽△ABC
AB=10
AD=4
?
AB、AC在哪个三角形中?
△ABC
(2)若⊙O的半径为5,AC=8,求AF的长.
例题图
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
AO=5
AD=4
∟
OD=3
观察△ADO,
有什么发现?
AO·DF= AD·OD
求得DF长
在Rt△DFO中求得OF长
AF=AO-OF
三角形面积计算公式求线段长
一题多解法
解法三:
(2)解:如图,连接OD,
∵D是弦AC的中点,AC=8,
∴∠ADO=90°=∠AFD,AD=CD=4.
∵∠A=∠A,
∴△ADF∽△AOD,
∴ = ,
∴AF= .
∵⊙O的半径为5,
∴AF= = .
答题步骤
作辅助线
求出AD长
证△ADF∽△AOD
写出比例式计算AF
例题图
解法一
方法总结
圆的综合题
切线的性质、圆周角定理及其推论、相似三角形的性质与判定、锐角三角函数、勾股定理
相似A字型,特点为有共用的一组角,且有另外一组角相等,形似字母“A”
过圆心连半径,通常还要再转化构造直径去解题(题中没有给出直径的情况)
知识点:
模型:
辅助线作法:
1.证明角间数量关系
切线的性质,圆周角定理的推论,两半径构成的等腰三角形,角间等量转换,两角互余的性质
2.求线段长
通常有3种方法:
①锐角三角函数,此时线段要在直角三角形中或者能够构造直角三角形,用锐角三角函数需要已知一条边和一个角;
②勾股定理,此时线段要在直角三角形中或者能够构造直角三角形,用勾股定理需要已知两边;
③三角形相似、全等,用相似需要证明两组角相等,有等边则证明全等
圆的综合题
解题方法:
课堂练兵
练习 (2023四川试题研究)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,过点D作⊙O的切线交AC于点F.
(1)如图①,求证:DF⊥AC;
∟
练习题图
∠ABC=∠ACB
知切点,连半径,连接OD
考虑通过证明DO∥AC,证得DF⊥AC
DO∥AC
两直线平行
同旁内角互补
OB=OD
∠ABC=∠ODB
?
(1)证明:如图,连接OD,
∵AB=AC,OB=OD,
∴∠OBD=∠ODB=∠C
∴OD∥AC,
∵DF是⊙O的切线,
∴OD⊥DF,
∴DF⊥AC;
∟
答题步骤
连半径
同位角证OD∥AC
证OD⊥DF
证得DF⊥AC
练习题图
(2)如图②,连接AD,求证:CD2=CF·AC.
练习 (四川2023试题研究)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,过点D作⊙O的切线交AC于点F.
练习题图
看到这个,怎么求线段关系?
线段分别在哪个三角形中?
△DCF、△ACD
是否相似?
∟
∟
△DCF∽△ACD
两三角形相似
对应边成比例
(2)解∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°.
由(1)知DF⊥AC,
∴∠CFD=90°.
∵∠DCF=∠ACD,∠C=∠C
∴△DCF∽△ACD,
∴ = ,
∴CD2=CF·AC.
答题步骤
证∠ADC=∠CFD=90°
证△DCF∽△ACD
写相似比
证得CD2=CF·AC
练习题图
课后小练
练习1 (2022西安模拟卷)如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E.
(1)求证:∠CDE=∠CAD;
(1)证明:∵OA=OD,∴∠OAD=∠ODA.
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ODA+∠ODB=90°.
∵AE是⊙O的切线,
∴∠OAC=90°,即∠OAD+∠CAD=90°.
∴∠ODB=∠CAD
∵∠ODB=∠CDE,∴∠CDE=∠CAD;
练习1题图
(2)若CD=4,tanB= ,求⊙O的半径.
(2)∵∠CAD+∠BAD=90°,∠BAD+∠B=90°,∴∠CAD=∠B.
∵∠CDE=∠CAD,∠C=∠C,∴△CDE∽△CAD,
∴ = .
∵tan ∠CAD= =tan B= ,∴CA= CD=4 .
在Rt△AOC中,OA2+AC2=OC2,
即OA2+(4 )2=(OA+4)2,解得OA=2,
∴⊙O的半径为2.
练习1题图
练习1 (2022西安模拟卷)如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E.
练习2 如图,在Rt△ABC中,∠ABC=90°,点D是AC上一点,以AD为直径的⊙O与BC相切于点E,与AB交于点F,连接OF,EF,DE.
(1)求证:ED=EF;
(1)证明:如图,连接OE,
∵BC为⊙O的切线,∴OE⊥BC,
∵∠ABC=90°,∴OE∥AB,
∴∠FAO=∠EOD,∠AFO=∠FOE,
∵OA=OF,∴∠FAO=∠AFO,
∴∠EOD =∠FOE,
∴ED=EF;
∟
练习2题图
(2)若AB=6,⊙O的半径为4,求BC的长.
(2)解:由(1)可得OE∥AB,
∴△ABC∽△OEC,
∴ = ,
即 = ,解得DC=4,
∴AC=AD+DC=12,
∴在Rt△ABC中,BC= = =6 .
∟
练习2题图
练习2 如图,在Rt△ABC中,∠ABC=90°,点D是AC上一点,以AD为直径的⊙O与BC相切于点E,与AB交于点F,连接OF,EF,DE.
陕西 数学
圆的综合题
2024中考备考重难专题课件
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
圆的综合题
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 考查知识 设问形式 辅助线作法
2022 24 解答题 8 (1)切线的性质、圆周角定理 (2)圆周角定理的推论、两角互余的性质、相似三角形的性质与判定 (1)证明两角相等; (2)求线段长 构造直径所对圆周角
2021 24 (1)弦与圆心角的关系、圆周角定理 (2)切线的性质、相似三角形的性质与判定、勾股定理 (1)证明两角相等;(2)求线段长 (1)作弧长中点,连圆心和切点;(2)构造直径所对圆周角
年份 题号 题型 分值 考查知识 设问形式 辅助线作法
2020 23 解答题 8 (1)切线的性质、平行线的性质与判定、圆周角定理 (2)圆周角定理及其推论、锐角三角函数 (1)证明两线段平行; (2)求线段长 (1)连圆心和切点;(2)过圆上点作切线的垂线
2019 23 (1)切线的性质、两角互余的性质 (2)圆周角定理及其推论、相似三角形的性质与判定 (1)证明两线段相等; (2)求线段长 构造直径所对圆周角
年份 题号 题型 分值 考查知识 设问形式 辅助线作法
2023 23 解答题 8 (1)切线的性质、直角三角形中线的性质、两半径构成的等腰三角形、平行线的性质与判定 (2)圆周角定理及其推论、矩形的性质与判定 (1)证明两线段垂直; (2)证明线段相等 (1)连圆心和切点;(2)连接切点和圆上另一点
典例精讲
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
(1)求证:∠ACG=∠ADF;
∟
例题图
求角相等,能想到哪些方法?
......
三角形全等角相等
三角形相似角相等
两直线平行,同位角相等
∟
连接切点和圆心
此时有什么发现?
两角互余的性质证明角相等
(1)证明:如图,连接OC,
∵CE是⊙O的切线,
∴∠OCG=90°,
∴∠OCA+∠ACG=90°.
∵FG⊥AB,
∴∠AFD=90°,
∴∠DAF+∠ADF=90°.
∵OA=OC,
∴∠OCA=∠DAF,
∴∠ACG=∠ADF.
∟
答题步骤
作辅助线
证∠OCA+∠ACG=90°
证∠DAF+∠ADF=90°
证∠OCA=∠DAF
则∠ACG=∠ADF
例题图
(2)若⊙O的半径为5,AC=8,求AF的长.
例题图
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
AD=4
已知条件无法求得AF长
连接DO,有什么发现?
△ADF∽△AOD
?
相似三角形对应边成比例求线段
一题多解法
解法一:
AO=5
考虑作辅助线
(2)若⊙O的半径为5,AC=8,求AF的长.
例题图
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
相似三角形对应边成比例求线段
一题多解法
解法二:
连接BC有什么发现?
△ADF∽△ABC
AB=10
AD=4
?
AB、AC在哪个三角形中?
△ABC
(2)若⊙O的半径为5,AC=8,求AF的长.
例题图
例(2022陕西逆袭卷原创)如图,AB是⊙O的直径,点C是⊙O上一点,D是弦AC的中点,过点C作⊙O的切线交AB的延长线于点E,过点D作FG⊥AB交AB于点F,交EC的延长线于点G.
AO=5
AD=4
∟
OD=3
观察△ADO,
有什么发现?
AO·DF= AD·OD
求得DF长
在Rt△DFO中求得OF长
AF=AO-OF
三角形面积计算公式求线段长
一题多解法
解法三:
(2)解:如图,连接OD,
∵D是弦AC的中点,AC=8,
∴∠ADO=90°=∠AFD,AD=CD=4.
∵∠A=∠A,
∴△ADF∽△AOD,
∴ = ,
∴AF= .
∵⊙O的半径为5,
∴AF= = .
答题步骤
作辅助线
求出AD长
证△ADF∽△AOD
写出比例式计算AF
例题图
解法一
方法总结
圆的综合题
切线的性质、圆周角定理及其推论、相似三角形的性质与判定、锐角三角函数、勾股定理
相似A字型,特点为有共用的一组角,且有另外一组角相等,形似字母“A”
过圆心连半径,通常还要再转化构造直径去解题(题中没有给出直径的情况)
知识点:
模型:
辅助线作法:
1.证明角间数量关系
切线的性质,圆周角定理的推论,两半径构成的等腰三角形,角间等量转换,两角互余的性质
2.求线段长
通常有3种方法:
①锐角三角函数,此时线段要在直角三角形中或者能够构造直角三角形,用锐角三角函数需要已知一条边和一个角;
②勾股定理,此时线段要在直角三角形中或者能够构造直角三角形,用勾股定理需要已知两边;
③三角形相似、全等,用相似需要证明两组角相等,有等边则证明全等
圆的综合题
解题方法:
课堂练兵
练习 (2023四川试题研究)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,过点D作⊙O的切线交AC于点F.
(1)如图①,求证:DF⊥AC;
∟
练习题图
∠ABC=∠ACB
知切点,连半径,连接OD
考虑通过证明DO∥AC,证得DF⊥AC
DO∥AC
两直线平行
同旁内角互补
OB=OD
∠ABC=∠ODB
?
(1)证明:如图,连接OD,
∵AB=AC,OB=OD,
∴∠OBD=∠ODB=∠C
∴OD∥AC,
∵DF是⊙O的切线,
∴OD⊥DF,
∴DF⊥AC;
∟
答题步骤
连半径
同位角证OD∥AC
证OD⊥DF
证得DF⊥AC
练习题图
(2)如图②,连接AD,求证:CD2=CF·AC.
练习 (四川2023试题研究)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,过点D作⊙O的切线交AC于点F.
练习题图
看到这个,怎么求线段关系?
线段分别在哪个三角形中?
△DCF、△ACD
是否相似?
∟
∟
△DCF∽△ACD
两三角形相似
对应边成比例
(2)解∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°.
由(1)知DF⊥AC,
∴∠CFD=90°.
∵∠DCF=∠ACD,∠C=∠C
∴△DCF∽△ACD,
∴ = ,
∴CD2=CF·AC.
答题步骤
证∠ADC=∠CFD=90°
证△DCF∽△ACD
写相似比
证得CD2=CF·AC
练习题图
课后小练
练习1 (2022西安模拟卷)如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E.
(1)求证:∠CDE=∠CAD;
(1)证明:∵OA=OD,∴∠OAD=∠ODA.
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ODA+∠ODB=90°.
∵AE是⊙O的切线,
∴∠OAC=90°,即∠OAD+∠CAD=90°.
∴∠ODB=∠CAD
∵∠ODB=∠CDE,∴∠CDE=∠CAD;
练习1题图
(2)若CD=4,tanB= ,求⊙O的半径.
(2)∵∠CAD+∠BAD=90°,∠BAD+∠B=90°,∴∠CAD=∠B.
∵∠CDE=∠CAD,∠C=∠C,∴△CDE∽△CAD,
∴ = .
∵tan ∠CAD= =tan B= ,∴CA= CD=4 .
在Rt△AOC中,OA2+AC2=OC2,
即OA2+(4 )2=(OA+4)2,解得OA=2,
∴⊙O的半径为2.
练习1题图
练习1 (2022西安模拟卷)如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E.
练习2 如图,在Rt△ABC中,∠ABC=90°,点D是AC上一点,以AD为直径的⊙O与BC相切于点E,与AB交于点F,连接OF,EF,DE.
(1)求证:ED=EF;
(1)证明:如图,连接OE,
∵BC为⊙O的切线,∴OE⊥BC,
∵∠ABC=90°,∴OE∥AB,
∴∠FAO=∠EOD,∠AFO=∠FOE,
∵OA=OF,∴∠FAO=∠AFO,
∴∠EOD =∠FOE,
∴ED=EF;
∟
练习2题图
(2)若AB=6,⊙O的半径为4,求BC的长.
(2)解:由(1)可得OE∥AB,
∴△ABC∽△OEC,
∴ = ,
即 = ,解得DC=4,
∴AC=AD+DC=12,
∴在Rt△ABC中,BC= = =6 .
∟
练习2题图
练习2 如图,在Rt△ABC中,∠ABC=90°,点D是AC上一点,以AD为直径的⊙O与BC相切于点E,与AB交于点F,连接OF,EF,DE.
同课章节目录
