2024陕西数学中考备考重难专题:综合与实践面积问题课件 27张PPT
文档属性
| 名称 | 2024陕西数学中考备考重难专题:综合与实践面积问题课件 27张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 14:29:26 | ||
图片预览







文档简介
(共27张PPT)
陕西 数学
综合与实践
2024中考备考重难专题课件
面积问题
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
综合与实践
面积问题
课后小练
1
典例精讲
2
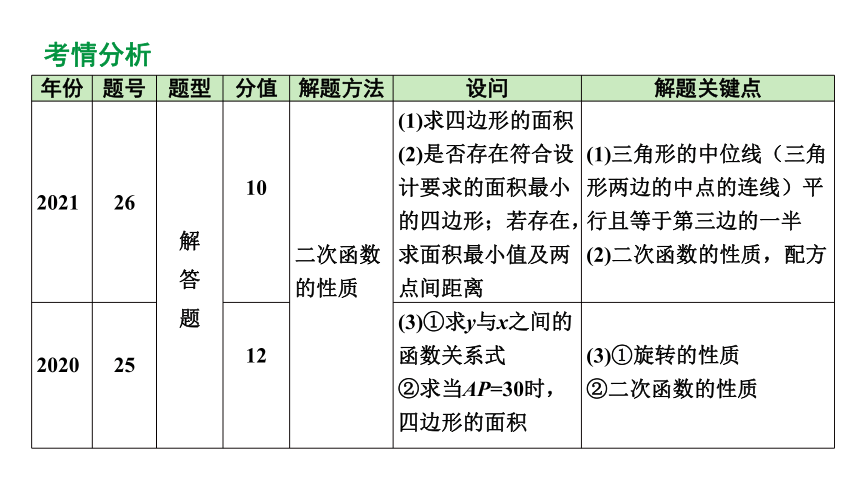
年份 题号 题型 分值 解题方法 设问 解题关键点
2021 26 解 答 题 10 二次函数的性质 (1)求四边形的面积 (2)是否存在符合设计要求的面积最小的四边形;若存在,求面积最小值及两点间距离
(1)三角形的中位线(三角形两边的中点的连线)平行且等于第三边的一半
(2)二次函数的性质,配方
2020 25 12 (3)①求y与x之间的函数关系式 ②求当AP=30时,四边形的面积
(3)①旋转的性质
②二次函数的性质
考情分析
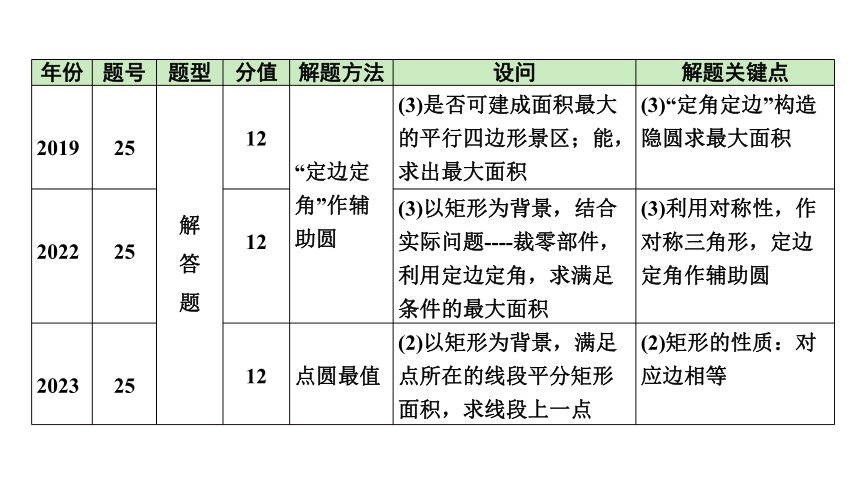
年份 题号 题型 分值 解题方法 设问 解题关键点
2019 25 解 答 题 12 “定边定角”作辅助圆 (3)是否可建成面积最大的平行四边形景区;能,求出最大面积 (3)“定角定边”构造隐圆求最大面积
2022 25 12 (3)以矩形为背景,结合实际问题----裁零部件,利用定边定角,求满足条件的最大面积 (3)利用对称性,作对称三角形,定边定角作辅助圆
2023 25 12 点圆最值 (2)以矩形为背景,满足点所在的线段平分矩形面积,求线段上一点 (2)矩形的性质:对应边相等
典例精讲
例1 (2022陕西逆袭卷)问题提出
(1)如图①,在等腰直角△ABC中,AB=BC,∠ABC=90°,延长AC至点D,使得CD=AC,连接DB,过点A作AE⊥DB交DB的延长线于点E.若AE=2,求△ADE的面积;
例1题图①
点C是AD的中点?
看到中点,能想到哪些跟中点有关的性质?
中位线
过点C作ED垂线
△AEB≌△BFC
F
求得EF长
中位线:平行,且等于第三边的一半,直角三角形斜边上的中线等于斜边的一半,倍长中线,构造全等
解:(1)如解图①,过点C作CF⊥BD于点F,
∵AE⊥BD,∴AE∥CF,
∵CD=AC,∴C是AD的中点,
∴CF是△ADE的中位线,
∴CF= AE=1,EF=DF.
∵∠ABC=90°,
∴∠ABE+∠CBF=90°.
∵AE⊥EF,∴∠EAB+∠ABE=90°,
∴∠EAB=∠CBF.
在△AEB和△BFC中, ,
∴△AEB≌△BFC,∴BF=AE=2,BE=CF=1,
∴DF=EF=BE+BF=3,
∴ED=EF+DF=6,
∴S△ADE= AE·DE=6;
解图①
问题解决
(2)如图②,农民张大爷家有一块菜园,其形状为等腰△ABC,其中AB=AC,菜园周围是空地,为了方便种菜,他在边AB上选取了一点D,在菜地中修筑了一条小路CD.为了方便蔬菜储存和运输,他计划在菜地外的空地上修建一个临时仓库△BDE.他的设计是:将线段CD绕点D逆时针旋转90°得到线段DE,连接BE,当点D在合适的位置时,临时仓库的面积恰好最大(即△BDE的面积最大).若已知AB=50米,BC=80米,请通过计算,判断张大爷的设想是否成立?若成立,
求出临时仓库面积的最大值;若不成立,请说明理由.
例1题图②
根据S= 底×高→作BD边上的高
即S△BDE= ×BD×EN
?
作辅助线构造全等或相似求解
过点C作CM⊥BA延长线于点M
过点E作EN⊥BA延长线于点N
△EDN≌△DCM→EN=DM→DM=DA+AM
N
M
(2)张大爷的设想成立.
如解图②,分别过点C,E作BA的垂线,垂足记为M,N,过点A作AG⊥BC于点G,
∵AB=AC=50米,BC=80米,∴BG=CG=40米,
∴在Rt△ABG中,由勾股定理得AG= =30米.
∵S△ABC= BC·AG= AB·CM,
∴CM= =48米.
∴在Rt△AMC中,由勾股定理得AM= =14米.
∵∠CDE=90°,∴∠CDM+∠NDE=90°.
∵CM⊥DM,EN⊥DN,∴∠CMD=∠DNE=90°,∠MDC+∠MCD=90°,
解图②
∴∠EDN=∠DCM.
∵DE=DC,∴△EDN≌△DCM(AAS),
∴EN=DM,
设BD=x米,则AD=AB-BD=(50-x)米,
∴EN=DM=DA+AM=50-x+14=(64-x)米,
∴S△BDE= BD·EN= x(64-x)=(- (x-32)2+512)平方米.
∵- <0,0<x<50,
∴当x=32时,临时仓库的面积最大,最大值为512平方米.
解图②
例2 (2022陕西预测卷)
问题提出
(1)如图①,在△ABC中,AB=8,AC=6,D为BC边上的中点,连接AD,则AD的取值范围为______;
例2题图
结合图象,能想到什么?
倍长中线
延长AD到E,使得AD=DE,连接BE
△ADC≌△EDB(SAS)
在△ABE中,由三边关系求取值范围
E
解:如解图①,延长AD至点E,使得DE=AD,连接BE,
∵D为BC上的中点,∴BD=DC,
又∵AD=DE,∠ADC=∠EDB,
∴△ADC≌△EDB(SAS),∴AC=BE=6,
在△ABE中,由三边关系得2解图①
问题探究
(2)如图②,在△ABC中,BC=6,∠BAC=45°,求△ABC面积的最大值;
例2题图②
S△ABC= ×BC×AH
“定边定角”作辅助圆
作△ABC的外接圆⊙O,连接OA、OB,过点A作AH⊥BC于点H,过点O作OD⊥BC于点D
O
H
D
定值
AH取最大,
S△ABC面积最大
观察图形什么时候AH取最大?
注意∠BAC=45°
解图②
(2)如解图②,∵BC=6,∠BAC=45°,
∴作△ABC的外接圆⊙O,连接OA、OB,过点A作AH⊥BC于点H,过点O作OD⊥BC于点D,
∴BD= BC=3,∠BOD=∠BAC=45°,
在Rt△BOD中,OB=3 ,OD=BD=3 ,
∴OA=OB=3 ,
∵AH≤OA+OD=3+3 ,
∴当点D、H重合时,取等号,
∴AHmax=3+3 ,∴S△ABC(max)=9+9 ;
问题解决
(3)如图③,某市政中心计划由旧城改造出一块圆形空地⊙O,并设计修建一个户外健身区△ABC,要求点A在劣弧上,已知户外健身区中间有条已修好的小路AD,且AD=200 米(道路宽度忽略不计),根据设计要求小路AD两侧的面积相等,要使户外健身区△ABC的面积尽可能的大,且∠ABC+∠ACB=60°,试问能否建一个满足要求的面积最大的户外健身区△ABC?若能,请求出△ABC面积的最大值,及此时⊙O的直径;若不能,请说明理由.
例2题图③
点D为BC中点
当点D为BC中点,参考(1)中作法,想到怎么作辅助线?
延长AD至点E,使DE=AD
△CDE≌△BDA
→S△ABC=S△AEC
S△AEC中,∠ACE=60°,AE为定值,参考(2)中作法,作△AEC的外接圆,求S△AEC最大值
E
点C在外接圆的直径上,且垂直AE时,S△AEC最大,此时△AEC为等边三角形
(3)能;
如解图③,延长AD至点E,使DE=AD=200 米,连接CE,易证△CDE≌△BDA,
∴∠DCE=∠CBA,S△ABC=S△AEC,
∵∠ABC+∠ACB=60°,∴∠ACE=60°,AE=400 米,
∴作△ACE的外接圆⊙P,连接CP、EP、DP,
则DP⊥AE,∠EPD=∠ECA=60°.
∴在Rt△PDE中,PD=200米,PE=400米,∴CP=EP=400米.
过点C作CH⊥AE于点H,
∵CH≤PC+PD=600米,∴当点D、H重合时,取等号,∴CHmax=600米,
解图③
解图④
∴S△AEC(max)= AE·CH=120000 平方米,
∴S△ABC(max)=120000 平方米.
当△ABC的面积最大时,
△ABC是等腰三角形,此时△AEC为等边三角形,
如解图④,连接AO,CO,在Rt△ADC中,AD=200 米,∠ACD=30°,
∴AC=400 米,∴OA=OC=400 米,
∴⊙O的直径为800 米.
综上所述,满足要求的户外健身区△ABC最大面积为120000 平方米,此时⊙O的直径为800 米.
课后小练
练习1 (2022陕西黑白卷)问题提出
(1)如图①,在四边形ABCD中,AB=AD,∠B与∠D互补,BC=2CD=20,点A到BC的距离为17,求四边形ABCD的面积;
练习1题图
解:(1)如解图①,连接AC,过点A作AH⊥BC于点H,将△ABH绕点A逆时针旋转,使得AB与AD重合,得到△ADG,∴∠B=∠ADG.
∵∠B与∠ADC互补,∴∠ADC+∠ADG=180°,
∴C,D,G三点共线.
∵点A到BC的距离为17,∴AH=17.
∵BC=2CD=20,∴CD=10.
由旋转的性质得△ADG≌△ABH,∴∠G=∠AHB=90°,AG=AH=17,
∴S△ACD= CD·AG= ×10×17=85,
S△ABC= BC·AH= ×20×17=170,
∴S四边形ABCD=S△ABC+S△ACD=170+85=255;
解题①
问题解决
(2)如图②,某公园计划在一块空地上修建两大主题活动区域,其中△ABE为健身活动区域,△CDE为文艺活动区域,已知AB=BC=60 m,∠B=60°,AB∥CD.按照设计要求,现要在BC上找一点E,使得AE=ED,∠AED=60°,请问是否存在满足设计要求的点E,使得文艺活动区域的面积尽可能大?若存在,求出文艺活动区域的面积及此时点B,E之间的距离;若不存在,请说明理由.
练习1题图
(2)存在.如解图②,连接AC,过点D作DF⊥BC交BC的延长线于点F.
∵AB=BC,∠B=60°,∴△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
又∵AE=ED,∠AED=60°,
∴△AED为等边三角形,∴AE=AD,∠EAD=60°.
∵∠BAE=∠BAC-∠EAC=60°-∠EAC,
∠CAD=∠EAD-∠EAC=60°-∠EAC,
∴∠BAE=∠CAD.
在△BAE和△CAD中, ,
∴△BAE≌△CAD(SAS),∴BE=CD=BC-EC=60-EC.
解题②
∵CD∥AB,
∴∠DCF=∠B=60°.
设CE=x,则BE=CD=60-x,
在Rt△DCF中,DF=DC·sin 60°=(60-x)× =30 - x,
∴S△ECD= CE·DF= x(30 - x)=- (x-30)2+225 ,
∵- <0,
∴当EC=30时,S△CDE有最大值,最大值为225 ,此时BE=60-x=30.
答:存在满足设计要求的点E,此时文艺活动区域的面积为225 m2,点B,E之间的距离为30 m.
解题②
练习2 (2022陕西预测卷)
(1)如图①,在平行四边形ABCD中,AB+BC=10,sinA= ,设AB=x,平行四边形ABCD的面积为y,求出y与x之间的函数表达式,并计算当x的值为多少时,y的值最大,且y的最大值为多少?
练习2题图
解:(1)如解图①,过点B作BE⊥AD交AD于点E,
在ABCD中,AB+BC=10,AD=BC,AB=x,则AD=10-x,
在Rt△ABE中,sin A= ,故BE=AB·sin A= x,
∴y=AD·BE=(10-x)× x=- x2+8x,
∵y=- x2+8x=- (x2-10x+25)+20=- (x-5)2+20,
∵- <0,0∴当x=5时,ymax=20;
解图①
(2)如图②,某商业规划用地的平面示意图为△ABC,规划局拟定在△ABC中规划出一片建筑群,其占地平面示意图为四边形AEDF,其中D为BC上一点,过点D分别作DE∥AC,DF∥AB,且点E、F分别在AB、AC上.经过实地测量后得知:∠BAC=60°,BC=600m,且点D为BC的三等分点(BD<CD),现要求建筑群所在的四边形AEDF的面积最大,请你通过论证并计算出建筑群(即四边形AEDF)所占面积最大为多少?
练习2题图
(2)由DE∥AC,DF∥AB可知:△EBD∽△ABC,△FDC∽△ABC,∴△ABC∽△EBD∽△FDC,
又∵点D为BC的三等分点,∴ ,
设S△ABC=x,则S△EBD= x,S△FDC= x,
故S四边形AEDF=S△ABC-S△EBD-S△FDC= x.
故当x最大时,四边形AEDF的面积最大.
如解图②,作△ABC的外接圆O,连接OA、OB、OC,并过点O作OG⊥BC,
过点A作AH⊥BC,
由∠BAC=60°,可知:∠BOC=120°,BG=GC=300 ,故OG=
=300,OB=2OG=600,
解图②
解图②
∵S△ABC= BC·AH=300 ·AH,AH≤OA+OG,
∴S△ABCmax=300 (OA+OG)=300 (600+300)=270000 ,
∴S四边形AEDFmax= ×270000 =120000 (m2),
即四边形AEDF所占面积最大为120000 m2.
陕西 数学
综合与实践
2024中考备考重难专题课件
面积问题
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
综合与实践
面积问题
课后小练
1
典例精讲
2
年份 题号 题型 分值 解题方法 设问 解题关键点
2021 26 解 答 题 10 二次函数的性质 (1)求四边形的面积 (2)是否存在符合设计要求的面积最小的四边形;若存在,求面积最小值及两点间距离
(1)三角形的中位线(三角形两边的中点的连线)平行且等于第三边的一半
(2)二次函数的性质,配方
2020 25 12 (3)①求y与x之间的函数关系式 ②求当AP=30时,四边形的面积
(3)①旋转的性质
②二次函数的性质
考情分析
年份 题号 题型 分值 解题方法 设问 解题关键点
2019 25 解 答 题 12 “定边定角”作辅助圆 (3)是否可建成面积最大的平行四边形景区;能,求出最大面积 (3)“定角定边”构造隐圆求最大面积
2022 25 12 (3)以矩形为背景,结合实际问题----裁零部件,利用定边定角,求满足条件的最大面积 (3)利用对称性,作对称三角形,定边定角作辅助圆
2023 25 12 点圆最值 (2)以矩形为背景,满足点所在的线段平分矩形面积,求线段上一点 (2)矩形的性质:对应边相等
典例精讲
例1 (2022陕西逆袭卷)问题提出
(1)如图①,在等腰直角△ABC中,AB=BC,∠ABC=90°,延长AC至点D,使得CD=AC,连接DB,过点A作AE⊥DB交DB的延长线于点E.若AE=2,求△ADE的面积;
例1题图①
点C是AD的中点?
看到中点,能想到哪些跟中点有关的性质?
中位线
过点C作ED垂线
△AEB≌△BFC
F
求得EF长
中位线:平行,且等于第三边的一半,直角三角形斜边上的中线等于斜边的一半,倍长中线,构造全等
解:(1)如解图①,过点C作CF⊥BD于点F,
∵AE⊥BD,∴AE∥CF,
∵CD=AC,∴C是AD的中点,
∴CF是△ADE的中位线,
∴CF= AE=1,EF=DF.
∵∠ABC=90°,
∴∠ABE+∠CBF=90°.
∵AE⊥EF,∴∠EAB+∠ABE=90°,
∴∠EAB=∠CBF.
在△AEB和△BFC中, ,
∴△AEB≌△BFC,∴BF=AE=2,BE=CF=1,
∴DF=EF=BE+BF=3,
∴ED=EF+DF=6,
∴S△ADE= AE·DE=6;
解图①
问题解决
(2)如图②,农民张大爷家有一块菜园,其形状为等腰△ABC,其中AB=AC,菜园周围是空地,为了方便种菜,他在边AB上选取了一点D,在菜地中修筑了一条小路CD.为了方便蔬菜储存和运输,他计划在菜地外的空地上修建一个临时仓库△BDE.他的设计是:将线段CD绕点D逆时针旋转90°得到线段DE,连接BE,当点D在合适的位置时,临时仓库的面积恰好最大(即△BDE的面积最大).若已知AB=50米,BC=80米,请通过计算,判断张大爷的设想是否成立?若成立,
求出临时仓库面积的最大值;若不成立,请说明理由.
例1题图②
根据S= 底×高→作BD边上的高
即S△BDE= ×BD×EN
?
作辅助线构造全等或相似求解
过点C作CM⊥BA延长线于点M
过点E作EN⊥BA延长线于点N
△EDN≌△DCM→EN=DM→DM=DA+AM
N
M
(2)张大爷的设想成立.
如解图②,分别过点C,E作BA的垂线,垂足记为M,N,过点A作AG⊥BC于点G,
∵AB=AC=50米,BC=80米,∴BG=CG=40米,
∴在Rt△ABG中,由勾股定理得AG= =30米.
∵S△ABC= BC·AG= AB·CM,
∴CM= =48米.
∴在Rt△AMC中,由勾股定理得AM= =14米.
∵∠CDE=90°,∴∠CDM+∠NDE=90°.
∵CM⊥DM,EN⊥DN,∴∠CMD=∠DNE=90°,∠MDC+∠MCD=90°,
解图②
∴∠EDN=∠DCM.
∵DE=DC,∴△EDN≌△DCM(AAS),
∴EN=DM,
设BD=x米,则AD=AB-BD=(50-x)米,
∴EN=DM=DA+AM=50-x+14=(64-x)米,
∴S△BDE= BD·EN= x(64-x)=(- (x-32)2+512)平方米.
∵- <0,0<x<50,
∴当x=32时,临时仓库的面积最大,最大值为512平方米.
解图②
例2 (2022陕西预测卷)
问题提出
(1)如图①,在△ABC中,AB=8,AC=6,D为BC边上的中点,连接AD,则AD的取值范围为______;
例2题图
结合图象,能想到什么?
倍长中线
延长AD到E,使得AD=DE,连接BE
△ADC≌△EDB(SAS)
在△ABE中,由三边关系求取值范围
E
解:如解图①,延长AD至点E,使得DE=AD,连接BE,
∵D为BC上的中点,∴BD=DC,
又∵AD=DE,∠ADC=∠EDB,
∴△ADC≌△EDB(SAS),∴AC=BE=6,
在△ABE中,由三边关系得2
问题探究
(2)如图②,在△ABC中,BC=6,∠BAC=45°,求△ABC面积的最大值;
例2题图②
S△ABC= ×BC×AH
“定边定角”作辅助圆
作△ABC的外接圆⊙O,连接OA、OB,过点A作AH⊥BC于点H,过点O作OD⊥BC于点D
O
H
D
定值
AH取最大,
S△ABC面积最大
观察图形什么时候AH取最大?
注意∠BAC=45°
解图②
(2)如解图②,∵BC=6,∠BAC=45°,
∴作△ABC的外接圆⊙O,连接OA、OB,过点A作AH⊥BC于点H,过点O作OD⊥BC于点D,
∴BD= BC=3,∠BOD=∠BAC=45°,
在Rt△BOD中,OB=3 ,OD=BD=3 ,
∴OA=OB=3 ,
∵AH≤OA+OD=3+3 ,
∴当点D、H重合时,取等号,
∴AHmax=3+3 ,∴S△ABC(max)=9+9 ;
问题解决
(3)如图③,某市政中心计划由旧城改造出一块圆形空地⊙O,并设计修建一个户外健身区△ABC,要求点A在劣弧上,已知户外健身区中间有条已修好的小路AD,且AD=200 米(道路宽度忽略不计),根据设计要求小路AD两侧的面积相等,要使户外健身区△ABC的面积尽可能的大,且∠ABC+∠ACB=60°,试问能否建一个满足要求的面积最大的户外健身区△ABC?若能,请求出△ABC面积的最大值,及此时⊙O的直径;若不能,请说明理由.
例2题图③
点D为BC中点
当点D为BC中点,参考(1)中作法,想到怎么作辅助线?
延长AD至点E,使DE=AD
△CDE≌△BDA
→S△ABC=S△AEC
S△AEC中,∠ACE=60°,AE为定值,参考(2)中作法,作△AEC的外接圆,求S△AEC最大值
E
点C在外接圆的直径上,且垂直AE时,S△AEC最大,此时△AEC为等边三角形
(3)能;
如解图③,延长AD至点E,使DE=AD=200 米,连接CE,易证△CDE≌△BDA,
∴∠DCE=∠CBA,S△ABC=S△AEC,
∵∠ABC+∠ACB=60°,∴∠ACE=60°,AE=400 米,
∴作△ACE的外接圆⊙P,连接CP、EP、DP,
则DP⊥AE,∠EPD=∠ECA=60°.
∴在Rt△PDE中,PD=200米,PE=400米,∴CP=EP=400米.
过点C作CH⊥AE于点H,
∵CH≤PC+PD=600米,∴当点D、H重合时,取等号,∴CHmax=600米,
解图③
解图④
∴S△AEC(max)= AE·CH=120000 平方米,
∴S△ABC(max)=120000 平方米.
当△ABC的面积最大时,
△ABC是等腰三角形,此时△AEC为等边三角形,
如解图④,连接AO,CO,在Rt△ADC中,AD=200 米,∠ACD=30°,
∴AC=400 米,∴OA=OC=400 米,
∴⊙O的直径为800 米.
综上所述,满足要求的户外健身区△ABC最大面积为120000 平方米,此时⊙O的直径为800 米.
课后小练
练习1 (2022陕西黑白卷)问题提出
(1)如图①,在四边形ABCD中,AB=AD,∠B与∠D互补,BC=2CD=20,点A到BC的距离为17,求四边形ABCD的面积;
练习1题图
解:(1)如解图①,连接AC,过点A作AH⊥BC于点H,将△ABH绕点A逆时针旋转,使得AB与AD重合,得到△ADG,∴∠B=∠ADG.
∵∠B与∠ADC互补,∴∠ADC+∠ADG=180°,
∴C,D,G三点共线.
∵点A到BC的距离为17,∴AH=17.
∵BC=2CD=20,∴CD=10.
由旋转的性质得△ADG≌△ABH,∴∠G=∠AHB=90°,AG=AH=17,
∴S△ACD= CD·AG= ×10×17=85,
S△ABC= BC·AH= ×20×17=170,
∴S四边形ABCD=S△ABC+S△ACD=170+85=255;
解题①
问题解决
(2)如图②,某公园计划在一块空地上修建两大主题活动区域,其中△ABE为健身活动区域,△CDE为文艺活动区域,已知AB=BC=60 m,∠B=60°,AB∥CD.按照设计要求,现要在BC上找一点E,使得AE=ED,∠AED=60°,请问是否存在满足设计要求的点E,使得文艺活动区域的面积尽可能大?若存在,求出文艺活动区域的面积及此时点B,E之间的距离;若不存在,请说明理由.
练习1题图
(2)存在.如解图②,连接AC,过点D作DF⊥BC交BC的延长线于点F.
∵AB=BC,∠B=60°,∴△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
又∵AE=ED,∠AED=60°,
∴△AED为等边三角形,∴AE=AD,∠EAD=60°.
∵∠BAE=∠BAC-∠EAC=60°-∠EAC,
∠CAD=∠EAD-∠EAC=60°-∠EAC,
∴∠BAE=∠CAD.
在△BAE和△CAD中, ,
∴△BAE≌△CAD(SAS),∴BE=CD=BC-EC=60-EC.
解题②
∵CD∥AB,
∴∠DCF=∠B=60°.
设CE=x,则BE=CD=60-x,
在Rt△DCF中,DF=DC·sin 60°=(60-x)× =30 - x,
∴S△ECD= CE·DF= x(30 - x)=- (x-30)2+225 ,
∵- <0,
∴当EC=30时,S△CDE有最大值,最大值为225 ,此时BE=60-x=30.
答:存在满足设计要求的点E,此时文艺活动区域的面积为225 m2,点B,E之间的距离为30 m.
解题②
练习2 (2022陕西预测卷)
(1)如图①,在平行四边形ABCD中,AB+BC=10,sinA= ,设AB=x,平行四边形ABCD的面积为y,求出y与x之间的函数表达式,并计算当x的值为多少时,y的值最大,且y的最大值为多少?
练习2题图
解:(1)如解图①,过点B作BE⊥AD交AD于点E,
在ABCD中,AB+BC=10,AD=BC,AB=x,则AD=10-x,
在Rt△ABE中,sin A= ,故BE=AB·sin A= x,
∴y=AD·BE=(10-x)× x=- x2+8x,
∵y=- x2+8x=- (x2-10x+25)+20=- (x-5)2+20,
∵- <0,0
解图①
(2)如图②,某商业规划用地的平面示意图为△ABC,规划局拟定在△ABC中规划出一片建筑群,其占地平面示意图为四边形AEDF,其中D为BC上一点,过点D分别作DE∥AC,DF∥AB,且点E、F分别在AB、AC上.经过实地测量后得知:∠BAC=60°,BC=600m,且点D为BC的三等分点(BD<CD),现要求建筑群所在的四边形AEDF的面积最大,请你通过论证并计算出建筑群(即四边形AEDF)所占面积最大为多少?
练习2题图
(2)由DE∥AC,DF∥AB可知:△EBD∽△ABC,△FDC∽△ABC,∴△ABC∽△EBD∽△FDC,
又∵点D为BC的三等分点,∴ ,
设S△ABC=x,则S△EBD= x,S△FDC= x,
故S四边形AEDF=S△ABC-S△EBD-S△FDC= x.
故当x最大时,四边形AEDF的面积最大.
如解图②,作△ABC的外接圆O,连接OA、OB、OC,并过点O作OG⊥BC,
过点A作AH⊥BC,
由∠BAC=60°,可知:∠BOC=120°,BG=GC=300 ,故OG=
=300,OB=2OG=600,
解图②
解图②
∵S△ABC= BC·AH=300 ·AH,AH≤OA+OG,
∴S△ABCmax=300 (OA+OG)=300 (600+300)=270000 ,
∴S四边形AEDFmax= ×270000 =120000 (m2),
即四边形AEDF所占面积最大为120000 m2.
同课章节目录
