2024陕西数学中考备考重难专题:综合与实践探究与证明课件 25张PPT
文档属性
| 名称 | 2024陕西数学中考备考重难专题:综合与实践探究与证明课件 25张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 14:33:35 | ||
图片预览






文档简介
(共25张PPT)
陕西 数学
综合与实践
2024中考备考重难专题课件
探究与证明
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
综合与实践
探究与证明
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 设问 解题关键点
2022 26 解 答 题 10 (1)求角的度数 (2)求四边形(不规则)的面积 (3)判断裁得的三角形部件是否符合要求,并证明结论 (1)等边三角形:“三线合一”
(2)四边形ACBP为菱形得到∠PBE=60°,∠ABC=30°
(3)由作法推出∠ACD=90°,PQ= AP
典例精讲
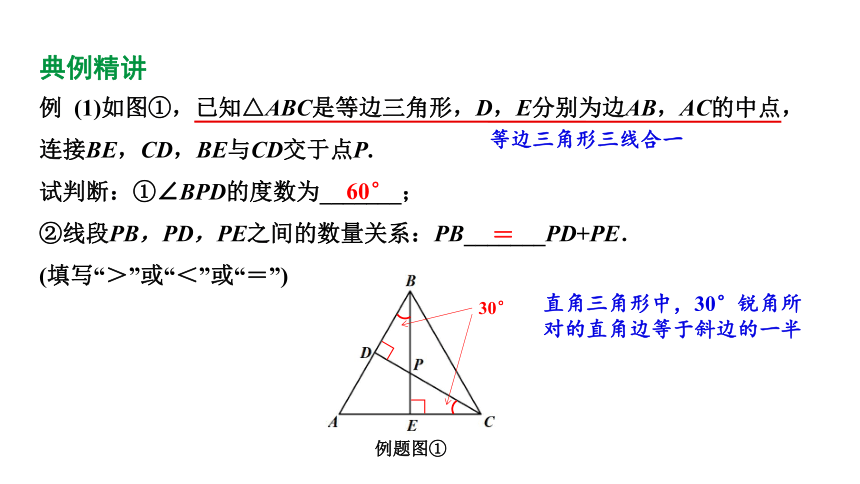
例 (1)如图①,已知△ABC是等边三角形,D,E分别为边AB,AC的中点,连接BE,CD,BE与CD交于点P.
试判断:①∠BPD的度数为_______;
②线段PB,PD,PE之间的数量关系:PB_______PD+PE.
(填写“>”或“<”或“=”)
例题图①
60°
=
等边三角形三线合一
∟
∟
30°
直角三角形中,30°锐角所对的直角边等于斜边的一半
典例精讲
(2)若点E是边AC所在射线AC上一动点(0按下列步骤画图:
①连接BE,作点A关于BE所在直线的对称点D,连接BD;
②作射线DC,交BE所在直线于点P;
小明所做的图形如图②所示,他猜想:PB=PD+PC.
下面是小明的思考过程:
例题图②
如图②,延长PD到F,使得DF=PC,连接BF.
发现△BPC≌△BFD,从而得到BP=BF,
又∵∠ABC=60°,∴可得∠PBF=60°,进而得到△PBF为等边三角形,从而得到线段PB,PC,PD之间关系是PB=PD+PC.
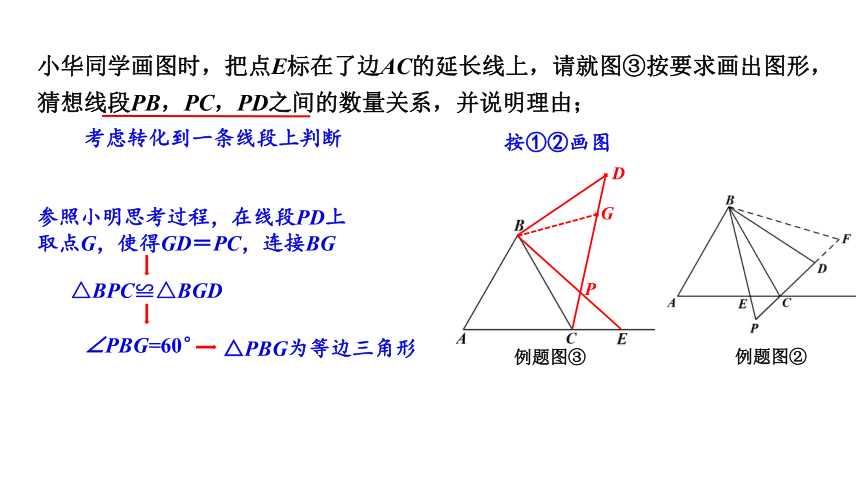
小华同学画图时,把点E标在了边AC的延长线上,请就图③按要求画出图形,猜想线段PB,PC,PD之间的数量关系,并说明理由;
例题图②
例题图③
.
D
P
.
G
按①②画图
参照小明思考过程,在线段PD上取点G,使得GD=PC,连接BG
考虑转化到一条线段上判断
△BPC≌△BGD
∠PBG=60°
△PBG为等边三角形
(2)画出图形如解图①,PD=PC+PB.
理由如下:如解图①,在线段PD上取点G,使得GD=PC,连接BG
∵△ABC是等边三角形,点A,D关于BE所在直线对称,
∴AB=BC=BD,∴∠D=∠BCP,∴△BPC≌△BGD(SAS),
∴BP=BG,∠CBP=∠DBG,
∵点A,D关于BE所在直线对称,
∴∠ABE=∠DBE,
∵∠ABC=60°,∴∠PBG=60°,
∴△PBG为等边三角形,
∴PD=DG+PG=PC+PB;
解图①
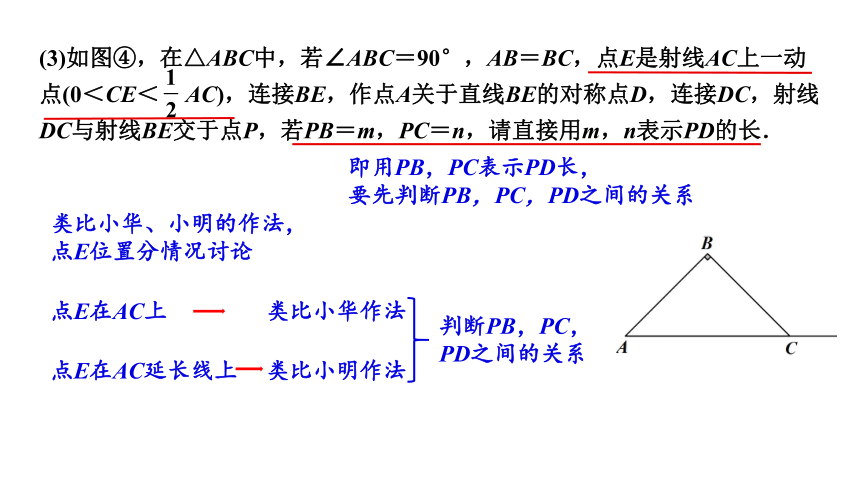
(3)如图④,在△ABC中,若∠ABC=90°,AB=BC,点E是射线AC上一动点(0<CE< AC),连接BE,作点A关于直线BE的对称点D,连接DC,射线DC与射线BE交于点P,若PB=m,PC=n,请直接用m,n表示PD的长.
即用PB,PC表示PD长,
要先判断PB,PC,PD之间的关系
类比小华、小明的作法,
点E位置分情况讨论
点E在AC上
点E在AC延长线上
类比小华作法
类比小明作法
判断PB,PC,PD之间的关系
【解法提示】当点E是线段AC上一点时,如解图②,延长PD到H,使得DH=PC,连接BH.
∵∠ABC=90°,AB=BC,点A,D关于BE所在直线对称,
∴AB=BC=BD,∴∠BCD=∠BDC,则∠BCP=∠BDH,
∴△BPC≌△BHD(SAS),
∴BP=BH,∠CBP=∠DBH,
∵点A,D关于BE所在直线对称,∴∠ABE=∠DBE,
∵∠ABC=90°,∴∠PBH=90°,∴△PBH为等腰直角三角形,
∴PH= PB,
∴PD=PH-DH= PB-PC,
∵PB=m,PC=n,
∴PD= m-n,
解图②
当点E是射线AC延长线上一点时,如解图③,在线段PD上取点I,使得DI=CP,连接BI,
同理可证△BPC≌△BID,△PBI为等腰直角三角形,
∴PI= PB,
∴PD=PI+DI= PB+PC,
∵PB=m,PC=n,
∴PD= m+n,
综上所述,PD的长为 m+n或 m-n.
解图③
课堂练兵
练习 (2023陕西真题子母卷)
(1)如图①,已知∠AOB,以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N,分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部交于点C,画射线OC,连接CM,CN,MN,则图①中与△OMC全等的是________;
练习题图①
OM=ON
MC=NC
△ONC
【解法提示】由题意可知,OM=ON,CM=CN,
又∵OC=OC,∴△OMC≌△ONC(SSS),
∴图①中与△OMC全等的是△ONC.
(2)如图②,在△ABC中,AD平分∠BAC,过点D作DM⊥AB于点M,连接CD,BD,若AB+AC=2AM,求证:∠ACD+∠ABD=180°;
练习题图②
∟
没有直接关联证明两角关系从条件入手试试吧
参照(1)中的全等三角形证明方法,作辅助线,过点D作DN⊥AC延长线于点N
N
Rt△ADN≌Rt△ADM(HL)
AN=AM
AM+MB+AN-CN=2AM
CN=BM
△CDN≌△BDM(SAS)
(2)证明:如解图①,过点D作DN⊥AC交AC的延长线于点N,
∵AD平分∠CAB,DN⊥AC,DM⊥AB,
∴DN=DM,
∵AD=AD,
∴Rt△ADN≌Rt△ADM(HL),∴AN=AM,
∵AB+AC=2AM,
∴AM+MB+AN-CN=2AM,即CN=BM,
∵∠DNC=∠DMB=90°,DN=DM,
∴△CDN≌△BDM(SAS),
∴∠DCN=∠ABD,∴∠ACD+∠ABD=∠ACD+∠DCN=180°;
解图①
(3)如图③,工人刘师傅有一块三角形铁板ABC,∠B=60°,他需要利用铁板的边角裁出一个四边形BEFD,并要求∠EFD=120°,EF=DF.刘师傅先在纸稿上画出了三角形铁板的草图,再用尺规作出∠BAC的平分线AD交BC于点D,作∠BCA的平分线CE交AB于点E,AD,CE交于点F,得到四边形BEFD. 请问,若按上述作法,裁得的四边形BEFD是否符合要求?请证明你的结论.
练习题图③
60°
参照(1)(2)方法作辅助线,过点F分别向AB,BC,AC边作垂线
FG=FH=FK
∠GFH=120°
∠EFD=∠AFC=120°
∠AFC=120°
∠EFG=∠DFH
FG=FH
FG⊥AB,FH⊥BC
△EFG≌△DFH
G
H
K
(3)解:符合要求,
证明:如解图②,过点F分别作FG⊥AB于点G,
作FH⊥BC于点H,作FK⊥AC于点K,
∵AD,CE分别是∠BAC,∠BCA的平分线,∴FG=FH=FK,
∵∠B=60°,
∴在四边形BGFH中,∠GFH=360°-60°-90°×2=120°,
∠FAC+∠FCA=(180°-60°)=60°,
在△AFC中,∠AFC=180°-(∠FAC+∠FCA)=180°-60°=120°,
∴∠EFD=∠AFC=120°=∠GFH,
∴∠EFG=∠DFH,
解图②
在△EFG和△DFH中,
∴△EFG≌△DFH(ASA),
∴FE=FD.
∴裁得的四边形BEFD符合要求.
解图②
课后小练
练习 (2022陕西真题)问题提出
(1)如图①,AD是等边△ABC的中线,点P在AD的延长线上,且AP=AC,则∠APC的度数为____;
75°
【解法提示】∵AP是等边△ABC的中线,∴∠PAC= ∠BAC=30°,
又∵AP=AC,
∴∠APC= (180°-∠PAC)=75°.
练习题图①
问题探究
(2)如图②,在△ABC中,CA=CB=6,∠C=120°.过点A作AP∥BC,且AP=BC,过点P作直线l⊥BC,分别交AB、BC于点O、E,求四边形OECA的面积;
练习题图②
(2)如解图①,连接BP.
∵AP∥BC,AP=BC=AC,
∴四边形ACBP是菱形,
∴BP=AC=6.
∵∠ACB=120°,∴∠PBE=60°.
∵l⊥BC,
∴BE=BP·cos 60°=3,PE=BP·sin 60°=3 ,
解图①
∴S△ABC= BC·PE=9 .
∵∠C=120°,CA=CB,
∴∠ABC=30°,
∴OE=BE·tan 30°= ,
∴S△OBE= BE·OE= ,
∴S四边形OECA=S△ABC-S△OBE= ;
解图①
【一题多解】如解图②,连接OC,
∵BC=AC=6,∠ACB=120°,
∴∠ABC=∠BAC=30°.
∵AP∥BC,PE⊥BC,∴∠PAB=30°,∠EPA=90°,
又∵AP=BC=AC,AO=AO,
∴△PAO≌△CAO,∴∠OCA=∠OPA=90°,
∴∠OCB=30°,∴OB=OC,
∴EC=3,OE= ,OC=2 ,
∴S△EOC= OE·EC= ,S△AOC= OC·AC=6 ,
∴S四边形OECA=S△AOC+S△EOC= .
解图②
问题解决
(3)如图③,现有一块△ABC型板材,∠ACB为钝角,∠BAC=45°.工人师傅想用这块板材裁出一个△ABP型部件,并要求∠BAP=15°,AP=AC.工人师傅在这块板材上的作法如下:
①以点C为圆心,以CA长为半径画弧,交AB于点D,连接CD;
②作CD的垂直平分线l,与CD交于点E;
③以点A为圆心,以AC长为半径画弧,交直线l于点P,
连接AP、BP,得△ABP.
请问,若按上述作法,
裁得的△ABP型部件是否符合要求?请证明你的结论.
练习题图③
(3)符合要求.
证明:如解图③,过点P作PQ⊥AC交AC于点Q,由作法可知,AP=AC,
∵CD=CA,∠BAC=45°,
∴∠ACD=90°,
∵直线l垂直平分DC,
∴PQ=EC= CD= AC= AP,
∴∠PAQ=30°,
∴∠BAP=∠BAC-∠PAQ=45°-30°=15°,
∴裁得的△ABP型部件符合要求.
解图③
【一题多解】解法一:
符合要求.
证明:由作法知AP=AC.
∵CD=CA,∠CAB=45°,∴∠ACD=90°.
如解图④,以AC,CD为边,作正方形ACDF,连接PF.
∴AF=AC=AP,∠CAF=90°.
∵l是CD的垂直平分线,
∴l是AF的垂直平分线.
∴PF=PA,∴△AFP为等边三角形,
∴∠FAP=60°,∴∠PAC=30°,∴∠BAP=15°.
∴裁得的△ABP型部件符合要求.
解图④
解法二:符合要求.
证明:如解图⑤,过点A作AN⊥EP交EP的延长线于点N,EN交AD于点M,
由作法知CD=CA=AP,∵∠BAC=45°,
∴∠ACD=90°,
又∵AN⊥EP,EP⊥CD,
∴四边形ACEN为矩形,
∴AN∥CE,AN=CE= CD= AC= AP,
∴∠DAN=∠ADC=45°,∠NAP=60°,
∴∠BAP=∠NAP-∠DAN=60°-45°=15°,
∴裁得的△ABP型部件符合要求.
解图⑤
陕西 数学
综合与实践
2024中考备考重难专题课件
探究与证明
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
综合与实践
探究与证明
课堂练兵
课后小练
1
典例精讲
2
3
考情分析
年份 题号 题型 分值 设问 解题关键点
2022 26 解 答 题 10 (1)求角的度数 (2)求四边形(不规则)的面积 (3)判断裁得的三角形部件是否符合要求,并证明结论 (1)等边三角形:“三线合一”
(2)四边形ACBP为菱形得到∠PBE=60°,∠ABC=30°
(3)由作法推出∠ACD=90°,PQ= AP
典例精讲
例 (1)如图①,已知△ABC是等边三角形,D,E分别为边AB,AC的中点,连接BE,CD,BE与CD交于点P.
试判断:①∠BPD的度数为_______;
②线段PB,PD,PE之间的数量关系:PB_______PD+PE.
(填写“>”或“<”或“=”)
例题图①
60°
=
等边三角形三线合一
∟
∟
30°
直角三角形中,30°锐角所对的直角边等于斜边的一半
典例精讲
(2)若点E是边AC所在射线AC上一动点(0
①连接BE,作点A关于BE所在直线的对称点D,连接BD;
②作射线DC,交BE所在直线于点P;
小明所做的图形如图②所示,他猜想:PB=PD+PC.
下面是小明的思考过程:
例题图②
如图②,延长PD到F,使得DF=PC,连接BF.
发现△BPC≌△BFD,从而得到BP=BF,
又∵∠ABC=60°,∴可得∠PBF=60°,进而得到△PBF为等边三角形,从而得到线段PB,PC,PD之间关系是PB=PD+PC.
小华同学画图时,把点E标在了边AC的延长线上,请就图③按要求画出图形,猜想线段PB,PC,PD之间的数量关系,并说明理由;
例题图②
例题图③
.
D
P
.
G
按①②画图
参照小明思考过程,在线段PD上取点G,使得GD=PC,连接BG
考虑转化到一条线段上判断
△BPC≌△BGD
∠PBG=60°
△PBG为等边三角形
(2)画出图形如解图①,PD=PC+PB.
理由如下:如解图①,在线段PD上取点G,使得GD=PC,连接BG
∵△ABC是等边三角形,点A,D关于BE所在直线对称,
∴AB=BC=BD,∴∠D=∠BCP,∴△BPC≌△BGD(SAS),
∴BP=BG,∠CBP=∠DBG,
∵点A,D关于BE所在直线对称,
∴∠ABE=∠DBE,
∵∠ABC=60°,∴∠PBG=60°,
∴△PBG为等边三角形,
∴PD=DG+PG=PC+PB;
解图①
(3)如图④,在△ABC中,若∠ABC=90°,AB=BC,点E是射线AC上一动点(0<CE< AC),连接BE,作点A关于直线BE的对称点D,连接DC,射线DC与射线BE交于点P,若PB=m,PC=n,请直接用m,n表示PD的长.
即用PB,PC表示PD长,
要先判断PB,PC,PD之间的关系
类比小华、小明的作法,
点E位置分情况讨论
点E在AC上
点E在AC延长线上
类比小华作法
类比小明作法
判断PB,PC,PD之间的关系
【解法提示】当点E是线段AC上一点时,如解图②,延长PD到H,使得DH=PC,连接BH.
∵∠ABC=90°,AB=BC,点A,D关于BE所在直线对称,
∴AB=BC=BD,∴∠BCD=∠BDC,则∠BCP=∠BDH,
∴△BPC≌△BHD(SAS),
∴BP=BH,∠CBP=∠DBH,
∵点A,D关于BE所在直线对称,∴∠ABE=∠DBE,
∵∠ABC=90°,∴∠PBH=90°,∴△PBH为等腰直角三角形,
∴PH= PB,
∴PD=PH-DH= PB-PC,
∵PB=m,PC=n,
∴PD= m-n,
解图②
当点E是射线AC延长线上一点时,如解图③,在线段PD上取点I,使得DI=CP,连接BI,
同理可证△BPC≌△BID,△PBI为等腰直角三角形,
∴PI= PB,
∴PD=PI+DI= PB+PC,
∵PB=m,PC=n,
∴PD= m+n,
综上所述,PD的长为 m+n或 m-n.
解图③
课堂练兵
练习 (2023陕西真题子母卷)
(1)如图①,已知∠AOB,以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N,分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部交于点C,画射线OC,连接CM,CN,MN,则图①中与△OMC全等的是________;
练习题图①
OM=ON
MC=NC
△ONC
【解法提示】由题意可知,OM=ON,CM=CN,
又∵OC=OC,∴△OMC≌△ONC(SSS),
∴图①中与△OMC全等的是△ONC.
(2)如图②,在△ABC中,AD平分∠BAC,过点D作DM⊥AB于点M,连接CD,BD,若AB+AC=2AM,求证:∠ACD+∠ABD=180°;
练习题图②
∟
没有直接关联证明两角关系从条件入手试试吧
参照(1)中的全等三角形证明方法,作辅助线,过点D作DN⊥AC延长线于点N
N
Rt△ADN≌Rt△ADM(HL)
AN=AM
AM+MB+AN-CN=2AM
CN=BM
△CDN≌△BDM(SAS)
(2)证明:如解图①,过点D作DN⊥AC交AC的延长线于点N,
∵AD平分∠CAB,DN⊥AC,DM⊥AB,
∴DN=DM,
∵AD=AD,
∴Rt△ADN≌Rt△ADM(HL),∴AN=AM,
∵AB+AC=2AM,
∴AM+MB+AN-CN=2AM,即CN=BM,
∵∠DNC=∠DMB=90°,DN=DM,
∴△CDN≌△BDM(SAS),
∴∠DCN=∠ABD,∴∠ACD+∠ABD=∠ACD+∠DCN=180°;
解图①
(3)如图③,工人刘师傅有一块三角形铁板ABC,∠B=60°,他需要利用铁板的边角裁出一个四边形BEFD,并要求∠EFD=120°,EF=DF.刘师傅先在纸稿上画出了三角形铁板的草图,再用尺规作出∠BAC的平分线AD交BC于点D,作∠BCA的平分线CE交AB于点E,AD,CE交于点F,得到四边形BEFD. 请问,若按上述作法,裁得的四边形BEFD是否符合要求?请证明你的结论.
练习题图③
60°
参照(1)(2)方法作辅助线,过点F分别向AB,BC,AC边作垂线
FG=FH=FK
∠GFH=120°
∠EFD=∠AFC=120°
∠AFC=120°
∠EFG=∠DFH
FG=FH
FG⊥AB,FH⊥BC
△EFG≌△DFH
G
H
K
(3)解:符合要求,
证明:如解图②,过点F分别作FG⊥AB于点G,
作FH⊥BC于点H,作FK⊥AC于点K,
∵AD,CE分别是∠BAC,∠BCA的平分线,∴FG=FH=FK,
∵∠B=60°,
∴在四边形BGFH中,∠GFH=360°-60°-90°×2=120°,
∠FAC+∠FCA=(180°-60°)=60°,
在△AFC中,∠AFC=180°-(∠FAC+∠FCA)=180°-60°=120°,
∴∠EFD=∠AFC=120°=∠GFH,
∴∠EFG=∠DFH,
解图②
在△EFG和△DFH中,
∴△EFG≌△DFH(ASA),
∴FE=FD.
∴裁得的四边形BEFD符合要求.
解图②
课后小练
练习 (2022陕西真题)问题提出
(1)如图①,AD是等边△ABC的中线,点P在AD的延长线上,且AP=AC,则∠APC的度数为____;
75°
【解法提示】∵AP是等边△ABC的中线,∴∠PAC= ∠BAC=30°,
又∵AP=AC,
∴∠APC= (180°-∠PAC)=75°.
练习题图①
问题探究
(2)如图②,在△ABC中,CA=CB=6,∠C=120°.过点A作AP∥BC,且AP=BC,过点P作直线l⊥BC,分别交AB、BC于点O、E,求四边形OECA的面积;
练习题图②
(2)如解图①,连接BP.
∵AP∥BC,AP=BC=AC,
∴四边形ACBP是菱形,
∴BP=AC=6.
∵∠ACB=120°,∴∠PBE=60°.
∵l⊥BC,
∴BE=BP·cos 60°=3,PE=BP·sin 60°=3 ,
解图①
∴S△ABC= BC·PE=9 .
∵∠C=120°,CA=CB,
∴∠ABC=30°,
∴OE=BE·tan 30°= ,
∴S△OBE= BE·OE= ,
∴S四边形OECA=S△ABC-S△OBE= ;
解图①
【一题多解】如解图②,连接OC,
∵BC=AC=6,∠ACB=120°,
∴∠ABC=∠BAC=30°.
∵AP∥BC,PE⊥BC,∴∠PAB=30°,∠EPA=90°,
又∵AP=BC=AC,AO=AO,
∴△PAO≌△CAO,∴∠OCA=∠OPA=90°,
∴∠OCB=30°,∴OB=OC,
∴EC=3,OE= ,OC=2 ,
∴S△EOC= OE·EC= ,S△AOC= OC·AC=6 ,
∴S四边形OECA=S△AOC+S△EOC= .
解图②
问题解决
(3)如图③,现有一块△ABC型板材,∠ACB为钝角,∠BAC=45°.工人师傅想用这块板材裁出一个△ABP型部件,并要求∠BAP=15°,AP=AC.工人师傅在这块板材上的作法如下:
①以点C为圆心,以CA长为半径画弧,交AB于点D,连接CD;
②作CD的垂直平分线l,与CD交于点E;
③以点A为圆心,以AC长为半径画弧,交直线l于点P,
连接AP、BP,得△ABP.
请问,若按上述作法,
裁得的△ABP型部件是否符合要求?请证明你的结论.
练习题图③
(3)符合要求.
证明:如解图③,过点P作PQ⊥AC交AC于点Q,由作法可知,AP=AC,
∵CD=CA,∠BAC=45°,
∴∠ACD=90°,
∵直线l垂直平分DC,
∴PQ=EC= CD= AC= AP,
∴∠PAQ=30°,
∴∠BAP=∠BAC-∠PAQ=45°-30°=15°,
∴裁得的△ABP型部件符合要求.
解图③
【一题多解】解法一:
符合要求.
证明:由作法知AP=AC.
∵CD=CA,∠CAB=45°,∴∠ACD=90°.
如解图④,以AC,CD为边,作正方形ACDF,连接PF.
∴AF=AC=AP,∠CAF=90°.
∵l是CD的垂直平分线,
∴l是AF的垂直平分线.
∴PF=PA,∴△AFP为等边三角形,
∴∠FAP=60°,∴∠PAC=30°,∴∠BAP=15°.
∴裁得的△ABP型部件符合要求.
解图④
解法二:符合要求.
证明:如解图⑤,过点A作AN⊥EP交EP的延长线于点N,EN交AD于点M,
由作法知CD=CA=AP,∵∠BAC=45°,
∴∠ACD=90°,
又∵AN⊥EP,EP⊥CD,
∴四边形ACEN为矩形,
∴AN∥CE,AN=CE= CD= AC= AP,
∴∠DAN=∠ADC=45°,∠NAP=60°,
∴∠BAP=∠NAP-∠DAN=60°-45°=15°,
∴裁得的△ABP型部件符合要求.
解图⑤
同课章节目录
