2024陕西数学中考备考重难专题:综合与实践线段最值课件 30张PPT
文档属性
| 名称 | 2024陕西数学中考备考重难专题:综合与实践线段最值课件 30张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 14:37:29 | ||
图片预览







文档简介
(共30张PPT)
陕西 数学
综合与实践
2024中考备考重难专题课件
线段最值
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
综合与实践
线段最值
课堂练兵
课后小练
1
典例精讲
2
3
年份 题号 题型 分值 最值的方法 设问 解题关键点
2020 25 解 答 题 12 “将军饮马” (1)求三角形外接圆半径 (2)求线段最大值(点圆最值) (3)求三条线段和的最小值(“一定两动”) (1)三角形外接圆的性质:圆心到三个顶点的距离相等,等腰三角形三线合一
(2)P、O、M三点共线,且位于圆心异侧时,PM值大值(点圆最值)
(3)根据“将军饮马”作对称转化到一条线段,再利用三点共线线段最短
考情分析
年份 题号 题型 分值 最值的方法 设问 解题关键点
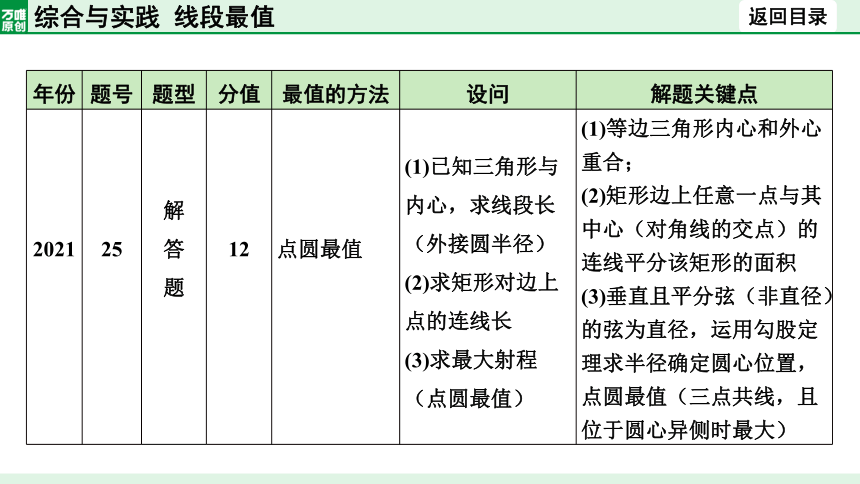
2021 25 解 答 题 12 点圆最值 (1)已知三角形与内心,求线段长(外接圆半径) (2)求矩形对边上点的连线长 (3)求最大射程(点圆最值) (1)等边三角形内心和外心重合;
(2)矩形边上任意一点与其中心(对角线的交点)的连线平分该矩形的面积
(3)垂直且平分弦(非直径)的弦为直径,运用勾股定理求半径确定圆心位置,点圆最值(三点共线,且位于圆心异侧时最大)
年份 题号 题型 分值 最值的方法 设问 解题关键点
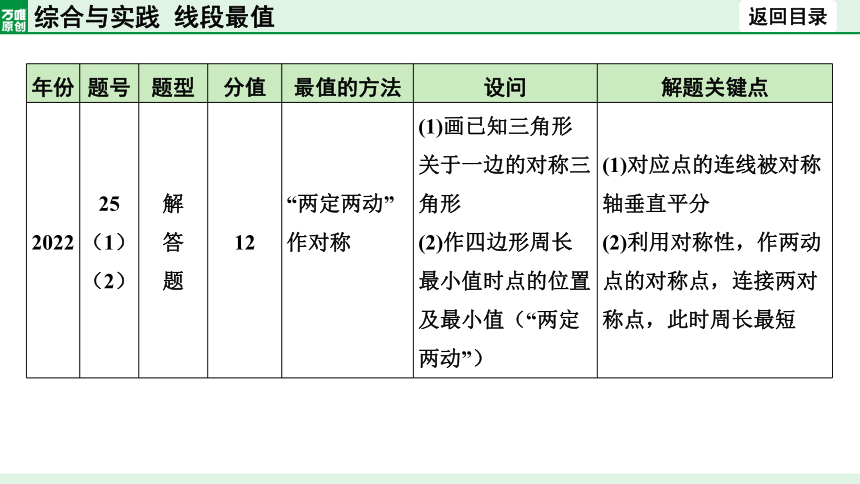
2022 25(1)(2) 解 答 题 12 “两定两动”作对称 (1)画已知三角形关于一边的对称三角形 (2)作四边形周长最小值时点的位置及最小值(“两定两动”)
(1)对应点的连线被对称轴垂直平分
(2)利用对称性,作两动点的对称点,连接两对称点,此时周长最短
年份 题号 题型 分值 最值的方法 设问 解题关键点
2023 25(2) 解 答 题 12 垂线段最短 (2)求三角形周长的最小值 (2)作对称点,转化为线段长
典例精讲
例 (2022陕西逆袭卷)问题提出
(1)如图①,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,对角线AC=6,若将△ABC绕着点A逆时针旋转60°得到△ADE,求BC+CD的值;
例题图①
可知旋转后AB边和AD边重合
BC+CD=DE+CD=CE
AC=AE
旋转60°→∠CAE=60°
△ACE为等边三角形
可以直接表示成BC+CD=DE+CD=CE吗?
解:(1)∵将△ABC绕着点A逆时针旋转60°得到△ADE,
∴DE=BC,AE=AC=6,∠ADE=∠ABC,∠DAE=∠BAC,
∵∠BAD=∠BAC+∠CAD=60°,∠BCD=120°,
∴∠CAE=∠CAD+∠DAE=60°,∠ADC+∠ABC=180°,
∴∠ADC+∠ADE=180°,
∴E,D,C三点共线.
∴△ACE是等边三角形,
∴CE=AC=6,
∴BC+CD=DE+CD=CE=6;
例题图①
问题探究
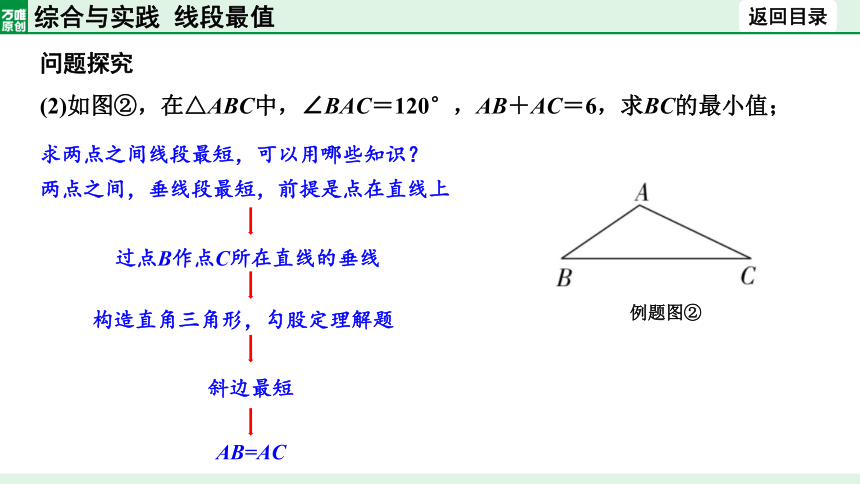
(2)如图②,在△ABC中,∠BAC=120°,AB+AC=6,求BC的最小值;
例题图②
求两点之间线段最短,可以用哪些知识?
两点之间,垂线段最短,前提是点在直线上
过点B作点C所在直线的垂线
构造直角三角形,勾股定理解题
斜边最短
AB=AC
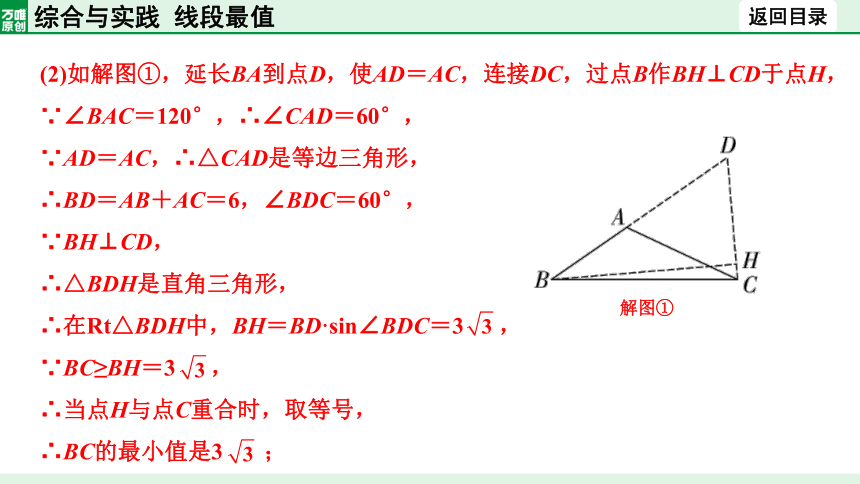
(2)如解图①,延长BA到点D,使AD=AC,连接DC,过点B作BH⊥CD于点H,
∵∠BAC=120°,∴∠CAD=60°,
∵AD=AC,∴△CAD是等边三角形,
∴BD=AB+AC=6,∠BDC=60°,
∵BH⊥CD,
∴△BDH是直角三角形,
∴在Rt△BDH中,BH=BD·sin∠BDC=3 ,
∵BC≥BH=3 ,
∴当点H与点C重合时,取等号,
∴BC的最小值是3 ;
解图①
问题解决
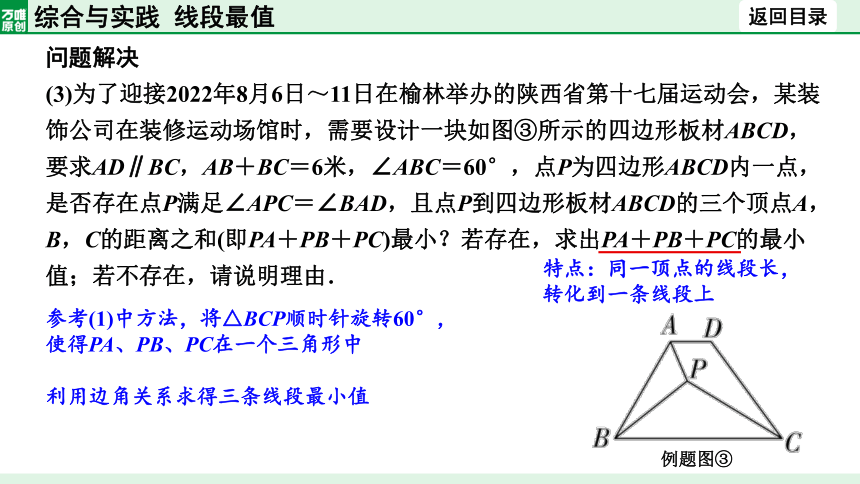
(3)为了迎接2022年8月6日~11日在榆林举办的陕西省第十七届运动会,某装饰公司在装修运动场馆时,需要设计一块如图③所示的四边形板材ABCD,要求AD∥BC,AB+BC=6米,∠ABC=60°,点P为四边形ABCD内一点,是否存在点P满足∠APC=∠BAD,且点P到四边形板材ABCD的三个顶点A,B,C的距离之和(即PA+PB+PC)最小?若存在,求出PA+PB+PC的最小值;若不存在,请说明理由.
例题图③
特点:同一顶点的线段长,转化到一条线段上
参考(1)中方法,将△BCP顺时针旋转60°,使得PA、PB、PC在一个三角形中
利用边角关系求得三条线段最小值
(3)存在.
如解图②,将△BCP绕着点B顺时针旋转60°后得到△BEF,连接PF,AE,
则EF=CP,△BPF为等边三角形,
∴PF=BP,∴PA+PB+PC=PA+PF+EF≥AE,
∴当A,P,F,E四点共线时,取等号,
∴PA+PB+PC的最小值为AE的长.
延长AB到点G,使BG=BC,连接GE,
由旋转的性质得BE=BC,∠CBE=60°,∴BG=BE,
∵∠ABC=60°,∴∠GBE=60°,
∴△BEG为等边三角形,∴∠BGE=60°,AG=AB+BC=6.
解图②
过点A作AH⊥GE于点H,
∴在Rt△AGH中,AH=AG·sin∠BGE=3 ,
∵AE≥AH=3 ,∴如解图③,当点H与点E重合时,取等号,
∴AE的最小值=3 ,∴PA+PB+PC的最小值=AE的最小值=3 .
∵△BPF是等边三角形,
∴∠BPF=∠BFP=60°,∴∠APB=∠BFE=120°,
由旋转的性质得∠BPC=∠BFE,
∴∠APB=∠BPC=120°,∴∠APC=120°,
∵AD∥BC,∠ABC=60°,∴∠BAD=120°,
∴∠APC=∠BAD.∴存在满足条件的点P,且PA+PB+PC的最小值为3 米.
解图③
练习 (2022陕西预测卷)
问题提出
(1)如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,若延长CD到点E, 使ED=BC,连接AE,得到△ADE≌△ABC,则AC与AE的位置关系是________,数量关系是________;
练习题图
课堂练兵
猜想:位置关系:垂直,数量关系:相等
△ADE≌△ABC
ED=BC
∠EAD=∠CAB
AE=AC
∠BAD=90°
∠BAC=90°
垂直
相等
问题探究
(2)如图②,已知等边△ABC内接于⊙O,P为 上一点,连接AP,BP,CP.若BP=4,求AP+CP的值;
练习题图②
考虑转化到一条线段上
参考(1)中的作法,延长PA,使得AD=PC,连接CB
作辅助线
得全等三角形
依据边角关系求线段和
△ADB≌△CPB
△BPD是等边三角形
DP=AP+AD(PC)=BP
D
解图①
(2)如解图①,延长PA到点D,使AD=CP,连接BD,则△ADB≌△CPB,
∴BD=BP,
∵∠BPD=∠BCA=60°,
∴△BPD是等边三角形,
∴DP=BP=4,
又∵DP=AP+AD=AP+CP,
∴AP+CP=4;
问题解决
(3)有一个直径为80cm的圆形板材⊙O,如图③所示.现需在该板材上裁出一
个四边形ABCD的部件,要求对角线AC平分∠BAD,BD=40 cm,CD=40
cm,并使裁出的四边形ABCD部件的周长最大.试问,是否存在符合要求的周长最大的四边形ABCD部件?若存在,请求出四边形ABCD部件周长的最大值;若不存在,请说明理由.
练习题图③
BC=CD=40cm
BC=CD为定值,
四边形ABCD周长最大
即求AB+AD值最大
作辅助线延长AB到点E,使BE=AD,连接CE
题意可得△ACE∽△DCB
当AC取最大值
AE就有最大值
?
AC为直径取最大
E
(3)存在;
如解图②,延长AB到点E,使BE=AD,连接CE,则△BEC≌△DAC,
∴CE=AC,∠ECB=∠ACD,
∴∠ACE=∠DCB,
又∵∠BAC=∠BDC,
∴△ACE∽△DCB,∴ ,
又∵AC平分∠BAD,∴ ,
∴BC=CD=40cm,即 ,
∴AE= AC,
当AC取最大值时,AE就有最大值.
解图②
解图②
连接OA,OC,
∵AC≤OA+OC=80,∴当点C,O,A共线时,取等号,
∴ACmax=80cm,∴AEmax=80 cm,
又∵AE=AB+BE=AB+AD,∴AB+AD的最大值是80 cm,
∴C四边形ABCD(max)=80( +1)cm,
∴存在符合要求的周长最大的四边形ABCD部件,
其最大值为80( +1)cm.
练习1 (2023陕西预测卷)问题提出
(1)如图①,已知△ABC,试在AB上确定一点P,连接CP,使CP平分S△ABC;
练习1题图①
解:(1)如解图①所示,点P即为所求;
解图①
课后小练
(2)问题探究
如图②,在△ABC中,AD是△ABC的角平分线,求证: ;
练习1题图②
(2)如解图②,过点D分别作DE⊥AC于点E,DF⊥AB
于点F,过点A作AM⊥BC于点M.
∵AD是△ABC的角平分线,∴DE=DF,
∵S△ABD= ×AB·DF= ×BD·AM,
S△ACD= ×AC·DE= ×CD·AM,
∴ ,∴ ;
解图②
(3)问题解决
如图③,某城市想依托原有废旧机车工厂留存的机车铁轨AP改造新的机车主题公园△ABC,点P在BC上,且AP将新的主题公园分为面积相等的两个主题活动区.该项目负责人计划在AB,AC的中点E,F上放置各种年代的机车头作为群众拍照打卡地标,并使得两地标之间距离最大,即EF最大,已知∠BAC=120°,AP=100m.请问是否存在符合要求的△ABC?若存在,请求出EF的最大值;若不存在,请说明理由.
练习题图③
(3)存在.
如解图③,延长AP至点M,使得PM=AP,连接CM,则△CPM≌△BPA,
∴∠ABP=∠MCP,∴AB∥CM,
∵∠BAC=120°,∴∠ACM=60°,
∴点C在以AM为弦,其所对圆周角为60°的圆弧上运动,圆弧的圆心为点O,
∵点E,F分别是AB,AC的中点,
∴EF是△ABC的中位线,∴EF= BC,
∴BC最大时,EF最大,
∵点P为BC的中点,
∴BC=2CP,即CP最大时,BC最大,
解图③
解图③
∴PC最大时,EF最大,EF= BC= ×2PC=PC,
当C,O,P三点共线,即点C位于点C′处时,PC最大,即为PC′,此时△AC′M为等边三角形,
∴PC′=AP·tan60°=100 ,
∴PC的最大值为100 ,∴EF的最大值为100 m.
练习2 (2022陕西黑白卷)问题提出
(1)如图①,在Rt△ABC中,∠ABC=90°,AB=3,BC=6,求Rt△ABC外接圆的半径;
练习2题图①
解:(1)∵∠ABC=90°,AB=3,
BC=6,
∴AC= ,
∴Rt△ABC外接圆的半径为 AC= ;
问题解决
(2)如图②,某园林规划局计划在一片空地上开垦出一片区域ABCD,用于种植珍稀树苗,且用栅栏保护.其中四边形ABCD为平行四边形,连接AC,BM平分∠ABC交AC于点M,BM=40 m,∠ABC=60°.为了尽可能地减少栅栏地使用,需使四边形ABCD的周长最小,你认为该园林规划局的想法能否实现?若能,请求出四边形ABCD周长的最小值;若不能,请说明理由.
练习2题图②
(2)能实现.
如解图①,过点M作ME⊥AB于点E,MF⊥BC于点F,
∵∠ABC=60°,BM平分∠ABC,
∴∠EBM=∠FBM=30°,∴△BEM≌△BFM,
∴BE=BF= BM=20 ,ME=MF= BM=20.
∵四边形ABCD是平行四边形,
∴C ABCD=2(AB+BC)=2(BE+AE+BF+CF).
∵BE=BF=20 ,
∴要使得四边形ABCD的周长最小,即AE+CF最小.
解图①
∵在四边形EBFM中,∠EBF=60°,
∴∠EMF=120°,∴∠AME+∠FMC=60°.
将△AME绕点M逆时针旋转,使得ME与MF重合,得到△A′MF,
由旋转的性质可得,EA=A′F,∠AME=∠A′MF,
∴∠A′MF+∠FMC=60°.
∵∠AEM=∠CFM=90°,∴∠A′FM+∠CFM=180°.
∴A′,F,C三点共线,
∴AE+CF=A′F+CF=A′C,
∴AE+CF的最小值即为A′C的最小值.
在△MA′C中,∠A′MC=60°,MF=20.
解图①
如解图②,作△MA′C的外接圆⊙G,连接GM,GA′,GC,过点G作GH⊥A′C于点H,
∴∠A′GC=2∠A′MC=120°.
∵A′G=CG,∴∠GA′C=∠GCA′=30°,
∴GH= A′G= GM,A′C=2× A′G= GM.
∵GM+GH≥MF,∴GM+ GM≥MF,
即 GM≥20,∴GM≥ ,
∴A′C= GM≥ ,∴A′C的最小值为 ,
∴C ABCD=2(BE+AE+BF+CF)≥2×(20 +20 + )= m.
即四边形ABCD周长的最小值为 m.
解图②
陕西 数学
综合与实践
2024中考备考重难专题课件
线段最值
课件说明
一、课件设计初衷
基于老师在总复习过程中对重难题型有较大的需求,以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性,有助于学生题图结合梳理题意,理解平面图形的变化过程.
二、课件亮点
1.依据区域考情,针对性选题
按照本地区考情及考法选题,针对性强,有效提高老师备课效率
2.贴近学生实际解题情境,形式符合教学习惯
审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注,帮助学生梳理关键信息,激发学生兴趣,调动积极性
3.含解题思路引导与方法总结,提高课堂互动性
通过问题启发式解题思路点拨,激发学生数学思考与探索. 方法总结使学生复习一类题,会一类题,取得有效的复习成果
三、课件使用场景
适用于中考专题复习或题位复习
综合与实践
线段最值
课堂练兵
课后小练
1
典例精讲
2
3
年份 题号 题型 分值 最值的方法 设问 解题关键点
2020 25 解 答 题 12 “将军饮马” (1)求三角形外接圆半径 (2)求线段最大值(点圆最值) (3)求三条线段和的最小值(“一定两动”) (1)三角形外接圆的性质:圆心到三个顶点的距离相等,等腰三角形三线合一
(2)P、O、M三点共线,且位于圆心异侧时,PM值大值(点圆最值)
(3)根据“将军饮马”作对称转化到一条线段,再利用三点共线线段最短
考情分析
年份 题号 题型 分值 最值的方法 设问 解题关键点
2021 25 解 答 题 12 点圆最值 (1)已知三角形与内心,求线段长(外接圆半径) (2)求矩形对边上点的连线长 (3)求最大射程(点圆最值) (1)等边三角形内心和外心重合;
(2)矩形边上任意一点与其中心(对角线的交点)的连线平分该矩形的面积
(3)垂直且平分弦(非直径)的弦为直径,运用勾股定理求半径确定圆心位置,点圆最值(三点共线,且位于圆心异侧时最大)
年份 题号 题型 分值 最值的方法 设问 解题关键点
2022 25(1)(2) 解 答 题 12 “两定两动”作对称 (1)画已知三角形关于一边的对称三角形 (2)作四边形周长最小值时点的位置及最小值(“两定两动”)
(1)对应点的连线被对称轴垂直平分
(2)利用对称性,作两动点的对称点,连接两对称点,此时周长最短
年份 题号 题型 分值 最值的方法 设问 解题关键点
2023 25(2) 解 答 题 12 垂线段最短 (2)求三角形周长的最小值 (2)作对称点,转化为线段长
典例精讲
例 (2022陕西逆袭卷)问题提出
(1)如图①,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,对角线AC=6,若将△ABC绕着点A逆时针旋转60°得到△ADE,求BC+CD的值;
例题图①
可知旋转后AB边和AD边重合
BC+CD=DE+CD=CE
AC=AE
旋转60°→∠CAE=60°
△ACE为等边三角形
可以直接表示成BC+CD=DE+CD=CE吗?
解:(1)∵将△ABC绕着点A逆时针旋转60°得到△ADE,
∴DE=BC,AE=AC=6,∠ADE=∠ABC,∠DAE=∠BAC,
∵∠BAD=∠BAC+∠CAD=60°,∠BCD=120°,
∴∠CAE=∠CAD+∠DAE=60°,∠ADC+∠ABC=180°,
∴∠ADC+∠ADE=180°,
∴E,D,C三点共线.
∴△ACE是等边三角形,
∴CE=AC=6,
∴BC+CD=DE+CD=CE=6;
例题图①
问题探究
(2)如图②,在△ABC中,∠BAC=120°,AB+AC=6,求BC的最小值;
例题图②
求两点之间线段最短,可以用哪些知识?
两点之间,垂线段最短,前提是点在直线上
过点B作点C所在直线的垂线
构造直角三角形,勾股定理解题
斜边最短
AB=AC
(2)如解图①,延长BA到点D,使AD=AC,连接DC,过点B作BH⊥CD于点H,
∵∠BAC=120°,∴∠CAD=60°,
∵AD=AC,∴△CAD是等边三角形,
∴BD=AB+AC=6,∠BDC=60°,
∵BH⊥CD,
∴△BDH是直角三角形,
∴在Rt△BDH中,BH=BD·sin∠BDC=3 ,
∵BC≥BH=3 ,
∴当点H与点C重合时,取等号,
∴BC的最小值是3 ;
解图①
问题解决
(3)为了迎接2022年8月6日~11日在榆林举办的陕西省第十七届运动会,某装饰公司在装修运动场馆时,需要设计一块如图③所示的四边形板材ABCD,要求AD∥BC,AB+BC=6米,∠ABC=60°,点P为四边形ABCD内一点,是否存在点P满足∠APC=∠BAD,且点P到四边形板材ABCD的三个顶点A,B,C的距离之和(即PA+PB+PC)最小?若存在,求出PA+PB+PC的最小值;若不存在,请说明理由.
例题图③
特点:同一顶点的线段长,转化到一条线段上
参考(1)中方法,将△BCP顺时针旋转60°,使得PA、PB、PC在一个三角形中
利用边角关系求得三条线段最小值
(3)存在.
如解图②,将△BCP绕着点B顺时针旋转60°后得到△BEF,连接PF,AE,
则EF=CP,△BPF为等边三角形,
∴PF=BP,∴PA+PB+PC=PA+PF+EF≥AE,
∴当A,P,F,E四点共线时,取等号,
∴PA+PB+PC的最小值为AE的长.
延长AB到点G,使BG=BC,连接GE,
由旋转的性质得BE=BC,∠CBE=60°,∴BG=BE,
∵∠ABC=60°,∴∠GBE=60°,
∴△BEG为等边三角形,∴∠BGE=60°,AG=AB+BC=6.
解图②
过点A作AH⊥GE于点H,
∴在Rt△AGH中,AH=AG·sin∠BGE=3 ,
∵AE≥AH=3 ,∴如解图③,当点H与点E重合时,取等号,
∴AE的最小值=3 ,∴PA+PB+PC的最小值=AE的最小值=3 .
∵△BPF是等边三角形,
∴∠BPF=∠BFP=60°,∴∠APB=∠BFE=120°,
由旋转的性质得∠BPC=∠BFE,
∴∠APB=∠BPC=120°,∴∠APC=120°,
∵AD∥BC,∠ABC=60°,∴∠BAD=120°,
∴∠APC=∠BAD.∴存在满足条件的点P,且PA+PB+PC的最小值为3 米.
解图③
练习 (2022陕西预测卷)
问题提出
(1)如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,若延长CD到点E, 使ED=BC,连接AE,得到△ADE≌△ABC,则AC与AE的位置关系是________,数量关系是________;
练习题图
课堂练兵
猜想:位置关系:垂直,数量关系:相等
△ADE≌△ABC
ED=BC
∠EAD=∠CAB
AE=AC
∠BAD=90°
∠BAC=90°
垂直
相等
问题探究
(2)如图②,已知等边△ABC内接于⊙O,P为 上一点,连接AP,BP,CP.若BP=4,求AP+CP的值;
练习题图②
考虑转化到一条线段上
参考(1)中的作法,延长PA,使得AD=PC,连接CB
作辅助线
得全等三角形
依据边角关系求线段和
△ADB≌△CPB
△BPD是等边三角形
DP=AP+AD(PC)=BP
D
解图①
(2)如解图①,延长PA到点D,使AD=CP,连接BD,则△ADB≌△CPB,
∴BD=BP,
∵∠BPD=∠BCA=60°,
∴△BPD是等边三角形,
∴DP=BP=4,
又∵DP=AP+AD=AP+CP,
∴AP+CP=4;
问题解决
(3)有一个直径为80cm的圆形板材⊙O,如图③所示.现需在该板材上裁出一
个四边形ABCD的部件,要求对角线AC平分∠BAD,BD=40 cm,CD=40
cm,并使裁出的四边形ABCD部件的周长最大.试问,是否存在符合要求的周长最大的四边形ABCD部件?若存在,请求出四边形ABCD部件周长的最大值;若不存在,请说明理由.
练习题图③
BC=CD=40cm
BC=CD为定值,
四边形ABCD周长最大
即求AB+AD值最大
作辅助线延长AB到点E,使BE=AD,连接CE
题意可得△ACE∽△DCB
当AC取最大值
AE就有最大值
?
AC为直径取最大
E
(3)存在;
如解图②,延长AB到点E,使BE=AD,连接CE,则△BEC≌△DAC,
∴CE=AC,∠ECB=∠ACD,
∴∠ACE=∠DCB,
又∵∠BAC=∠BDC,
∴△ACE∽△DCB,∴ ,
又∵AC平分∠BAD,∴ ,
∴BC=CD=40cm,即 ,
∴AE= AC,
当AC取最大值时,AE就有最大值.
解图②
解图②
连接OA,OC,
∵AC≤OA+OC=80,∴当点C,O,A共线时,取等号,
∴ACmax=80cm,∴AEmax=80 cm,
又∵AE=AB+BE=AB+AD,∴AB+AD的最大值是80 cm,
∴C四边形ABCD(max)=80( +1)cm,
∴存在符合要求的周长最大的四边形ABCD部件,
其最大值为80( +1)cm.
练习1 (2023陕西预测卷)问题提出
(1)如图①,已知△ABC,试在AB上确定一点P,连接CP,使CP平分S△ABC;
练习1题图①
解:(1)如解图①所示,点P即为所求;
解图①
课后小练
(2)问题探究
如图②,在△ABC中,AD是△ABC的角平分线,求证: ;
练习1题图②
(2)如解图②,过点D分别作DE⊥AC于点E,DF⊥AB
于点F,过点A作AM⊥BC于点M.
∵AD是△ABC的角平分线,∴DE=DF,
∵S△ABD= ×AB·DF= ×BD·AM,
S△ACD= ×AC·DE= ×CD·AM,
∴ ,∴ ;
解图②
(3)问题解决
如图③,某城市想依托原有废旧机车工厂留存的机车铁轨AP改造新的机车主题公园△ABC,点P在BC上,且AP将新的主题公园分为面积相等的两个主题活动区.该项目负责人计划在AB,AC的中点E,F上放置各种年代的机车头作为群众拍照打卡地标,并使得两地标之间距离最大,即EF最大,已知∠BAC=120°,AP=100m.请问是否存在符合要求的△ABC?若存在,请求出EF的最大值;若不存在,请说明理由.
练习题图③
(3)存在.
如解图③,延长AP至点M,使得PM=AP,连接CM,则△CPM≌△BPA,
∴∠ABP=∠MCP,∴AB∥CM,
∵∠BAC=120°,∴∠ACM=60°,
∴点C在以AM为弦,其所对圆周角为60°的圆弧上运动,圆弧的圆心为点O,
∵点E,F分别是AB,AC的中点,
∴EF是△ABC的中位线,∴EF= BC,
∴BC最大时,EF最大,
∵点P为BC的中点,
∴BC=2CP,即CP最大时,BC最大,
解图③
解图③
∴PC最大时,EF最大,EF= BC= ×2PC=PC,
当C,O,P三点共线,即点C位于点C′处时,PC最大,即为PC′,此时△AC′M为等边三角形,
∴PC′=AP·tan60°=100 ,
∴PC的最大值为100 ,∴EF的最大值为100 m.
练习2 (2022陕西黑白卷)问题提出
(1)如图①,在Rt△ABC中,∠ABC=90°,AB=3,BC=6,求Rt△ABC外接圆的半径;
练习2题图①
解:(1)∵∠ABC=90°,AB=3,
BC=6,
∴AC= ,
∴Rt△ABC外接圆的半径为 AC= ;
问题解决
(2)如图②,某园林规划局计划在一片空地上开垦出一片区域ABCD,用于种植珍稀树苗,且用栅栏保护.其中四边形ABCD为平行四边形,连接AC,BM平分∠ABC交AC于点M,BM=40 m,∠ABC=60°.为了尽可能地减少栅栏地使用,需使四边形ABCD的周长最小,你认为该园林规划局的想法能否实现?若能,请求出四边形ABCD周长的最小值;若不能,请说明理由.
练习2题图②
(2)能实现.
如解图①,过点M作ME⊥AB于点E,MF⊥BC于点F,
∵∠ABC=60°,BM平分∠ABC,
∴∠EBM=∠FBM=30°,∴△BEM≌△BFM,
∴BE=BF= BM=20 ,ME=MF= BM=20.
∵四边形ABCD是平行四边形,
∴C ABCD=2(AB+BC)=2(BE+AE+BF+CF).
∵BE=BF=20 ,
∴要使得四边形ABCD的周长最小,即AE+CF最小.
解图①
∵在四边形EBFM中,∠EBF=60°,
∴∠EMF=120°,∴∠AME+∠FMC=60°.
将△AME绕点M逆时针旋转,使得ME与MF重合,得到△A′MF,
由旋转的性质可得,EA=A′F,∠AME=∠A′MF,
∴∠A′MF+∠FMC=60°.
∵∠AEM=∠CFM=90°,∴∠A′FM+∠CFM=180°.
∴A′,F,C三点共线,
∴AE+CF=A′F+CF=A′C,
∴AE+CF的最小值即为A′C的最小值.
在△MA′C中,∠A′MC=60°,MF=20.
解图①
如解图②,作△MA′C的外接圆⊙G,连接GM,GA′,GC,过点G作GH⊥A′C于点H,
∴∠A′GC=2∠A′MC=120°.
∵A′G=CG,∴∠GA′C=∠GCA′=30°,
∴GH= A′G= GM,A′C=2× A′G= GM.
∵GM+GH≥MF,∴GM+ GM≥MF,
即 GM≥20,∴GM≥ ,
∴A′C= GM≥ ,∴A′C的最小值为 ,
∴C ABCD=2(BE+AE+BF+CF)≥2×(20 +20 + )= m.
即四边形ABCD周长的最小值为 m.
解图②
同课章节目录
