9.5三角形的中位线 苏科版初中数学八年级下册同步练习(含解析)
文档属性
| 名称 | 9.5三角形的中位线 苏科版初中数学八年级下册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 474.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.5三角形的中位线苏科版初中数学八年级下册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,在中,,分别是,的中点,,是上一点,连接,,若,则的长度为
( )
A.
B.
C.
D.
2.如图,将矩形绕点顺时针旋转得到矩形,点、分别是、的中点,若,,则的长
( )
A.
B.
C.
D.
3.如图,在四边形中,,,,分别是,,的中点.若,,则等于( )
A. B. C. D.
4.如图,在中,平分,于点,点是的中点,若,,则的长为
( )
A.
B.
C.
D.
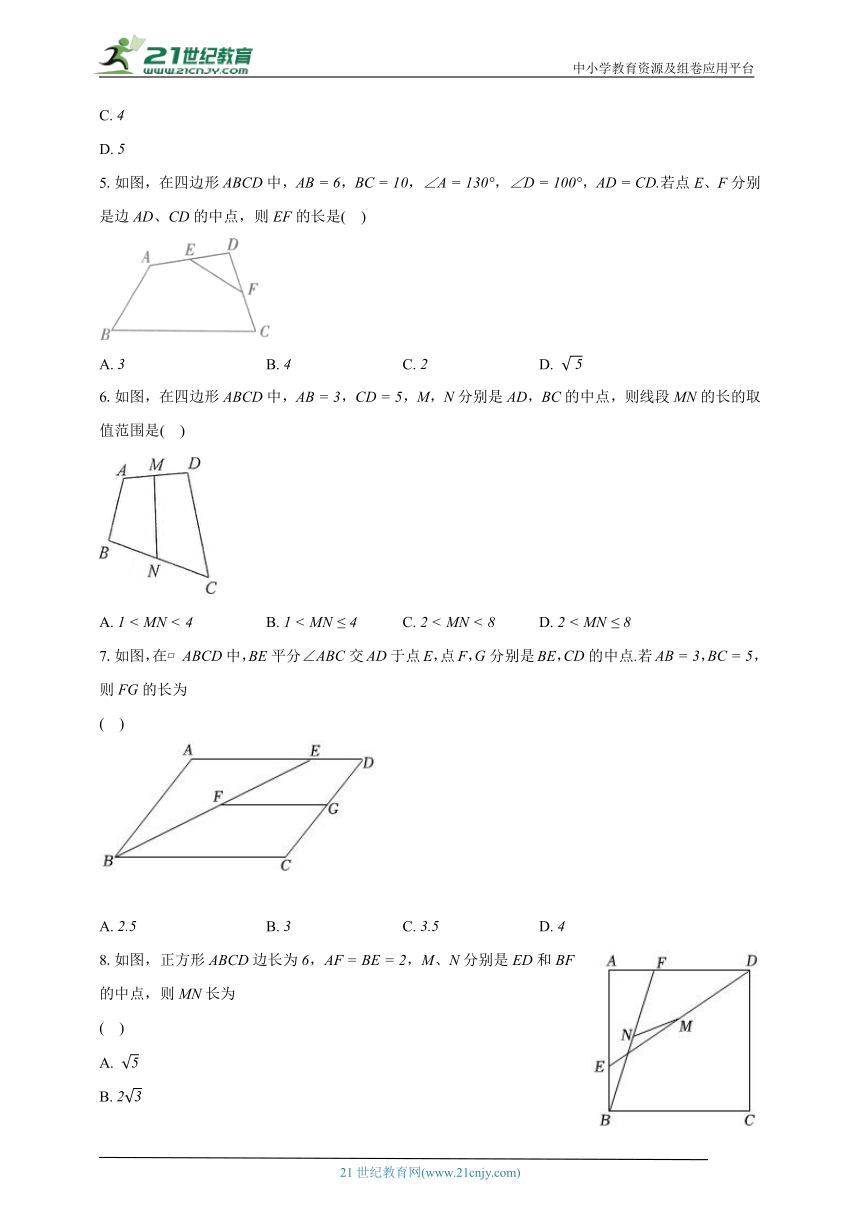
5.如图,在四边形中,,,,,若点、分别是边、的中点,则的长是( )
A. B. C. D.
6.如图,在四边形中,,,,分别是,的中点,则线段的长的取值范围是( )
A. B. C. D.
7.如图,在 中,平分交于点,点,分别是,的中点若,,则的长为
( )
A. B. C. D.
8.如图,正方形边长为,,、分别是和的中点,则长为
( )
A.
B.
C.
D.
9.如图,的对角线、相交于点,的平分线与边相交于点,是的中点.若,,则的长为
( )
A. B. C. D.
10.如图, 的周长为,对角线、相交于点,点是的中点,,则的周长为( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,在矩形中,是边上一点,、分别是、的中点,连接、、若,,,则矩形的面积为 .
12.如图,在矩形纸片中,,,为边上一点.将沿所在的直线折叠,点恰好落在边上的点处,过点作,垂足为,取的中点,连接,则 .
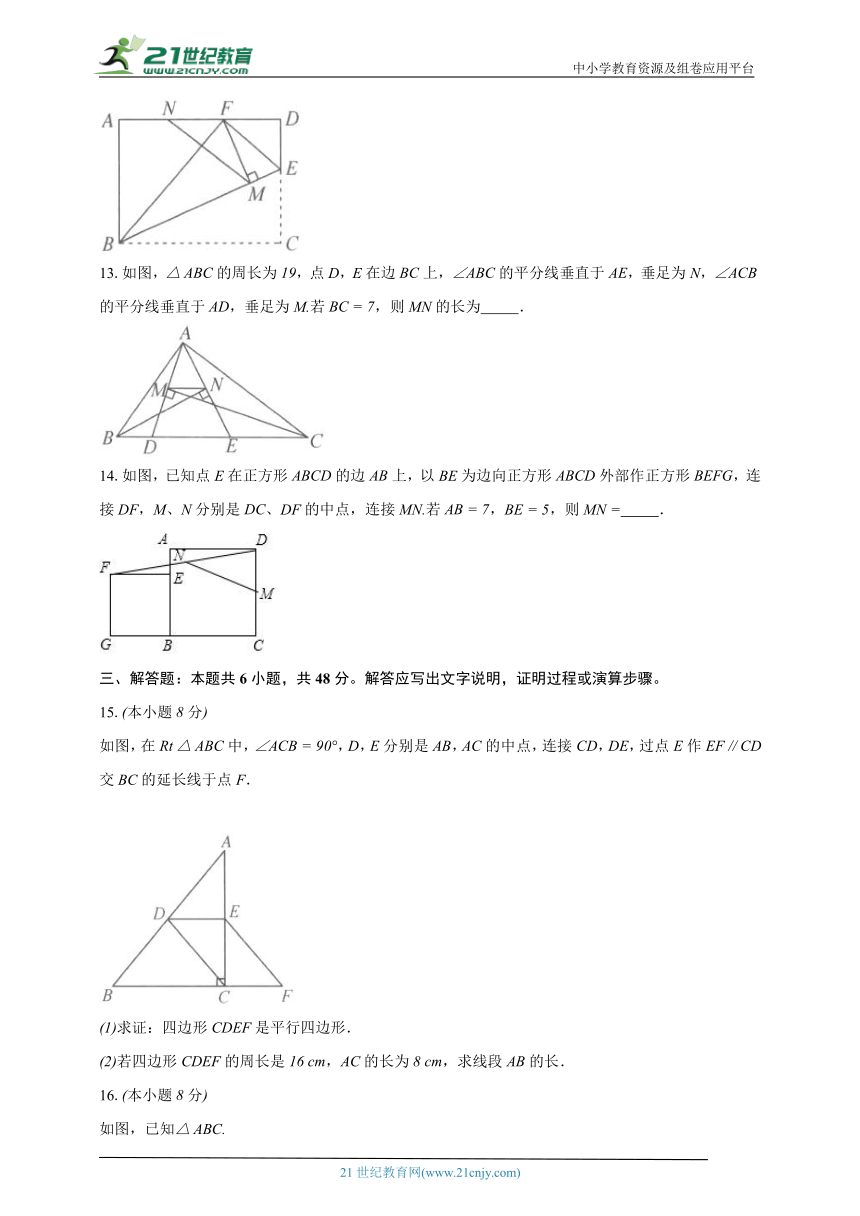
13.如图,的周长为,点,在边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为若,则的长为 .
14.如图,已知点在正方形的边上,以为边向正方形外部作正方形,连接,、分别是、的中点,连接若,,则 .
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在中,,,分别是,的中点,连接,,过点作交的延长线于点.
求证:四边形是平行四边形.
若四边形的周长是,的长为,求线段的长.
16.本小题分
如图,已知
用尺规作图作中点,中点,并连接保留作图痕迹
我们知道,三角形的中位线平行于第三条边,并且等于第三条边的一般,请证明中位线定理.
17.本小题分
如图,中,、分别为边、中点,连接并延长至点,使得,连接
求证:≌;
若,,求四边形的周长.
18.本小题分
如图,在四边形中,、分别是、的中点,、分别是、的中点,,与有什么位置关系?请说明理由.
19.本小题分
如图,等边的边长是,、分别为、的中点,延长至点,使,连接和.
求证:;
求的长.
20.本小题分
如图,在四边形中,,,、分别为、的中点,连接、、.
求证:;
若,平分,,求的长.
答案和解析
1.【答案】
【解析】如图,首先证明,继而得到;证明为的中位线,即可解决问题.
该题主要考查了三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题;牢固掌握三角形的中位线定理、直角三角形的性质等几何知识点是解题的基础和关键.
解:如图,,,
,;
,分别是,的中点,
为的中位线,
,
故选:
2.【答案】
【解析】解:连接、、,如图所示:
矩形绕点顺时针旋转得到矩形,
,
,与互相平分,与互相平分,
点、分别是、的中点,
是的中点,是的中点,
是的中位线,
,
,
是等腰直角三角形,
,
故选:
连接、、,由矩形的性质和勾股定理求出,由矩形的性质得出是的中点,是的中点,证出是的中位线,由三角形中位线定理得出,由等腰直角三角形的性质得出,即可得出结果.
本题考查了矩形的性质、旋转的性质、勾股定理、等腰直角三角形的判定与性质、三角形中位线定理;熟练掌握矩形的性质,由三角形中位线定理求出是解决问题的关键.
3.【答案】
【解析】由条件,得,,,所以,,所以,所以.
4.【答案】
【解析】解:延长,交于点,
平分,,
,,
,,
,
,
点是的中点,,
为中位线,
故选:
根据角平分线的性质构造辅助线,再根据三角形中位线定理解答即可.
本题考查的是三角形中位线定理、等腰三角形的性质与判定,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】解:如图,连接,交于点,
四边形是平行四边形,
,,
,
平分,
,
,
,
,
点,分别是和的中点,且,
是的中位线,是的中位线,
,
,
故选
根据平行四边形的性质得出,进而利用平行线的性质和三角形的中位线定理解答即可.
此题考查平行四边形的性质,三角形的中位线定理,关键是掌握平行四边形的性质.
8.【答案】
【解析】解:延长交的延长线于点,连接,
四边形是正方形,
,
,
是的中点,
,
在和中,
≌,
,,
即点是的中点,
是的中点,
是的中位线,
,
四边形是正方形,
,,
,
,
,
在中,由勾股定理得,
,
故选:
延长交的延长线于点,连接,根据正方形的性质和已知条件可证得和全等,从而得出是的中位线,在中根据勾股定理求出的长,然后根据三角形中位线定理即可求出的长.
本题考查了正方形的性质,三角形全等的判定与性质,三角形中位线定理,正确添加辅助线是解题的关键.
9.【答案】
【解析】略
10.【答案】
【解析】解:平行四边形的周长为,
,
,,
,
,
,
的周长为,
故选:.
利用平行四边形的性质,三角形中位线定理即可解决问题.
本题考查平行四边形的性质、三角形的中位线定理等知识,解题的关键是熟练掌握三角形中位线定理,属于中考常考题型.
11.【答案】
【解析】略
12.【答案】
【解析】连接,,由折叠的性质可知,垂直平分线段,所以因为,所以,,三点共线,所以因为四边形是矩形,所以,所以因为是的中点,是的中点,所以是的中位线,所以.
13.【答案】
【解析】因为平分,,所以,所以≌,所以,,所以是等腰三角形.同理可得,是等腰三角形.所以是的中位线,所以因为,所以所以.
14.【答案】
【解析】【分析】
本题考查了正方形的性质及三角形中位线定理、勾股定理的运用.构造基本图形是解题的关键.
连接,则为的中位线,根据勾股定理求出长即可求出的长.
【解答】
解:连接,
正方形和正方形中,,,
,,,
,
在中,.
、分别是、的中点,
.
故答案为:.
15.【答案】【小题】
证明:因为,分别是,的中点,所以是的中位线,所以又因为,所以四边形是平行四边形.
【小题】
解:因为四边形是平行四边形,所以因为是斜边上的中线,所以由,得,所以四边形的周长等于长与长的和.设,则在中,因为,所以,即,解得所以线段的长为.
【解析】 见答案
见答案
16.【答案】【小题】
解:如图,为所作;
【小题】
解:已知:为的中位线,如图,
求证:,
证明:延长到点使,如图,
为的中点,
,,
在和中,
≌,
,,
,,
四边形为平行四边形,
,,
而,
,
【解析】
分别作和的垂直平分线得到的中点,的中点;
先写出已知、求证,延长到点使,如图,先证明≌得到,,再证明四边形为平行四边形得到,,于是有,
本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质和三角形中位线定理.
17.【答案】【小题】
证明:点是的中点,
,
又,,
≌,
【小题】
、分别为边、中点,
,,
,
四边形是平行四边形,
,点是中点,
,
四边形的周长
【解析】
由“”可证≌;
由三角形中位线定理可得,,可证四边形是平行四边形,由平行四边形的性质可求解.
本题考查了全等三角形的判定和性质,三角形中位线定理,平行四边形的判定和性质等知识,灵活运用这些性质进行推理是本题的关键.
18.【答案】与互相垂直.理由:连接、、、.
、分别是、的中点,,
同理,,.
又,,
四边形是菱形,与互相垂直.
【解析】见答案
19.【答案】【小题】
、分别为、的中点,为的中位线,,,.
【小题】
由可知,,,四边形为平行四边形,在等边中,为中点,,,,.
【解析】 见答案
见答案
20.【答案】【小题】
在中,、分别是、的中点,
,在中,是中点,,,.
【小题】
,平分,由可知,,,,,由可知,.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.5三角形的中位线苏科版初中数学八年级下册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,在中,,分别是,的中点,,是上一点,连接,,若,则的长度为
( )
A.
B.
C.
D.
2.如图,将矩形绕点顺时针旋转得到矩形,点、分别是、的中点,若,,则的长
( )
A.
B.
C.
D.
3.如图,在四边形中,,,,分别是,,的中点.若,,则等于( )
A. B. C. D.
4.如图,在中,平分,于点,点是的中点,若,,则的长为
( )
A.
B.
C.
D.
5.如图,在四边形中,,,,,若点、分别是边、的中点,则的长是( )
A. B. C. D.
6.如图,在四边形中,,,,分别是,的中点,则线段的长的取值范围是( )
A. B. C. D.
7.如图,在 中,平分交于点,点,分别是,的中点若,,则的长为
( )
A. B. C. D.
8.如图,正方形边长为,,、分别是和的中点,则长为
( )
A.
B.
C.
D.
9.如图,的对角线、相交于点,的平分线与边相交于点,是的中点.若,,则的长为
( )
A. B. C. D.
10.如图, 的周长为,对角线、相交于点,点是的中点,,则的周长为( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,在矩形中,是边上一点,、分别是、的中点,连接、、若,,,则矩形的面积为 .
12.如图,在矩形纸片中,,,为边上一点.将沿所在的直线折叠,点恰好落在边上的点处,过点作,垂足为,取的中点,连接,则 .
13.如图,的周长为,点,在边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为若,则的长为 .
14.如图,已知点在正方形的边上,以为边向正方形外部作正方形,连接,、分别是、的中点,连接若,,则 .
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在中,,,分别是,的中点,连接,,过点作交的延长线于点.
求证:四边形是平行四边形.
若四边形的周长是,的长为,求线段的长.
16.本小题分
如图,已知
用尺规作图作中点,中点,并连接保留作图痕迹
我们知道,三角形的中位线平行于第三条边,并且等于第三条边的一般,请证明中位线定理.
17.本小题分
如图,中,、分别为边、中点,连接并延长至点,使得,连接
求证:≌;
若,,求四边形的周长.
18.本小题分
如图,在四边形中,、分别是、的中点,、分别是、的中点,,与有什么位置关系?请说明理由.
19.本小题分
如图,等边的边长是,、分别为、的中点,延长至点,使,连接和.
求证:;
求的长.
20.本小题分
如图,在四边形中,,,、分别为、的中点,连接、、.
求证:;
若,平分,,求的长.
答案和解析
1.【答案】
【解析】如图,首先证明,继而得到;证明为的中位线,即可解决问题.
该题主要考查了三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题;牢固掌握三角形的中位线定理、直角三角形的性质等几何知识点是解题的基础和关键.
解:如图,,,
,;
,分别是,的中点,
为的中位线,
,
故选:
2.【答案】
【解析】解:连接、、,如图所示:
矩形绕点顺时针旋转得到矩形,
,
,与互相平分,与互相平分,
点、分别是、的中点,
是的中点,是的中点,
是的中位线,
,
,
是等腰直角三角形,
,
故选:
连接、、,由矩形的性质和勾股定理求出,由矩形的性质得出是的中点,是的中点,证出是的中位线,由三角形中位线定理得出,由等腰直角三角形的性质得出,即可得出结果.
本题考查了矩形的性质、旋转的性质、勾股定理、等腰直角三角形的判定与性质、三角形中位线定理;熟练掌握矩形的性质,由三角形中位线定理求出是解决问题的关键.
3.【答案】
【解析】由条件,得,,,所以,,所以,所以.
4.【答案】
【解析】解:延长,交于点,
平分,,
,,
,,
,
,
点是的中点,,
为中位线,
故选:
根据角平分线的性质构造辅助线,再根据三角形中位线定理解答即可.
本题考查的是三角形中位线定理、等腰三角形的性质与判定,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】解:如图,连接,交于点,
四边形是平行四边形,
,,
,
平分,
,
,
,
,
点,分别是和的中点,且,
是的中位线,是的中位线,
,
,
故选
根据平行四边形的性质得出,进而利用平行线的性质和三角形的中位线定理解答即可.
此题考查平行四边形的性质,三角形的中位线定理,关键是掌握平行四边形的性质.
8.【答案】
【解析】解:延长交的延长线于点,连接,
四边形是正方形,
,
,
是的中点,
,
在和中,
≌,
,,
即点是的中点,
是的中点,
是的中位线,
,
四边形是正方形,
,,
,
,
,
在中,由勾股定理得,
,
故选:
延长交的延长线于点,连接,根据正方形的性质和已知条件可证得和全等,从而得出是的中位线,在中根据勾股定理求出的长,然后根据三角形中位线定理即可求出的长.
本题考查了正方形的性质,三角形全等的判定与性质,三角形中位线定理,正确添加辅助线是解题的关键.
9.【答案】
【解析】略
10.【答案】
【解析】解:平行四边形的周长为,
,
,,
,
,
,
的周长为,
故选:.
利用平行四边形的性质,三角形中位线定理即可解决问题.
本题考查平行四边形的性质、三角形的中位线定理等知识,解题的关键是熟练掌握三角形中位线定理,属于中考常考题型.
11.【答案】
【解析】略
12.【答案】
【解析】连接,,由折叠的性质可知,垂直平分线段,所以因为,所以,,三点共线,所以因为四边形是矩形,所以,所以因为是的中点,是的中点,所以是的中位线,所以.
13.【答案】
【解析】因为平分,,所以,所以≌,所以,,所以是等腰三角形.同理可得,是等腰三角形.所以是的中位线,所以因为,所以所以.
14.【答案】
【解析】【分析】
本题考查了正方形的性质及三角形中位线定理、勾股定理的运用.构造基本图形是解题的关键.
连接,则为的中位线,根据勾股定理求出长即可求出的长.
【解答】
解:连接,
正方形和正方形中,,,
,,,
,
在中,.
、分别是、的中点,
.
故答案为:.
15.【答案】【小题】
证明:因为,分别是,的中点,所以是的中位线,所以又因为,所以四边形是平行四边形.
【小题】
解:因为四边形是平行四边形,所以因为是斜边上的中线,所以由,得,所以四边形的周长等于长与长的和.设,则在中,因为,所以,即,解得所以线段的长为.
【解析】 见答案
见答案
16.【答案】【小题】
解:如图,为所作;
【小题】
解:已知:为的中位线,如图,
求证:,
证明:延长到点使,如图,
为的中点,
,,
在和中,
≌,
,,
,,
四边形为平行四边形,
,,
而,
,
【解析】
分别作和的垂直平分线得到的中点,的中点;
先写出已知、求证,延长到点使,如图,先证明≌得到,,再证明四边形为平行四边形得到,,于是有,
本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质和三角形中位线定理.
17.【答案】【小题】
证明:点是的中点,
,
又,,
≌,
【小题】
、分别为边、中点,
,,
,
四边形是平行四边形,
,点是中点,
,
四边形的周长
【解析】
由“”可证≌;
由三角形中位线定理可得,,可证四边形是平行四边形,由平行四边形的性质可求解.
本题考查了全等三角形的判定和性质,三角形中位线定理,平行四边形的判定和性质等知识,灵活运用这些性质进行推理是本题的关键.
18.【答案】与互相垂直.理由:连接、、、.
、分别是、的中点,,
同理,,.
又,,
四边形是菱形,与互相垂直.
【解析】见答案
19.【答案】【小题】
、分别为、的中点,为的中位线,,,.
【小题】
由可知,,,四边形为平行四边形,在等边中,为中点,,,,.
【解析】 见答案
见答案
20.【答案】【小题】
在中,、分别是、的中点,
,在中,是中点,,,.
【小题】
,平分,由可知,,,,,由可知,.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
