11.3用反比例函数解决问题 苏科版初中数学八年级下册同步练习(含解析)
文档属性
| 名称 | 11.3用反比例函数解决问题 苏科版初中数学八年级下册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 484.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 12:20:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.3用反比例函数解决问题苏科版初中数学八年级下册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某药品研究所开发了一种新药,经大量动物实验,首次用于临床人体实验,测得成人服药后血液中的药物浓度与服药时间之间的函数关系如图所示当时,与成反比若血液中的药物浓度不低于的持续时间不低于,则称药物治疗有效.根据图像信息计算并判断下列选项错误的是( )
A. 当血液中的药物浓度上升时,与之间的函数表达式为
B. 当血液中的药物浓度下降时,与之间的函数表达式为
C. 血液中的药物浓度不低于的持续时间为
D. 这种抗菌新药不可以作为有效药物投入生产
2.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自年月开始限产进行治污改造,其月利润万元与月份之间的变化如图所示,治污完成前是反比例函数图像的一部分,治污完成后是一次函数图像的一部分,下列选项错误的是( )
A. 月份的利润为万元
B. 治污改造完成后每月利润比前一个月增加万元
C. 治污改造完成前后共有个月的利润低于万元
D. 月份该厂的利润达到万元
3.某市举行中学生党史知识竞赛.如图,用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率该校优秀人数与该校参加竞赛人数的百分比与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中优秀人数最多的是( )
A. 甲 B. 乙 C. 丙 D. 丁
4.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物的措施进行消毒在对某宿舍进行消毒的过程中,先经过的集中药物喷洒,再封闭宿舍,然后打开门窗进行通风室内空气中含药量与药物在空气中的持续时间之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又满足反比例函数,图像如图所示下列选项中,错误的是
( )
A. 经过的集中药物喷洒,室内空气中的含药量最高达到
B. 室内空气中的含药量不低于的持续时间达到了
C. 若室内空气中的含药量不低于且持续时间不低于,才能有效杀灭某种传染病毒,则此次消毒完全有效
D. 当室内空气中的含药量低于时,对人体才是安全的,因此从室内空气中的含药量达到开始,至少需经过,学生才能进入室内
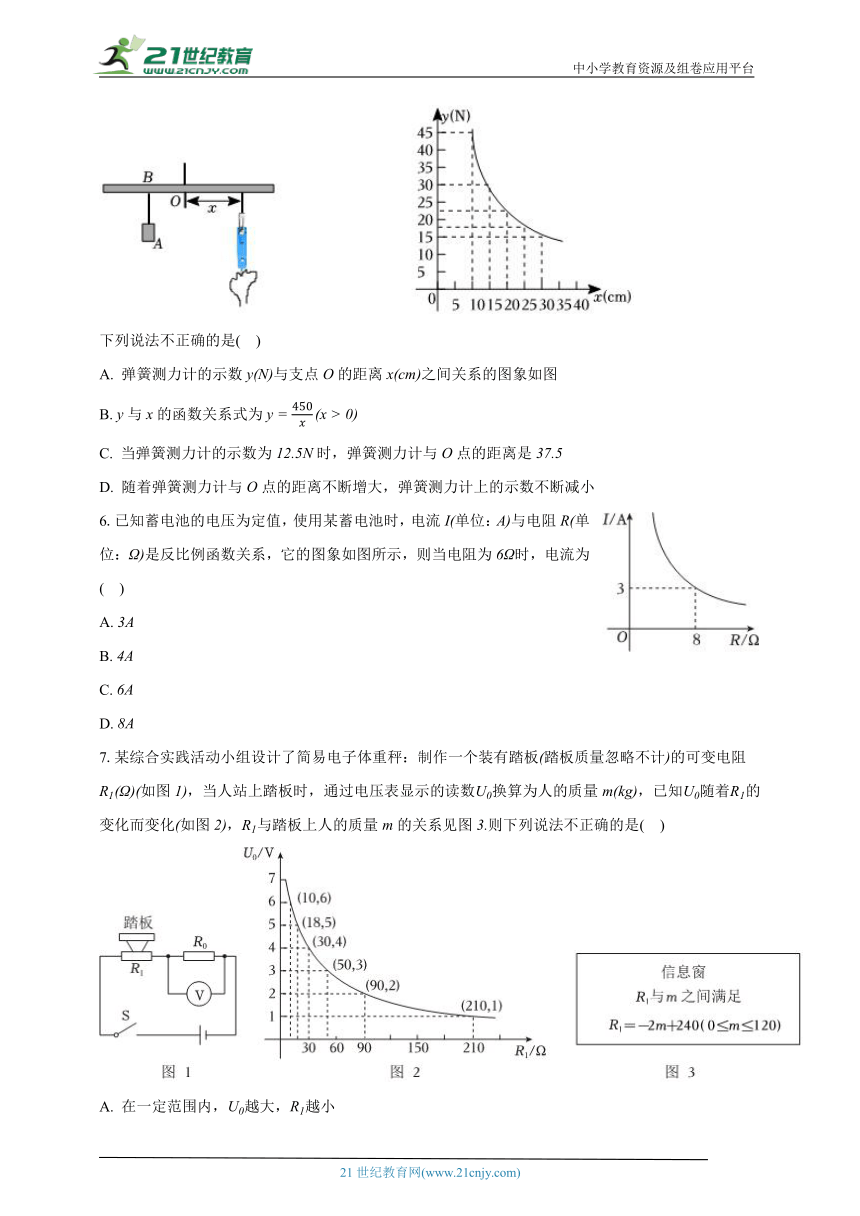
5.如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点左侧固定位置处悬挂重物,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点的距离,观察弹簧测力计的示数的变化情况实验数据记录如下表:
下列说法不正确的是( )
A. 弹簧测力计的示数与支点的距离之间关系的图象如图
B. 与的函数关系式为
C. 当弹簧测力计的示数为时,弹簧测力计与点的距离是
D. 随着弹簧测力计与点的距离不断增大,弹簧测力计上的示数不断减小
6.已知蓄电池的电压为定值,使用某蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A.
B.
C.
D.
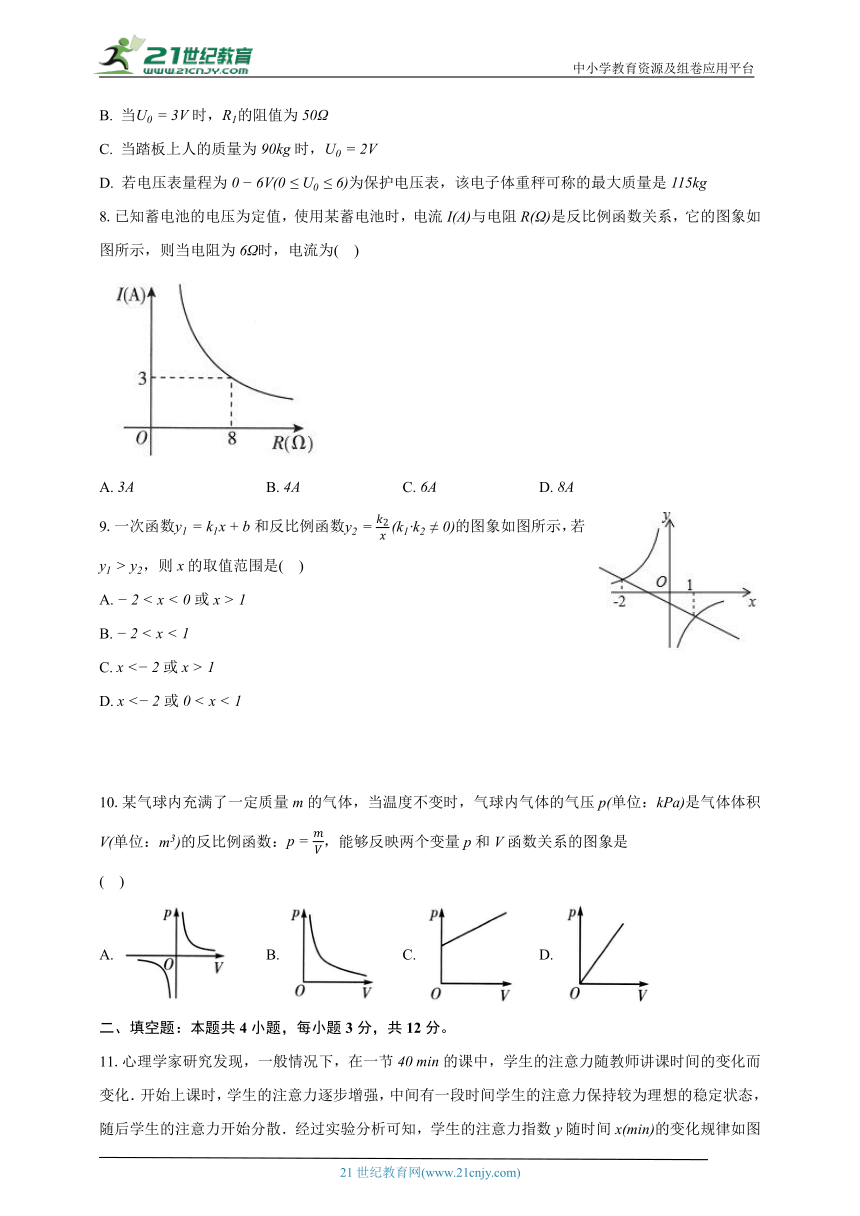
7.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板踏板质量忽略不计的可变电阻如图,当人站上踏板时,通过电压表显示的读数换算为人的质量,已知随着的变化而变化如图,与踏板上人的质量的关系见图则下列说法不正确的是( )
A. 在一定范围内,越大,越小
B. 当时,的阻值为
C. 当踏板上人的质量为时,
D. 若电压表量程为为保护电压表,该电子体重秤可称的最大质量是
8.已知蓄电池的电压为定值,使用某蓄电池时,电流与电阻是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A. B. C. D.
9.一次函数和反比例函数的图象如图所示,若,则的取值范围是( )
A. 或
B.
C. 或
D. 或
10.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压单位:是气体体积单位:的反比例函数:,能够反映两个变量和函数关系的图象是
( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
11.心理学家研究发现,一般情况下,在一节的课中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数随时间的变化规律如图所示,其中,分别为线段,为双曲线的一部分.上课开始时,注意力指数为,第时,注意力指数为根据图像信息,若开始上课第学生的注意力指数与下课时的注意力指数相等,则的值为 .
12.由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值始终保持,发现通过滑动变阻器的电流与滑动变阻器的电阻成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过,则滑动变阻器阻值的范围是 .
13.某气球内充满了一定质量的气体,当温度不变的条件下,气球内气体的气压是气球体积的反比例函数,且当时,当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .
14.你吃过拉面吗实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度是面条的粗细横截面积的反比例函数,其图像如图所示,则当面条粗时,面条的总长度是
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
某校对教室采取喷洒药物的方式进行消毒,在消毒过程中,先进行的药物喷洒,接着封闭教室,然后打开门窗进行通风.教室内每立方米空气中的含药量与药物在空气中的持续时间之间的函数关系如图所示,在打开门窗通风前分别满足两个一次函数关系,在通风后满足反比例函数关系.
求药物喷洒后空气中的含药量与药物在空气中的持续时间之间的函数表达式.
如果室内空气中的含药量不低于且持续时间不低于才能有效消毒,请通过计算说明此次消毒是否有效.
16.本小题分
已知某品牌运动鞋每双进价元,为求合适的销售价格进行了天的试销,试销情况如下表:
试销天数 第天 第天 第天 第天
售价元双
销售量双
表中数据,满足什么函数表达式?请求出这个函数表达式.
若每天的销售利润为元,则单价应定为多少?
17.本小题分
某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚里温度随时间时变化的函数图像,其中段是恒温阶段,段是双曲线的一部分.请根据图中信息解答下列问题:
求的值.
求恒温系统在一天内保持大棚里温度在及以上的时长.
18.本小题分
实验数据显示,一般成人喝毫升某品牌白酒后,血液中酒精含量毫克百毫升关于时间时变化的图像如图所示图像由线段与部分双曲线组成国家规定,车辆驾驶人员血液中的酒精含量大于或等于毫克百毫升时属于“酒后驾驶”,不能驾车上路.
求部分双曲线的函数表达式;
参照上述数学模型,假设某驾驶员晚上在家喝完毫升该品牌白酒,第二天早上能否驾车去上班?请说明理由.
19.本小题分
方方驾驶小汽车从地匀速行驶到地,行驶里程为千米,设小汽车的行驶时间为时,行驶速度为千米时,且全程速度限定为不超过千米时.
求关于的函数表达式;
方方上午点驾驶小汽车从地出发.
方方需在当天点分至点含点分和点间到达地,求小汽车行驶速度的范围;
方方能否在当天点分前到达地?说明理由.
20.本小题分
某蓄水池员工对一蓄水池进行排水,该蓄水池每小时的排水量与排完水池中的水所用的时间之间的函数关系图像如图所示.
该蓄水池的蓄水量为 ;
如果每小时排水量不超过,那么排完水池中的水所用的时间满足的条件是 .
由于该蓄水池员工有其他任务,为了提前排完水池中的水,需将原计划每小时的排水量增加,求原计划每小时的排水量是多少立方米?
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】略
3.【答案】
【解析】【分析】
本题考查了反比例函数的图象上点的坐标特征,结合实际含义理解图象上点的坐标含义是解题的关键.
根据题意可知的值即为该校的优秀人数,再根据图象即可确定丙校的优秀人数最多.
【解答】
解:根据题意,可知的值即为该校的优秀人数,
描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,
乙、丁两所学校的优秀人数相同,
点丙在反比例函数图象上面,
丙校的的值最大,即优秀人数最多,
故选:.
4.【答案】
【解析】【分析】
本题考查反比例函数的应用、一次函数的应用等知识,解题的关键是读懂图象信息,属于中考常考题型.
利用图中信息一一判断即可
解:、正确不符合题意.
B、由题意时,,室内空气中的含药量不低于的持续时间达到了,正确,不符合题意
C、时,或,,故本选项错误,符合题意
D、当时,函数关系式为,时,当时,函数关系式为,时,,故
当室内空气中的含药量低于时,对人体才是安全的,所以从室内空气中的含药量达到开始,需经过后,学
生才能进入室内,正确不符合题意,
故选:.
5.【答案】
【解析】解:由图象猜测与之间的函数关系为反比例函数.
所以设,
把,代入求得,
,
将其余各点代入验证均适合,
与的函数关系式为,
把代入,得,
当弹簧测力计的示数为时,弹簧测力计与点的距离是,
随着弹簧测力计与点的距离不断增大,弹簧测力计上的示数不断减小.
故选:.
仔细观察表格,在坐标系中分别描出各点,并平滑曲线连接这些点,即可画出函数图象;观察所画图形,回想常见几种函数的图象特征,即可判断出函数类型,利用待定系数法求出函数关系式;把代入上面所得关系式求解,并根据函数的性质判断弹簧秤与点的距离不断增大时的弹簧测力计示数变化情况.
此题考查的是反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
6.【答案】
【解析】解:设,
图象过,
,
,
当电阻为时,电流为:.
故选:.
根据函数图象可设,再将代入即可得出函数关系式,从而解决问题.
本题考查了反比例函数的应用,关键是掌握函数图象上点的坐标必能满足解析式.
7.【答案】
【解析】解:图中随的增大而减小,
在一定范围内,越大,越小.
A正确,不符合题意;
图中的图象经过点,
当时,的阻值为.
B正确,不符合题意;
当时,,时,对应的是,
踏板上人的质量为时,,错误.
符合题意.
,
随的增大而减小.
的最小值为,
的最大值为.
若电压表量程为为保护电压表,该电子体重秤可称的最大质量是.
D正确,不符合题意.
故选:.
根据图中随的增大而减小可得选项正确;图中的图象经过点,可得选项B正确;把代入图三可得为,而时,对应的是,故C错误;根据图三可得随的增大而减小,所用求的最大值,找到的最小值代入即可求得最大该电子体重秤可称的最大质量.
本题综合考查一次函数与反比例函数的应用.结合题意,理解两种函数表达式的意义及性质是解决本题的关键.
8.【答案】
【解析】略
9.【答案】
【解析】解:根据函数图象可知,当或时,一次函数图象在反比例函数图象的上方,
当时,的取值范围是:或.
故选:.
当一次函数的值大于反比例函数的值时,直线在双曲线的上方,根据图象可得出当时,的取值范围.
此题主要考查了反比例函数与一次函数的交点问题,正确利用函数图象分析是解题关键.
10.【答案】
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】略
13.【答案】略
【解析】略
14.【答案】
【解析】略
15.【答案】【小题】
解:当时,设,将点代入,得,解得,所以;当时,设,将点,代入,得解得所以;当时,设,将点代入,得,所以所以所求函数表达式为
【小题】
令,解得;令,解得因为,所以此次消毒有效.
【解析】 见答案
见答案
16.【答案】【小题】
解:由题表中数据,得,所以是的反比例函数,这个函数表达式为.
【小题】
根据题意,得,解得经检验,是原方程的根,所以单价应定为元双.
答:若每天的销售利润为元,则其单价应定为元双.
【解析】 见答案
见答案
17.【答案】【小题】
解:将点代入,得.
【小题】
设开启段的函数表达式为将点,代入,得解得所以开启段的函数表达式为将代入,得将代入,得所以.
答:恒温系统在一天内保持大棚里温度在及以上的时长为.
【解析】 见答案
见答案
18.【答案】【小题】
解:依题意,直线过,则直线的函数表达式为,
当时,,即,
设双曲线的函数表达式为,将点代入,得,
部分双曲线的函数表达式为
【小题】
不能.理由如下:
由,得当时,,
从晚上到第二天早上时间间距为小时,
,驾驶员第二天早上不能驾车去上班.
【解析】 见答案
见答案
19.【答案】【小题】
解:,且全程速度限定为不超过千米时,
关于的函数表达式为.
【小题】
点至点分时长为小时,点至点时长为小时,,将代入,得;将代入,得.
小汽车行驶速度的范围为千米时千米时.
方方不能在当天点分前到达地.理由如下:
点至点分时长为小时,.
故方方不能在当天点分前到达地.
【解析】 见答案
见答案
20.【答案】【小题】
【小题】
【小题】
解:设原计划每小时的排水量为,则实际每小时的排水量为,根据题意,得,
解得经检验,是原方程的解,且符合题意.
答:原计划每小时的排水量是.
【解析】 见答案
见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.3用反比例函数解决问题苏科版初中数学八年级下册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某药品研究所开发了一种新药,经大量动物实验,首次用于临床人体实验,测得成人服药后血液中的药物浓度与服药时间之间的函数关系如图所示当时,与成反比若血液中的药物浓度不低于的持续时间不低于,则称药物治疗有效.根据图像信息计算并判断下列选项错误的是( )
A. 当血液中的药物浓度上升时,与之间的函数表达式为
B. 当血液中的药物浓度下降时,与之间的函数表达式为
C. 血液中的药物浓度不低于的持续时间为
D. 这种抗菌新药不可以作为有效药物投入生产
2.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自年月开始限产进行治污改造,其月利润万元与月份之间的变化如图所示,治污完成前是反比例函数图像的一部分,治污完成后是一次函数图像的一部分,下列选项错误的是( )
A. 月份的利润为万元
B. 治污改造完成后每月利润比前一个月增加万元
C. 治污改造完成前后共有个月的利润低于万元
D. 月份该厂的利润达到万元
3.某市举行中学生党史知识竞赛.如图,用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率该校优秀人数与该校参加竞赛人数的百分比与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中优秀人数最多的是( )
A. 甲 B. 乙 C. 丙 D. 丁
4.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物的措施进行消毒在对某宿舍进行消毒的过程中,先经过的集中药物喷洒,再封闭宿舍,然后打开门窗进行通风室内空气中含药量与药物在空气中的持续时间之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又满足反比例函数,图像如图所示下列选项中,错误的是
( )
A. 经过的集中药物喷洒,室内空气中的含药量最高达到
B. 室内空气中的含药量不低于的持续时间达到了
C. 若室内空气中的含药量不低于且持续时间不低于,才能有效杀灭某种传染病毒,则此次消毒完全有效
D. 当室内空气中的含药量低于时,对人体才是安全的,因此从室内空气中的含药量达到开始,至少需经过,学生才能进入室内
5.如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点左侧固定位置处悬挂重物,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点的距离,观察弹簧测力计的示数的变化情况实验数据记录如下表:
下列说法不正确的是( )
A. 弹簧测力计的示数与支点的距离之间关系的图象如图
B. 与的函数关系式为
C. 当弹簧测力计的示数为时,弹簧测力计与点的距离是
D. 随着弹簧测力计与点的距离不断增大,弹簧测力计上的示数不断减小
6.已知蓄电池的电压为定值,使用某蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A.
B.
C.
D.
7.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板踏板质量忽略不计的可变电阻如图,当人站上踏板时,通过电压表显示的读数换算为人的质量,已知随着的变化而变化如图,与踏板上人的质量的关系见图则下列说法不正确的是( )
A. 在一定范围内,越大,越小
B. 当时,的阻值为
C. 当踏板上人的质量为时,
D. 若电压表量程为为保护电压表,该电子体重秤可称的最大质量是
8.已知蓄电池的电压为定值,使用某蓄电池时,电流与电阻是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A. B. C. D.
9.一次函数和反比例函数的图象如图所示,若,则的取值范围是( )
A. 或
B.
C. 或
D. 或
10.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压单位:是气体体积单位:的反比例函数:,能够反映两个变量和函数关系的图象是
( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
11.心理学家研究发现,一般情况下,在一节的课中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数随时间的变化规律如图所示,其中,分别为线段,为双曲线的一部分.上课开始时,注意力指数为,第时,注意力指数为根据图像信息,若开始上课第学生的注意力指数与下课时的注意力指数相等,则的值为 .
12.由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值始终保持,发现通过滑动变阻器的电流与滑动变阻器的电阻成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过,则滑动变阻器阻值的范围是 .
13.某气球内充满了一定质量的气体,当温度不变的条件下,气球内气体的气压是气球体积的反比例函数,且当时,当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .
14.你吃过拉面吗实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度是面条的粗细横截面积的反比例函数,其图像如图所示,则当面条粗时,面条的总长度是
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
某校对教室采取喷洒药物的方式进行消毒,在消毒过程中,先进行的药物喷洒,接着封闭教室,然后打开门窗进行通风.教室内每立方米空气中的含药量与药物在空气中的持续时间之间的函数关系如图所示,在打开门窗通风前分别满足两个一次函数关系,在通风后满足反比例函数关系.
求药物喷洒后空气中的含药量与药物在空气中的持续时间之间的函数表达式.
如果室内空气中的含药量不低于且持续时间不低于才能有效消毒,请通过计算说明此次消毒是否有效.
16.本小题分
已知某品牌运动鞋每双进价元,为求合适的销售价格进行了天的试销,试销情况如下表:
试销天数 第天 第天 第天 第天
售价元双
销售量双
表中数据,满足什么函数表达式?请求出这个函数表达式.
若每天的销售利润为元,则单价应定为多少?
17.本小题分
某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚里温度随时间时变化的函数图像,其中段是恒温阶段,段是双曲线的一部分.请根据图中信息解答下列问题:
求的值.
求恒温系统在一天内保持大棚里温度在及以上的时长.
18.本小题分
实验数据显示,一般成人喝毫升某品牌白酒后,血液中酒精含量毫克百毫升关于时间时变化的图像如图所示图像由线段与部分双曲线组成国家规定,车辆驾驶人员血液中的酒精含量大于或等于毫克百毫升时属于“酒后驾驶”,不能驾车上路.
求部分双曲线的函数表达式;
参照上述数学模型,假设某驾驶员晚上在家喝完毫升该品牌白酒,第二天早上能否驾车去上班?请说明理由.
19.本小题分
方方驾驶小汽车从地匀速行驶到地,行驶里程为千米,设小汽车的行驶时间为时,行驶速度为千米时,且全程速度限定为不超过千米时.
求关于的函数表达式;
方方上午点驾驶小汽车从地出发.
方方需在当天点分至点含点分和点间到达地,求小汽车行驶速度的范围;
方方能否在当天点分前到达地?说明理由.
20.本小题分
某蓄水池员工对一蓄水池进行排水,该蓄水池每小时的排水量与排完水池中的水所用的时间之间的函数关系图像如图所示.
该蓄水池的蓄水量为 ;
如果每小时排水量不超过,那么排完水池中的水所用的时间满足的条件是 .
由于该蓄水池员工有其他任务,为了提前排完水池中的水,需将原计划每小时的排水量增加,求原计划每小时的排水量是多少立方米?
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】略
3.【答案】
【解析】【分析】
本题考查了反比例函数的图象上点的坐标特征,结合实际含义理解图象上点的坐标含义是解题的关键.
根据题意可知的值即为该校的优秀人数,再根据图象即可确定丙校的优秀人数最多.
【解答】
解:根据题意,可知的值即为该校的优秀人数,
描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,
乙、丁两所学校的优秀人数相同,
点丙在反比例函数图象上面,
丙校的的值最大,即优秀人数最多,
故选:.
4.【答案】
【解析】【分析】
本题考查反比例函数的应用、一次函数的应用等知识,解题的关键是读懂图象信息,属于中考常考题型.
利用图中信息一一判断即可
解:、正确不符合题意.
B、由题意时,,室内空气中的含药量不低于的持续时间达到了,正确,不符合题意
C、时,或,,故本选项错误,符合题意
D、当时,函数关系式为,时,当时,函数关系式为,时,,故
当室内空气中的含药量低于时,对人体才是安全的,所以从室内空气中的含药量达到开始,需经过后,学
生才能进入室内,正确不符合题意,
故选:.
5.【答案】
【解析】解:由图象猜测与之间的函数关系为反比例函数.
所以设,
把,代入求得,
,
将其余各点代入验证均适合,
与的函数关系式为,
把代入,得,
当弹簧测力计的示数为时,弹簧测力计与点的距离是,
随着弹簧测力计与点的距离不断增大,弹簧测力计上的示数不断减小.
故选:.
仔细观察表格,在坐标系中分别描出各点,并平滑曲线连接这些点,即可画出函数图象;观察所画图形,回想常见几种函数的图象特征,即可判断出函数类型,利用待定系数法求出函数关系式;把代入上面所得关系式求解,并根据函数的性质判断弹簧秤与点的距离不断增大时的弹簧测力计示数变化情况.
此题考查的是反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
6.【答案】
【解析】解:设,
图象过,
,
,
当电阻为时,电流为:.
故选:.
根据函数图象可设,再将代入即可得出函数关系式,从而解决问题.
本题考查了反比例函数的应用,关键是掌握函数图象上点的坐标必能满足解析式.
7.【答案】
【解析】解:图中随的增大而减小,
在一定范围内,越大,越小.
A正确,不符合题意;
图中的图象经过点,
当时,的阻值为.
B正确,不符合题意;
当时,,时,对应的是,
踏板上人的质量为时,,错误.
符合题意.
,
随的增大而减小.
的最小值为,
的最大值为.
若电压表量程为为保护电压表,该电子体重秤可称的最大质量是.
D正确,不符合题意.
故选:.
根据图中随的增大而减小可得选项正确;图中的图象经过点,可得选项B正确;把代入图三可得为,而时,对应的是,故C错误;根据图三可得随的增大而减小,所用求的最大值,找到的最小值代入即可求得最大该电子体重秤可称的最大质量.
本题综合考查一次函数与反比例函数的应用.结合题意,理解两种函数表达式的意义及性质是解决本题的关键.
8.【答案】
【解析】略
9.【答案】
【解析】解:根据函数图象可知,当或时,一次函数图象在反比例函数图象的上方,
当时,的取值范围是:或.
故选:.
当一次函数的值大于反比例函数的值时,直线在双曲线的上方,根据图象可得出当时,的取值范围.
此题主要考查了反比例函数与一次函数的交点问题,正确利用函数图象分析是解题关键.
10.【答案】
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】略
13.【答案】略
【解析】略
14.【答案】
【解析】略
15.【答案】【小题】
解:当时,设,将点代入,得,解得,所以;当时,设,将点,代入,得解得所以;当时,设,将点代入,得,所以所以所求函数表达式为
【小题】
令,解得;令,解得因为,所以此次消毒有效.
【解析】 见答案
见答案
16.【答案】【小题】
解:由题表中数据,得,所以是的反比例函数,这个函数表达式为.
【小题】
根据题意,得,解得经检验,是原方程的根,所以单价应定为元双.
答:若每天的销售利润为元,则其单价应定为元双.
【解析】 见答案
见答案
17.【答案】【小题】
解:将点代入,得.
【小题】
设开启段的函数表达式为将点,代入,得解得所以开启段的函数表达式为将代入,得将代入,得所以.
答:恒温系统在一天内保持大棚里温度在及以上的时长为.
【解析】 见答案
见答案
18.【答案】【小题】
解:依题意,直线过,则直线的函数表达式为,
当时,,即,
设双曲线的函数表达式为,将点代入,得,
部分双曲线的函数表达式为
【小题】
不能.理由如下:
由,得当时,,
从晚上到第二天早上时间间距为小时,
,驾驶员第二天早上不能驾车去上班.
【解析】 见答案
见答案
19.【答案】【小题】
解:,且全程速度限定为不超过千米时,
关于的函数表达式为.
【小题】
点至点分时长为小时,点至点时长为小时,,将代入,得;将代入,得.
小汽车行驶速度的范围为千米时千米时.
方方不能在当天点分前到达地.理由如下:
点至点分时长为小时,.
故方方不能在当天点分前到达地.
【解析】 见答案
见答案
20.【答案】【小题】
【小题】
【小题】
解:设原计划每小时的排水量为,则实际每小时的排水量为,根据题意,得,
解得经检验,是原方程的解,且符合题意.
答:原计划每小时的排水量是.
【解析】 见答案
见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
