人教版数学九年级上册第二十三章 旋转四步探究案
文档属性
| 名称 | 人教版数学九年级上册第二十三章 旋转四步探究案 |  | |
| 格式 | zip | ||
| 文件大小 | 312.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-23 19:44:40 | ||
图片预览



文档简介
第二十三章 旋转
23.1图形的旋转(1)
学习目标
1、掌握旋转的定义以及相关概念
2、理解旋转的基本性质
3、利用性质解决相关问题。
学习重点:
1. 旋转相关概念以及性质
学习难点:
1. 利用性质解决相关问题。
教学流程
【导课】
自学教材P59并填空:
把一个平面图形___着平面内某一点O__ ( http: / / www.21cnjy.com )___一个角度,就叫做图形的旋转,点O叫做_________,转动的角叫做________。因此,旋转的决定因素是_________和_________。
【阅读质疑 自主探究】
认真阅读教材第56页----第58页,完成下列问题:
旋转的定义(一).自学教材P56并填空:
1、把一个平面图形___着平面内某一点O_ ( http: / / www.21cnjy.com )____一个角度,就叫做图形的旋转,点O叫做_________,转动的角叫做________。因此,旋转的决定因素是_________和_________。
(二).自学检测:
1.钟表的分针匀速旋转一周需要60分.(1)指出它的旋转中心;(2)经过20分,分针旋转了_________度.
2.如图,如果把钟表的指针看做三角形OAB ( http: / / www.21cnjy.com ),它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:(1)旋转中心是______旋转角是__________(2)经过旋转,点A、B分别移动______________
3.如图:ABC是等边三 ( http: / / www.21cnjy.com )角形,D是BC上一点,ABD经过旋转后到达ACE的位置。(1)旋转中心是_______(2)旋转了_______度.(3)如果M是AB的中点,那么经过上述旋转后,点M转到了________________.
【多元互动 合作探究】
1.下列现象中属于旋转的有________________①地下水位逐年下降;
②传送带的移动;③方向盘的转动;④水龙头的转动;⑤钟摆的运动;⑥荡秋千
2.等边三角形至少旋转__________度才能与自身重合。
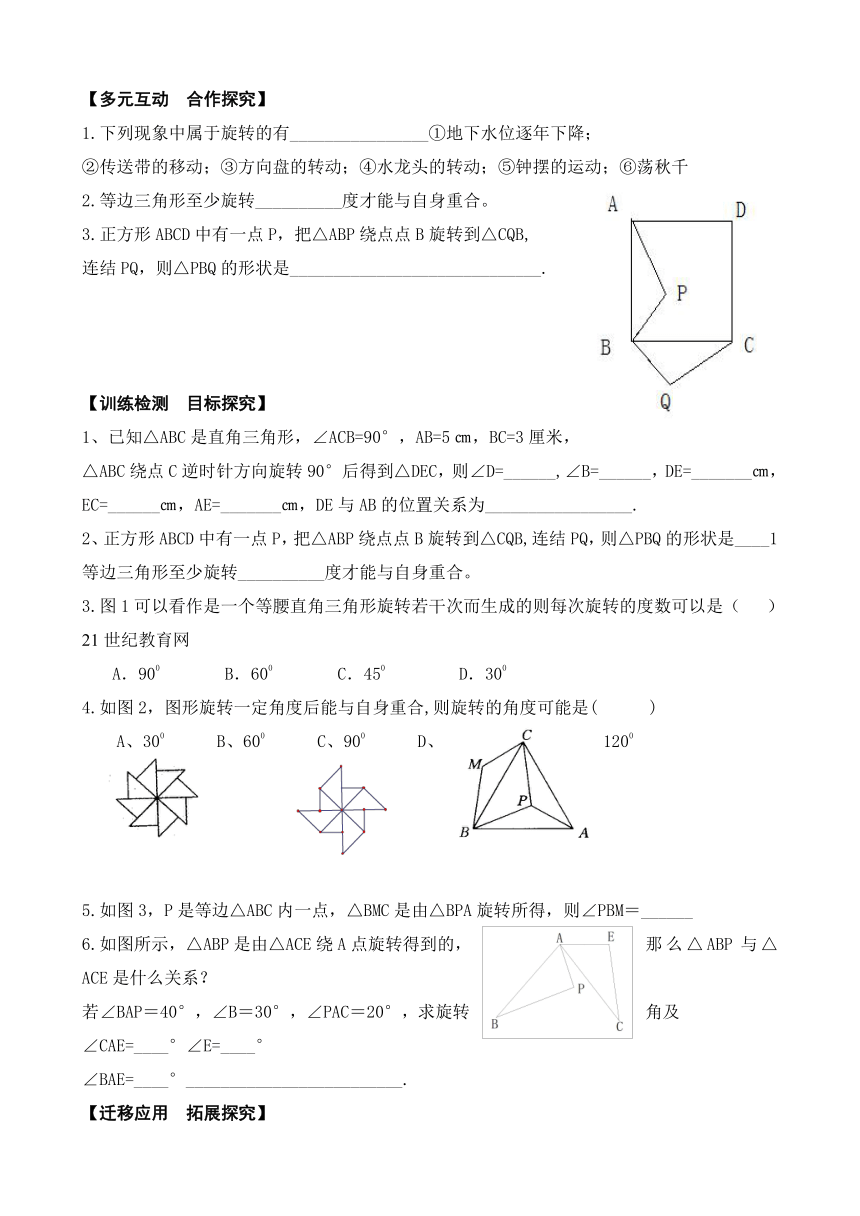
3.正方形ABCD中有一点P,把△ABP绕点点B旋转到△CQB,
连结PQ,则△PBQ的形状是_____________________________.
【训练检测 目标探究】
1、已知△ABC是直角三角形,∠ACB ( http: / / www.21cnjy.com )=90°,AB=5㎝,BC=3厘米,△ABC绕点C逆时针方向旋转90°后得到△DEC,则∠D=______,∠B=______,DE=_______㎝,EC=______㎝,AE=_______㎝,DE与AB的位置关系为_________________.
2、正方形ABCD中有一点P,把△ ( http: / / www.21cnjy.com )ABP绕点点B旋转到△CQB,连结PQ,则△PBQ的形状是____1 等边三角形至少旋转__________度才能与自身重合。
3.图1可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是( )21世纪教育网
A.900 B.600 C.450 D.300
4.如图2,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A、300 B、600 C、900 D、1200
5.如图3,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=______
6.如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系?
若∠BAP=40°,∠B=30°,∠PAC=20°,求旋转角及
∠CAE=____°∠E=____°
∠BAE=____°_________________________.
【迁移应用 拓展探究】
1.钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了_________度.
2.如图,如果把钟表的指针看做三角形OAB,
它绕O点按顺时针方向旋转得到△OEF,在这
个旋转过程中:(1)旋转中心是______旋转
角是__________(2)经过旋转,点A、B分
别移动到_______.
3.如图:ABC是等边三角形,D是BC上一点,ABD
经过旋转后到达ACE的位置。
(1)旋转中心是_______。
旋转了_______度.
(3)如果M是AB的中点,那么
经过上述旋转后,点M转到了________________.
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.1 图形的旋转(二)
学习目标
1、理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;
2、理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.
学习重点:
1. 图形的旋转的基本性质及其应用.
学习难点:
1. 运用操作实验几何得出图形的旋转的三条基本性质.
教学流程
【导课】
学生口答.
1.什么叫旋转?什么叫旋转中心?什么叫旋转角?
2.什么叫旋转的对应点?
【阅读质疑 自主探究】
大家在硬纸板上,挖一个三角形洞,再挖一个小洞
O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出
这个挖掉的三角形洞(△ABC),然后围绕O转动硬纸板,
再描出这个挖掉的三角形洞(△A′B′C′),移开硬纸板,
请大家运用刻度尺和量角器度量线段和有关角,并探索旋
转的性质.
(分组讨论)根据图回答下面问题(一组推荐一人说明)
1.线段OA与OA′,OB与OB′,OC与OC′有什么关系?
2.∠AOA′,∠BOB′,∠COC′有什么关系?
3.△ABC与△A′B′C′形状和大小有什么关系?
总结归纳:旋转的性质
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等.
【多元互动 合作探究】
1.如果两个图形可通过旋转而相互得 ( http: / / www.21cnjy.com )到,则下列说法中正确的有( ).①对应点连线的中垂线必经过旋转中心.②这两个图形大小、形状不变.③对应线段一定相等且平行.④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1个 B.2个 C.3个 D.4个
2.如图,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,
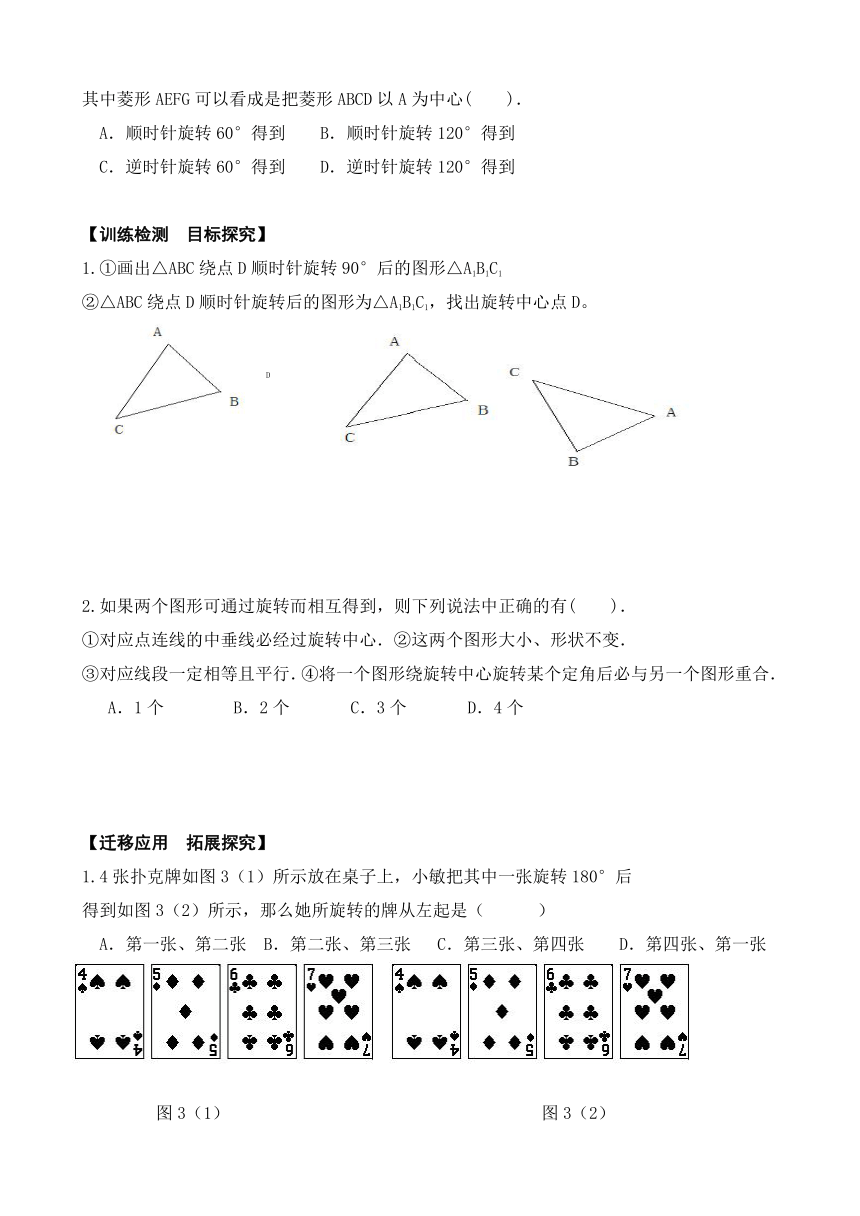
其中菱形AEFG可以看成是把菱形ABCD以A为中心( ).
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
【训练检测 目标探究】
1.①画出△ABC绕点D顺时针旋转90°后的图形△A1B1C1
②△ABC绕点D顺时针旋转后的图形为△A1B1C1,找出旋转中心点D。
D
2.如果两个图形可通过旋转而相互得到,则下列说法中正确的有( ).
①对应点连线的中垂线必经过旋转中心.②这两个图形大小、形状不变.
③对应线段一定相等且平行.④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1个 B.2个 C.3个 D.4个
【迁移应用 拓展探究】
1.4张扑克牌如图3(1)所示放在桌子上,小敏把其中一张旋转180°后
得到如图3(2)所示,那么她所旋转的牌从左起是( )
A.第一张、第二张 B.第二张、第三张 C.第三张、第四张 D.第四张、第一张
图3(1) 图3(2)
2、已知△ABC的BC边的中点D,①画出△ABC绕点D旋转180°的图形△EBC;②四边形ABEC是怎样的四边形?为什么?
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.2.1 中心对称
学习目标
1、了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.
2、利用中心对称、对称中心、关于中心对称点的概念解决一些问题.
学习重点:
1. 从一般旋转中导入中心对称.
学习难点:
1. 利用中心对称、对称中心、关于中心对称点的概念解决一些问题.
教学流程
【导课】
认真阅读教材第62页----第63页,完成下列问题:
1、自学教材P62思考,解答:你有何发现 。
2、把一个图形 那么就说这两个图形关于这个点中心对称。这个点叫_______。
3、结合中心对称的定义回 ( http: / / www.21cnjy.com )答:①中心对称的图形有____个;②中心对称是把一个图形绕某一点旋转___°③中心对称揭示了_____个图形中的一种_______关系。
【阅读质疑 自主探究】
(1)把其中一个图案绕点O旋转180°,你有什么发现
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
总结归纳:
像这样把一个图形绕着某一点旋转1 ( http: / / www.21cnjy.com )80度,如果它能够和 另一个图形重合,那么,我们就说这两个图关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
探究新知(二) 旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
第三步,移开三角板.
思考:画出的△ABC与△A′B′C′关 ( http: / / www.21cnjy.com )于点O对称.分别连接对称点AA′、BB′、CC′。点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
( http: / / www.21cnjy.com )
总结归纳:
(1)在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
(2)关于中心对称的两个图形是全等形。
【多元互动 合作探究】
1、画出△ABC关于点O的中心对称图形。 2、△ABC与△DEF关于点O中心对称,做出对称点。
3、依据第2题的作图,回答:对称点 ( http: / / www.21cnjy.com )是_____,相等的线段有________________________________________.△ABC与△DEF是______形,点A、B、C的对称点分别为___________________.
4、下列说法错误的是 ( )
A.中心对称图形一定是旋转对称图形
B.轴对称图形不一定是中心对称图形
C.在成中心对称的两个图形中,连接对称点的线段都被对称中心平分
D.旋转对称图形一定是中心对称图形。
5 ( http: / / www.21cnjy.com )、关于中心对称的两个图形,对应线段的关系是( ).
(A) 平行 (B) 相等 (C) 平行且相等 (D) 相等且平行或在同一直线上
6、关于中心对称的两个图形,对称点的连线____________
7、 如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这两个图形一定关于这一点成____________对称.
8、右图中②③④⑤分别由①图顺时针旋转180°变换而成的是____________。
9、 在右面四个图形中,图形①与___________成轴对称,图形①与图形___________成中心对称.
10、 如右图所示的四组图形中,左边图形与右边图形成中心对称的有__________组.
11、如图: 请你在右图的正方形格纸中,画出线段AB关于点O成中心对称的图形。
【训练检测 目标探究】
1、点的中心对称点的作法
以点O为对称中心,作出点A的对称点A′;
2、线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段点A′B′
3/如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′。
( http: / / www.21cnjy.com )
【迁移应用 拓展探究】
一、选择题
1.下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形
C.直角梯形 D.两条相交直线
2.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
3.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
( http: / / www.21cnjy.com )
二、填空题
1.关于中心对称的两个图形,对称点所连线段都经过__________,而且被对称中心所________.
2.关于中心对称的两个图形是_________图形.
3.线段既是轴对称图形又是中心对称图形,它的对称轴是_________,它的对称中心是__________.
三、综合提高题
1.分别画出与已知四边形AB ( http: / / www.21cnjy.com )CD成中心对称的四边形,使它们满足以下条件:(1)以顶点A为对称中心,(2)以BC边的中点K为对称中心.
2.如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
( http: / / www.21cnjy.com )
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.2.2 中心对称图形
学习目标
1、了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
2、中心对称图形的有关概念及其它们的运用
学习重点:
1. 区别关于中心对称的两个图形和中心对称图形.
学习难点:
1. 中心对称图形的有关概念及其它们的运用
教学流程
【导课】
1.关于中心对称的两个图形具有什么性质?
2.(学生活动)作图题.
(1)作出线段AO关于O点的对称图形,如图所示.
作出三角形AOB关于O点的对称图形,如图所示.
( http: / / www.21cnjy.com )
【阅读质疑 自主探究】
一、探究新知
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
议一议: (1)这些图形有什么共同的特征?
(2)这些图形的不同点在哪?分别绕旋转中心旋转了多少度
总结归纳:
如果一个图形绕一个点旋转 后,能和原来的图形互相 ,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
【多元互动 合作探究】
1、等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( ).
A.1个 B.2个 C. 3个 D.4个
2、 下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3、下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形,是轴对称图形,但不是中心对称图形有( )
A.1个 B.2 C.3个 D.4个
4、下列4个图形中是中心对称图形的有( )
A.1 B.2 C .3 个 D.4个
【训练检测 目标探究】
1、下列命题中的真命题是( )
A、全等的两个图形是中心对称图形. B、关于中心对称的两个图形全等.
C、中心对称图形都是轴对称图形. D、轴对称图形都是中心对称图形.
2、下列图形中,既是轴对称图形又是中心对称图形的是( )
( http: / / www.21cnjy.com )
A、 B、 C、 D、
3下面是两个圆,请按要求在各图中分别添加四个点,使之满足各自要求.
(1)既是中心对称图形, (2)只是中心对称图形,
又是轴对称图形. 不是轴对称图形.
【迁移应用 拓展探究】
1、如下图中,既是中心对称又是轴对称的图案是( ).
2、如图,在矩形ABCD中,对角线交于点O,过点O的BC=3,则图中阴影部分的面积是________________.
3、已知点O是四边形ABCD的对称中心,求证:四边形ABCD是平行四边形。
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.2.3 关于原点对称的点的坐标
学习目标
1、理解点P与点P’关于原点对称时,它们的横纵坐标的关系,
2、掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用;
学习重点:
1. 掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用;
学习难点:
1. 掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用;
教学流程
【导课】
1.什么是平面直角坐标系?
2.怎样在平面直角坐标系内表示一个点的坐标?
3.点P(a,b)关于x轴的对称点的坐标 ,关于y轴对称点
坐标是 。
4.点P(2,3)关于x轴的对称点的坐_________关于Y轴的对称点的坐标是_____.
5.点M(-3,-4)在第___象限,点M到x轴的距离是_____,到Y轴的距离是_____,
原点的距离是______.
【阅读质疑 自主探究】
如图,在直角坐标系中,已知A(-3,1)、
B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、
F(-2,-2),作出A、B、C、D、E、F点关于
原点O的中心对称点,并写出它们的坐标,
并回答:这些坐标与已知点的坐标有什么
关系?
总结:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点P/(-x,-y).
【多元互动 合作探究】
1、在平面直角坐标系xOy中, ( http: / / www.21cnjy.com )已知点A(2,3),若将OA绕原点O逆时针旋转180°得到0A′,则点A′在平面直角坐标系中的位置是在 ( )
(A)第一象限 (B)第二象限 (c)第三象限 (D)第四象限
2、在平面直角坐标系中,点关于原点对称点的坐标是________
3、在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是__________
检测 目标探究】
1、矩形ABCD的对称中心经过原点,点B的坐标为(-2,-3),则点D的坐标为_____________.
2、点M(1-x,1-y)在第二象限,那么点N(1-x,y-1)关于原点对称的点的在第______象限。
3、将△ABC绕点O旋转180°,点A的坐标为(-3,2),则点A的对称点的坐标为__________.
【迁移应用 拓展探究】
1、如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
( http: / / www.21cnjy.com )
2.如果点P(-3,1),那么点P关于原点的对称点P’ 的坐标是P’_____.
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23、旋转复习课导学案
学习目标
1、了解旋转定义;理解旋转的性质;了解中心对称的性质;
2、了解各种中心对称图形;探索图形的变换。
学习重点:
1. 了解旋转定义;理解旋转的性质;了解中心对称的性质;
学习难点:
1. 了解各种中心对称图形;探索图形的变换。
教学流程
【导课】【自主学习下列内容】
1.在平面内,将一个图形绕一个 沿某个方向转动一个 ,这样的图形运动称为旋转。
2.这个 称为 ,转动的 称为 。
3.旋转性质:(1)对应点到旋转中心的 ( http: / / www.21cnjy.com ) 相等;(2)任意一对对应点与旋转中心所连的 都是旋转角;(3)图形上的每一个点都绕旋转中心沿相同方向转动了 的角度.即旋转角 。
4. 在平面内,一个图形绕某个点旋转 ( http: / / www.21cnjy.com ) ,如果旋转前后的图形互相 ,那么这两个图形叫做中心对称,这个点叫做它的 。
5. 中心对称图形上的每一对对应点所连成的线段都被对称中心 。
【阅读质疑 自主探究】【小组合作完成】
6.点P(x,y)关于原点对称的点是________,关于x轴对称的点是______,关于y轴对称的点是_______.
7、请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 。
8、中心对称与中心对称图形两个概念区别和联系
中心对称是 全等图形之间的 ; 中心对称图形是 图形本身成对称的 。
中心对称的两个图形性质:
成中心对称的两个图形是 ;成中心对称的两个图形,对称点的连线都经过 ,并且被对称中心 。
9、下列图形中,是中心图形又 ( http: / / www.21cnjy.com )是轴对称图形的有(1)平行四边形(2)菱形;(3)矩形;(4)正方形;(5)等腰梯形;(6)线段;(7)角;(8)线段;(9)等边三角形;(10)圆;
10、一个平行四边形绕着它对角线的交点旋转90○能够与它本身重合,则该四边形( )
A.矩形 B.菱形 C.正方形 D.无法确定
【多元互动 合作探究】【小组点评】
11、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A. ΔABC和ΔADE B. ΔABC和ΔABD
C. ΔABD和ΔACE D. ΔACE和ΔADE
12、钟表的秒针匀速旋转一周需要60秒 ( http: / / www.21cnjy.com ).20秒内,秒针旋转的角度是 ;分针经过15 分后,分针转过的角度是 ;分针从数字12出发,转过150○,则它指的数字是 ;
13、如图,中,,.
(1)将向右平移个单位长度,
画出平移后的;
(2)画出关于轴对称的;
(3)将绕原点旋转,画出旋转后的;
(4)在,,中,
______与______成轴对称,对称轴是______;______与
______成中心对称,对称中心的坐标是______。
14、如图,△ABC绕着点C顺时针旋转35°
得到△C ,若⊥AC,
则∠A的度数是 。
15、如图,△ABC绕点B逆时针方向旋 ( http: / / www.21cnjy.com )转到△EBF的位置 ,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC= ,旋转角是 。
【训练检测 目标探究】【教师评级】
16、如图,等腰△ABC绕点A旋转到△A ( http: / / www.21cnjy.com )CD的位置。已知∠ABC=80°,则在这个图中,点B的对应点是 ,BC= ,∠ACD= ,旋转中心是 ,旋转角是
【迁移应用 拓展探究】【课外训练】
17、如图,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
布置作业
板书设计
教后反思
授课时间: 累计课时:
A
B
C
D
E
F
5
-5
-2
-3
-4
-1
3
2
4
1
-5
5
-3
-4
4
-2
3
-1
2
1
o
一石激起千层浪
汽车方向盘
铜钱
23.1图形的旋转(1)
学习目标
1、掌握旋转的定义以及相关概念
2、理解旋转的基本性质
3、利用性质解决相关问题。
学习重点:
1. 旋转相关概念以及性质
学习难点:
1. 利用性质解决相关问题。
教学流程
【导课】
自学教材P59并填空:
把一个平面图形___着平面内某一点O__ ( http: / / www.21cnjy.com )___一个角度,就叫做图形的旋转,点O叫做_________,转动的角叫做________。因此,旋转的决定因素是_________和_________。
【阅读质疑 自主探究】
认真阅读教材第56页----第58页,完成下列问题:
旋转的定义(一).自学教材P56并填空:
1、把一个平面图形___着平面内某一点O_ ( http: / / www.21cnjy.com )____一个角度,就叫做图形的旋转,点O叫做_________,转动的角叫做________。因此,旋转的决定因素是_________和_________。
(二).自学检测:
1.钟表的分针匀速旋转一周需要60分.(1)指出它的旋转中心;(2)经过20分,分针旋转了_________度.
2.如图,如果把钟表的指针看做三角形OAB ( http: / / www.21cnjy.com ),它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:(1)旋转中心是______旋转角是__________(2)经过旋转,点A、B分别移动______________
3.如图:ABC是等边三 ( http: / / www.21cnjy.com )角形,D是BC上一点,ABD经过旋转后到达ACE的位置。(1)旋转中心是_______(2)旋转了_______度.(3)如果M是AB的中点,那么经过上述旋转后,点M转到了________________.
【多元互动 合作探究】
1.下列现象中属于旋转的有________________①地下水位逐年下降;
②传送带的移动;③方向盘的转动;④水龙头的转动;⑤钟摆的运动;⑥荡秋千
2.等边三角形至少旋转__________度才能与自身重合。
3.正方形ABCD中有一点P,把△ABP绕点点B旋转到△CQB,
连结PQ,则△PBQ的形状是_____________________________.
【训练检测 目标探究】
1、已知△ABC是直角三角形,∠ACB ( http: / / www.21cnjy.com )=90°,AB=5㎝,BC=3厘米,△ABC绕点C逆时针方向旋转90°后得到△DEC,则∠D=______,∠B=______,DE=_______㎝,EC=______㎝,AE=_______㎝,DE与AB的位置关系为_________________.
2、正方形ABCD中有一点P,把△ ( http: / / www.21cnjy.com )ABP绕点点B旋转到△CQB,连结PQ,则△PBQ的形状是____1 等边三角形至少旋转__________度才能与自身重合。
3.图1可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是( )21世纪教育网
A.900 B.600 C.450 D.300
4.如图2,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A、300 B、600 C、900 D、1200
5.如图3,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=______
6.如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系?
若∠BAP=40°,∠B=30°,∠PAC=20°,求旋转角及
∠CAE=____°∠E=____°
∠BAE=____°_________________________.
【迁移应用 拓展探究】
1.钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了_________度.
2.如图,如果把钟表的指针看做三角形OAB,
它绕O点按顺时针方向旋转得到△OEF,在这
个旋转过程中:(1)旋转中心是______旋转
角是__________(2)经过旋转,点A、B分
别移动到_______.
3.如图:ABC是等边三角形,D是BC上一点,ABD
经过旋转后到达ACE的位置。
(1)旋转中心是_______。
旋转了_______度.
(3)如果M是AB的中点,那么
经过上述旋转后,点M转到了________________.
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.1 图形的旋转(二)
学习目标
1、理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;
2、理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.
学习重点:
1. 图形的旋转的基本性质及其应用.
学习难点:
1. 运用操作实验几何得出图形的旋转的三条基本性质.
教学流程
【导课】
学生口答.
1.什么叫旋转?什么叫旋转中心?什么叫旋转角?
2.什么叫旋转的对应点?
【阅读质疑 自主探究】
大家在硬纸板上,挖一个三角形洞,再挖一个小洞
O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出
这个挖掉的三角形洞(△ABC),然后围绕O转动硬纸板,
再描出这个挖掉的三角形洞(△A′B′C′),移开硬纸板,
请大家运用刻度尺和量角器度量线段和有关角,并探索旋
转的性质.
(分组讨论)根据图回答下面问题(一组推荐一人说明)
1.线段OA与OA′,OB与OB′,OC与OC′有什么关系?
2.∠AOA′,∠BOB′,∠COC′有什么关系?
3.△ABC与△A′B′C′形状和大小有什么关系?
总结归纳:旋转的性质
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等.
【多元互动 合作探究】
1.如果两个图形可通过旋转而相互得 ( http: / / www.21cnjy.com )到,则下列说法中正确的有( ).①对应点连线的中垂线必经过旋转中心.②这两个图形大小、形状不变.③对应线段一定相等且平行.④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1个 B.2个 C.3个 D.4个
2.如图,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,
其中菱形AEFG可以看成是把菱形ABCD以A为中心( ).
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
【训练检测 目标探究】
1.①画出△ABC绕点D顺时针旋转90°后的图形△A1B1C1
②△ABC绕点D顺时针旋转后的图形为△A1B1C1,找出旋转中心点D。
D
2.如果两个图形可通过旋转而相互得到,则下列说法中正确的有( ).
①对应点连线的中垂线必经过旋转中心.②这两个图形大小、形状不变.
③对应线段一定相等且平行.④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1个 B.2个 C.3个 D.4个
【迁移应用 拓展探究】
1.4张扑克牌如图3(1)所示放在桌子上,小敏把其中一张旋转180°后
得到如图3(2)所示,那么她所旋转的牌从左起是( )
A.第一张、第二张 B.第二张、第三张 C.第三张、第四张 D.第四张、第一张
图3(1) 图3(2)
2、已知△ABC的BC边的中点D,①画出△ABC绕点D旋转180°的图形△EBC;②四边形ABEC是怎样的四边形?为什么?
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.2.1 中心对称
学习目标
1、了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.
2、利用中心对称、对称中心、关于中心对称点的概念解决一些问题.
学习重点:
1. 从一般旋转中导入中心对称.
学习难点:
1. 利用中心对称、对称中心、关于中心对称点的概念解决一些问题.
教学流程
【导课】
认真阅读教材第62页----第63页,完成下列问题:
1、自学教材P62思考,解答:你有何发现 。
2、把一个图形 那么就说这两个图形关于这个点中心对称。这个点叫_______。
3、结合中心对称的定义回 ( http: / / www.21cnjy.com )答:①中心对称的图形有____个;②中心对称是把一个图形绕某一点旋转___°③中心对称揭示了_____个图形中的一种_______关系。
【阅读质疑 自主探究】
(1)把其中一个图案绕点O旋转180°,你有什么发现
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
总结归纳:
像这样把一个图形绕着某一点旋转1 ( http: / / www.21cnjy.com )80度,如果它能够和 另一个图形重合,那么,我们就说这两个图关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
探究新知(二) 旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
第三步,移开三角板.
思考:画出的△ABC与△A′B′C′关 ( http: / / www.21cnjy.com )于点O对称.分别连接对称点AA′、BB′、CC′。点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
( http: / / www.21cnjy.com )
总结归纳:
(1)在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
(2)关于中心对称的两个图形是全等形。
【多元互动 合作探究】
1、画出△ABC关于点O的中心对称图形。 2、△ABC与△DEF关于点O中心对称,做出对称点。
3、依据第2题的作图,回答:对称点 ( http: / / www.21cnjy.com )是_____,相等的线段有________________________________________.△ABC与△DEF是______形,点A、B、C的对称点分别为___________________.
4、下列说法错误的是 ( )
A.中心对称图形一定是旋转对称图形
B.轴对称图形不一定是中心对称图形
C.在成中心对称的两个图形中,连接对称点的线段都被对称中心平分
D.旋转对称图形一定是中心对称图形。
5 ( http: / / www.21cnjy.com )、关于中心对称的两个图形,对应线段的关系是( ).
(A) 平行 (B) 相等 (C) 平行且相等 (D) 相等且平行或在同一直线上
6、关于中心对称的两个图形,对称点的连线____________
7、 如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这两个图形一定关于这一点成____________对称.
8、右图中②③④⑤分别由①图顺时针旋转180°变换而成的是____________。
9、 在右面四个图形中,图形①与___________成轴对称,图形①与图形___________成中心对称.
10、 如右图所示的四组图形中,左边图形与右边图形成中心对称的有__________组.
11、如图: 请你在右图的正方形格纸中,画出线段AB关于点O成中心对称的图形。
【训练检测 目标探究】
1、点的中心对称点的作法
以点O为对称中心,作出点A的对称点A′;
2、线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段点A′B′
3/如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′。
( http: / / www.21cnjy.com )
【迁移应用 拓展探究】
一、选择题
1.下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形
C.直角梯形 D.两条相交直线
2.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
3.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
( http: / / www.21cnjy.com )
二、填空题
1.关于中心对称的两个图形,对称点所连线段都经过__________,而且被对称中心所________.
2.关于中心对称的两个图形是_________图形.
3.线段既是轴对称图形又是中心对称图形,它的对称轴是_________,它的对称中心是__________.
三、综合提高题
1.分别画出与已知四边形AB ( http: / / www.21cnjy.com )CD成中心对称的四边形,使它们满足以下条件:(1)以顶点A为对称中心,(2)以BC边的中点K为对称中心.
2.如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
( http: / / www.21cnjy.com )
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.2.2 中心对称图形
学习目标
1、了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
2、中心对称图形的有关概念及其它们的运用
学习重点:
1. 区别关于中心对称的两个图形和中心对称图形.
学习难点:
1. 中心对称图形的有关概念及其它们的运用
教学流程
【导课】
1.关于中心对称的两个图形具有什么性质?
2.(学生活动)作图题.
(1)作出线段AO关于O点的对称图形,如图所示.
作出三角形AOB关于O点的对称图形,如图所示.
( http: / / www.21cnjy.com )
【阅读质疑 自主探究】
一、探究新知
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
议一议: (1)这些图形有什么共同的特征?
(2)这些图形的不同点在哪?分别绕旋转中心旋转了多少度
总结归纳:
如果一个图形绕一个点旋转 后,能和原来的图形互相 ,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
【多元互动 合作探究】
1、等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( ).
A.1个 B.2个 C. 3个 D.4个
2、 下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3、下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形,是轴对称图形,但不是中心对称图形有( )
A.1个 B.2 C.3个 D.4个
4、下列4个图形中是中心对称图形的有( )
A.1 B.2 C .3 个 D.4个
【训练检测 目标探究】
1、下列命题中的真命题是( )
A、全等的两个图形是中心对称图形. B、关于中心对称的两个图形全等.
C、中心对称图形都是轴对称图形. D、轴对称图形都是中心对称图形.
2、下列图形中,既是轴对称图形又是中心对称图形的是( )
( http: / / www.21cnjy.com )
A、 B、 C、 D、
3下面是两个圆,请按要求在各图中分别添加四个点,使之满足各自要求.
(1)既是中心对称图形, (2)只是中心对称图形,
又是轴对称图形. 不是轴对称图形.
【迁移应用 拓展探究】
1、如下图中,既是中心对称又是轴对称的图案是( ).
2、如图,在矩形ABCD中,对角线交于点O,过点O的BC=3,则图中阴影部分的面积是________________.
3、已知点O是四边形ABCD的对称中心,求证:四边形ABCD是平行四边形。
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23.2.3 关于原点对称的点的坐标
学习目标
1、理解点P与点P’关于原点对称时,它们的横纵坐标的关系,
2、掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用;
学习重点:
1. 掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用;
学习难点:
1. 掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用;
教学流程
【导课】
1.什么是平面直角坐标系?
2.怎样在平面直角坐标系内表示一个点的坐标?
3.点P(a,b)关于x轴的对称点的坐标 ,关于y轴对称点
坐标是 。
4.点P(2,3)关于x轴的对称点的坐_________关于Y轴的对称点的坐标是_____.
5.点M(-3,-4)在第___象限,点M到x轴的距离是_____,到Y轴的距离是_____,
原点的距离是______.
【阅读质疑 自主探究】
如图,在直角坐标系中,已知A(-3,1)、
B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、
F(-2,-2),作出A、B、C、D、E、F点关于
原点O的中心对称点,并写出它们的坐标,
并回答:这些坐标与已知点的坐标有什么
关系?
总结:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点P/(-x,-y).
【多元互动 合作探究】
1、在平面直角坐标系xOy中, ( http: / / www.21cnjy.com )已知点A(2,3),若将OA绕原点O逆时针旋转180°得到0A′,则点A′在平面直角坐标系中的位置是在 ( )
(A)第一象限 (B)第二象限 (c)第三象限 (D)第四象限
2、在平面直角坐标系中,点关于原点对称点的坐标是________
3、在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是__________
检测 目标探究】
1、矩形ABCD的对称中心经过原点,点B的坐标为(-2,-3),则点D的坐标为_____________.
2、点M(1-x,1-y)在第二象限,那么点N(1-x,y-1)关于原点对称的点的在第______象限。
3、将△ABC绕点O旋转180°,点A的坐标为(-3,2),则点A的对称点的坐标为__________.
【迁移应用 拓展探究】
1、如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
( http: / / www.21cnjy.com )
2.如果点P(-3,1),那么点P关于原点的对称点P’ 的坐标是P’_____.
布置作业
板书设计
教后反思
授课时间: 累计课时:
第二十三章 旋转
23、旋转复习课导学案
学习目标
1、了解旋转定义;理解旋转的性质;了解中心对称的性质;
2、了解各种中心对称图形;探索图形的变换。
学习重点:
1. 了解旋转定义;理解旋转的性质;了解中心对称的性质;
学习难点:
1. 了解各种中心对称图形;探索图形的变换。
教学流程
【导课】【自主学习下列内容】
1.在平面内,将一个图形绕一个 沿某个方向转动一个 ,这样的图形运动称为旋转。
2.这个 称为 ,转动的 称为 。
3.旋转性质:(1)对应点到旋转中心的 ( http: / / www.21cnjy.com ) 相等;(2)任意一对对应点与旋转中心所连的 都是旋转角;(3)图形上的每一个点都绕旋转中心沿相同方向转动了 的角度.即旋转角 。
4. 在平面内,一个图形绕某个点旋转 ( http: / / www.21cnjy.com ) ,如果旋转前后的图形互相 ,那么这两个图形叫做中心对称,这个点叫做它的 。
5. 中心对称图形上的每一对对应点所连成的线段都被对称中心 。
【阅读质疑 自主探究】【小组合作完成】
6.点P(x,y)关于原点对称的点是________,关于x轴对称的点是______,关于y轴对称的点是_______.
7、请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 。
8、中心对称与中心对称图形两个概念区别和联系
中心对称是 全等图形之间的 ; 中心对称图形是 图形本身成对称的 。
中心对称的两个图形性质:
成中心对称的两个图形是 ;成中心对称的两个图形,对称点的连线都经过 ,并且被对称中心 。
9、下列图形中,是中心图形又 ( http: / / www.21cnjy.com )是轴对称图形的有(1)平行四边形(2)菱形;(3)矩形;(4)正方形;(5)等腰梯形;(6)线段;(7)角;(8)线段;(9)等边三角形;(10)圆;
10、一个平行四边形绕着它对角线的交点旋转90○能够与它本身重合,则该四边形( )
A.矩形 B.菱形 C.正方形 D.无法确定
【多元互动 合作探究】【小组点评】
11、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A. ΔABC和ΔADE B. ΔABC和ΔABD
C. ΔABD和ΔACE D. ΔACE和ΔADE
12、钟表的秒针匀速旋转一周需要60秒 ( http: / / www.21cnjy.com ).20秒内,秒针旋转的角度是 ;分针经过15 分后,分针转过的角度是 ;分针从数字12出发,转过150○,则它指的数字是 ;
13、如图,中,,.
(1)将向右平移个单位长度,
画出平移后的;
(2)画出关于轴对称的;
(3)将绕原点旋转,画出旋转后的;
(4)在,,中,
______与______成轴对称,对称轴是______;______与
______成中心对称,对称中心的坐标是______。
14、如图,△ABC绕着点C顺时针旋转35°
得到△C ,若⊥AC,
则∠A的度数是 。
15、如图,△ABC绕点B逆时针方向旋 ( http: / / www.21cnjy.com )转到△EBF的位置 ,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC= ,旋转角是 。
【训练检测 目标探究】【教师评级】
16、如图,等腰△ABC绕点A旋转到△A ( http: / / www.21cnjy.com )CD的位置。已知∠ABC=80°,则在这个图中,点B的对应点是 ,BC= ,∠ACD= ,旋转中心是 ,旋转角是
【迁移应用 拓展探究】【课外训练】
17、如图,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
布置作业
板书设计
教后反思
授课时间: 累计课时:
A
B
C
D
E
F
5
-5
-2
-3
-4
-1
3
2
4
1
-5
5
-3
-4
4
-2
3
-1
2
1
o
一石激起千层浪
汽车方向盘
铜钱
同课章节目录
