青岛版九年级数学下册第5章5.6二次函数的图像与一元二次方程(含答案)
文档属性
| 名称 | 青岛版九年级数学下册第5章5.6二次函数的图像与一元二次方程(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 102.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-24 07:42:29 | ||
图片预览

文档简介
青岛版九年级数学下册第5章5.6二次函数的图像与一元二次方程(含答案)
一.选择题(共10小题)
1.(2015 柳州)如图,二次函数y=ax2+bx+c的图象与x轴相交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
A.x<﹣2 B. ﹣2<x<4 C. x>0 D. x>4
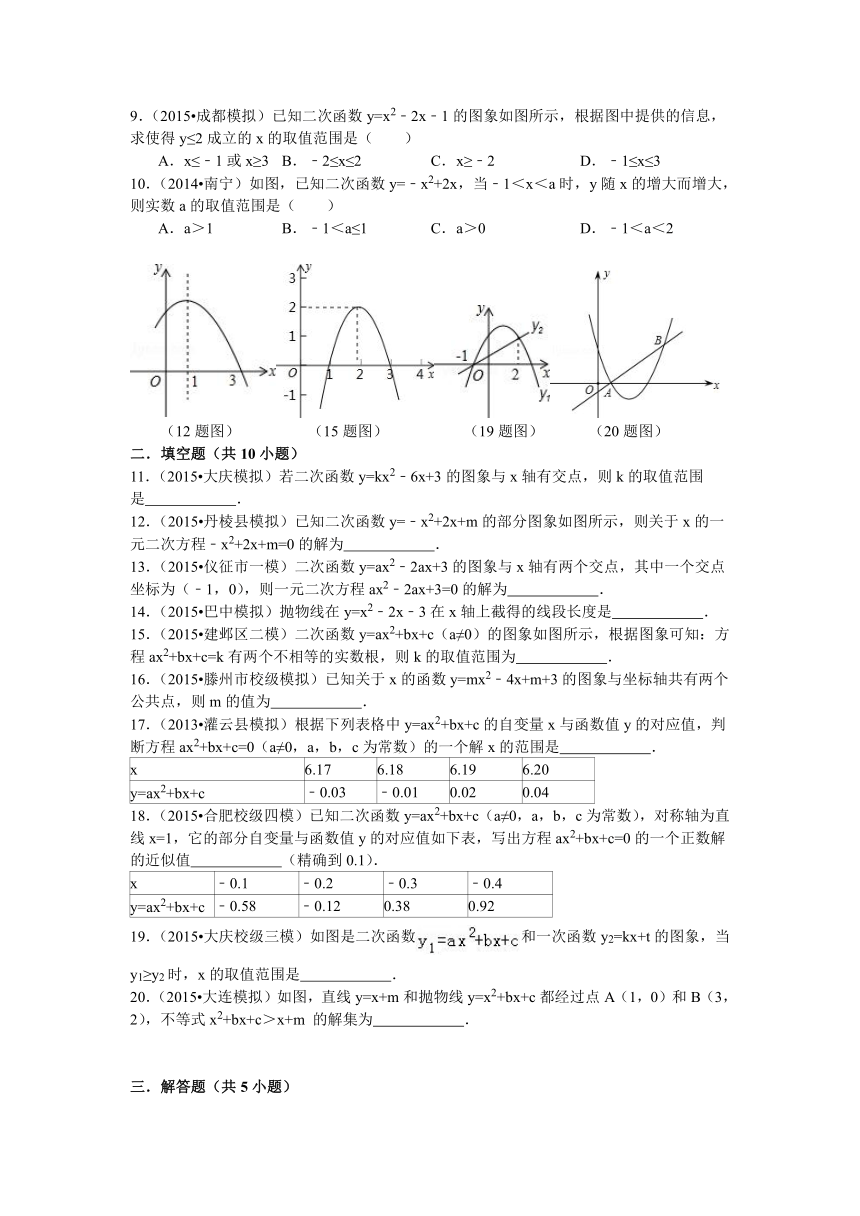
(1题图) (7题图) (9题图) (10题图)
2.(2015 陕西)下列关于二次函数y=ax2﹣2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
A. 没有交点
B. 只有一个交点,且它位于y轴右侧
C. 有两个交点,且它们均位于y轴左侧
D. 有两个交点,且它们均位于y轴右侧
3.(2015 黄冈中学自主招生)已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 0 1 2 3
y 11 1 ﹣1 ﹣1 1 5
且方程ax2+bx+c=0的两根分别为x1,x2(x1<x2),下面说法错误的是( )
A.x=﹣2,y=5 B. 1<x2<2
C.当x1<x<x2时,y>0 D. 当x=时,y有最小值
4.(2015 武汉模拟)二次函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3 B. k<3且k≠0 C. k≤3 D. k≤3且k≠0
5.(2015 杭州模拟)关于x的一元二次方程x2﹣x﹣n=0没有实数根,则抛物线y=x2﹣x﹣n的顶点在( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6.(2015 温州模拟)已知二次函数y=x2+2x﹣10,小明利用计算器列出了下表:
x ﹣4.1 ﹣4.2 ﹣4.3 ﹣4.4
x2+2x﹣10 ﹣1.39 ﹣0.76 ﹣0.11 0.56
那么方程x2+2x﹣10=0的一个近似根是( )
A.﹣4.1 B. ﹣4.2 C. ﹣4.3 D. ﹣4.4
7.(2015 贵港)如图,已知二次函数y1=x2﹣x的图象与正比例函数y2=x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
A.0<x<2 B. 0<x<3 C. 2<x<3 D. x<0或x>3
8.(2015 泸州)若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,则使函数值y>0成立的x的取值范围是( )
A.x<﹣4或x>2 B.﹣4≤x≤2 C. x≤﹣4或x≥2 D. ﹣4<x<2
9.(2015 成都模拟)已知二次函数y=x2﹣2x﹣1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( )
A.x≤﹣1或x≥3 B. ﹣2≤x≤2 C. x≥﹣2 D. ﹣1≤x≤3
10.(2014 南宁)如图,已知二次函数y=﹣x2+2x,当﹣1<x<a时,y随x的增大而增大,则实数a的取值范围是( )
A.a>1 B. ﹣1<a≤1 C. a>0 D. ﹣1<a<2
(12题图) (15题图) (19题图) (20题图)
二.填空题(共10小题)
11.(2015 大庆模拟)若二次函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是 .
12.(2015 丹棱县模拟)已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为 .
13.(2015 仪征市一模)二次函数y=ax2﹣2ax+3的图象与x轴有两个交点,其中一个交点坐标为(﹣1,0),则一元二次方程ax2﹣2ax+3=0的解为 .
14.(2015 巴中模拟)抛物线在y=x2﹣2x﹣3在x轴上截得的线段长度是 .
15.(2015 建邺区二模)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为 .
16.(2015 滕州市校级模拟)已知关于x的函数y=mx2﹣4x+m+3的图象与坐标轴共有两个公共点,则m的值为 .
17.(2013 灌云县模拟)根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是 .
x 6.17 6.18 6.19 6.20
y=ax2+bx+c ﹣0.03 ﹣0.01 0.02 0.04
18.(2015 合肥校级四模)已知二次函数y=ax2+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值 (精确到0.1).
x ﹣0.1 ﹣0.2 ﹣0.3 ﹣0.4
y=ax2+bx+c ﹣0.58 ﹣0.12 0.38 0.92
19.(2015 大庆校级三模)如图是二次函数和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是 .
20.(2015 大连模拟)如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m 的解集为 .
三.解答题(共5小题)
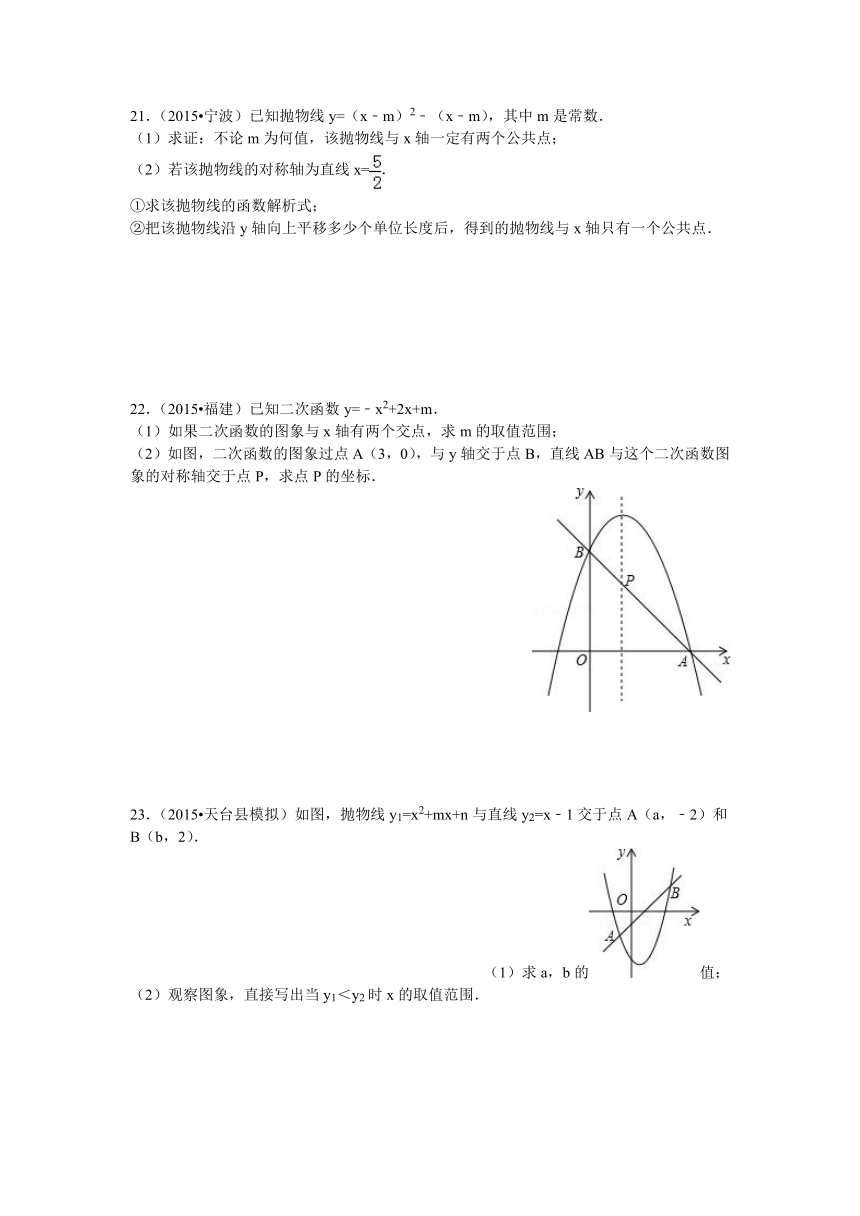
21.(2015 宁波)已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
22.(2015 福建)已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
23.(2015 天台县模拟)如图,抛物线y1=x2+mx+n与直线y2=x﹣1交于点A(a,﹣2)和B(b,2).
(1)求a,b的值;
(2)观察图象,直接写出当y1<y2时x的取值范围.
24.(2015 中山模拟)如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
25.(2015 海伦市校级模拟)如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小?若存在,请求出点P的坐标,若不存在,请说明理由.
青岛版九年级数学下册第5章5.6二次函数的图像与一元二次方程参考答案
一.选择题(共10小题)
1.B 2.D 3.C 4.D 5.A 6.C 7.C 8.D 9.D 10.B
二.填空题(共10小题)
11.k≤3,且k≠0 12.x1=-1或x2=3 13.x1=-1,x2=3 14.4 15.k<2
16.-4,-3,0,1 17.6.18<x<6.19 18.2.2 19.-1≤x≤2 20.x<1或x>3
三.解答题(共5小题)
21.(1)证明:y=(x﹣m)2﹣(x﹣m)=x2﹣(2m+1)x+m2+m,
∵△=(2m+1)2﹣4(m2+m)=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵x=﹣=,∴m=2,
∴抛物线解析式为y=x2﹣5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2﹣5x+6+k,
∵抛物线y=x2﹣5x+6+k与x轴只有一个公共点,
∴△=52﹣4(6+k)=0,∴k=,
即把该抛物线沿y轴向上平移个单位长度后,得到的抛物线与x轴只有一个公共点.
22.解:(1)∵二次函数的图象与x轴有两个交点,∴△=22+4m>0∴m>﹣1;
(2)∵二次函数的图象过点A(3,0),∴0=﹣9+6+m∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
令x=0,则y=3,
∴B(0,3),
设直线AB的解析式为:y=kx+b,
∴,解得:,∴直线AB的解析式为:y=﹣x+3,
∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2,
∴P(1,2).
23.解:(1)由﹣2=a﹣1得,a=﹣1,
由2=b﹣1得,b=3;
(2)由图可知,y1<y2时x的取值范围﹣1<x<3.
24.
解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),
根据题意得 ,解得:,
所以二次函数的解析式为:y=﹣x2﹣2x+3;
(2)如图,一次函数值大于二次函数值的x的取值范围是:x<﹣2或x>1.
(3)∵对称轴:x=﹣1.∴D(﹣2,3);
设直线BD:y=mx+n 代入B(1,0),D(﹣2,3):
,解得:,故直线BD的解析式为:y=﹣x+1,
把x=0代入求得E(0,1)
∴OE=1,
又∵AB=4
∴S△ADE=×4×3﹣×4×1=4.
(24题图) (25题图)
25.解:(1)∵OA=2,OC=3,
∴A(﹣2,0),C(0,3),
代入抛物线解析式得:,解得:b=,c=3,
则抛物线解析式为y=﹣x2+x+3;
(2)连接AD,交对称轴于点P,则P为所求的点,
设直线AD解析式为y=mx+n,
把A(﹣2,0),D(2,2)代入得:,解得:m=,n=1,
∴直线AD解析式为y=x+1,
对称轴为直线x=,
当x=时,y=,
则P坐标为(,).
一.选择题(共10小题)
1.(2015 柳州)如图,二次函数y=ax2+bx+c的图象与x轴相交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
A.x<﹣2 B. ﹣2<x<4 C. x>0 D. x>4
(1题图) (7题图) (9题图) (10题图)
2.(2015 陕西)下列关于二次函数y=ax2﹣2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
A. 没有交点
B. 只有一个交点,且它位于y轴右侧
C. 有两个交点,且它们均位于y轴左侧
D. 有两个交点,且它们均位于y轴右侧
3.(2015 黄冈中学自主招生)已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 0 1 2 3
y 11 1 ﹣1 ﹣1 1 5
且方程ax2+bx+c=0的两根分别为x1,x2(x1<x2),下面说法错误的是( )
A.x=﹣2,y=5 B. 1<x2<2
C.当x1<x<x2时,y>0 D. 当x=时,y有最小值
4.(2015 武汉模拟)二次函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3 B. k<3且k≠0 C. k≤3 D. k≤3且k≠0
5.(2015 杭州模拟)关于x的一元二次方程x2﹣x﹣n=0没有实数根,则抛物线y=x2﹣x﹣n的顶点在( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6.(2015 温州模拟)已知二次函数y=x2+2x﹣10,小明利用计算器列出了下表:
x ﹣4.1 ﹣4.2 ﹣4.3 ﹣4.4
x2+2x﹣10 ﹣1.39 ﹣0.76 ﹣0.11 0.56
那么方程x2+2x﹣10=0的一个近似根是( )
A.﹣4.1 B. ﹣4.2 C. ﹣4.3 D. ﹣4.4
7.(2015 贵港)如图,已知二次函数y1=x2﹣x的图象与正比例函数y2=x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
A.0<x<2 B. 0<x<3 C. 2<x<3 D. x<0或x>3
8.(2015 泸州)若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,则使函数值y>0成立的x的取值范围是( )
A.x<﹣4或x>2 B.﹣4≤x≤2 C. x≤﹣4或x≥2 D. ﹣4<x<2
9.(2015 成都模拟)已知二次函数y=x2﹣2x﹣1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是( )
A.x≤﹣1或x≥3 B. ﹣2≤x≤2 C. x≥﹣2 D. ﹣1≤x≤3
10.(2014 南宁)如图,已知二次函数y=﹣x2+2x,当﹣1<x<a时,y随x的增大而增大,则实数a的取值范围是( )
A.a>1 B. ﹣1<a≤1 C. a>0 D. ﹣1<a<2
(12题图) (15题图) (19题图) (20题图)
二.填空题(共10小题)
11.(2015 大庆模拟)若二次函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是 .
12.(2015 丹棱县模拟)已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为 .
13.(2015 仪征市一模)二次函数y=ax2﹣2ax+3的图象与x轴有两个交点,其中一个交点坐标为(﹣1,0),则一元二次方程ax2﹣2ax+3=0的解为 .
14.(2015 巴中模拟)抛物线在y=x2﹣2x﹣3在x轴上截得的线段长度是 .
15.(2015 建邺区二模)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为 .
16.(2015 滕州市校级模拟)已知关于x的函数y=mx2﹣4x+m+3的图象与坐标轴共有两个公共点,则m的值为 .
17.(2013 灌云县模拟)根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是 .
x 6.17 6.18 6.19 6.20
y=ax2+bx+c ﹣0.03 ﹣0.01 0.02 0.04
18.(2015 合肥校级四模)已知二次函数y=ax2+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值 (精确到0.1).
x ﹣0.1 ﹣0.2 ﹣0.3 ﹣0.4
y=ax2+bx+c ﹣0.58 ﹣0.12 0.38 0.92
19.(2015 大庆校级三模)如图是二次函数和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是 .
20.(2015 大连模拟)如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m 的解集为 .
三.解答题(共5小题)
21.(2015 宁波)已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
22.(2015 福建)已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
23.(2015 天台县模拟)如图,抛物线y1=x2+mx+n与直线y2=x﹣1交于点A(a,﹣2)和B(b,2).
(1)求a,b的值;
(2)观察图象,直接写出当y1<y2时x的取值范围.
24.(2015 中山模拟)如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
25.(2015 海伦市校级模拟)如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小?若存在,请求出点P的坐标,若不存在,请说明理由.
青岛版九年级数学下册第5章5.6二次函数的图像与一元二次方程参考答案
一.选择题(共10小题)
1.B 2.D 3.C 4.D 5.A 6.C 7.C 8.D 9.D 10.B
二.填空题(共10小题)
11.k≤3,且k≠0 12.x1=-1或x2=3 13.x1=-1,x2=3 14.4 15.k<2
16.-4,-3,0,1 17.6.18<x<6.19 18.2.2 19.-1≤x≤2 20.x<1或x>3
三.解答题(共5小题)
21.(1)证明:y=(x﹣m)2﹣(x﹣m)=x2﹣(2m+1)x+m2+m,
∵△=(2m+1)2﹣4(m2+m)=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵x=﹣=,∴m=2,
∴抛物线解析式为y=x2﹣5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2﹣5x+6+k,
∵抛物线y=x2﹣5x+6+k与x轴只有一个公共点,
∴△=52﹣4(6+k)=0,∴k=,
即把该抛物线沿y轴向上平移个单位长度后,得到的抛物线与x轴只有一个公共点.
22.解:(1)∵二次函数的图象与x轴有两个交点,∴△=22+4m>0∴m>﹣1;
(2)∵二次函数的图象过点A(3,0),∴0=﹣9+6+m∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
令x=0,则y=3,
∴B(0,3),
设直线AB的解析式为:y=kx+b,
∴,解得:,∴直线AB的解析式为:y=﹣x+3,
∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2,
∴P(1,2).
23.解:(1)由﹣2=a﹣1得,a=﹣1,
由2=b﹣1得,b=3;
(2)由图可知,y1<y2时x的取值范围﹣1<x<3.
24.
解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),
根据题意得 ,解得:,
所以二次函数的解析式为:y=﹣x2﹣2x+3;
(2)如图,一次函数值大于二次函数值的x的取值范围是:x<﹣2或x>1.
(3)∵对称轴:x=﹣1.∴D(﹣2,3);
设直线BD:y=mx+n 代入B(1,0),D(﹣2,3):
,解得:,故直线BD的解析式为:y=﹣x+1,
把x=0代入求得E(0,1)
∴OE=1,
又∵AB=4
∴S△ADE=×4×3﹣×4×1=4.
(24题图) (25题图)
25.解:(1)∵OA=2,OC=3,
∴A(﹣2,0),C(0,3),
代入抛物线解析式得:,解得:b=,c=3,
则抛物线解析式为y=﹣x2+x+3;
(2)连接AD,交对称轴于点P,则P为所求的点,
设直线AD解析式为y=mx+n,
把A(﹣2,0),D(2,2)代入得:,解得:m=,n=1,
∴直线AD解析式为y=x+1,
对称轴为直线x=,
当x=时,y=,
则P坐标为(,).
