2023-2024学年初中数学冀教版九年级下册29.4 切线长定理 分层作业 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学冀教版九年级下册29.4 切线长定理 分层作业 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 191.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 18:14:57 | ||
图片预览



文档简介
29.4 切线长定理*
【练基础】
必备知识1 切线长定理
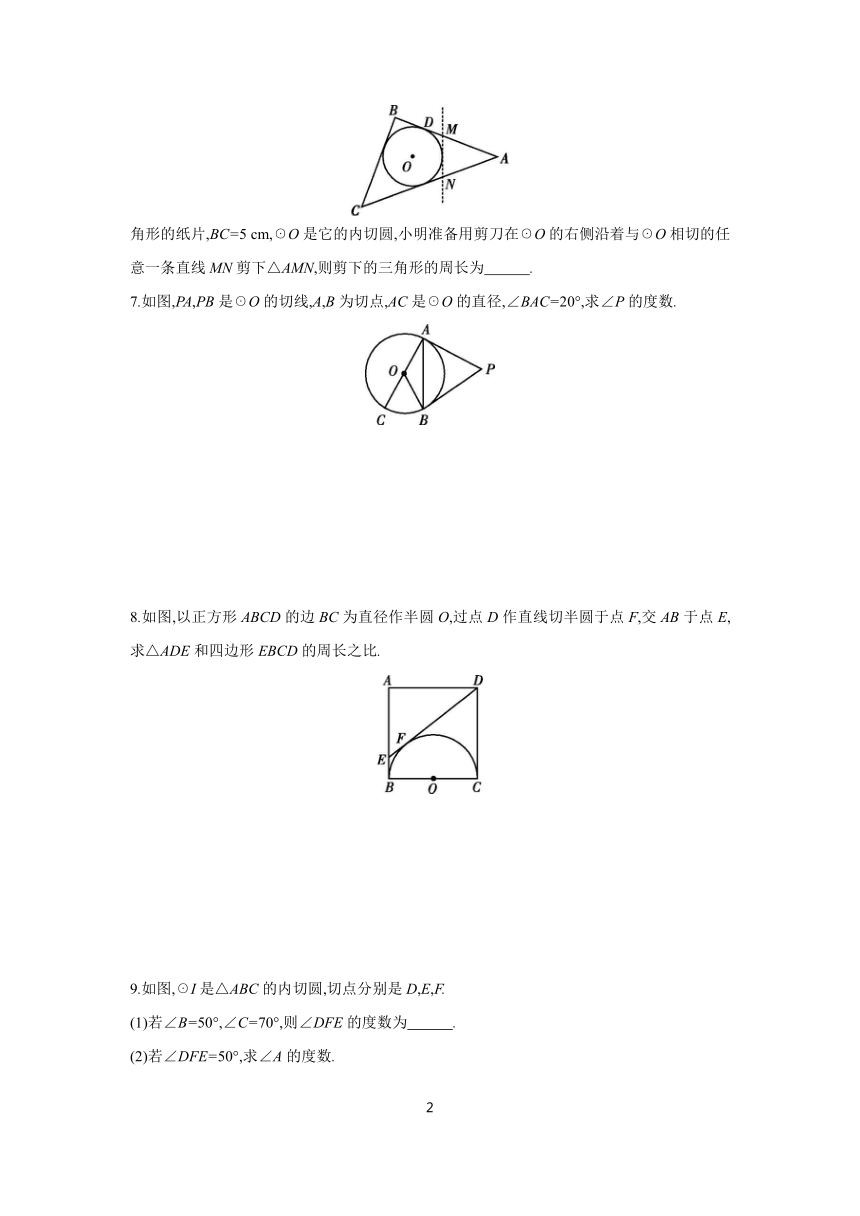
1.如图,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB等于 ( )
A.4 B.8 C.4 D.8
2.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为 ( )
A.32 B.34 C.36 D.38
必备知识2 三角形的内切圆
3.等边三角形ABC的边长为4,则它的内切圆半径的长是 ( )
A.2 B. C.2 D.4
4.在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的面积为 .
【练能力】
5.如图,P为☉O外一点,PA,PB分别切☉O于点A,B,CD切☉O于点E且分别交PA,PB于点C,D,若PA=4,则△PCD的周长为 ( )
A.5 B.7
C.8 D.10
6.如图,△ABC是一张周长为17 cm的三
角形的纸片,BC=5 cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为 .
7.如图,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,∠BAC=20°,求∠P的度数.
8.如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,求△ADE和四边形EBCD的周长之比.
9.如图,☉I是△ABC的内切圆,切点分别是D,E,F.
(1)若∠B=50°,∠C=70°,则∠DFE的度数为 .
(2)若∠DFE=50°,求∠A的度数.
10.课本再现
(1)在☉O中,∠AOB是所对的圆心角,∠C是所对的圆周角,我们在数学课上探索两者之间的关系时,要根据圆心O与∠C的位置关系进行分类.图1是其中一种情况,请你在图2和图3中画出其他两种情况的图形,并从三种位置关系中任选一种情况证明∠C=∠AOB.
知识应用
(2)如图4,若☉O的半径为2,PA,PB分别与☉O相切于点A,B,∠C=60°,求PA的长.
【练素养】
11.如图1,P是☉O外一点,过点P作☉O的两条切线,切点分别为A,B.若∠APB=60°,则点P叫作☉O的切角点.
(1)如图2,☉O的半径是1,点O到直线l的距离为2.若点P是☉O的切角点,且点P在直线l上,请用尺规作出点P.(保留作图痕迹,不写作法)
(2)如图3,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1+,☉O是△ABC的内切圆.若点P是☉O的切角点,且点P在△ABC的边上,求AP的长.
参考答案
练基础
1.B 2.B 3.C 4.4π
练能力
5.C 6.7 cm
7.【解析】根据切线的性质得∠PAC=90°,
所以∠PAB=∠PAC-∠BAC=90°-20°=70°.
根据切线长定理得PA=PB,
所以∠PAB=∠PBA=70°,
所以∠P=180°-70°×2=40°.
8.【解析】根据切线长定理得BE=EF,DF=DC=AD=AB=BC.
设EF=x,DF=y,则在直角△AED中,AE=y-x,AD=CD=y,DE=x+y.
根据勾股定理,得(y-x)2+y2=(x+y)2,∴y=4x,
∴三角形ADE的周长为12x,四边形EBCD的周长为14x.
∴两者周长之比为12x∶14x=6∶7,
故△ADE和四边形EBCD的周长之比为6∶7.
9.【解析】(1)如图,连接ID,IE.
∵∠B=50°,∠C=70°,
∴∠A=60°.
∵☉I是△ABC的内切圆,切点分别是D,E,F,
∴∠IDA=∠IEA=90°,
∴∠DIE=180°-60°=120°,
∴∠DFE的度数为60°.
(2)∵∠DFE=50°,
∴∠DIE=100°.
∵AB,AC分别与☉I相切于点D,E,
∴∠ADI=∠AEI=90°,
∴∠A=80°.
10.【解析】(1)其他两种情况如图1,图2所示.
证明:①如图1,连接CO,并延长CO交☉O于点D.
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO.
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
∴∠ACB=∠AOB.
②如图2,连接CO,并延长CO交☉O于点D.
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO.
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD-∠BOD=2∠ACO-2∠BCO=2∠ACB,
∴∠ACB=∠AOB.
(任选一种即可)
(2)如图3,连接OA,OB,OP.
∵∠C=60°,∴∠AOB=2∠C=120°.
∵PA,PB分别与☉O相切于点A,B,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=∠APB=(180°-120°)=30°.
∵OA=2,∴OP=2OA=4,
∴PA==2.
练素养
11.【解析】(1)如图1,点P即为所求.
(2)∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1+,
∴AB=2+2,AC=3+.
∵☉O是△ABC的内切圆,
设AB,BC,AC分别与☉O相切于点M,N,D,
∴OD⊥AC,ON⊥BC,OM⊥AB,BM=BN,CN=CD,AM=AD.
∵∠ACB=90°,∴四边形ONCD为矩形.
∵OD=ON,∴矩形ONCD为正方形.
设☉O的半径为r,则CN=CD=r,
BN=BM=1+-r,MA=AD=1++r.
∴AC=AD+CD=1++r+r.
即1++r+r=3+.
解得 r=1.
∴CD=1,BM=.
如图2,∵∠B=60°,且BA,BC与☉O分别相切于点M,N,
∴点B是☉O的切角点,即点P与点B重合,此时AP=AB=2+2.
如图3,若☉O的切角点P在线段AB上,PQ与☉O相切于点Q.
由切角点的概念知∠MPQ=60°.
连接MO、QO、PO,有∠PMO=∠PQO=90°.
∵MO、QO是☉O的半径,∴MO=QO.
∵PO=PO,∴Rt△PMO≌Rt△PQO(HL).
∵∠MPO=∠QPO=∠MPQ=30°.
且r=1,∴MP=,
∴AP=BA-BM-MP=2.
如图4,若☉O的切角点P在线段AC上.
与上一种情况类似,计算可得PD=.
则AP=AC-CD-PD=2.
综上所述,AP的长为2+2或2.
2
【练基础】
必备知识1 切线长定理
1.如图,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB等于 ( )
A.4 B.8 C.4 D.8
2.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为 ( )
A.32 B.34 C.36 D.38
必备知识2 三角形的内切圆
3.等边三角形ABC的边长为4,则它的内切圆半径的长是 ( )
A.2 B. C.2 D.4
4.在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的面积为 .
【练能力】
5.如图,P为☉O外一点,PA,PB分别切☉O于点A,B,CD切☉O于点E且分别交PA,PB于点C,D,若PA=4,则△PCD的周长为 ( )
A.5 B.7
C.8 D.10
6.如图,△ABC是一张周长为17 cm的三
角形的纸片,BC=5 cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为 .
7.如图,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,∠BAC=20°,求∠P的度数.
8.如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,求△ADE和四边形EBCD的周长之比.
9.如图,☉I是△ABC的内切圆,切点分别是D,E,F.
(1)若∠B=50°,∠C=70°,则∠DFE的度数为 .
(2)若∠DFE=50°,求∠A的度数.
10.课本再现
(1)在☉O中,∠AOB是所对的圆心角,∠C是所对的圆周角,我们在数学课上探索两者之间的关系时,要根据圆心O与∠C的位置关系进行分类.图1是其中一种情况,请你在图2和图3中画出其他两种情况的图形,并从三种位置关系中任选一种情况证明∠C=∠AOB.
知识应用
(2)如图4,若☉O的半径为2,PA,PB分别与☉O相切于点A,B,∠C=60°,求PA的长.
【练素养】
11.如图1,P是☉O外一点,过点P作☉O的两条切线,切点分别为A,B.若∠APB=60°,则点P叫作☉O的切角点.
(1)如图2,☉O的半径是1,点O到直线l的距离为2.若点P是☉O的切角点,且点P在直线l上,请用尺规作出点P.(保留作图痕迹,不写作法)
(2)如图3,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1+,☉O是△ABC的内切圆.若点P是☉O的切角点,且点P在△ABC的边上,求AP的长.
参考答案
练基础
1.B 2.B 3.C 4.4π
练能力
5.C 6.7 cm
7.【解析】根据切线的性质得∠PAC=90°,
所以∠PAB=∠PAC-∠BAC=90°-20°=70°.
根据切线长定理得PA=PB,
所以∠PAB=∠PBA=70°,
所以∠P=180°-70°×2=40°.
8.【解析】根据切线长定理得BE=EF,DF=DC=AD=AB=BC.
设EF=x,DF=y,则在直角△AED中,AE=y-x,AD=CD=y,DE=x+y.
根据勾股定理,得(y-x)2+y2=(x+y)2,∴y=4x,
∴三角形ADE的周长为12x,四边形EBCD的周长为14x.
∴两者周长之比为12x∶14x=6∶7,
故△ADE和四边形EBCD的周长之比为6∶7.
9.【解析】(1)如图,连接ID,IE.
∵∠B=50°,∠C=70°,
∴∠A=60°.
∵☉I是△ABC的内切圆,切点分别是D,E,F,
∴∠IDA=∠IEA=90°,
∴∠DIE=180°-60°=120°,
∴∠DFE的度数为60°.
(2)∵∠DFE=50°,
∴∠DIE=100°.
∵AB,AC分别与☉I相切于点D,E,
∴∠ADI=∠AEI=90°,
∴∠A=80°.
10.【解析】(1)其他两种情况如图1,图2所示.
证明:①如图1,连接CO,并延长CO交☉O于点D.
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO.
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
∴∠ACB=∠AOB.
②如图2,连接CO,并延长CO交☉O于点D.
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO.
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD-∠BOD=2∠ACO-2∠BCO=2∠ACB,
∴∠ACB=∠AOB.
(任选一种即可)
(2)如图3,连接OA,OB,OP.
∵∠C=60°,∴∠AOB=2∠C=120°.
∵PA,PB分别与☉O相切于点A,B,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=∠APB=(180°-120°)=30°.
∵OA=2,∴OP=2OA=4,
∴PA==2.
练素养
11.【解析】(1)如图1,点P即为所求.
(2)∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1+,
∴AB=2+2,AC=3+.
∵☉O是△ABC的内切圆,
设AB,BC,AC分别与☉O相切于点M,N,D,
∴OD⊥AC,ON⊥BC,OM⊥AB,BM=BN,CN=CD,AM=AD.
∵∠ACB=90°,∴四边形ONCD为矩形.
∵OD=ON,∴矩形ONCD为正方形.
设☉O的半径为r,则CN=CD=r,
BN=BM=1+-r,MA=AD=1++r.
∴AC=AD+CD=1++r+r.
即1++r+r=3+.
解得 r=1.
∴CD=1,BM=.
如图2,∵∠B=60°,且BA,BC与☉O分别相切于点M,N,
∴点B是☉O的切角点,即点P与点B重合,此时AP=AB=2+2.
如图3,若☉O的切角点P在线段AB上,PQ与☉O相切于点Q.
由切角点的概念知∠MPQ=60°.
连接MO、QO、PO,有∠PMO=∠PQO=90°.
∵MO、QO是☉O的半径,∴MO=QO.
∵PO=PO,∴Rt△PMO≌Rt△PQO(HL).
∵∠MPO=∠QPO=∠MPQ=30°.
且r=1,∴MP=,
∴AP=BA-BM-MP=2.
如图4,若☉O的切角点P在线段AC上.
与上一种情况类似,计算可得PD=.
则AP=AC-CD-PD=2.
综上所述,AP的长为2+2或2.
2
