2023-2024学年初中数学冀教版九年级下册29.5 正多边形与圆 分层作业(含答案)
文档属性
| 名称 | 2023-2024学年初中数学冀教版九年级下册29.5 正多边形与圆 分层作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 197.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览


文档简介
29.5 正多边形与圆
【练基础】
必备知识1 正多边形与圆的关系
1.已知正六边形的边长为2,则它的内切圆的半径为 ( )
A.1 B. C.2 D.2
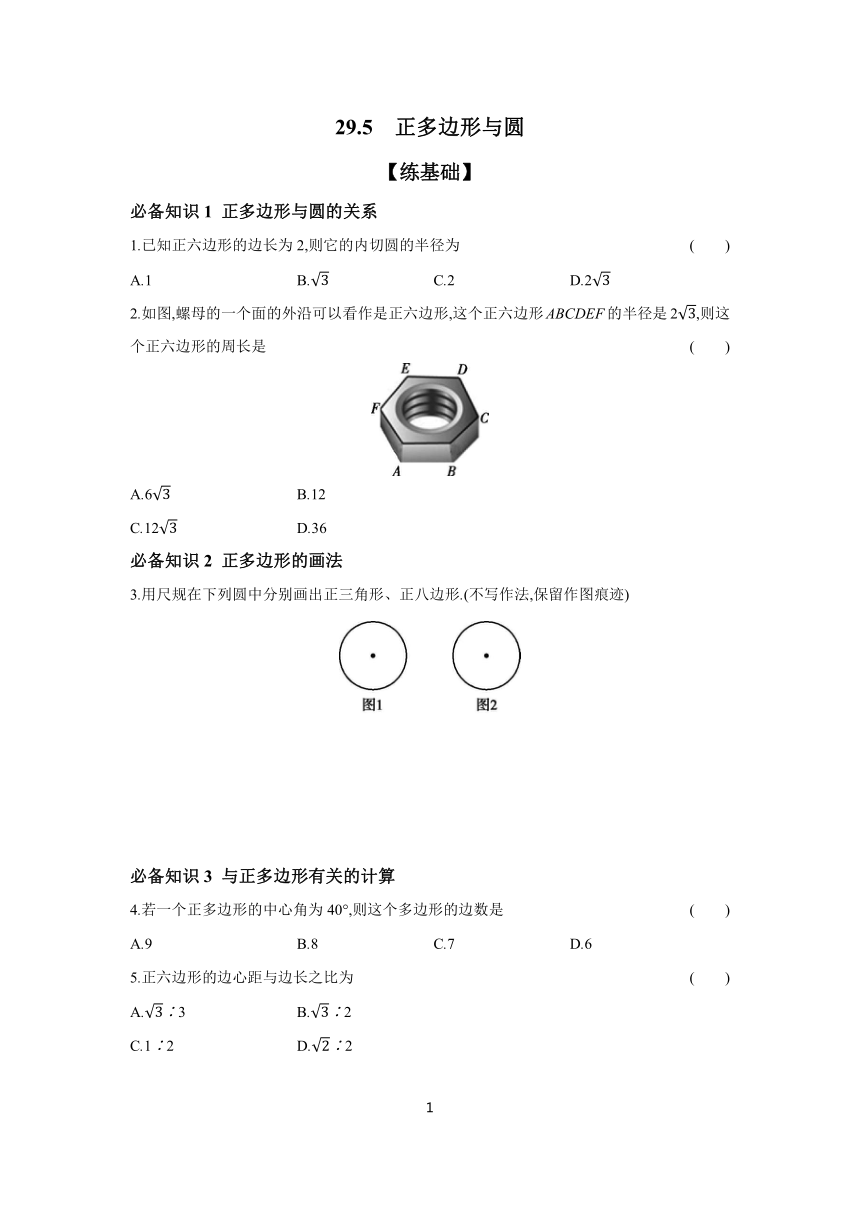
2.如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是2,则这个正六边形的周长是 ( )
A.6 B.12
C.12 D.36
必备知识2 正多边形的画法
3.用尺规在下列圆中分别画出正三角形、正八边形.(不写作法,保留作图痕迹)
必备知识3 与正多边形有关的计算
4.若一个正多边形的中心角为40°,则这个多边形的边数是 ( )
A.9 B.8 C.7 D.6
5.正六边形的边心距与边长之比为 ( )
A.∶3 B.∶2
C.1∶2 D.∶2
【练能力】
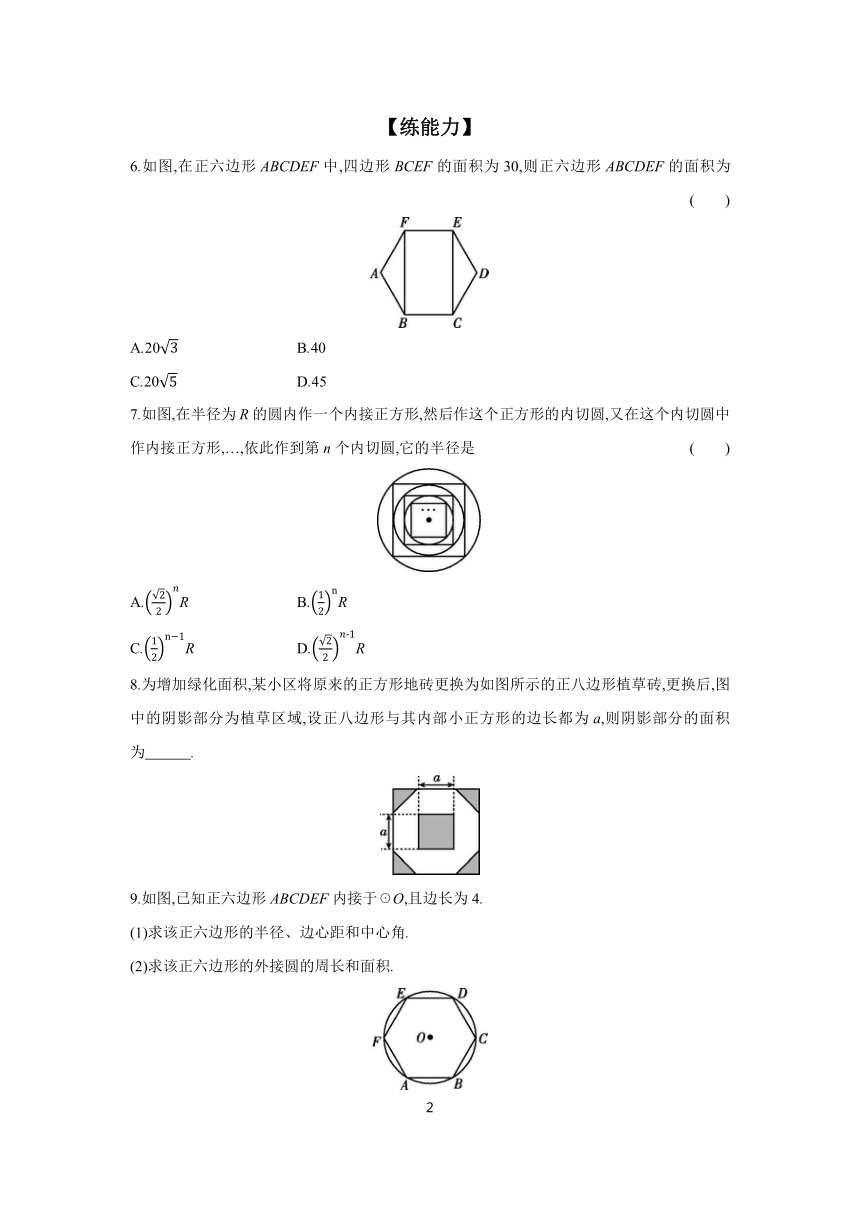
6.如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为 ( )
A.20 B.40
C.20 D.45
7.如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,…,依此作到第n个内切圆,它的半径是 ( )
A.R B.R
C.R D.R
8.为增加绿化面积,某小区将原来的正方形地砖更换为如图所示的正八边形植草砖,更换后,图中的阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为 .
9.如图,已知正六边形ABCDEF内接于☉O,且边长为4.
(1)求该正六边形的半径、边心距和中心角.
(2)求该正六边形的外接圆的周长和面积.
10.如图,这是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.
11.如图,正方形ABCD内接于☉O,P为上一点,连接DP,CP.
(1)∠CPD= °.
(2)若DC=4,CP=2,求DP的长.
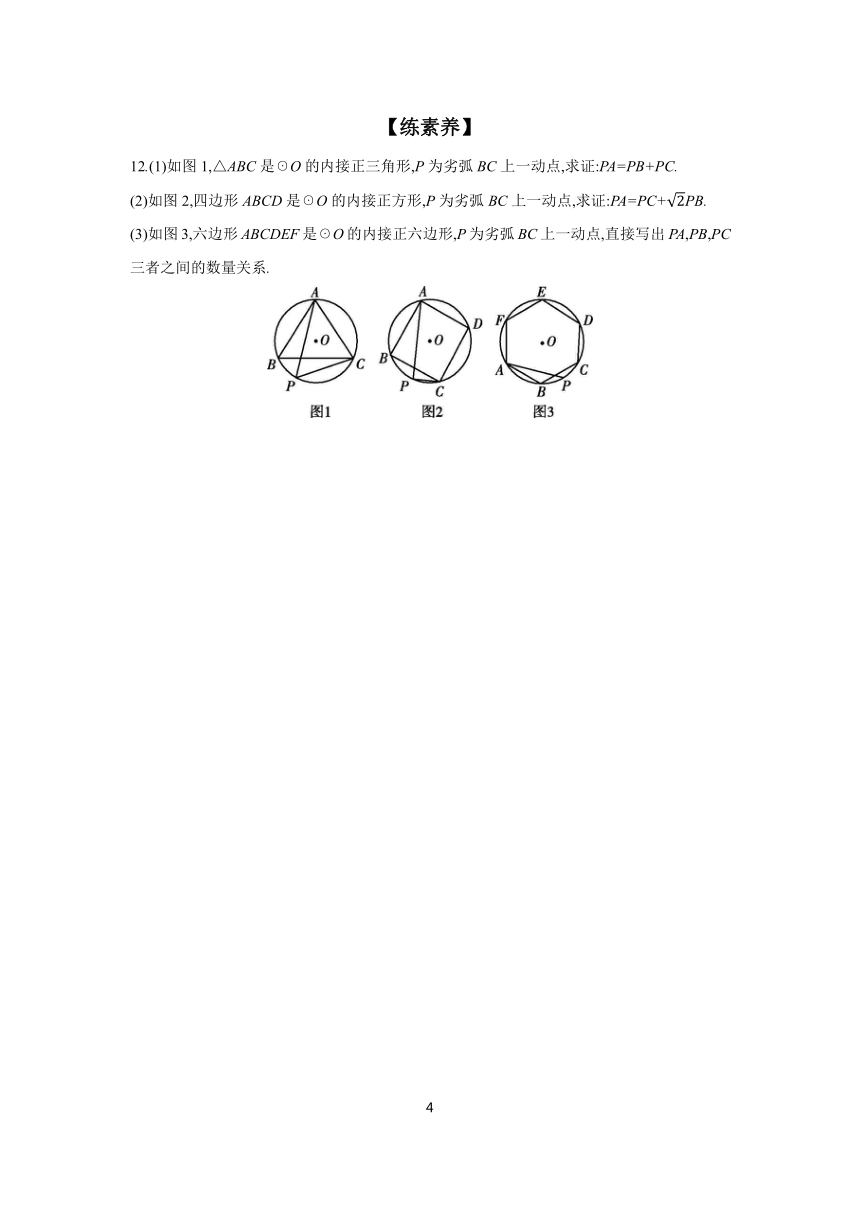
【练素养】
12.(1)如图1,△ABC是☉O的内接正三角形,P为劣弧BC上一动点,求证:PA=PB+PC.
(2)如图2,四边形ABCD是☉O的内接正方形,P为劣弧BC上一动点,求证:PA=PC+PB.
(3)如图3,六边形ABCDEF是☉O的内接正六边形,P为劣弧BC上一动点,直接写出PA,PB,PC三者之间的数量关系.
参考答案
练基础
1.B 2.C
3.【解析】如图1,△BCD即圆的内接正三角形.
如图2,八边形AECHBFDG即圆的内接正八边形.
4.A 5.B
练能力
6.D 7.A 8.2a2
9.【解析】(1)
如图,AB为☉O的内接正六边形的一边,连接OA,OB,过点O作OM⊥AB于点M.
∵六边形ABCDEF为正六边形,
∴OA=OB,中心角∠AOB=×360°=60°,
∴△OAB为等边三角形,
∴半径OA=AB=4.
∵边心距OM⊥AB,
∴∠AOM=∠BOM=30°,AM=AB=2,
∴边心距OM=AM=2.
(2)正六边形的外接圆的周长=2π×OA=8π;
外接圆的面积=π×42=16π.
10.【解析】如图,延长AB,一定交正六边形于格点E,连接CE.
正六边形的边长为1,则其半径是1,则CE=4.
中间间隔一个顶点的两个顶点之间的距离是,
则△BCE的边EC上的高是,
△ACE的边EC上的高是,
则S△ABC=S△AEC-S△BEC=×4×=2.
11.【解析】(1)如图,连接BD.
∵正方形ABCD内接于☉O,P为上一点,
∴∠DBC=45°.∵∠CPD=∠DBC,∴∠CPD=45°,故答案为45.
(2)如图,作CH⊥DP于点H.∵CP=2,∠CPD=45°,∴CH=PH=2.∵DC=4,∴DH==2,∴DP=PH+DH=2+2.
练素养
12.【解析】(1)证明:如图1,连接BP并延长至E,使PE=PC,连接CE.
∵四边形ABPC是☉O的内接四边形,
∴∠BAC+∠BPC=180°.
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°.
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP.
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC.
在△BEC和△APC中,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)证明:如图2,连接BP,过点B作BE⊥PB交PA于点E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,
∴PE=PB.
在△ABE和△CBP中,
∴△ABE≌△CBP(SAS),
∴PC=AE,∴PA=AE+PE=PC+PB.
(3)PA=PC+PB.
提示:如图3,连接PC,过点B作BM⊥AP,在AP上截取AQ=PC,连接BQ.
∵∠BAP=∠BCP,AB=BC,
在△ABQ和△CBP中,
∴△ABQ≌△CBP(SAS),
∴BQ=BP,
∴MP=QM.
又∵∠APB=30°,
∴PM=PB,
∴PQ=PB,
∴PA=PQ+AQ=PC+PB.
2
【练基础】
必备知识1 正多边形与圆的关系
1.已知正六边形的边长为2,则它的内切圆的半径为 ( )
A.1 B. C.2 D.2
2.如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是2,则这个正六边形的周长是 ( )
A.6 B.12
C.12 D.36
必备知识2 正多边形的画法
3.用尺规在下列圆中分别画出正三角形、正八边形.(不写作法,保留作图痕迹)
必备知识3 与正多边形有关的计算
4.若一个正多边形的中心角为40°,则这个多边形的边数是 ( )
A.9 B.8 C.7 D.6
5.正六边形的边心距与边长之比为 ( )
A.∶3 B.∶2
C.1∶2 D.∶2
【练能力】
6.如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为 ( )
A.20 B.40
C.20 D.45
7.如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,…,依此作到第n个内切圆,它的半径是 ( )
A.R B.R
C.R D.R
8.为增加绿化面积,某小区将原来的正方形地砖更换为如图所示的正八边形植草砖,更换后,图中的阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为 .
9.如图,已知正六边形ABCDEF内接于☉O,且边长为4.
(1)求该正六边形的半径、边心距和中心角.
(2)求该正六边形的外接圆的周长和面积.
10.如图,这是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.
11.如图,正方形ABCD内接于☉O,P为上一点,连接DP,CP.
(1)∠CPD= °.
(2)若DC=4,CP=2,求DP的长.
【练素养】
12.(1)如图1,△ABC是☉O的内接正三角形,P为劣弧BC上一动点,求证:PA=PB+PC.
(2)如图2,四边形ABCD是☉O的内接正方形,P为劣弧BC上一动点,求证:PA=PC+PB.
(3)如图3,六边形ABCDEF是☉O的内接正六边形,P为劣弧BC上一动点,直接写出PA,PB,PC三者之间的数量关系.
参考答案
练基础
1.B 2.C
3.【解析】如图1,△BCD即圆的内接正三角形.
如图2,八边形AECHBFDG即圆的内接正八边形.
4.A 5.B
练能力
6.D 7.A 8.2a2
9.【解析】(1)
如图,AB为☉O的内接正六边形的一边,连接OA,OB,过点O作OM⊥AB于点M.
∵六边形ABCDEF为正六边形,
∴OA=OB,中心角∠AOB=×360°=60°,
∴△OAB为等边三角形,
∴半径OA=AB=4.
∵边心距OM⊥AB,
∴∠AOM=∠BOM=30°,AM=AB=2,
∴边心距OM=AM=2.
(2)正六边形的外接圆的周长=2π×OA=8π;
外接圆的面积=π×42=16π.
10.【解析】如图,延长AB,一定交正六边形于格点E,连接CE.
正六边形的边长为1,则其半径是1,则CE=4.
中间间隔一个顶点的两个顶点之间的距离是,
则△BCE的边EC上的高是,
△ACE的边EC上的高是,
则S△ABC=S△AEC-S△BEC=×4×=2.
11.【解析】(1)如图,连接BD.
∵正方形ABCD内接于☉O,P为上一点,
∴∠DBC=45°.∵∠CPD=∠DBC,∴∠CPD=45°,故答案为45.
(2)如图,作CH⊥DP于点H.∵CP=2,∠CPD=45°,∴CH=PH=2.∵DC=4,∴DH==2,∴DP=PH+DH=2+2.
练素养
12.【解析】(1)证明:如图1,连接BP并延长至E,使PE=PC,连接CE.
∵四边形ABPC是☉O的内接四边形,
∴∠BAC+∠BPC=180°.
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°.
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP.
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC.
在△BEC和△APC中,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)证明:如图2,连接BP,过点B作BE⊥PB交PA于点E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,
∴PE=PB.
在△ABE和△CBP中,
∴△ABE≌△CBP(SAS),
∴PC=AE,∴PA=AE+PE=PC+PB.
(3)PA=PC+PB.
提示:如图3,连接PC,过点B作BM⊥AP,在AP上截取AQ=PC,连接BQ.
∵∠BAP=∠BCP,AB=BC,
在△ABQ和△CBP中,
∴△ABQ≌△CBP(SAS),
∴BQ=BP,
∴MP=QM.
又∵∠APB=30°,
∴PM=PB,
∴PQ=PB,
∴PA=PQ+AQ=PC+PB.
2
