2023-2024学年初中数学冀教版九年级上册第23章 数据分析 分层作业(含答案)
文档属性
| 名称 | 2023-2024学年初中数学冀教版九年级上册第23章 数据分析 分层作业(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 393.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 18:33:42 | ||
图片预览



文档简介
第二十三章 数据分析 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共30分)
1.如果一组数据3,7,2,a,4,6的平均数是5,那么a的值是 ( )
A.8 B.5 C.4 D.3
2.已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数是 ( )
A.5 B.5.5 C.6 D.6.5
3.【遵化期中】在方差的计算公式s2=[(x1-20)2+(x2-20)2+…+(x10-20)2]中,数字10和20分别表示的意义可以是 ( )
A.数据的个数和方差
B.平均数和数据的个数
C.数据的个数和平均数
D.数据组的方差和平均数
4.【永年区期中】甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是 ( )
A.甲 B.乙 C.丙 D.丁
5.某校举办“喜迎建团100周年”校园朗诵大赛,小丽同学根据比赛中七位评委所给的某位参赛选手的分数,制作了一个表格,若去掉一个最高分和一个最低分,则表中数据一定不发生变化的是 ( )
中位数 众数 平均数 方差
9.3 9.4 9.2 9.5
A.中位数 B.众数 C.平均数 D.方差
6.【信都区期中】在数据4,5,6,5中添加一个数据,而平均数不发生变化,则添加的数据为 ( )
A.0 B.5 C.4.5 D.5.5
7.【滦州期中】某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是 ( )
劳动时间/小时 3 3.5 4 4.5
人数 1 1 2 1
A.中位数是4,平均数是3.75
B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8
D.众数是2,平均数是3.8
8.【正定期中】在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的 ( )
A.平均数
B.众数
C.中位数
D.最高分与最低分数的差
9.【玉田期中】2022年在北京——张家口举办了冬季奥运会,北京成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名选手进行了五次测试,测试成绩如图所示,选手成绩更稳定的是 ( )
A.甲 B.乙
C.都一样 D.不能确定
10.【信都区期末】如果一组数据的方差是s2=[(x1-20)2+(x2-20)2+…+(x12-20)2],已知9是这组数据中的一个数据,现把9去掉,则所得新数据的平均数是 ( )
A.12 B.15 C.18 D.21
二、填空题(每小题3分,共9分)
11.【信都区期中】已知一组数据-1,2,0,1,-2,那么这组数据的方差是 .
12.两组数据3,a,8,5与a,6,b的平均数都是6,若将这两组数据合并为一组,则这组新数据的中位数为 .
13.【玉田期中】已知一组数据1,2,3,n,它们的平均数是2,则n= ,这组数据的方差为 .
三、解答题(共61分)
14.(9分)自由式滑雪大跳台是冬奥会的比赛项目之一,其计分规则如下:
①每次滑雪的动作,按照其完成难度的不同对应一个难度系数A;
②每次滑雪都有7名裁判进行打分,在7个得分中去掉1个最高分和1个最低分,剩下5个得分的平均值为这次起跳的完成分B;
③运动员该次滑雪的最后得分C=难度系数A×完成分B×3.
在某次自由式滑雪大跳台比赛中,裁判给某运动员的打分(满分10分)表如下:
难度 系数 裁判 1 2 3 4 5 6 7
3.0 打分 10 9.5 9.3 9 9.5 9 9
(1)直接写出7名裁判打分的众数和中位数.
(2)该运动员的最后得分是多少
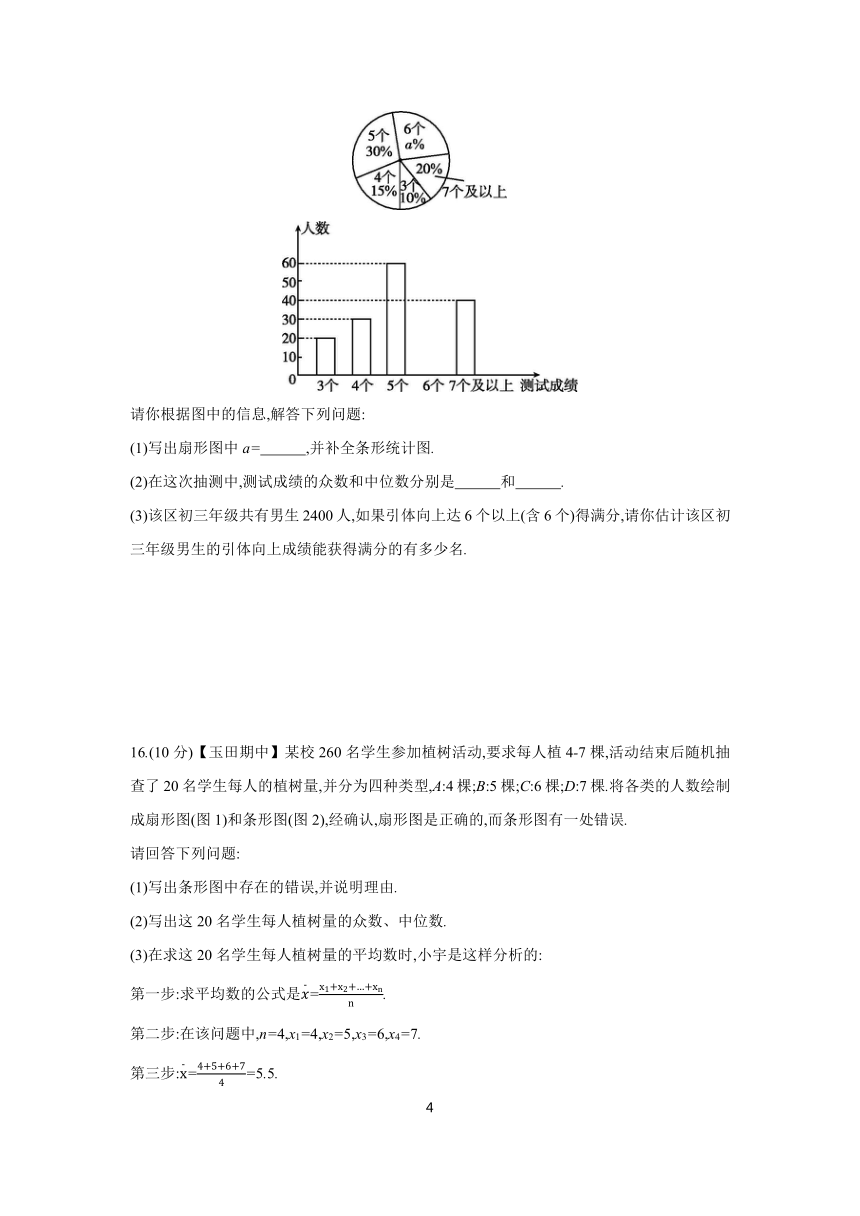
15.(10分)【桥西区期中】教育局为了了解初三男生引体向上的成绩情况,随机抽测了本区部分学校初三男生,并将测试成绩绘成了两幅不完整的统计图.
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a= ,并补全条形统计图.
(2)在这次抽测中,测试成绩的众数和中位数分别是 和 .
(3)该区初三年级共有男生2400人,如果引体向上达6个以上(含6个)得满分,请你估计该区初三年级男生的引体向上成绩能获得满分的有多少名.
16.(10分)【玉田期中】某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(图1)和条形图(图2),经确认,扇形图是正确的,而条形图有一处错误.
请回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这20名学生每人植树量的众数、中位数.
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
第一步:求平均数的公式是=.
第二步:在该问题中,n=4,x1=4,x2=5,x3=6,x4=7.
第三步:==5.5.
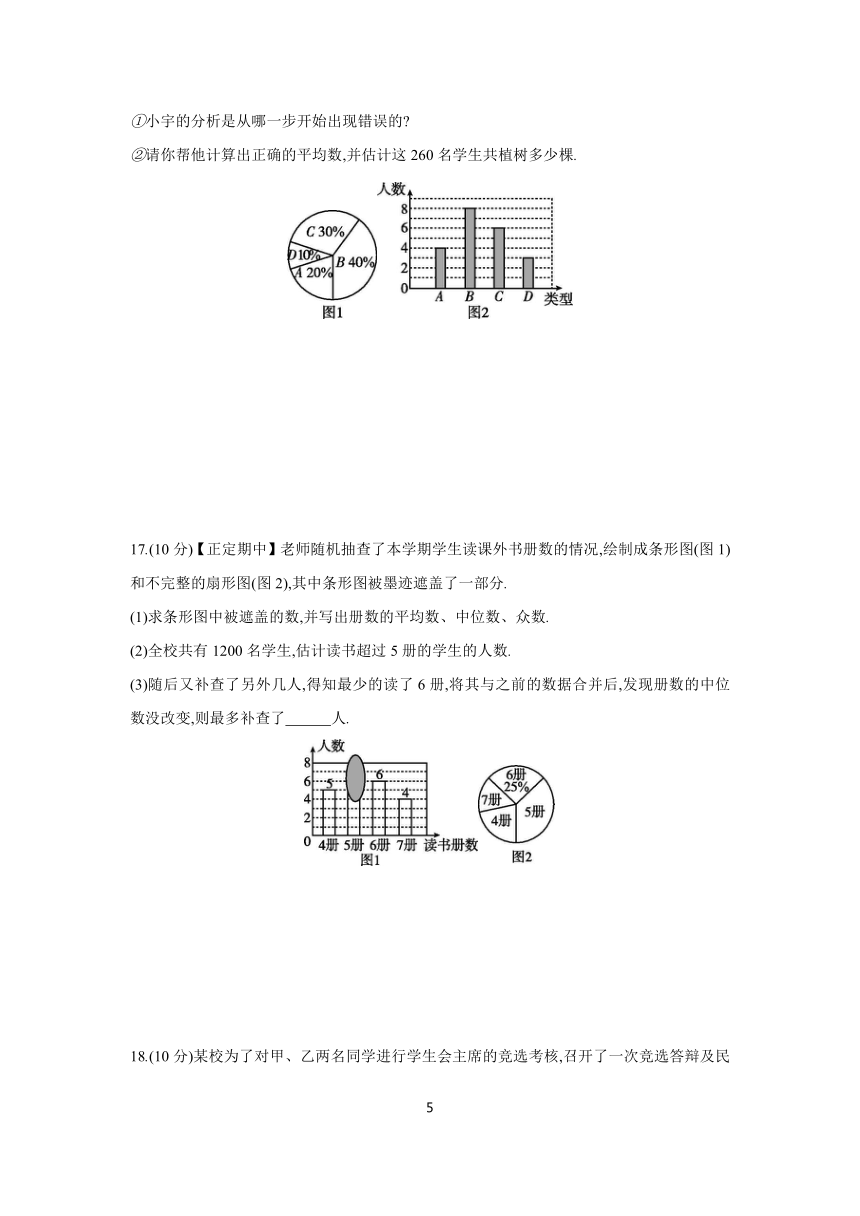
①小宇的分析是从哪一步开始出现错误的
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
17.(10分)【正定期中】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的平均数、中位数、众数.
(2)全校共有1200名学生,估计读书超过5册的学生的人数.
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.
18.(10分)某校为了对甲、乙两名同学进行学生会主席的竞选考核,召开了一次竞选答辩及民主测评会,由A,B,C,D,E五位教师评委对竞选答辩进行评分,并选出20名学生代表参加民主投票.竞选答辩的结果如下表所示:
评委得分选手 A B C D E
甲 92 88 90 94 96
乙 84 86 90 93 91
根据以上信息解答下列问题:
(1)甲、乙两人的竞选答辩得分分别是多少
(2)如果综合得分=竞选答辩得分+民主投票得分,那么甲、乙两人谁当选学生会主席
(3)如果综合得分=竞选答辩得分×a+民主投票得分×(1-a),那么当a=0.6时,甲、乙两人谁当选学生会主席
19.(12分)【滦州期中】某数学课外小组开展数学闯关游戏(游戏一共10关),根据活动结果制成两幅尚不完整的统计图.
(1)求a的值.
(2)计算闯9关的人数并补全条形统计图.
(3)求数学课外活动小组的平均闯关关数.
(4)再加入n名同学闯关,已知这n名同学的闯关关数均大于7,若加入后闯关关数的中位数与原闯关关数的中位数相等,则n最多是 .
参考答案
1.A 2.B 3.C 4.C 5.A 6.B 7.C 8.C 9.A
10.D
11.2 12.6 13.2
14.【解析】(1)众数是9,中位数是9.3.
(2)3.0××(9.5+9.5+9.3+9+9)×3=83.34(分).
答:该运动员的最后得分是83.34分.
15.【解析】(1)25.
补全条形统计图如图所示.
(2)5;5.
(3)×2400=1080(名).
答:估计该区初三年级男生的引体向上成绩能获得满分的有1080名.
16.【解析】(1)D错误,理由:20×10%=2≠3.
(2)众数为5,中位数为5.
(3)①第二步;
②==5.3,
估计这260名学生共植树5.3×260=1378(棵).
17.【解析】(1)∵被抽查的总人数为6÷25%=24(人),
∴读书5册的人数为24-(5+6+4)=9(人),
平均数为(4×5+5×9+6×6+4×7)÷24=,
被抽查的学生读书册数的中位数是第12,13个数据的平均数,而第12,13个数据均为5,
∴被抽查的学生读书册数的中位数为5,众数为5.
答:条形图中被遮盖的数是9,册数的平均数是,中位数是5,众数是5.
(2)1200×=500(人).
答:全校读书超过5册的学生人数约为500.
(3)∵4册和5册的人数和为14,中位数没有改变,
∴总人数不能超过27,即最多补查了3人.
故答案为3.
18.【解析】(1)甲的竞选答辩得分为=92(分),
乙的竞选答辩得分为=89(分).
(2)甲的综合得分=92+8=100(分),
乙的综合得分=89+12=101(分).
∵100<101,
∴乙当选学生会主席.
(3)当a=0.6时,甲的综合得分=92×0.6+8×0.4=58.4(分),
乙的综合得分=89×0.6+12×0.4=58.2(分).
∵58.4>58.2,
∴甲当选学生会主席.
19.【解析】(1)a%=1-(10%+25%+30%+20%)=15%,即a=15.
(2)因为总人数为2÷10%=20,
所以闯9关的人数为20-(2+5+6+3)=4,
补全条形统计图如下.
(3)数学课外活动小组的平均闯关关数为=7.1.
(4)原数据的中位数为第10,11个数据的平均数,即中位数为=7,
若加入后闯关关数的中位数与原闯关关数的中位数相等,则n最多是5.
故答案为5.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共30分)
1.如果一组数据3,7,2,a,4,6的平均数是5,那么a的值是 ( )
A.8 B.5 C.4 D.3
2.已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数是 ( )
A.5 B.5.5 C.6 D.6.5
3.【遵化期中】在方差的计算公式s2=[(x1-20)2+(x2-20)2+…+(x10-20)2]中,数字10和20分别表示的意义可以是 ( )
A.数据的个数和方差
B.平均数和数据的个数
C.数据的个数和平均数
D.数据组的方差和平均数
4.【永年区期中】甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是 ( )
A.甲 B.乙 C.丙 D.丁
5.某校举办“喜迎建团100周年”校园朗诵大赛,小丽同学根据比赛中七位评委所给的某位参赛选手的分数,制作了一个表格,若去掉一个最高分和一个最低分,则表中数据一定不发生变化的是 ( )
中位数 众数 平均数 方差
9.3 9.4 9.2 9.5
A.中位数 B.众数 C.平均数 D.方差
6.【信都区期中】在数据4,5,6,5中添加一个数据,而平均数不发生变化,则添加的数据为 ( )
A.0 B.5 C.4.5 D.5.5
7.【滦州期中】某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是 ( )
劳动时间/小时 3 3.5 4 4.5
人数 1 1 2 1
A.中位数是4,平均数是3.75
B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8
D.众数是2,平均数是3.8
8.【正定期中】在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的 ( )
A.平均数
B.众数
C.中位数
D.最高分与最低分数的差
9.【玉田期中】2022年在北京——张家口举办了冬季奥运会,北京成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名选手进行了五次测试,测试成绩如图所示,选手成绩更稳定的是 ( )
A.甲 B.乙
C.都一样 D.不能确定
10.【信都区期末】如果一组数据的方差是s2=[(x1-20)2+(x2-20)2+…+(x12-20)2],已知9是这组数据中的一个数据,现把9去掉,则所得新数据的平均数是 ( )
A.12 B.15 C.18 D.21
二、填空题(每小题3分,共9分)
11.【信都区期中】已知一组数据-1,2,0,1,-2,那么这组数据的方差是 .
12.两组数据3,a,8,5与a,6,b的平均数都是6,若将这两组数据合并为一组,则这组新数据的中位数为 .
13.【玉田期中】已知一组数据1,2,3,n,它们的平均数是2,则n= ,这组数据的方差为 .
三、解答题(共61分)
14.(9分)自由式滑雪大跳台是冬奥会的比赛项目之一,其计分规则如下:
①每次滑雪的动作,按照其完成难度的不同对应一个难度系数A;
②每次滑雪都有7名裁判进行打分,在7个得分中去掉1个最高分和1个最低分,剩下5个得分的平均值为这次起跳的完成分B;
③运动员该次滑雪的最后得分C=难度系数A×完成分B×3.
在某次自由式滑雪大跳台比赛中,裁判给某运动员的打分(满分10分)表如下:
难度 系数 裁判 1 2 3 4 5 6 7
3.0 打分 10 9.5 9.3 9 9.5 9 9
(1)直接写出7名裁判打分的众数和中位数.
(2)该运动员的最后得分是多少
15.(10分)【桥西区期中】教育局为了了解初三男生引体向上的成绩情况,随机抽测了本区部分学校初三男生,并将测试成绩绘成了两幅不完整的统计图.
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a= ,并补全条形统计图.
(2)在这次抽测中,测试成绩的众数和中位数分别是 和 .
(3)该区初三年级共有男生2400人,如果引体向上达6个以上(含6个)得满分,请你估计该区初三年级男生的引体向上成绩能获得满分的有多少名.
16.(10分)【玉田期中】某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(图1)和条形图(图2),经确认,扇形图是正确的,而条形图有一处错误.
请回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这20名学生每人植树量的众数、中位数.
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
第一步:求平均数的公式是=.
第二步:在该问题中,n=4,x1=4,x2=5,x3=6,x4=7.
第三步:==5.5.
①小宇的分析是从哪一步开始出现错误的
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
17.(10分)【正定期中】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的平均数、中位数、众数.
(2)全校共有1200名学生,估计读书超过5册的学生的人数.
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.
18.(10分)某校为了对甲、乙两名同学进行学生会主席的竞选考核,召开了一次竞选答辩及民主测评会,由A,B,C,D,E五位教师评委对竞选答辩进行评分,并选出20名学生代表参加民主投票.竞选答辩的结果如下表所示:
评委得分选手 A B C D E
甲 92 88 90 94 96
乙 84 86 90 93 91
根据以上信息解答下列问题:
(1)甲、乙两人的竞选答辩得分分别是多少
(2)如果综合得分=竞选答辩得分+民主投票得分,那么甲、乙两人谁当选学生会主席
(3)如果综合得分=竞选答辩得分×a+民主投票得分×(1-a),那么当a=0.6时,甲、乙两人谁当选学生会主席
19.(12分)【滦州期中】某数学课外小组开展数学闯关游戏(游戏一共10关),根据活动结果制成两幅尚不完整的统计图.
(1)求a的值.
(2)计算闯9关的人数并补全条形统计图.
(3)求数学课外活动小组的平均闯关关数.
(4)再加入n名同学闯关,已知这n名同学的闯关关数均大于7,若加入后闯关关数的中位数与原闯关关数的中位数相等,则n最多是 .
参考答案
1.A 2.B 3.C 4.C 5.A 6.B 7.C 8.C 9.A
10.D
11.2 12.6 13.2
14.【解析】(1)众数是9,中位数是9.3.
(2)3.0××(9.5+9.5+9.3+9+9)×3=83.34(分).
答:该运动员的最后得分是83.34分.
15.【解析】(1)25.
补全条形统计图如图所示.
(2)5;5.
(3)×2400=1080(名).
答:估计该区初三年级男生的引体向上成绩能获得满分的有1080名.
16.【解析】(1)D错误,理由:20×10%=2≠3.
(2)众数为5,中位数为5.
(3)①第二步;
②==5.3,
估计这260名学生共植树5.3×260=1378(棵).
17.【解析】(1)∵被抽查的总人数为6÷25%=24(人),
∴读书5册的人数为24-(5+6+4)=9(人),
平均数为(4×5+5×9+6×6+4×7)÷24=,
被抽查的学生读书册数的中位数是第12,13个数据的平均数,而第12,13个数据均为5,
∴被抽查的学生读书册数的中位数为5,众数为5.
答:条形图中被遮盖的数是9,册数的平均数是,中位数是5,众数是5.
(2)1200×=500(人).
答:全校读书超过5册的学生人数约为500.
(3)∵4册和5册的人数和为14,中位数没有改变,
∴总人数不能超过27,即最多补查了3人.
故答案为3.
18.【解析】(1)甲的竞选答辩得分为=92(分),
乙的竞选答辩得分为=89(分).
(2)甲的综合得分=92+8=100(分),
乙的综合得分=89+12=101(分).
∵100<101,
∴乙当选学生会主席.
(3)当a=0.6时,甲的综合得分=92×0.6+8×0.4=58.4(分),
乙的综合得分=89×0.6+12×0.4=58.2(分).
∵58.4>58.2,
∴甲当选学生会主席.
19.【解析】(1)a%=1-(10%+25%+30%+20%)=15%,即a=15.
(2)因为总人数为2÷10%=20,
所以闯9关的人数为20-(2+5+6+3)=4,
补全条形统计图如下.
(3)数学课外活动小组的平均闯关关数为=7.1.
(4)原数据的中位数为第10,11个数据的平均数,即中位数为=7,
若加入后闯关关数的中位数与原闯关关数的中位数相等,则n最多是5.
故答案为5.
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
