2023-2024学年初中数学冀教版九年级上册第25章 图形的相似 分层作业(含解析)
文档属性
| 名称 | 2023-2024学年初中数学冀教版九年级上册第25章 图形的相似 分层作业(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览




文档简介
第二十五章 图形的相似 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共36分)
1.观察下列图形,是相似图形的是 ( )
A. B.
C. D.
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,
同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是 ( )
A. B.1 C. D.2
3.如图,在△ABC中,DE∥BC,=,则下列结论中正确的是 ( )
A.=
B.=
C.=
D.=
4.如图,在方格纸上,以点O为位似中心,把△ABC缩小到原来的,则点A的对应点为 ( )
A.点D B.点E
C.点D或点F D.点D或点G
5.【高邑期中】如图,△ABC∽△DEF,则∠D的度数为 ( )
A.35° B.45°
C.65° D.80°
6.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3,4,5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是 ( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
7.如图,△ABC和△A'B'C'是位似图形,位似中心是点O,则下列说法不正确的是 ( )
A.AA'∥BB'
B.直线CC'经过点O
C.直线AA',BB'和CC'相交于一点
D.AB∥A'B'
8.神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618.这体现了数学中的 ( )
A.平移 B.旋转
C.轴对称 D.黄金分割
9.如图,a∥b∥c∥d∥e,每相邻两条直线之间的距离均相等.点A,B,C分别在直线a,e,c上,AC交b于点D,BC交d于点G,AB分别交c,d于点E,F.若四边形DEFG的面积为4,则△ABC的面积为 ( )
A.8 B. C. D.12
10.【石家庄期中】有一块锐角三角形余料△ABC,边BC为15 cm,BC边上的高为12 cm,现要把它分割成若干个邻边长分别为5 cm和2 cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为5 cm的边在BC上,则按如图所示的方式分割成的小长方形零件最多有 ( )
A.3个
B.4个
C.5个
D.6个
11.【桥西区期中】图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB= ( )
A.1 cm B.2 cm C.3 cm D.4 cm
12.对于题目:“在边长为6和2的矩形内,分别剪下两个小矩形,使得剪下的两个矩形均与原矩形相似,请设计剪下的两个矩形周长和为最大值时的方案,并求出这个最大值.”甲、乙两个同学设计了自认为满足条件的方案,并求出了周长和的最大值.甲方案:如图1,最大值为16,乙方案:如图2,最大值为16.下列选项中说法正确的是 ( )
A.甲方案正确,周长和的最大值错误
B.乙方案错误,周长和的最大值正确
C.甲、乙方案均正确,周长和的最大值正确
D.甲、乙方案均错误,周长和的最大值错误
二、填空题(每小题3分,共9分)
13.如图,在△ABC中,点E,F分别在边AB,AC上,∠1=∠2.若BC=4,AF=2,CF=3,则EF= .
14.如图,用几个相同的含30°角的直角三角板按照如图所示的方式拼成一个封闭的多边形,中间围成的图形是正 边形,中间围成的图形和较长直角边围成的图形面积之比是 .
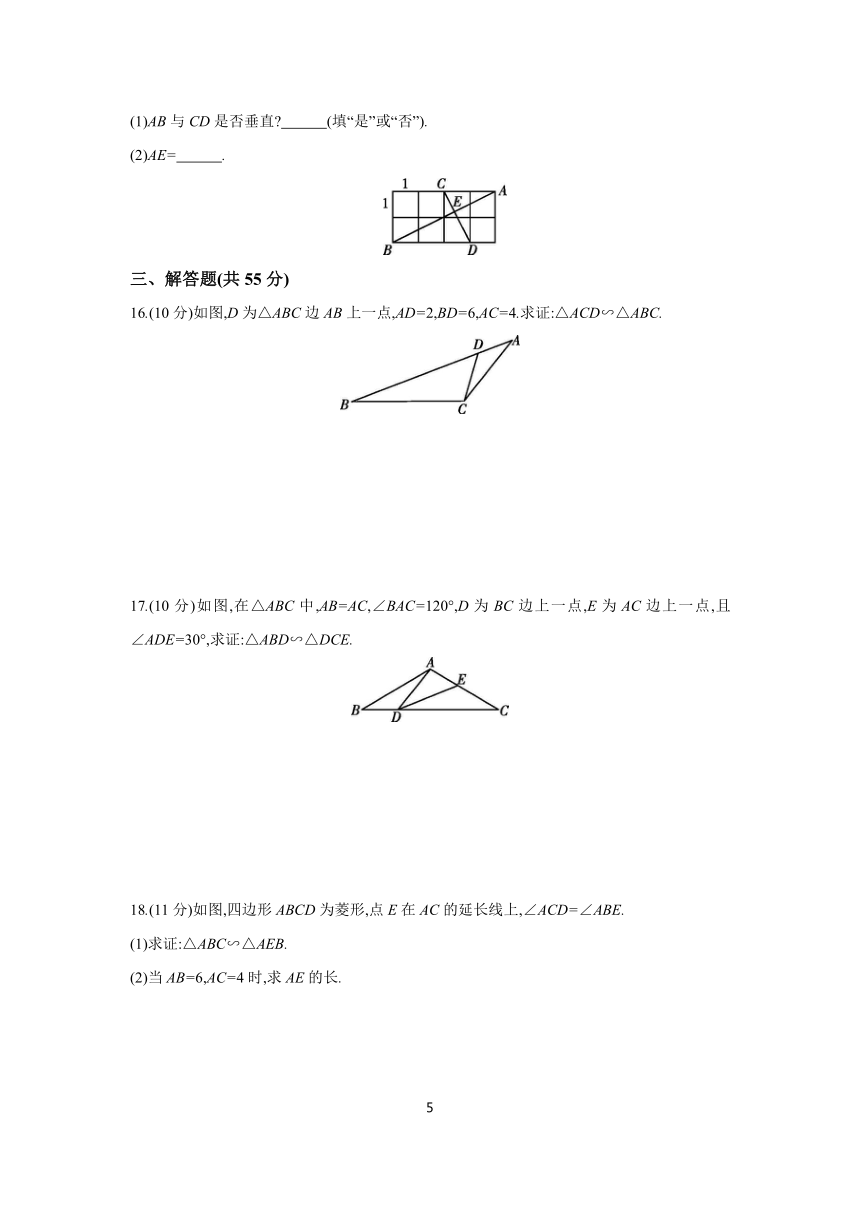
15.如图,这是钉板示意图,每相邻4个钉点是边长为1个单位长度的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E.
(1)AB与CD是否垂直 (填“是”或“否”).
(2)AE= .
三、解答题(共55分)
16.(10分)如图,D为△ABC边AB上一点,AD=2,BD=6,AC=4.求证:△ACD∽△ABC.
17.(10分)如图,在△ABC中,AB=AC,∠BAC=120°,D为BC边上一点,E为AC边上一点,且∠ADE=30°,求证:△ABD∽△DCE.
18.(11分)如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB.
(2)当AB=6,AC=4时,求AE的长.
19.(12分)【永年区期中】如图,在菱形ABCD中,点E,F分别在边AB,AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)求证:△BEC∽△BCH.
(2)如果BE2=AB·AE,求证:AG=DF.
20.(12分)定义:若一个三角形一边长的平方等于另两边长的乘积的2倍,我们把这个三角形叫做“有趣三角形”.
(1)若△ABC是“有趣三角形”,AB=3,BC=6,则AC= .
(2)已知等腰△ABC的周长为10,若△ABC是“有趣三角形”,求△ABC的腰长.
(3)如图,在△ABC中,∠ACB=135°,点D,E在边AB上,且△CDE是以DE为斜边的等腰直角三角形.求证:由三条线段AD,DE,BE组成的三角形是“有趣三角形”.
参考答案
1.C
2.C 【解析】如图,过点A作平行横线的垂线,交点B所在的平行横线于点D,交点C所在的平行横线于点E,则=,即=2,解得BC=,故选C.
3.C 【解析】∵DE∥BC,∴△ADE∽△ABC,∴===,故A,B错误,
∴=,故C正确,
∴=2=.故D错误.故选C.
4.D
5.C 【解析】∵△ABC∽△DEF,
∴∠B=∠E=35°,∠C=∠F=80°,
∴∠D=180°-35°-80°=65°.
故选C.
6.A
7.A 【解析】∵△ABC和△A'B'C'是位似图形,位似中心是点O,∴直线AA',BB'和CC'相交于点O,AB∥A'B',故选A.
8.D 【解析】∵每圈螺纹的直径与相邻螺纹直径的比约为0.618,又∵黄金分割比为≈0.618,∴其每圈螺纹的直径与相邻螺纹直径的比约为0.618,这体现了数学中的黄金分割,故选D.
9.C 【解析】由图像可得D,E,F,G分别为AC,AB,EB,BC的中点,
∴DG,DE,FG分别为△CAB,△ABC,△BEC的中位线,
∴S△CDG=S△AED=S△ABC,S△BFG=S△BEC=S△ABC.
∵四边形DEFG的面积为4,
∴S△ABC-S△CDG-S△AED-S△BFG=S△ABC=4,
∴S△ABC=.
故选C.
10.D 【解析】如图,当最上层的小长方形的一边与AB,AC交于点E,F时,EF∥BC,作AD⊥BC交EF于点G,交BC于点D,∴△AEF∽△ABC,∴=.
∵BC=15 cm,AD=12 cm,小长方形邻边长分别为5 cm 和2 cm,
∴=,
解得AG=4,
∴GD=8 cm.
∵小长方形的宽为2 cm,
∴能分割4层小长方形.
∵BC=15 cm,
∴最底层能裁2个小长方形.
设倒数第二层的小长方形的上底面所在直线与AB,AC分别交于点M,N,与AD交于点H,AH=8,∴△AEF∽△AMN,∴==,∴MN=10,恰好能裁2个小长方形,
故最多有1+1+2+2=6个小长方形.
故选D.
11.C 【解析】如图,过点O作OM⊥CD,垂足为M,过点O'作O'N⊥AB,垂足为N.
∵CD∥AB,
∴△CDO∽△ABO',即相似比为,
∴=.
∵OM=15-7=8(cm),O'N=11-7=4(cm),
∴=,
∴AB=3 cm,
故选C.
12.C 【解析】如题图1,由题意可以假设两个矩形的宽、长分别为x,3x;y,3y,
则有3x+3y=6,
∴x+y=2,
∴两个矩形的周长的和为8x+8y=16,
∴甲的方案正确,周长和的最大值正确.
如题图2,由题意可以假设两个矩形的宽、长分别为m,3m;n,3n,
则有m+n=2,
∴两个矩形的周长的和为8m+8n=16,
∴乙的方案正确,周长和的最大值正确.
故选C.
13. 【解析】∵∠1=∠2,∠A=∠A,
∴△AEF∽△ABC,
∴=.
∵BC=4,AF=2,CF=3,
∴=,
∴EF=.
故答案为.
14.六 1∶3或 【解析】如图.
∵∠EAC=30°+90°=120°,三角板的摆法相同,
∴外周的封闭图形为正六边形,边长AE=DE.
∵∠ABC=60°,
∴∠DBC=120°,
∴中间围成的图形也是正六边形.
∵边长AD=2DE,AB=DE,
∴DB=AD-AB=DE,
∴==.
∵内部和外周的正六边形为相似图形,
∴相似比为,
∴面积比为2,即.
15.(1)是 (2) 【解析】(1)如图1,作出M,F2个钉点.
在△ACM和△CFD中,
∴△ACM≌△CFD(SAS),
∴∠CAM=∠FCD.
∵∠CAM+∠CMA=90°,
∴∠FCD+∠CMA=90°,
∴∠CEM=90°,
∴AB⊥CD.
(2)如图2,作出钉点H.
在Rt△ABH中,AB===2.
∵AC∥BD,
∴∠CAE=∠DBE,∠ACE=∠BDE,
∴△ACE∽△BDE,
∴==,
∴=,
∴AE=.
故答案为.
16.【解析】证明:∵AD=2,BD=6,
∴AB=8,
∴==,==,
∴=.
又∵∠A=∠A,
∴△ACD∽△ABC.
17.【解析】证明:∵AB=AC,且∠BAC=120°,
∴∠ABD=∠ACB=30°.
∵∠ADE=30°,
∴∠ABD=∠ADE=30°.
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE.
18.【解析】(1)证明:∵四边形ABCD为菱形,
∴∠ACD=∠BCA.
∵∠ACD=∠ABE,
∴∠BCA=∠ABE.
∵∠BAC=∠EAB,
∴△ABC∽△AEB.
(2)∵△ABC∽△AEB,
∴=.
∵AB=6,AC=4,
∴=,
∴AE==9.
19.【解析】证明:(1)∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B.
∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE.
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE.
∵∠B=∠B,
∴△BEC∽△BCH.
(2)∵BE2=AB·AE,
∴=.
∵CB∥DG,
∴=,
∴=.
∵BC=AB,
∴AG=BE.
∵△CDF≌△CBE,
∴DF=BE,
∴AG=DF.
20.【解析】(1)①由题意可知,BC2=62=36,2AB·AC=6AC.
∵△ABC是“有趣三角形”,
∴BC2=2AB·AC,
∴36=6AC,∴AC=6.
②由题意可知,AB2=32=9,2BC·AC=12AC.
∵△ABC是“有趣三角形”,
∴AB2=2BC·AC,
∴9=12AC,
∴AC=.
∵3+<6,
∴AC=不符合题意,舍去.
③由题意可知,2AB·BC=36,
∵△ABC是“有趣三角形”,
∴AC2=2AB·BC,
∴AC2=36,∴AC=6(负值舍去),
综上所述,AC=6.
故答案为6.
(2)设等腰三角形的腰长为x,则底边长为10-2x,
①根据题意可知,x2=2x(10-2x),
解得x=0(舍去)或x=4.
②∵2x>10-2x,
∴x>,
由题意可知,(10-2x)2=2x2,
解得x=10-5或x=10+5(舍去),
∴△ABC的腰长为4或10-5.
(3)证明:∵△CDE是以DE为斜边的等腰直角三角形,
∴∠DCE=90°,∠CED=∠CDE=45°,
∴∠A+∠ACD=45°.
∵∠ACB=135°,
∴∠A+∠B=45°,
∴∠ACD=∠B.
∵∠CDE=∠DEC=45°,
∴CD=CE,∠ADC=∠CEB=135°,
∴△ADC∽△CEB,
∴=.
在Rt△CDE中,CD=CE,
∴DE2=2CD2,
∴CD·CE=AD·BE,
∴CD2=AD·BE,
∴DE2=2AD·BE,
∴线段AD,DE,BE组成的三角形是“有趣三角形”.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共36分)
1.观察下列图形,是相似图形的是 ( )
A. B.
C. D.
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,
同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是 ( )
A. B.1 C. D.2
3.如图,在△ABC中,DE∥BC,=,则下列结论中正确的是 ( )
A.=
B.=
C.=
D.=
4.如图,在方格纸上,以点O为位似中心,把△ABC缩小到原来的,则点A的对应点为 ( )
A.点D B.点E
C.点D或点F D.点D或点G
5.【高邑期中】如图,△ABC∽△DEF,则∠D的度数为 ( )
A.35° B.45°
C.65° D.80°
6.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3,4,5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是 ( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
7.如图,△ABC和△A'B'C'是位似图形,位似中心是点O,则下列说法不正确的是 ( )
A.AA'∥BB'
B.直线CC'经过点O
C.直线AA',BB'和CC'相交于一点
D.AB∥A'B'
8.神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618.这体现了数学中的 ( )
A.平移 B.旋转
C.轴对称 D.黄金分割
9.如图,a∥b∥c∥d∥e,每相邻两条直线之间的距离均相等.点A,B,C分别在直线a,e,c上,AC交b于点D,BC交d于点G,AB分别交c,d于点E,F.若四边形DEFG的面积为4,则△ABC的面积为 ( )
A.8 B. C. D.12
10.【石家庄期中】有一块锐角三角形余料△ABC,边BC为15 cm,BC边上的高为12 cm,现要把它分割成若干个邻边长分别为5 cm和2 cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为5 cm的边在BC上,则按如图所示的方式分割成的小长方形零件最多有 ( )
A.3个
B.4个
C.5个
D.6个
11.【桥西区期中】图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB= ( )
A.1 cm B.2 cm C.3 cm D.4 cm
12.对于题目:“在边长为6和2的矩形内,分别剪下两个小矩形,使得剪下的两个矩形均与原矩形相似,请设计剪下的两个矩形周长和为最大值时的方案,并求出这个最大值.”甲、乙两个同学设计了自认为满足条件的方案,并求出了周长和的最大值.甲方案:如图1,最大值为16,乙方案:如图2,最大值为16.下列选项中说法正确的是 ( )
A.甲方案正确,周长和的最大值错误
B.乙方案错误,周长和的最大值正确
C.甲、乙方案均正确,周长和的最大值正确
D.甲、乙方案均错误,周长和的最大值错误
二、填空题(每小题3分,共9分)
13.如图,在△ABC中,点E,F分别在边AB,AC上,∠1=∠2.若BC=4,AF=2,CF=3,则EF= .
14.如图,用几个相同的含30°角的直角三角板按照如图所示的方式拼成一个封闭的多边形,中间围成的图形是正 边形,中间围成的图形和较长直角边围成的图形面积之比是 .
15.如图,这是钉板示意图,每相邻4个钉点是边长为1个单位长度的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E.
(1)AB与CD是否垂直 (填“是”或“否”).
(2)AE= .
三、解答题(共55分)
16.(10分)如图,D为△ABC边AB上一点,AD=2,BD=6,AC=4.求证:△ACD∽△ABC.
17.(10分)如图,在△ABC中,AB=AC,∠BAC=120°,D为BC边上一点,E为AC边上一点,且∠ADE=30°,求证:△ABD∽△DCE.
18.(11分)如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB.
(2)当AB=6,AC=4时,求AE的长.
19.(12分)【永年区期中】如图,在菱形ABCD中,点E,F分别在边AB,AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)求证:△BEC∽△BCH.
(2)如果BE2=AB·AE,求证:AG=DF.
20.(12分)定义:若一个三角形一边长的平方等于另两边长的乘积的2倍,我们把这个三角形叫做“有趣三角形”.
(1)若△ABC是“有趣三角形”,AB=3,BC=6,则AC= .
(2)已知等腰△ABC的周长为10,若△ABC是“有趣三角形”,求△ABC的腰长.
(3)如图,在△ABC中,∠ACB=135°,点D,E在边AB上,且△CDE是以DE为斜边的等腰直角三角形.求证:由三条线段AD,DE,BE组成的三角形是“有趣三角形”.
参考答案
1.C
2.C 【解析】如图,过点A作平行横线的垂线,交点B所在的平行横线于点D,交点C所在的平行横线于点E,则=,即=2,解得BC=,故选C.
3.C 【解析】∵DE∥BC,∴△ADE∽△ABC,∴===,故A,B错误,
∴=,故C正确,
∴=2=.故D错误.故选C.
4.D
5.C 【解析】∵△ABC∽△DEF,
∴∠B=∠E=35°,∠C=∠F=80°,
∴∠D=180°-35°-80°=65°.
故选C.
6.A
7.A 【解析】∵△ABC和△A'B'C'是位似图形,位似中心是点O,∴直线AA',BB'和CC'相交于点O,AB∥A'B',故选A.
8.D 【解析】∵每圈螺纹的直径与相邻螺纹直径的比约为0.618,又∵黄金分割比为≈0.618,∴其每圈螺纹的直径与相邻螺纹直径的比约为0.618,这体现了数学中的黄金分割,故选D.
9.C 【解析】由图像可得D,E,F,G分别为AC,AB,EB,BC的中点,
∴DG,DE,FG分别为△CAB,△ABC,△BEC的中位线,
∴S△CDG=S△AED=S△ABC,S△BFG=S△BEC=S△ABC.
∵四边形DEFG的面积为4,
∴S△ABC-S△CDG-S△AED-S△BFG=S△ABC=4,
∴S△ABC=.
故选C.
10.D 【解析】如图,当最上层的小长方形的一边与AB,AC交于点E,F时,EF∥BC,作AD⊥BC交EF于点G,交BC于点D,∴△AEF∽△ABC,∴=.
∵BC=15 cm,AD=12 cm,小长方形邻边长分别为5 cm 和2 cm,
∴=,
解得AG=4,
∴GD=8 cm.
∵小长方形的宽为2 cm,
∴能分割4层小长方形.
∵BC=15 cm,
∴最底层能裁2个小长方形.
设倒数第二层的小长方形的上底面所在直线与AB,AC分别交于点M,N,与AD交于点H,AH=8,∴△AEF∽△AMN,∴==,∴MN=10,恰好能裁2个小长方形,
故最多有1+1+2+2=6个小长方形.
故选D.
11.C 【解析】如图,过点O作OM⊥CD,垂足为M,过点O'作O'N⊥AB,垂足为N.
∵CD∥AB,
∴△CDO∽△ABO',即相似比为,
∴=.
∵OM=15-7=8(cm),O'N=11-7=4(cm),
∴=,
∴AB=3 cm,
故选C.
12.C 【解析】如题图1,由题意可以假设两个矩形的宽、长分别为x,3x;y,3y,
则有3x+3y=6,
∴x+y=2,
∴两个矩形的周长的和为8x+8y=16,
∴甲的方案正确,周长和的最大值正确.
如题图2,由题意可以假设两个矩形的宽、长分别为m,3m;n,3n,
则有m+n=2,
∴两个矩形的周长的和为8m+8n=16,
∴乙的方案正确,周长和的最大值正确.
故选C.
13. 【解析】∵∠1=∠2,∠A=∠A,
∴△AEF∽△ABC,
∴=.
∵BC=4,AF=2,CF=3,
∴=,
∴EF=.
故答案为.
14.六 1∶3或 【解析】如图.
∵∠EAC=30°+90°=120°,三角板的摆法相同,
∴外周的封闭图形为正六边形,边长AE=DE.
∵∠ABC=60°,
∴∠DBC=120°,
∴中间围成的图形也是正六边形.
∵边长AD=2DE,AB=DE,
∴DB=AD-AB=DE,
∴==.
∵内部和外周的正六边形为相似图形,
∴相似比为,
∴面积比为2,即.
15.(1)是 (2) 【解析】(1)如图1,作出M,F2个钉点.
在△ACM和△CFD中,
∴△ACM≌△CFD(SAS),
∴∠CAM=∠FCD.
∵∠CAM+∠CMA=90°,
∴∠FCD+∠CMA=90°,
∴∠CEM=90°,
∴AB⊥CD.
(2)如图2,作出钉点H.
在Rt△ABH中,AB===2.
∵AC∥BD,
∴∠CAE=∠DBE,∠ACE=∠BDE,
∴△ACE∽△BDE,
∴==,
∴=,
∴AE=.
故答案为.
16.【解析】证明:∵AD=2,BD=6,
∴AB=8,
∴==,==,
∴=.
又∵∠A=∠A,
∴△ACD∽△ABC.
17.【解析】证明:∵AB=AC,且∠BAC=120°,
∴∠ABD=∠ACB=30°.
∵∠ADE=30°,
∴∠ABD=∠ADE=30°.
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE.
18.【解析】(1)证明:∵四边形ABCD为菱形,
∴∠ACD=∠BCA.
∵∠ACD=∠ABE,
∴∠BCA=∠ABE.
∵∠BAC=∠EAB,
∴△ABC∽△AEB.
(2)∵△ABC∽△AEB,
∴=.
∵AB=6,AC=4,
∴=,
∴AE==9.
19.【解析】证明:(1)∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B.
∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE.
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE.
∵∠B=∠B,
∴△BEC∽△BCH.
(2)∵BE2=AB·AE,
∴=.
∵CB∥DG,
∴=,
∴=.
∵BC=AB,
∴AG=BE.
∵△CDF≌△CBE,
∴DF=BE,
∴AG=DF.
20.【解析】(1)①由题意可知,BC2=62=36,2AB·AC=6AC.
∵△ABC是“有趣三角形”,
∴BC2=2AB·AC,
∴36=6AC,∴AC=6.
②由题意可知,AB2=32=9,2BC·AC=12AC.
∵△ABC是“有趣三角形”,
∴AB2=2BC·AC,
∴9=12AC,
∴AC=.
∵3+<6,
∴AC=不符合题意,舍去.
③由题意可知,2AB·BC=36,
∵△ABC是“有趣三角形”,
∴AC2=2AB·BC,
∴AC2=36,∴AC=6(负值舍去),
综上所述,AC=6.
故答案为6.
(2)设等腰三角形的腰长为x,则底边长为10-2x,
①根据题意可知,x2=2x(10-2x),
解得x=0(舍去)或x=4.
②∵2x>10-2x,
∴x>,
由题意可知,(10-2x)2=2x2,
解得x=10-5或x=10+5(舍去),
∴△ABC的腰长为4或10-5.
(3)证明:∵△CDE是以DE为斜边的等腰直角三角形,
∴∠DCE=90°,∠CED=∠CDE=45°,
∴∠A+∠ACD=45°.
∵∠ACB=135°,
∴∠A+∠B=45°,
∴∠ACD=∠B.
∵∠CDE=∠DEC=45°,
∴CD=CE,∠ADC=∠CEB=135°,
∴△ADC∽△CEB,
∴=.
在Rt△CDE中,CD=CE,
∴DE2=2CD2,
∴CD·CE=AD·BE,
∴CD2=AD·BE,
∴DE2=2AD·BE,
∴线段AD,DE,BE组成的三角形是“有趣三角形”.
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
