2023-2024学年初中数学冀教版九年级上册第26章 解直角三角形 分层作业 (含解析)
文档属性
| 名称 | 2023-2024学年初中数学冀教版九年级上册第26章 解直角三角形 分层作业 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 280.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 18:35:47 | ||
图片预览





文档简介
第二十六章 解直角三角形 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共33分)
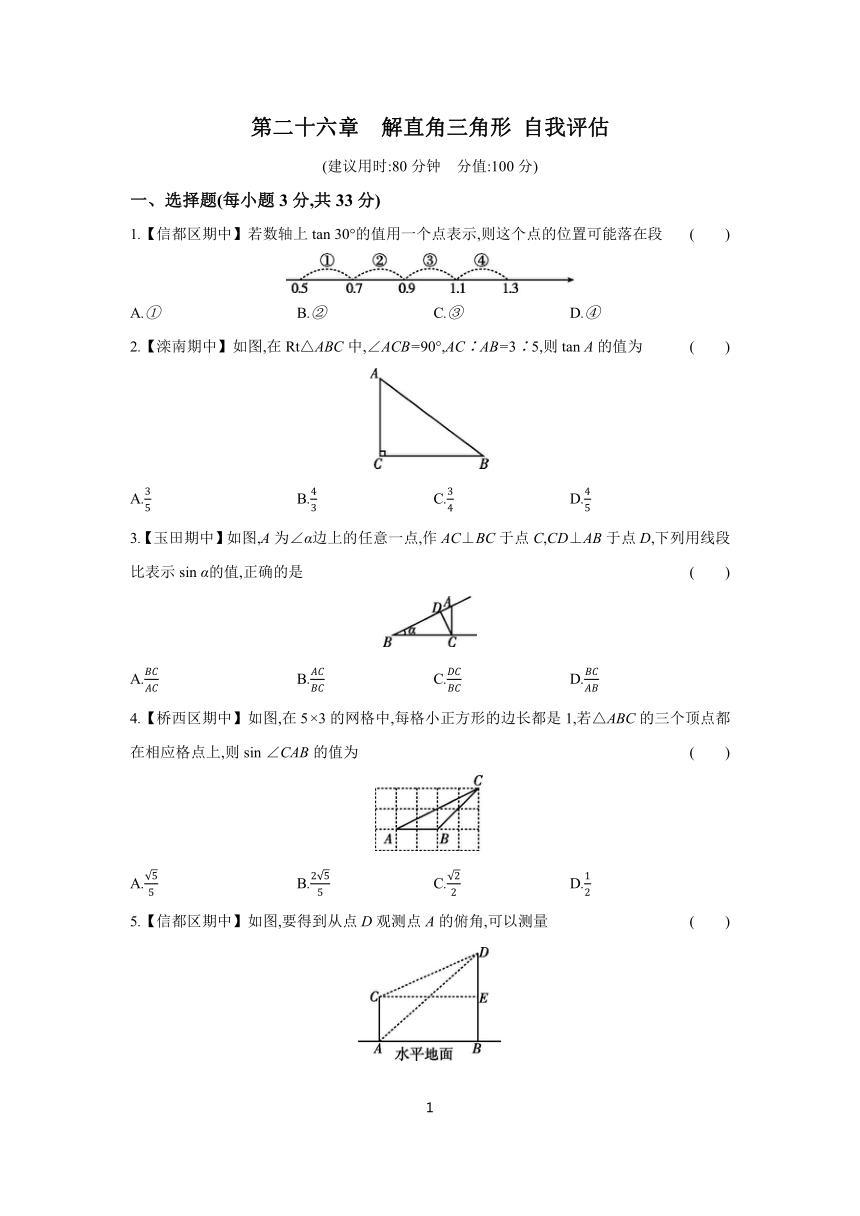
1.【信都区期中】若数轴上tan 30°的值用一个点表示,则这个点的位置可能落在段 ( )
A.① B.② C.③ D.④
2.【滦南期中】如图,在Rt△ABC中,∠ACB=90°,AC∶AB=3∶5,则tan A的值为 ( )
A. B. C. D.
3.【玉田期中】如图,A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sin α的值,正确的是 ( )
A. B. C. D.
4.【桥西区期中】如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin ∠CAB的值为 ( )
A. B. C. D.
5.【信都区期中】如图,要得到从点D观测点A的俯角,可以测量 ( )
A.∠ADC B.∠DCE
C.∠CDE D.∠DAB
6.如图,有三个小海岛A,B,C,其中海岛C到海岛A的距离为100海里,海岛B在海岛A北偏东70°的方向上,若海岛C在海岛B北偏西20°的方向上,且到海岛B的距离是50海里,则海岛C在海岛A ( )
A.北偏东20°方向 B.北偏东30°方向
C.北偏东40°方向 D.北偏西30°方向
7.【信都区期中】在平面直角坐标系中,第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,若sin α=,则点P的坐标可能是 ( )
A.(3,5)
B.(5,3)
C.(4,3)
D.(3,4)
8.【正定期中】如图,从笔直的公路l旁一点P出发,向西走6 km到达l.从P出发向北走6 km也到达l.下列说法错误的是 ( )
A.从点P向北偏西45°走3 km到达l
B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3 km后,再向西走3 km到达l
9.【玉田期中】如图,琪琪一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,且C地恰好位于A地正东方向上,则下列说法正确的是 ( )
A.B地在C地的北偏西40°方向上
B.A地在B地的南偏西60°方向上
C.∠ACB=50°
D.sin ∠BAC=
10.【永年区期中】如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为 ( )
A.1
B.2
C.
D.
11.【玉田期中】如图,小明想要测量学校操场上旗杆AB的高度,他做了如下操作:
(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为 ( )
A.a+btan α B.a+bsin α
C.a+ D.
二、填空题(每小题3分,共15分)
12.【桥西区期中】已知α为△ABC的内角,且cos(α-10°)=,则α= .
13.【永年区期中】如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则cos∠BAC的值为 .
14.【宣化区期末】如图,直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图所示的方式折叠,使点A与点B重合,折痕为DE,则tan ∠CBE的值是 .
15.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE⊥AB于点E,AE=6,cos A=.
(1)CD= .
(2)tan ∠DBC= .
16.如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,D是边AC上的动点,过点D作DE⊥AB于点E.请探究下列问题:
(1)若DE=4,则CD= .
(2)若CD=3,设F是边BC上的动点,连接FD,FE,以FD,FE为邻边作平行四边形FDGE,且使得顶点G恰好落在AC边上,则CF= .
17.(8分)【信都区期中】如图,在△ABC中,∠C=90°,AB=4,AC=.
(1)求BC.
(2)求sin A.
18.(8分)【滦州期中】如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面的夹角为60°,向高1.5米的建筑物CE引钢管AC,与水平面的夹角为30°,建筑物CE离古树的距离ED为6米,求钢管AB的长.(结果保留整数,参考数据:≈1.41,≈1.73)
19.(8分)图1是李叔叔新建的房屋,图2是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,为了测量房屋的高度,在地面上C点测得屋顶A的仰角为35°,此时地面上C点、屋檐上E点、屋顶上A点恰好三点共线,继续向房屋方向走6 m到达点D,又测得屋檐E点的仰角为60°,房屋的顶层横梁EF=12 m,EF∥CB,AB交EF于点G(点C,D,B在同一水平线上).(参考数据:sin 35°≈0.6,cos 35°≈0.8,tan 35°≈0.7,≈1.7)
(1)求屋顶到横梁的距离AG.
(2)求房屋的高AB(结果精确到1 m).
20.(8分)如图,某海岸边有B,C两个码头,C码头位于B码头的正东方向,距离B码头60海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东30°方向的C码头航行,当甲船到达距离B码头45海里的E处时,乙船位于甲船北偏东60°方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
21.(10分)【滦南期中】如图,这是在写字台上放置一个折叠式台灯时的截面示意图,已知台灯灯管DE长40 cm,灯杆CD长50 cm,台灯灯管、灯杆的夹角∠EDC=105°,灯杆CD与写字台AB的夹角∠DCB=75°.
(1)求台灯灯管DE与水平线的夹角(锐角).
(2)求灯管顶端E到写字台AB的距离,即EF的长.(台灯底座的宽度、高度都忽略不计,A,F,C,B在同一条直线上,参考数据:sin 75°≈0.97,cos 75°≈0.26,tan 75°≈3.73.结果精确到0.1 cm)
22.(10分)如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,A,B,C三点在同一水平线上.
(1)计算古树BH的高.
(2)计算教学楼CG的高(结果保留整数).(参考数据:≈1.4,≈1.7)
参考答案
1.A 2.B 3.C 4.A 5.D 6.C 7.C 8.A
9.B 【解析】如图,由题意可知,∠BAD=60°,∠CBP=50°,
∴∠BCE=∠CBP=50°,即B地在C地的北偏西50°方向上,故A错误;
∵∠ABP=60°,
∴A地在B地的南偏西60°方向上,故B正确;
∵∠ACB=90°-∠BCE=40°,故C错误;
∵∠BAD=60°,
∴∠BAC=30°,
∴sin ∠BAC=,故D错误.
故选B.
10.B 【解析】如图,过点D作DM⊥BC,交CB的延长线于点M.
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==.
∵AB=2BD,
∴===.
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k.
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选B.
11.A 12.70° 13.
14. 【解析】根据题意,BE=AE.设BE=x,则CE=8-x.
在Rt△BCE中,x2=(8-x)2+62,
解得x=,故CE=8-=,
所以tan ∠CBE==.
故答案为.
15.(1)8 (2) 【解析】(1)在Rt△ADE中,
∵AE=6,cos A==.
∴AD=10,
∴DE==8.
∵BD平分∠ABC,DE⊥AB,DC⊥CB,
∴DE=CD=8.
故答案为8.
(2)由(1)知AE=6,AD=10,CD=8,
∴AC=AD+CD=18.
在Rt△ABC中,
∵cos A==,
∴AB=30,
∴BC==24.
在Rt△DBC中,
tan ∠DBC==.
故答案为.
16.(1) (2) 【解析】(1)∵∠C=90°,AB=10,BC=6,
∴AC==8,
∴sin A=,cos A=,tan A=.
∵DE⊥AB,
∴sin A==,
∵DE=4,
∴AD=,
∴CD=AC-AD=.
故答案为.
(2)如图,四边形FDGE是平行四边形.
∵EF∥DG,
∴∠BEF=∠A,∠EFB=∠C=90°.
∵CD=3,
∴AD=5.
∵cos A==,
∴AE=4,BE=AB-AE=6.
∵sin ∠BEF=sin A=,
∴=,
∴BF=,CF=BC-BF=.
故答案为.
17.【解析】(1)∵∠C=90°,AB=4,AC=,
∴BC===3.
(2)由(1)知,BC=3.
∵∠C=90°,AB=4,
∴sin A==.
18.【解析】如图,过点C作CF⊥AD于点F,则CF=DE=6,AF=CFtan 30°=6×=2.
∴AD=AF+DF=2+1.5,
在Rt△ABD中,AB==(2+1.5)÷=4+≈6(米).
答:钢管AB的长约为6米.
19.【解析】(1)∵房屋的侧面示意图是一个轴对称图形,对称轴是房屋的高AB所在的直线,EF∥BC,
∴AG⊥EF,EG=EF=6,∠AEG=∠ACB=35°.
在Rt△AGE中,∠AGE=90°,∠AEG=35°.
∵tan ∠AEG=tan 35°=,EG=6,
∴AG≈6×0.7=4.2(米).
答:屋顶到横梁的距离AG约为4.2米.
(2)如图,过点E作EH⊥CB于点H.
设EH=x,
在Rt△EDH中,∠EHD=90°,∠EDH=60°.
∴tan ∠EDH=,
∴DH=.
在Rt△ECH中,∠EHC=90°,∠ECH=35°,
∴tan ∠ECH=,
∴CH=.
∵CH-DH=CD=6,
∴-=6,
解得x≈7.14(米),
∴AB=AG+BG≈4.2+7.14=11.34≈11(米).
答:房屋的高AB约为11米.
20.【解析】如图,分别延长BC,ED交于点F,
由题意得,∠B=90°,∠A=30°,∠BED=60°,
∴∠ADE=∠BED-∠A=30°,∠F=90°-∠BED=30°.
∵∠CDF=∠ADE=30°,
∴∠CDF=∠F,
∴CD=CF.
在Rt△BEF中,∠BEF=60°,BE=45海里,
∴BF=BE·tan 60°=45(海里),
∴CF=BF-BC=(45-60)(海里),
∴CD=(45-60)海里.
答:此时乙船与C码头之间的距离为(45-60)海里.
21.【解析】(1)如图,过点D作DH∥AB,交EF于点H,则DH⊥EF.
∵DH∥AB,
∴∠CDH=∠DCB=75°.
∵∠EDC=105°,
∴∠EDH=105°-75°=30°.
答:台灯灯管DE与水平线的夹角为30°.
(2)如图,过点D作DG⊥AB于点G,
由题意得四边形DHFG是矩形,
∴DG=HF,
在Rt△DCG中,
∵sin ∠DCG=,
∴DG=DC·sin 75°=50×0.97=48.5.
在Rt△EDH中,
∵sin ∠EDH=,
∴EH=DE·sin 30°=40×=20,
∴EF=EH+HF=20+48.5=68.5(cm).
答:灯管顶端E到写字台AB的距离是68.5 cm.
22.【解析】(1)由题意知,四边形ABED是矩形,可得DE=AB=7米,AD=BE=1.5米,
在Rt△DEH中,∵∠EDH=45°,
∴HE=DE=7米,
∴BH=EH+BE=8.5米.
(2)如图,过点H作HJ⊥CG于点J,则△HJG是等腰直角三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.
在Rt△EFG中,tan 60°=,
∴=,
∴x=(+1)≈9.45,
∴GF=7+x≈16.45,
∴CG=CF+FG≈1.5+16.45≈18(米).
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共33分)
1.【信都区期中】若数轴上tan 30°的值用一个点表示,则这个点的位置可能落在段 ( )
A.① B.② C.③ D.④
2.【滦南期中】如图,在Rt△ABC中,∠ACB=90°,AC∶AB=3∶5,则tan A的值为 ( )
A. B. C. D.
3.【玉田期中】如图,A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sin α的值,正确的是 ( )
A. B. C. D.
4.【桥西区期中】如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin ∠CAB的值为 ( )
A. B. C. D.
5.【信都区期中】如图,要得到从点D观测点A的俯角,可以测量 ( )
A.∠ADC B.∠DCE
C.∠CDE D.∠DAB
6.如图,有三个小海岛A,B,C,其中海岛C到海岛A的距离为100海里,海岛B在海岛A北偏东70°的方向上,若海岛C在海岛B北偏西20°的方向上,且到海岛B的距离是50海里,则海岛C在海岛A ( )
A.北偏东20°方向 B.北偏东30°方向
C.北偏东40°方向 D.北偏西30°方向
7.【信都区期中】在平面直角坐标系中,第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,若sin α=,则点P的坐标可能是 ( )
A.(3,5)
B.(5,3)
C.(4,3)
D.(3,4)
8.【正定期中】如图,从笔直的公路l旁一点P出发,向西走6 km到达l.从P出发向北走6 km也到达l.下列说法错误的是 ( )
A.从点P向北偏西45°走3 km到达l
B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3 km后,再向西走3 km到达l
9.【玉田期中】如图,琪琪一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,且C地恰好位于A地正东方向上,则下列说法正确的是 ( )
A.B地在C地的北偏西40°方向上
B.A地在B地的南偏西60°方向上
C.∠ACB=50°
D.sin ∠BAC=
10.【永年区期中】如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为 ( )
A.1
B.2
C.
D.
11.【玉田期中】如图,小明想要测量学校操场上旗杆AB的高度,他做了如下操作:
(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为 ( )
A.a+btan α B.a+bsin α
C.a+ D.
二、填空题(每小题3分,共15分)
12.【桥西区期中】已知α为△ABC的内角,且cos(α-10°)=,则α= .
13.【永年区期中】如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则cos∠BAC的值为 .
14.【宣化区期末】如图,直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图所示的方式折叠,使点A与点B重合,折痕为DE,则tan ∠CBE的值是 .
15.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE⊥AB于点E,AE=6,cos A=.
(1)CD= .
(2)tan ∠DBC= .
16.如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,D是边AC上的动点,过点D作DE⊥AB于点E.请探究下列问题:
(1)若DE=4,则CD= .
(2)若CD=3,设F是边BC上的动点,连接FD,FE,以FD,FE为邻边作平行四边形FDGE,且使得顶点G恰好落在AC边上,则CF= .
17.(8分)【信都区期中】如图,在△ABC中,∠C=90°,AB=4,AC=.
(1)求BC.
(2)求sin A.
18.(8分)【滦州期中】如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面的夹角为60°,向高1.5米的建筑物CE引钢管AC,与水平面的夹角为30°,建筑物CE离古树的距离ED为6米,求钢管AB的长.(结果保留整数,参考数据:≈1.41,≈1.73)
19.(8分)图1是李叔叔新建的房屋,图2是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,为了测量房屋的高度,在地面上C点测得屋顶A的仰角为35°,此时地面上C点、屋檐上E点、屋顶上A点恰好三点共线,继续向房屋方向走6 m到达点D,又测得屋檐E点的仰角为60°,房屋的顶层横梁EF=12 m,EF∥CB,AB交EF于点G(点C,D,B在同一水平线上).(参考数据:sin 35°≈0.6,cos 35°≈0.8,tan 35°≈0.7,≈1.7)
(1)求屋顶到横梁的距离AG.
(2)求房屋的高AB(结果精确到1 m).
20.(8分)如图,某海岸边有B,C两个码头,C码头位于B码头的正东方向,距离B码头60海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东30°方向的C码头航行,当甲船到达距离B码头45海里的E处时,乙船位于甲船北偏东60°方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
21.(10分)【滦南期中】如图,这是在写字台上放置一个折叠式台灯时的截面示意图,已知台灯灯管DE长40 cm,灯杆CD长50 cm,台灯灯管、灯杆的夹角∠EDC=105°,灯杆CD与写字台AB的夹角∠DCB=75°.
(1)求台灯灯管DE与水平线的夹角(锐角).
(2)求灯管顶端E到写字台AB的距离,即EF的长.(台灯底座的宽度、高度都忽略不计,A,F,C,B在同一条直线上,参考数据:sin 75°≈0.97,cos 75°≈0.26,tan 75°≈3.73.结果精确到0.1 cm)
22.(10分)如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,A,B,C三点在同一水平线上.
(1)计算古树BH的高.
(2)计算教学楼CG的高(结果保留整数).(参考数据:≈1.4,≈1.7)
参考答案
1.A 2.B 3.C 4.A 5.D 6.C 7.C 8.A
9.B 【解析】如图,由题意可知,∠BAD=60°,∠CBP=50°,
∴∠BCE=∠CBP=50°,即B地在C地的北偏西50°方向上,故A错误;
∵∠ABP=60°,
∴A地在B地的南偏西60°方向上,故B正确;
∵∠ACB=90°-∠BCE=40°,故C错误;
∵∠BAD=60°,
∴∠BAC=30°,
∴sin ∠BAC=,故D错误.
故选B.
10.B 【解析】如图,过点D作DM⊥BC,交CB的延长线于点M.
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==.
∵AB=2BD,
∴===.
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k.
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选B.
11.A 12.70° 13.
14. 【解析】根据题意,BE=AE.设BE=x,则CE=8-x.
在Rt△BCE中,x2=(8-x)2+62,
解得x=,故CE=8-=,
所以tan ∠CBE==.
故答案为.
15.(1)8 (2) 【解析】(1)在Rt△ADE中,
∵AE=6,cos A==.
∴AD=10,
∴DE==8.
∵BD平分∠ABC,DE⊥AB,DC⊥CB,
∴DE=CD=8.
故答案为8.
(2)由(1)知AE=6,AD=10,CD=8,
∴AC=AD+CD=18.
在Rt△ABC中,
∵cos A==,
∴AB=30,
∴BC==24.
在Rt△DBC中,
tan ∠DBC==.
故答案为.
16.(1) (2) 【解析】(1)∵∠C=90°,AB=10,BC=6,
∴AC==8,
∴sin A=,cos A=,tan A=.
∵DE⊥AB,
∴sin A==,
∵DE=4,
∴AD=,
∴CD=AC-AD=.
故答案为.
(2)如图,四边形FDGE是平行四边形.
∵EF∥DG,
∴∠BEF=∠A,∠EFB=∠C=90°.
∵CD=3,
∴AD=5.
∵cos A==,
∴AE=4,BE=AB-AE=6.
∵sin ∠BEF=sin A=,
∴=,
∴BF=,CF=BC-BF=.
故答案为.
17.【解析】(1)∵∠C=90°,AB=4,AC=,
∴BC===3.
(2)由(1)知,BC=3.
∵∠C=90°,AB=4,
∴sin A==.
18.【解析】如图,过点C作CF⊥AD于点F,则CF=DE=6,AF=CFtan 30°=6×=2.
∴AD=AF+DF=2+1.5,
在Rt△ABD中,AB==(2+1.5)÷=4+≈6(米).
答:钢管AB的长约为6米.
19.【解析】(1)∵房屋的侧面示意图是一个轴对称图形,对称轴是房屋的高AB所在的直线,EF∥BC,
∴AG⊥EF,EG=EF=6,∠AEG=∠ACB=35°.
在Rt△AGE中,∠AGE=90°,∠AEG=35°.
∵tan ∠AEG=tan 35°=,EG=6,
∴AG≈6×0.7=4.2(米).
答:屋顶到横梁的距离AG约为4.2米.
(2)如图,过点E作EH⊥CB于点H.
设EH=x,
在Rt△EDH中,∠EHD=90°,∠EDH=60°.
∴tan ∠EDH=,
∴DH=.
在Rt△ECH中,∠EHC=90°,∠ECH=35°,
∴tan ∠ECH=,
∴CH=.
∵CH-DH=CD=6,
∴-=6,
解得x≈7.14(米),
∴AB=AG+BG≈4.2+7.14=11.34≈11(米).
答:房屋的高AB约为11米.
20.【解析】如图,分别延长BC,ED交于点F,
由题意得,∠B=90°,∠A=30°,∠BED=60°,
∴∠ADE=∠BED-∠A=30°,∠F=90°-∠BED=30°.
∵∠CDF=∠ADE=30°,
∴∠CDF=∠F,
∴CD=CF.
在Rt△BEF中,∠BEF=60°,BE=45海里,
∴BF=BE·tan 60°=45(海里),
∴CF=BF-BC=(45-60)(海里),
∴CD=(45-60)海里.
答:此时乙船与C码头之间的距离为(45-60)海里.
21.【解析】(1)如图,过点D作DH∥AB,交EF于点H,则DH⊥EF.
∵DH∥AB,
∴∠CDH=∠DCB=75°.
∵∠EDC=105°,
∴∠EDH=105°-75°=30°.
答:台灯灯管DE与水平线的夹角为30°.
(2)如图,过点D作DG⊥AB于点G,
由题意得四边形DHFG是矩形,
∴DG=HF,
在Rt△DCG中,
∵sin ∠DCG=,
∴DG=DC·sin 75°=50×0.97=48.5.
在Rt△EDH中,
∵sin ∠EDH=,
∴EH=DE·sin 30°=40×=20,
∴EF=EH+HF=20+48.5=68.5(cm).
答:灯管顶端E到写字台AB的距离是68.5 cm.
22.【解析】(1)由题意知,四边形ABED是矩形,可得DE=AB=7米,AD=BE=1.5米,
在Rt△DEH中,∵∠EDH=45°,
∴HE=DE=7米,
∴BH=EH+BE=8.5米.
(2)如图,过点H作HJ⊥CG于点J,则△HJG是等腰直角三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.
在Rt△EFG中,tan 60°=,
∴=,
∴x=(+1)≈9.45,
∴GF=7+x≈16.45,
∴CG=CF+FG≈1.5+16.45≈18(米).
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
