第27章 反比例函数单元测试题(含答案)2023-2024学年初中数学冀教版九年级上册
文档属性
| 名称 | 第27章 反比例函数单元测试题(含答案)2023-2024学年初中数学冀教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 181.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 18:37:37 | ||
图片预览



文档简介
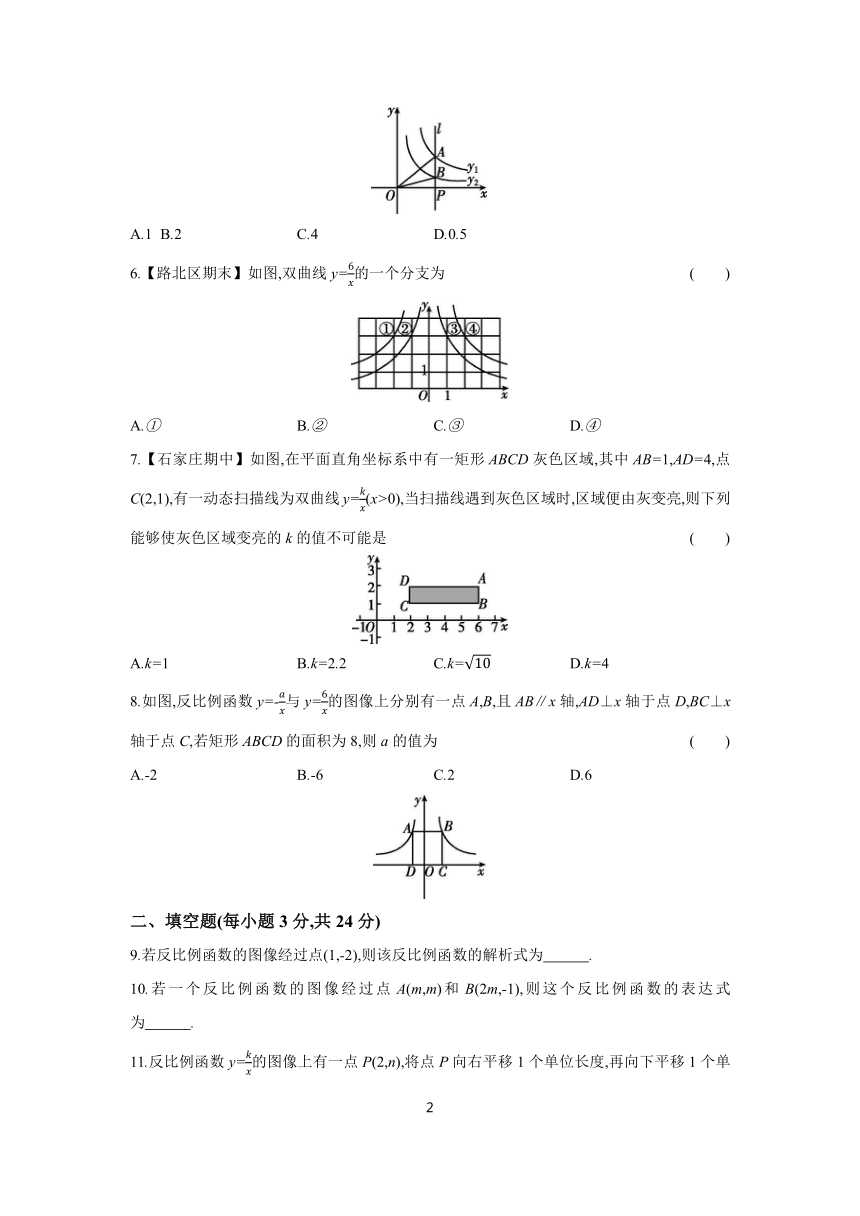
第二十七章 反比例函数 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共24分)
1.下列函数中是反比例函数的是 ( )
A.y=x+1 B.y=
C.y=-2x D.y=2x2
2.【宣化区期末】若反比例函数y=的图像经过点(-1,-2),则k的值是 ( )
A.2 B.-2 C.-3 D.3
3.已知ab<0,一次函数y=ax-b与反比例函数y=在同一直角坐标系中的图像可能是 ( )
A. B.
C. D.
4.如图,这是三个反比例函数y1=,y2=,y3=在y轴右边的图像,由此观察得到k1,k2,k3的大小关系是 ( )
A.k1>k2>k3 B.k1>k3>k2
C.k2>k3>k1 D.k3>k2>k1
5.【路北区期末】如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图像分别交于点A,B,连接OA,OB,已知k1=k2+2,则△OAB的面积是 ( )
A.1 B.2 C.4 D.0.5
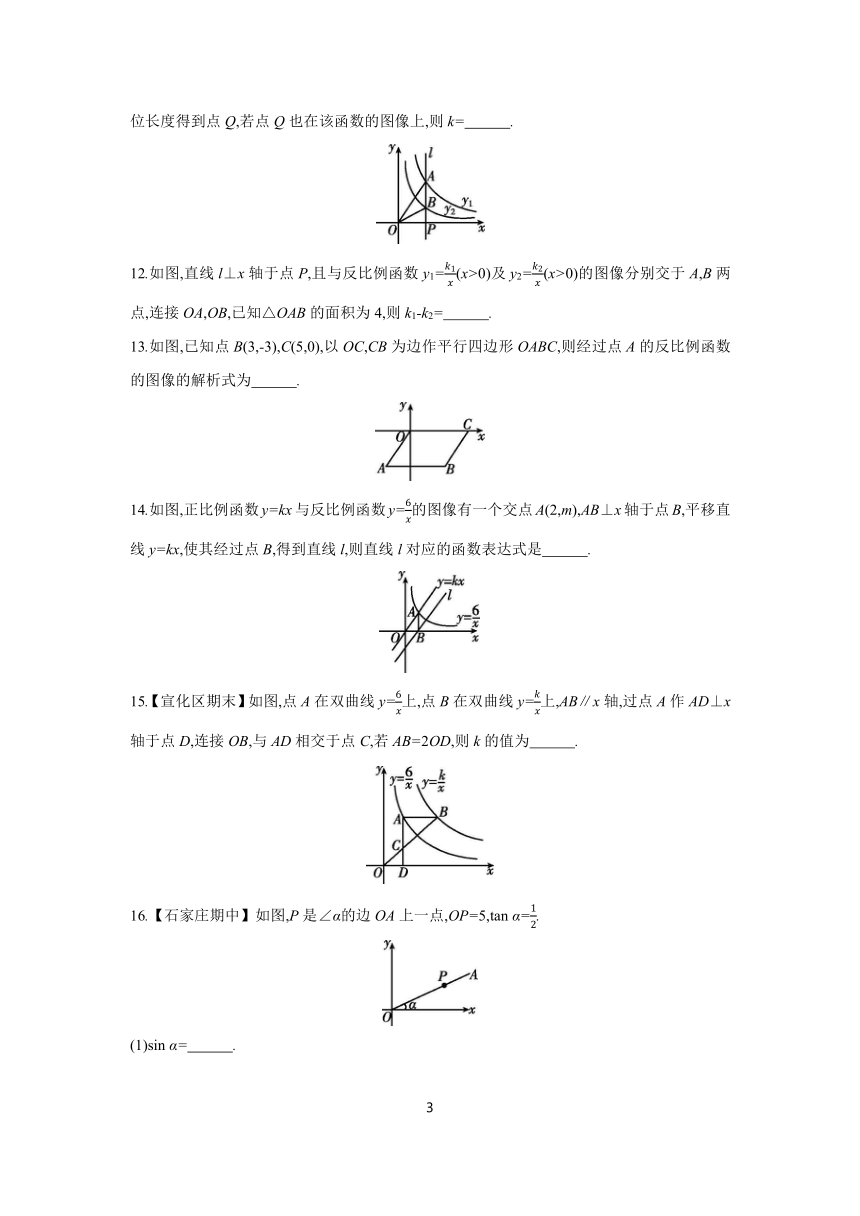
6.【路北区期末】如图,双曲线y=的一个分支为 ( )
A.① B.② C.③ D.④
7.【石家庄期中】如图,在平面直角坐标系中有一矩形ABCD灰色区域,其中AB=1,AD=4,点C(2,1),有一动态扫描线为双曲线y=(x>0),当扫描线遇到灰色区域时,区域便由灰变亮,则下列能够使灰色区域变亮的k的值不可能是 ( )
A.k=1 B.k=2.2 C.k= D.k=4
8.如图,反比例函数y=-与y=的图像上分别有一点A,B,且AB∥x轴,AD⊥x轴于点D,BC⊥x轴于点C,若矩形ABCD的面积为8,则a的值为 ( )
A.-2 B.-6 C.2 D.6
二、填空题(每小题3分,共24分)
9.若反比例函数的图像经过点(1,-2),则该反比例函数的解析式为 .
10.若一个反比例函数的图像经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为 .
11.反比例函数y=的图像上有一点P(2,n),将点P向右平移1个单位长度,再向下平移1个单位长度得到点Q,若点Q也在该函数的图像上,则k= .
12.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图像分别交于A,B两点,连接OA,OB,已知△OAB的面积为4,则k1-k2= .
13.如图,已知点B(3,-3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的图像的解析式为 .
14.如图,正比例函数y=kx与反比例函数y=的图像有一个交点A(2,m),AB⊥x轴于点B,平移直线y=kx,使其经过点B,得到直线l,则直线l对应的函数表达式是 .
15.【宣化区期末】如图,点A在双曲线y=上,点B在双曲线y=上,AB∥x轴,过点A作AD⊥x轴于点D,连接OB,与AD相交于点C,若AB=2OD,则k的值为 .
16.【石家庄期中】如图,P是∠α的边OA上一点,OP=5,tan α=.
(1)sin α= .
(2)若反比例函数y=的图像经过点P,则k= .
三、解答题(共52分)
17.(10分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)如果要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨
18.(10分)如图,一次函数y=kx+b的图像与反比例函数y=的图像相交于A(1,2),B(n,-1)两点.
(1)求一次函数和反比例函数的表达式.
(2)直线AB交x轴于点C,P是x轴上的点,若△ACP的面积是4,求点P的坐标.
19.(10分)如图,在Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y=(x>0)的图像上,直线AC⊥x轴,垂足为D,连接OA,OC,并延长OC交AB于点E,当AB=2OA时,E恰好为AB的中点,若∠AOD=45°,OA=2.
(1)求反比例函数的解析式.
(2)求∠EOD的度数.
20.(10分)某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
日销售单价x/元 3 4 5 6
日销售量y/只 2000 1500 1200 1000
(1)猜测并确定y与x之间的函数关系式.
(2)设经营此口罩的销售利润为W元,求出W与x之间的函数关系式.
(3)若物价局规定此口罩的售价最高不能超过10元/只,则当日销售单价x定为多少时,才能获得最大日销售利润 最大利润是多少元
21.(12分)长为300 m的春游队伍,以v(m/s)的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他和队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾的过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围).
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
参考答案
1.B 2.D 3.A 4.A
5.A 【解析】根据反比例函数k的几何意义可知,△AOP的面积为,△BOP的面积为,
∴△AOB的面积为-=(k1-k2).
∵k1=k2+2,
∴k1-k2=2,
∴△AOB的面积为×2=1.
故选A.
6.D
7.A 【解析】∵AB=1,AD=4,点C(2,1),
∴A(6,2).
当双曲线y=(x>0)经过点C时,开始能使灰色区域变亮,
将点C(2,1)代入可得k=2,
当双曲线y=(x>0)经过点A时,开始不能使灰色区域变亮,
将点A(6,2)代入可得k=12,
∴能够使灰色区域变亮的k的取值范围是2≤k≤12.
∴能够使灰色区域变亮的k的值不可能是选项A.
故选A.
8.C 【解析】如图,∵AB∥x轴,AD⊥x轴于点D,BC⊥x轴于点C,
∴S矩形ADOE=|-a|,S矩形BCOE=6.
∵矩形ABCD的面积为8,
∴S矩形ADOE+S矩形BCOE=S矩形ABCD=8,
∴|-a|+6=8.
∵反比例函数y=-的图像在第二象限,
∴a>0,
∴a=2.
故选C.
9.y=- 10.y= 11.6 12.8 13.y=
14.y=x-3
15.【解析】如图,过点B作BE⊥x轴于点E,延长线段BA,交y轴于点F.
∵AB∥x轴,
∴AF⊥y轴,
∴四边形AFOD是矩形,四边形OEBF是矩形,
∴AF=OD,BF=OE,
∴AB=DE.
∵点A在双曲线y=上,
∴S矩形AFOD=6,
同理S矩形OEBF=k.
∵AB=2OD,
∴DE=2OD,
∴S矩形OEBF=3S矩形AFOD=18,
∴k=18.
故答案是18.
16.(1) (2)10
17.【解析】(1)由题意可得100=vt,
则v=,t>0.
(2)∵要求不超过5小时卸完船上的这批货物,
∴t≤5,
则v≥=20.
答:平均每小时至少要卸货20吨.
18.【解析】(1)将点A(1,2)代入y=,得m=2,
∴y=,
当y=-1时,x=-2,
∴B点坐标为(-2,-1),
将A(1,2),B(-2,-1)代入y=kx+b,
得
解得
∴y=x+1.
∴一次函数的解析式为y=x+1,反比例函数的解析式为y=.
(2)在y=x+1中,当y=0时,x+1=0,
解得x=-1,
∴C点坐标为(-1,0),
设P点坐标为(m,0),
则PC=|-1-m|.
∵S△ACP=·PC·yA=4,
∴×|-1-m|×2=4,
解得m=3或m=-5,
∴点P的坐标为(3,0)或(-5,0).
19.【解析】(1)∵直线AC⊥x轴,垂足为D,∠AOD=45°,
∴△AOD是等腰直角三角形.
∵OA=2,
∴OD=AD=2,
∴A点坐标为(2,2).
∵顶点A在反比例函数y=(x>0)的图像上,
∴k=2×2=4,
∴反比例函数的解析式为y=.
(2)∵AB=2OA,E恰好为AB的中点,
∴OA=AE.
∵在Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC.
∵∠AEO=∠ECB+∠EBC=2∠EBC,
又BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD.
∵∠AOD=45°,
∴∠EOD=15°.
20.【解析】(1)由表可知,xy=6000,
∴y=(x>0).
(2)根据题意,
得W=(x-2)·y=(x-2)·=6000-.
(3)∵x≤10,
∴6000-≤4800,
即当x=10时,W取得最大值,最大值为4800元.
答:当日销售单价x定为10元时,才能获得最大日销售利润,最大利润是4800元.
21.【解析】(1)①排尾从位置O开始行进的时间为t(s),则排头行进的时间也是t(s),
故S头=2t+300.
②甲从排尾赶到排头的时间为300÷(2v-v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m.
∵甲返回时间为(t-150)s,
∴S甲=S头-S甲回=2×150+300-4(t-150)=-4t+1200,
∴当甲赶到排头位置时,S的值为600 m;在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=-4t+1200.
(2)T=t追及+t返回=+=,
在甲这次往返队伍的过程中队伍行进的路程为v×T=v×=400.
因此T与v的函数关系式为T=,此时队伍在此过程中行进的路程为400 m.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共24分)
1.下列函数中是反比例函数的是 ( )
A.y=x+1 B.y=
C.y=-2x D.y=2x2
2.【宣化区期末】若反比例函数y=的图像经过点(-1,-2),则k的值是 ( )
A.2 B.-2 C.-3 D.3
3.已知ab<0,一次函数y=ax-b与反比例函数y=在同一直角坐标系中的图像可能是 ( )
A. B.
C. D.
4.如图,这是三个反比例函数y1=,y2=,y3=在y轴右边的图像,由此观察得到k1,k2,k3的大小关系是 ( )
A.k1>k2>k3 B.k1>k3>k2
C.k2>k3>k1 D.k3>k2>k1
5.【路北区期末】如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图像分别交于点A,B,连接OA,OB,已知k1=k2+2,则△OAB的面积是 ( )
A.1 B.2 C.4 D.0.5
6.【路北区期末】如图,双曲线y=的一个分支为 ( )
A.① B.② C.③ D.④
7.【石家庄期中】如图,在平面直角坐标系中有一矩形ABCD灰色区域,其中AB=1,AD=4,点C(2,1),有一动态扫描线为双曲线y=(x>0),当扫描线遇到灰色区域时,区域便由灰变亮,则下列能够使灰色区域变亮的k的值不可能是 ( )
A.k=1 B.k=2.2 C.k= D.k=4
8.如图,反比例函数y=-与y=的图像上分别有一点A,B,且AB∥x轴,AD⊥x轴于点D,BC⊥x轴于点C,若矩形ABCD的面积为8,则a的值为 ( )
A.-2 B.-6 C.2 D.6
二、填空题(每小题3分,共24分)
9.若反比例函数的图像经过点(1,-2),则该反比例函数的解析式为 .
10.若一个反比例函数的图像经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为 .
11.反比例函数y=的图像上有一点P(2,n),将点P向右平移1个单位长度,再向下平移1个单位长度得到点Q,若点Q也在该函数的图像上,则k= .
12.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图像分别交于A,B两点,连接OA,OB,已知△OAB的面积为4,则k1-k2= .
13.如图,已知点B(3,-3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的图像的解析式为 .
14.如图,正比例函数y=kx与反比例函数y=的图像有一个交点A(2,m),AB⊥x轴于点B,平移直线y=kx,使其经过点B,得到直线l,则直线l对应的函数表达式是 .
15.【宣化区期末】如图,点A在双曲线y=上,点B在双曲线y=上,AB∥x轴,过点A作AD⊥x轴于点D,连接OB,与AD相交于点C,若AB=2OD,则k的值为 .
16.【石家庄期中】如图,P是∠α的边OA上一点,OP=5,tan α=.
(1)sin α= .
(2)若反比例函数y=的图像经过点P,则k= .
三、解答题(共52分)
17.(10分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式.
(2)如果要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨
18.(10分)如图,一次函数y=kx+b的图像与反比例函数y=的图像相交于A(1,2),B(n,-1)两点.
(1)求一次函数和反比例函数的表达式.
(2)直线AB交x轴于点C,P是x轴上的点,若△ACP的面积是4,求点P的坐标.
19.(10分)如图,在Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y=(x>0)的图像上,直线AC⊥x轴,垂足为D,连接OA,OC,并延长OC交AB于点E,当AB=2OA时,E恰好为AB的中点,若∠AOD=45°,OA=2.
(1)求反比例函数的解析式.
(2)求∠EOD的度数.
20.(10分)某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
日销售单价x/元 3 4 5 6
日销售量y/只 2000 1500 1200 1000
(1)猜测并确定y与x之间的函数关系式.
(2)设经营此口罩的销售利润为W元,求出W与x之间的函数关系式.
(3)若物价局规定此口罩的售价最高不能超过10元/只,则当日销售单价x定为多少时,才能获得最大日销售利润 最大利润是多少元
21.(12分)长为300 m的春游队伍,以v(m/s)的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他和队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾的过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围).
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
参考答案
1.B 2.D 3.A 4.A
5.A 【解析】根据反比例函数k的几何意义可知,△AOP的面积为,△BOP的面积为,
∴△AOB的面积为-=(k1-k2).
∵k1=k2+2,
∴k1-k2=2,
∴△AOB的面积为×2=1.
故选A.
6.D
7.A 【解析】∵AB=1,AD=4,点C(2,1),
∴A(6,2).
当双曲线y=(x>0)经过点C时,开始能使灰色区域变亮,
将点C(2,1)代入可得k=2,
当双曲线y=(x>0)经过点A时,开始不能使灰色区域变亮,
将点A(6,2)代入可得k=12,
∴能够使灰色区域变亮的k的取值范围是2≤k≤12.
∴能够使灰色区域变亮的k的值不可能是选项A.
故选A.
8.C 【解析】如图,∵AB∥x轴,AD⊥x轴于点D,BC⊥x轴于点C,
∴S矩形ADOE=|-a|,S矩形BCOE=6.
∵矩形ABCD的面积为8,
∴S矩形ADOE+S矩形BCOE=S矩形ABCD=8,
∴|-a|+6=8.
∵反比例函数y=-的图像在第二象限,
∴a>0,
∴a=2.
故选C.
9.y=- 10.y= 11.6 12.8 13.y=
14.y=x-3
15.【解析】如图,过点B作BE⊥x轴于点E,延长线段BA,交y轴于点F.
∵AB∥x轴,
∴AF⊥y轴,
∴四边形AFOD是矩形,四边形OEBF是矩形,
∴AF=OD,BF=OE,
∴AB=DE.
∵点A在双曲线y=上,
∴S矩形AFOD=6,
同理S矩形OEBF=k.
∵AB=2OD,
∴DE=2OD,
∴S矩形OEBF=3S矩形AFOD=18,
∴k=18.
故答案是18.
16.(1) (2)10
17.【解析】(1)由题意可得100=vt,
则v=,t>0.
(2)∵要求不超过5小时卸完船上的这批货物,
∴t≤5,
则v≥=20.
答:平均每小时至少要卸货20吨.
18.【解析】(1)将点A(1,2)代入y=,得m=2,
∴y=,
当y=-1时,x=-2,
∴B点坐标为(-2,-1),
将A(1,2),B(-2,-1)代入y=kx+b,
得
解得
∴y=x+1.
∴一次函数的解析式为y=x+1,反比例函数的解析式为y=.
(2)在y=x+1中,当y=0时,x+1=0,
解得x=-1,
∴C点坐标为(-1,0),
设P点坐标为(m,0),
则PC=|-1-m|.
∵S△ACP=·PC·yA=4,
∴×|-1-m|×2=4,
解得m=3或m=-5,
∴点P的坐标为(3,0)或(-5,0).
19.【解析】(1)∵直线AC⊥x轴,垂足为D,∠AOD=45°,
∴△AOD是等腰直角三角形.
∵OA=2,
∴OD=AD=2,
∴A点坐标为(2,2).
∵顶点A在反比例函数y=(x>0)的图像上,
∴k=2×2=4,
∴反比例函数的解析式为y=.
(2)∵AB=2OA,E恰好为AB的中点,
∴OA=AE.
∵在Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC.
∵∠AEO=∠ECB+∠EBC=2∠EBC,
又BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD.
∵∠AOD=45°,
∴∠EOD=15°.
20.【解析】(1)由表可知,xy=6000,
∴y=(x>0).
(2)根据题意,
得W=(x-2)·y=(x-2)·=6000-.
(3)∵x≤10,
∴6000-≤4800,
即当x=10时,W取得最大值,最大值为4800元.
答:当日销售单价x定为10元时,才能获得最大日销售利润,最大利润是4800元.
21.【解析】(1)①排尾从位置O开始行进的时间为t(s),则排头行进的时间也是t(s),
故S头=2t+300.
②甲从排尾赶到排头的时间为300÷(2v-v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m.
∵甲返回时间为(t-150)s,
∴S甲=S头-S甲回=2×150+300-4(t-150)=-4t+1200,
∴当甲赶到排头位置时,S的值为600 m;在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=-4t+1200.
(2)T=t追及+t返回=+=,
在甲这次往返队伍的过程中队伍行进的路程为v×T=v×=400.
因此T与v的函数关系式为T=,此时队伍在此过程中行进的路程为400 m.
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
