第28章 圆单元测试题 (含答案) 2023-2024学年初中数学冀教版九年级上册
文档属性
| 名称 | 第28章 圆单元测试题 (含答案) 2023-2024学年初中数学冀教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 293.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览



文档简介
第二十八章 圆 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共36分)
1.能说明圆上一条弧所对的圆周角等于它所对圆心角的一半的图形是 ( )
A. B.
C. D.
2.如图,M是☉O上的任意一点,有下列结论:
①以M为端点的弦只有一条;
②以M为端点的直径只有一条;
③以M为端点的弧只有一条.
则 ( )
A.①②错误,③正确
B.②③错误,①正确
C.①③错误,②正确
D.①②③错误
3.【路北区期末】如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是 ( )
A.115°
B.105°
C.100°
D.95°
4.已知一条圆弧长为10π,对应的圆心角的度数为60°,则此圆弧的半径为 ( )
A.15 B.30
C. D.15π
5.如图,AB是☉O的直径,点C,D在☉O上,且在AB异侧,连接OC,CD,DA.若∠BOC=130°,则∠D的度数为 ( )
A.15°
B.25°
C.35°
D.50°
6.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是 ( )
A. B.
C. D.
7.已知点O是△ABC的外心,连接OB,若∠OBC=28°,则∠A的度数为 ( )
A.28°
B.52°
C.56°
D.62°
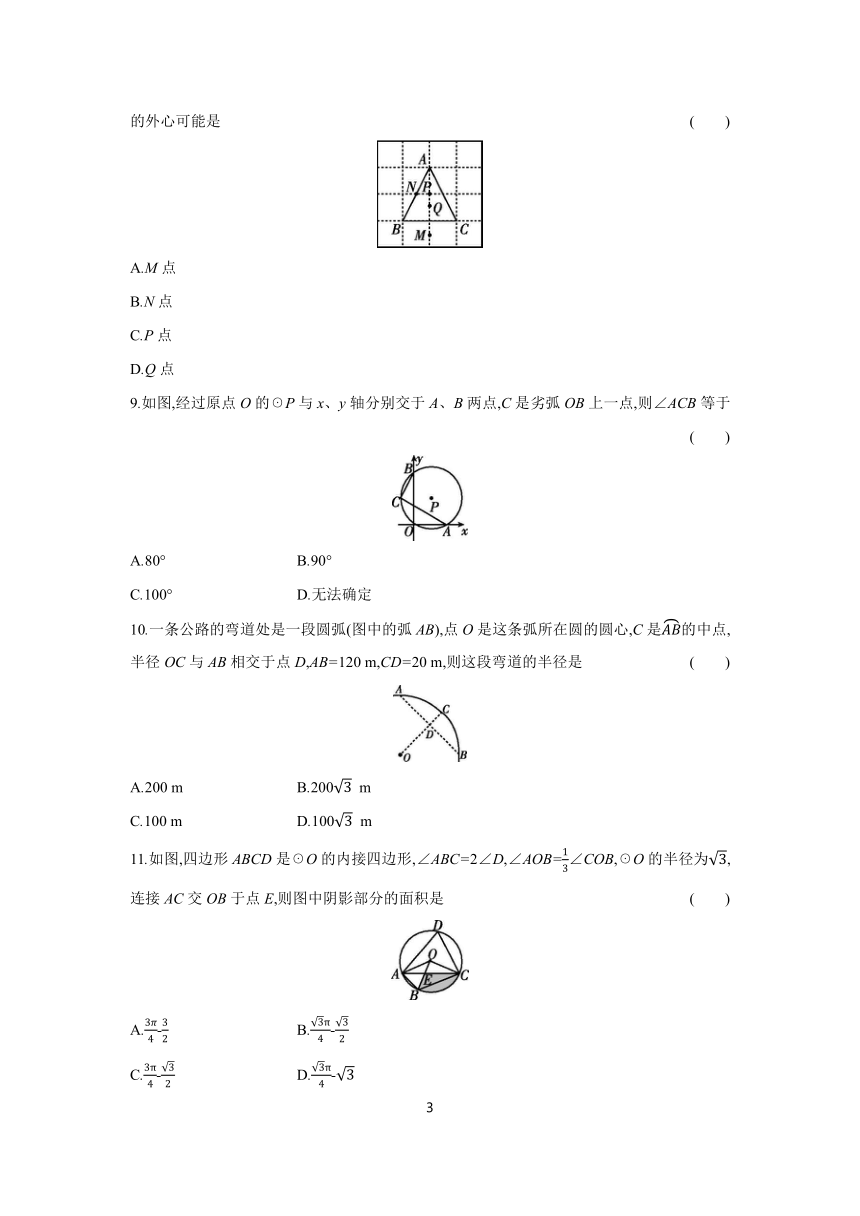
8.【保定模拟】如图,在4×4的网格中,每个小正方形的边长均为1,A,B,C是三个格点,则△ABC的外心可能是 ( )
A.M点
B.N点
C.P点
D.Q点
9.如图,经过原点O的☉P与x、y轴分别交于A、B两点,C是劣弧OB上一点,则∠ACB等于 ( )
A.80° B.90°
C.100° D.无法确定
10.一条公路的弯道处是一段圆弧(图中的弧AB),点O是这条弧所在圆的圆心,C是的中点,半径OC与AB相交于点D,AB=120 m,CD=20 m,则这段弯道的半径是 ( )
A.200 m B.200 m
C.100 m D.100 m
11.如图,四边形ABCD是☉O的内接四边形,∠ABC=2∠D,∠AOB=∠COB,☉O的半径为,连接AC交OB于点E,则图中阴影部分的面积是 ( )
A.- B.-
C.- D.-
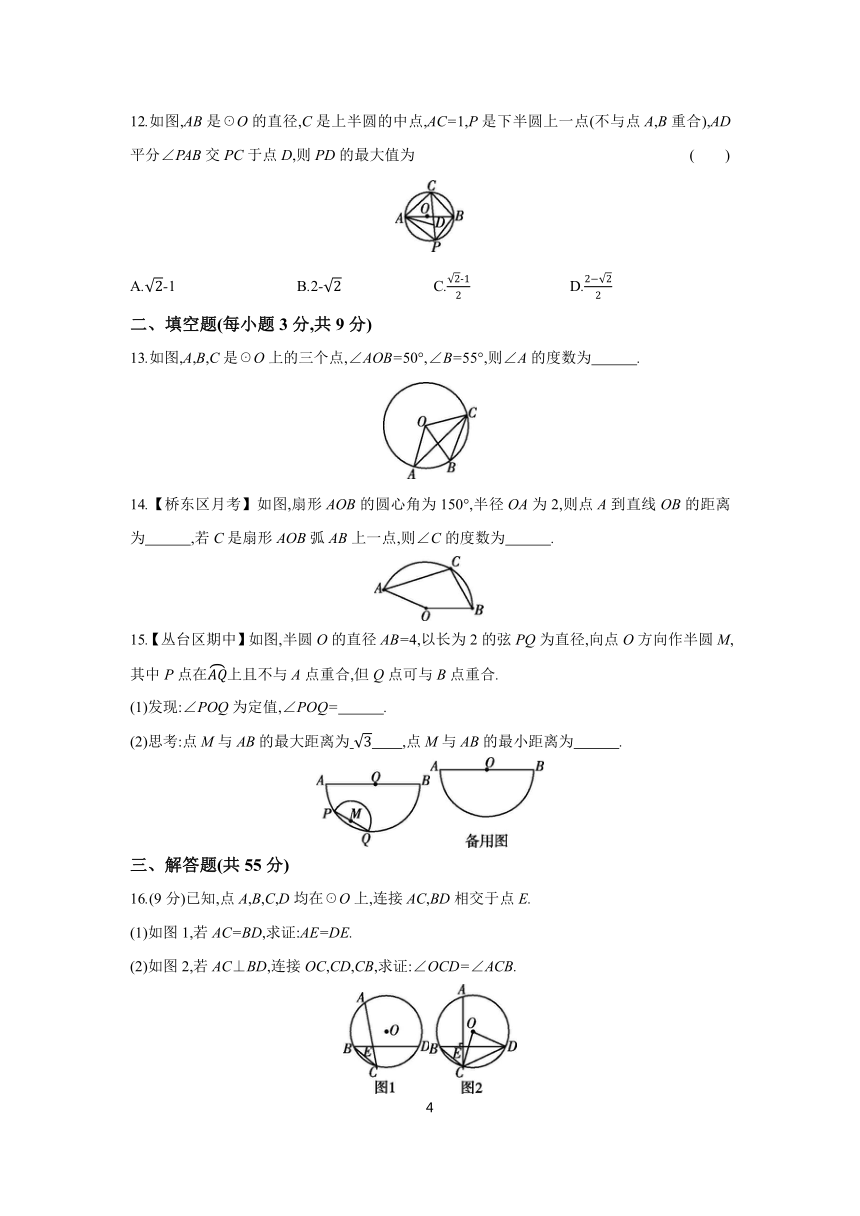
12.如图,AB是☉O的直径,C是上半圆的中点,AC=1,P是下半圆上一点(不与点A,B重合),AD平分∠PAB交PC于点D,则PD的最大值为 ( )
A.-1 B.2- C. D.
二、填空题(每小题3分,共9分)
13.如图,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
14.【桥东区月考】如图,扇形AOB的圆心角为150°,半径OA为2,则点A到直线OB的距离为 ,若C是扇形AOB弧AB上一点,则∠C的度数为 .
15.【丛台区期中】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在上且不与A点重合,但Q点可与B点重合.
(1)发现:∠POQ为定值,∠POQ= .
(2)思考:点M与AB的最大距离为 ,点M与AB的最小距离为 .
三、解答题(共55分)
16.(9分)已知,点A,B,C,D均在☉O上,连接AC,BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE.
(2)如图2,若AC⊥BD,连接OC,CD,CB,求证:∠OCD=∠ACB.
17.(9分)如图,在△ABC中,AB=AC,以AB为直径作☉O,交BC于点D,交CA的延长线于点E,连接AD,DE.
(1)求证:D是BC的中点.
(2)若DE=4,AD=2,求☉O的半径.
18.(9分)如图,以 ABCD的顶点A为圆心,AB为半径作☉A,分别交BC、AD于E、F两点,交BA的延长线于点G,判断弧和弧是否相等,并说明理由.
19.(9分)【路北区期末】如图,在半径为2的☉O中,弦AB⊥直径CD,垂足为E,∠ACD=30°,P为☉O上一动点,CF⊥AP于点F.
(1)求弦AB的长度.
(2)求点P在☉O上运动的过程中,线段OF长度的最小值.
20.(9分)如图,已知△ABC内接于☉O,AF是☉O的弦,AF⊥BC,垂足为D,E为弧BF上一点,且BE=CF.
(1)求证:AE是☉O的直径.
(2)若∠ABC=∠EAC,AE=8,求AC的长.
21.(10分)如图,☉O的内接四边形ABCD的两组对边的延长线分别交于点E、F.
(1)若∠E=∠F,求证:∠ADC=∠ABC.
(2)若∠E=∠F=42°,求∠A的度数.
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
参考答案
1.A 2.C 3.B 4.B 5.B 6.C 7.D 8.D 9.B
10.C
11.C 【解析】∵四边形ABCD是☉O的内接四边形,
∴∠ABC+∠ADC=180°.
又∵∠ABC=2∠D,
∴∠ABC=120°,∠D=60°,
∴∠AOC=2∠D=120°.
∵∠AOB=∠COB,
∴∠AOB=30°,∠COB=90°.
在△AOC中,OA=OC,∠AOC=120°,
∴∠OCE=∠OAE=30°.
在Rt△COE中,☉O的半径为,即OC=OB=OA=,∠OCE=30°,
∴OE=OC=1,
∴S阴影部分=S扇形BOC-S△COE
=-×1×
=-.
故选C.
12.A 【解析】∵C是上半圆的中点,
∴=,
∴∠APC=∠BPC=45°.
∵AB是☉O的直径,C是上半圆的中点,
∴∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°.
∵AD平分∠PAB,
∴∠PAD=∠BAD.
∵∠CAD=∠CAB+∠BAD=45°+∠BAD,
∠CDA=∠APC+∠PAD=45°+∠PAD,
∴∠CAD=∠CDA,
∴CD=CA=1,
∴PD=PC-CD=PC-1,
∴当PC取最大值时,PD有最大值.
∵直径是圆中最长的弦,
∴当PC为圆的直径时,PC取最大值.
∵AB===,
∴PC的最大值=AB=,
∴PD的最大值为-1.
故选A.
13.30°
14.1 105° 【解析】如图,补全圆O,过点A作AH⊥OB交BO的延长线于点H,作弧ACB所对的圆周角∠ADB.
∵∠AOB=150°,
∴∠AOH=30°,
∴AH=OA=1,
即点A到直线OB的距离为1.
∵∠D=∠AOB=×150°=75°,
而∠C+∠D=180°,
∴∠C=180°-75°=105°.
15.(1)60° (2) 【解析】(1)如图1,连接OP,OQ.
∵AB=4,
∴OP=OQ=2.
∵PQ=2,
∴△OPQ是等边三角形,
∴∠POQ=60°.
故答案为60°.
(2)如图2,过点M作MC⊥AB于点C,
连接OM,
∵OP=2,PM=1,
∴由勾股定理可知OM=,
当C与O重合时,
点M与AB的距离最大,最大值为.
如图3,当点Q与点B重合时,设半圆M与半圆O相交于点D,连接DM,OM.
∵∠MOQ=30°,
∴MC=OM=,
此时点M与AB的距离最小,最小值为.
故答案为;.
16.【解析】证明:(1)∵AC=BD,
∴=,
∴-=-,即=,
∴∠ACB=∠DBC,
∴EB=EC,
∴AE=DE.
(2)如图,延长CO交☉O于点F,连接DF,
则CF为☉O的直径,
∴∠CDF=90°,
∴∠OCD+∠F=90°.
∵AC⊥BD,
∴∠ACB+∠B=90°,
由圆周角定理得∠B=∠F,
∴∠OCD=∠ACB.
17.【解析】(1)证明:∵AB是☉O的直径,
∴∠ADB=90°,
∴AD⊥BC.
∵AB=AC,
∴DB=DC,
即D是BC的中点.
(2)∵AB=AC,
∴∠B=∠C.
又∵∠B=∠E,
∴∠C=∠E,
∴DE=DC.
∵DC=BD,DE=4,
∴DE=BD=4.
在Rt△ADB中,AD=2,
AB===2,
∴☉O 的半径为=.
18.【解析】 =.
理由:如图,连接AE,
则AB=AE,
∴∠B=∠AEB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴=.
19.【解析】(1)如图,连接OA.
∵OA=OC=2,
∴∠OCA=∠OAC=30°,
∴∠AOE=∠OAC+∠ACO=60°,
∴AE=OA·sin 60°=.
∵OE⊥AB,
∴AE=EB=,
∴AB=2AE=2.
(2)如图,取AC的中点H,连接OH,OF,HF.
∵OA=OC,AH=HC,
∴OH⊥AC,
∴∠AHO=90°.
∵∠HCO=30°,
∴∠COH=60°,
∴OH=OC=1,HC=,AC=2.
∵CF⊥AP,
∴∠AFC=90°,
∴HF=AC=,
∴OF≥FH-OH,即OF≥-1,
∴OF的最小值为-1.
20.【解析】(1)证明:∵BE=CF,∴=,∴∠BAE=∠CAF.∵AF⊥BC,∴∠ADC=90°,∴∠FAC+∠ACB=90°.∵∠E=∠ACB,∴∠E+∠BAE=90°,∴∠ABE=90°,∴AE是☉O的直径.
(2)如图,连接OC,
∴∠AOC=2∠ABC.∵∠ABC=∠CAE,∴∠AOC=2∠CAE.∵OA=OC,∴∠CAO=∠ACO=∠AOC,∴△AOC是等腰直角三角形.∵AE=8,∴AO=CO=4,∴AC=4.
21.【解析】(1)证明:∵∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,而∠E=∠F,∠DCE=∠BCF,
∴∠ADC=∠ABC.
(2)由(1)知∠ADC=∠ABC,
∵∠EDC和∠ABC都与∠ADC互补,
∴∠EDC=∠ABC,
∴∠EDC=∠ADC=90°.
∵∠DCE+∠BCD=180°,
∠BCD+∠A=180°,∴∠DCE=∠A,
∴∠A=90°-42°=48°.
(3)如图,连接EF.
∵四边形ABCD为圆的内接四边形,
∴∠A与∠BCD互补.
又∵∠ECD与∠BCD互补,
∴∠ECD=∠A.
∵∠ECD=∠1+∠2,
∴∠A=∠1+∠2.
∵∠A+∠1+∠2+∠E+∠F=180°,
∴2∠A+α+β=180°,
∴∠A=90°-.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共36分)
1.能说明圆上一条弧所对的圆周角等于它所对圆心角的一半的图形是 ( )
A. B.
C. D.
2.如图,M是☉O上的任意一点,有下列结论:
①以M为端点的弦只有一条;
②以M为端点的直径只有一条;
③以M为端点的弧只有一条.
则 ( )
A.①②错误,③正确
B.②③错误,①正确
C.①③错误,②正确
D.①②③错误
3.【路北区期末】如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是 ( )
A.115°
B.105°
C.100°
D.95°
4.已知一条圆弧长为10π,对应的圆心角的度数为60°,则此圆弧的半径为 ( )
A.15 B.30
C. D.15π
5.如图,AB是☉O的直径,点C,D在☉O上,且在AB异侧,连接OC,CD,DA.若∠BOC=130°,则∠D的度数为 ( )
A.15°
B.25°
C.35°
D.50°
6.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是 ( )
A. B.
C. D.
7.已知点O是△ABC的外心,连接OB,若∠OBC=28°,则∠A的度数为 ( )
A.28°
B.52°
C.56°
D.62°
8.【保定模拟】如图,在4×4的网格中,每个小正方形的边长均为1,A,B,C是三个格点,则△ABC的外心可能是 ( )
A.M点
B.N点
C.P点
D.Q点
9.如图,经过原点O的☉P与x、y轴分别交于A、B两点,C是劣弧OB上一点,则∠ACB等于 ( )
A.80° B.90°
C.100° D.无法确定
10.一条公路的弯道处是一段圆弧(图中的弧AB),点O是这条弧所在圆的圆心,C是的中点,半径OC与AB相交于点D,AB=120 m,CD=20 m,则这段弯道的半径是 ( )
A.200 m B.200 m
C.100 m D.100 m
11.如图,四边形ABCD是☉O的内接四边形,∠ABC=2∠D,∠AOB=∠COB,☉O的半径为,连接AC交OB于点E,则图中阴影部分的面积是 ( )
A.- B.-
C.- D.-
12.如图,AB是☉O的直径,C是上半圆的中点,AC=1,P是下半圆上一点(不与点A,B重合),AD平分∠PAB交PC于点D,则PD的最大值为 ( )
A.-1 B.2- C. D.
二、填空题(每小题3分,共9分)
13.如图,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
14.【桥东区月考】如图,扇形AOB的圆心角为150°,半径OA为2,则点A到直线OB的距离为 ,若C是扇形AOB弧AB上一点,则∠C的度数为 .
15.【丛台区期中】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在上且不与A点重合,但Q点可与B点重合.
(1)发现:∠POQ为定值,∠POQ= .
(2)思考:点M与AB的最大距离为 ,点M与AB的最小距离为 .
三、解答题(共55分)
16.(9分)已知,点A,B,C,D均在☉O上,连接AC,BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE.
(2)如图2,若AC⊥BD,连接OC,CD,CB,求证:∠OCD=∠ACB.
17.(9分)如图,在△ABC中,AB=AC,以AB为直径作☉O,交BC于点D,交CA的延长线于点E,连接AD,DE.
(1)求证:D是BC的中点.
(2)若DE=4,AD=2,求☉O的半径.
18.(9分)如图,以 ABCD的顶点A为圆心,AB为半径作☉A,分别交BC、AD于E、F两点,交BA的延长线于点G,判断弧和弧是否相等,并说明理由.
19.(9分)【路北区期末】如图,在半径为2的☉O中,弦AB⊥直径CD,垂足为E,∠ACD=30°,P为☉O上一动点,CF⊥AP于点F.
(1)求弦AB的长度.
(2)求点P在☉O上运动的过程中,线段OF长度的最小值.
20.(9分)如图,已知△ABC内接于☉O,AF是☉O的弦,AF⊥BC,垂足为D,E为弧BF上一点,且BE=CF.
(1)求证:AE是☉O的直径.
(2)若∠ABC=∠EAC,AE=8,求AC的长.
21.(10分)如图,☉O的内接四边形ABCD的两组对边的延长线分别交于点E、F.
(1)若∠E=∠F,求证:∠ADC=∠ABC.
(2)若∠E=∠F=42°,求∠A的度数.
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
参考答案
1.A 2.C 3.B 4.B 5.B 6.C 7.D 8.D 9.B
10.C
11.C 【解析】∵四边形ABCD是☉O的内接四边形,
∴∠ABC+∠ADC=180°.
又∵∠ABC=2∠D,
∴∠ABC=120°,∠D=60°,
∴∠AOC=2∠D=120°.
∵∠AOB=∠COB,
∴∠AOB=30°,∠COB=90°.
在△AOC中,OA=OC,∠AOC=120°,
∴∠OCE=∠OAE=30°.
在Rt△COE中,☉O的半径为,即OC=OB=OA=,∠OCE=30°,
∴OE=OC=1,
∴S阴影部分=S扇形BOC-S△COE
=-×1×
=-.
故选C.
12.A 【解析】∵C是上半圆的中点,
∴=,
∴∠APC=∠BPC=45°.
∵AB是☉O的直径,C是上半圆的中点,
∴∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°.
∵AD平分∠PAB,
∴∠PAD=∠BAD.
∵∠CAD=∠CAB+∠BAD=45°+∠BAD,
∠CDA=∠APC+∠PAD=45°+∠PAD,
∴∠CAD=∠CDA,
∴CD=CA=1,
∴PD=PC-CD=PC-1,
∴当PC取最大值时,PD有最大值.
∵直径是圆中最长的弦,
∴当PC为圆的直径时,PC取最大值.
∵AB===,
∴PC的最大值=AB=,
∴PD的最大值为-1.
故选A.
13.30°
14.1 105° 【解析】如图,补全圆O,过点A作AH⊥OB交BO的延长线于点H,作弧ACB所对的圆周角∠ADB.
∵∠AOB=150°,
∴∠AOH=30°,
∴AH=OA=1,
即点A到直线OB的距离为1.
∵∠D=∠AOB=×150°=75°,
而∠C+∠D=180°,
∴∠C=180°-75°=105°.
15.(1)60° (2) 【解析】(1)如图1,连接OP,OQ.
∵AB=4,
∴OP=OQ=2.
∵PQ=2,
∴△OPQ是等边三角形,
∴∠POQ=60°.
故答案为60°.
(2)如图2,过点M作MC⊥AB于点C,
连接OM,
∵OP=2,PM=1,
∴由勾股定理可知OM=,
当C与O重合时,
点M与AB的距离最大,最大值为.
如图3,当点Q与点B重合时,设半圆M与半圆O相交于点D,连接DM,OM.
∵∠MOQ=30°,
∴MC=OM=,
此时点M与AB的距离最小,最小值为.
故答案为;.
16.【解析】证明:(1)∵AC=BD,
∴=,
∴-=-,即=,
∴∠ACB=∠DBC,
∴EB=EC,
∴AE=DE.
(2)如图,延长CO交☉O于点F,连接DF,
则CF为☉O的直径,
∴∠CDF=90°,
∴∠OCD+∠F=90°.
∵AC⊥BD,
∴∠ACB+∠B=90°,
由圆周角定理得∠B=∠F,
∴∠OCD=∠ACB.
17.【解析】(1)证明:∵AB是☉O的直径,
∴∠ADB=90°,
∴AD⊥BC.
∵AB=AC,
∴DB=DC,
即D是BC的中点.
(2)∵AB=AC,
∴∠B=∠C.
又∵∠B=∠E,
∴∠C=∠E,
∴DE=DC.
∵DC=BD,DE=4,
∴DE=BD=4.
在Rt△ADB中,AD=2,
AB===2,
∴☉O 的半径为=.
18.【解析】 =.
理由:如图,连接AE,
则AB=AE,
∴∠B=∠AEB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴=.
19.【解析】(1)如图,连接OA.
∵OA=OC=2,
∴∠OCA=∠OAC=30°,
∴∠AOE=∠OAC+∠ACO=60°,
∴AE=OA·sin 60°=.
∵OE⊥AB,
∴AE=EB=,
∴AB=2AE=2.
(2)如图,取AC的中点H,连接OH,OF,HF.
∵OA=OC,AH=HC,
∴OH⊥AC,
∴∠AHO=90°.
∵∠HCO=30°,
∴∠COH=60°,
∴OH=OC=1,HC=,AC=2.
∵CF⊥AP,
∴∠AFC=90°,
∴HF=AC=,
∴OF≥FH-OH,即OF≥-1,
∴OF的最小值为-1.
20.【解析】(1)证明:∵BE=CF,∴=,∴∠BAE=∠CAF.∵AF⊥BC,∴∠ADC=90°,∴∠FAC+∠ACB=90°.∵∠E=∠ACB,∴∠E+∠BAE=90°,∴∠ABE=90°,∴AE是☉O的直径.
(2)如图,连接OC,
∴∠AOC=2∠ABC.∵∠ABC=∠CAE,∴∠AOC=2∠CAE.∵OA=OC,∴∠CAO=∠ACO=∠AOC,∴△AOC是等腰直角三角形.∵AE=8,∴AO=CO=4,∴AC=4.
21.【解析】(1)证明:∵∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,而∠E=∠F,∠DCE=∠BCF,
∴∠ADC=∠ABC.
(2)由(1)知∠ADC=∠ABC,
∵∠EDC和∠ABC都与∠ADC互补,
∴∠EDC=∠ABC,
∴∠EDC=∠ADC=90°.
∵∠DCE+∠BCD=180°,
∠BCD+∠A=180°,∴∠DCE=∠A,
∴∠A=90°-42°=48°.
(3)如图,连接EF.
∵四边形ABCD为圆的内接四边形,
∴∠A与∠BCD互补.
又∵∠ECD与∠BCD互补,
∴∠ECD=∠A.
∵∠ECD=∠1+∠2,
∴∠A=∠1+∠2.
∵∠A+∠1+∠2+∠E+∠F=180°,
∴2∠A+α+β=180°,
∴∠A=90°-.
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
