第29章 直线与圆的位置关系同步练习 (含答案) 2023-2024学年初中数学冀教版九年级下册
文档属性
| 名称 | 第29章 直线与圆的位置关系同步练习 (含答案) 2023-2024学年初中数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 205.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 18:46:16 | ||
图片预览



文档简介
第二十九章 直线与圆的位置关系 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共30分)
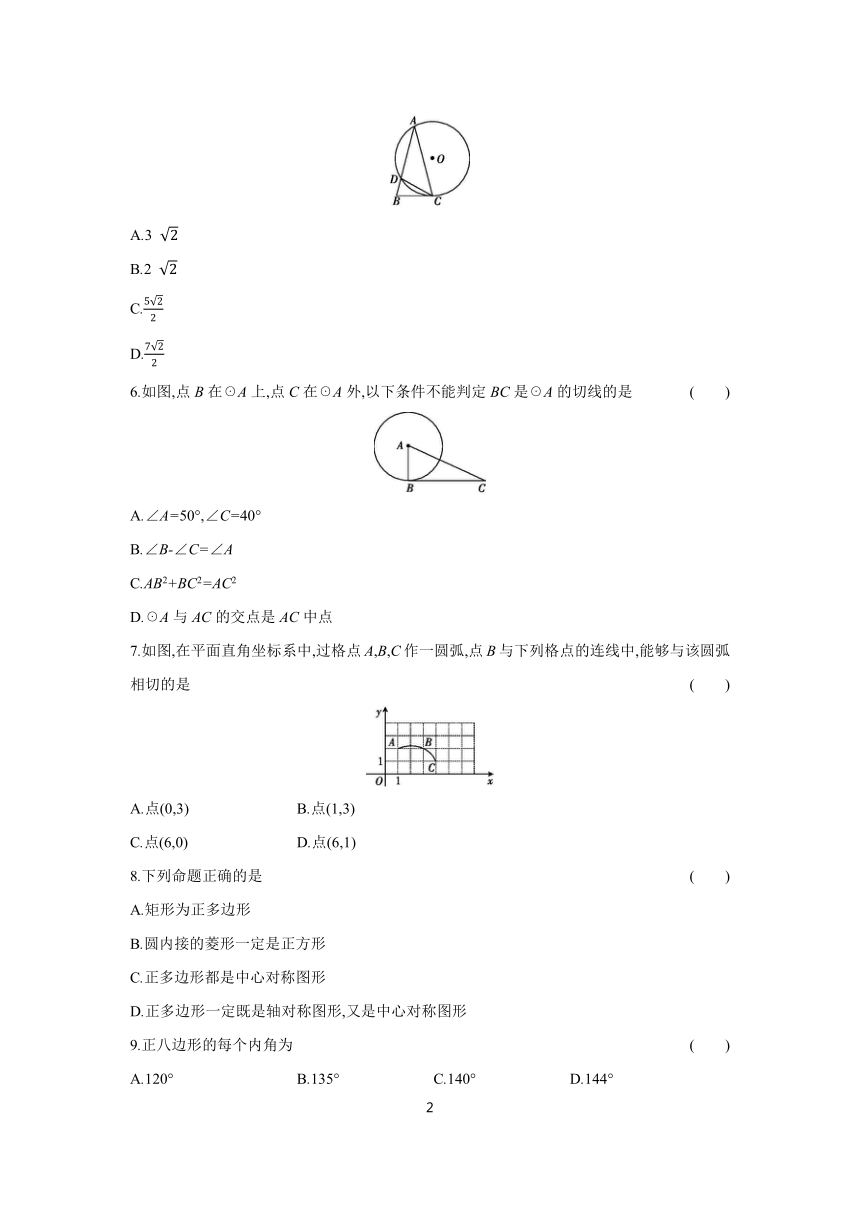
1.若☉O的半径为6,点O到直线l的距离为3,则下列图中位置关系正确的是 ( )
2.在平面直角坐标系中,以(-2,3)为圆心,3为半径的圆一定 ( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
3.如图,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C.若AB=8,OA=6,则BC的长为 ( )
A.3 B.4 C.5 D.6
4.如图,AB是半圆O的直径,C是BA延长线上一点,CD切半圆O于点E,BD⊥CD于点D,若CD=8,BD=6,则半圆O的半径为 ( )
A.3.5 B.4 C.2 D.3.75
5.如图,经过A,C两点的☉O与△ABC的边BC相切,与边AB交于点D,若∠ADC=105°,BC=CD=3,则AD的值为 ( )
A.3
B.2
C.
D.
6.如图,点B在☉A上,点C在☉A外,以下条件不能判定BC是☉A的切线的是 ( )
A.∠A=50°,∠C=40°
B.∠B-∠C=∠A
C.AB2+BC2=AC2
D.☉A与AC的交点是AC中点
7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是 ( )
A.点(0,3) B.点(1,3)
C.点(6,0) D.点(6,1)
8.下列命题正确的是 ( )
A.矩形为正多边形
B.圆内接的菱形一定是正方形
C.正多边形都是中心对称图形
D.正多边形一定既是轴对称图形,又是中心对称图形
9.正八边形的每个内角为 ( )
A.120° B.135° C.140° D.144°
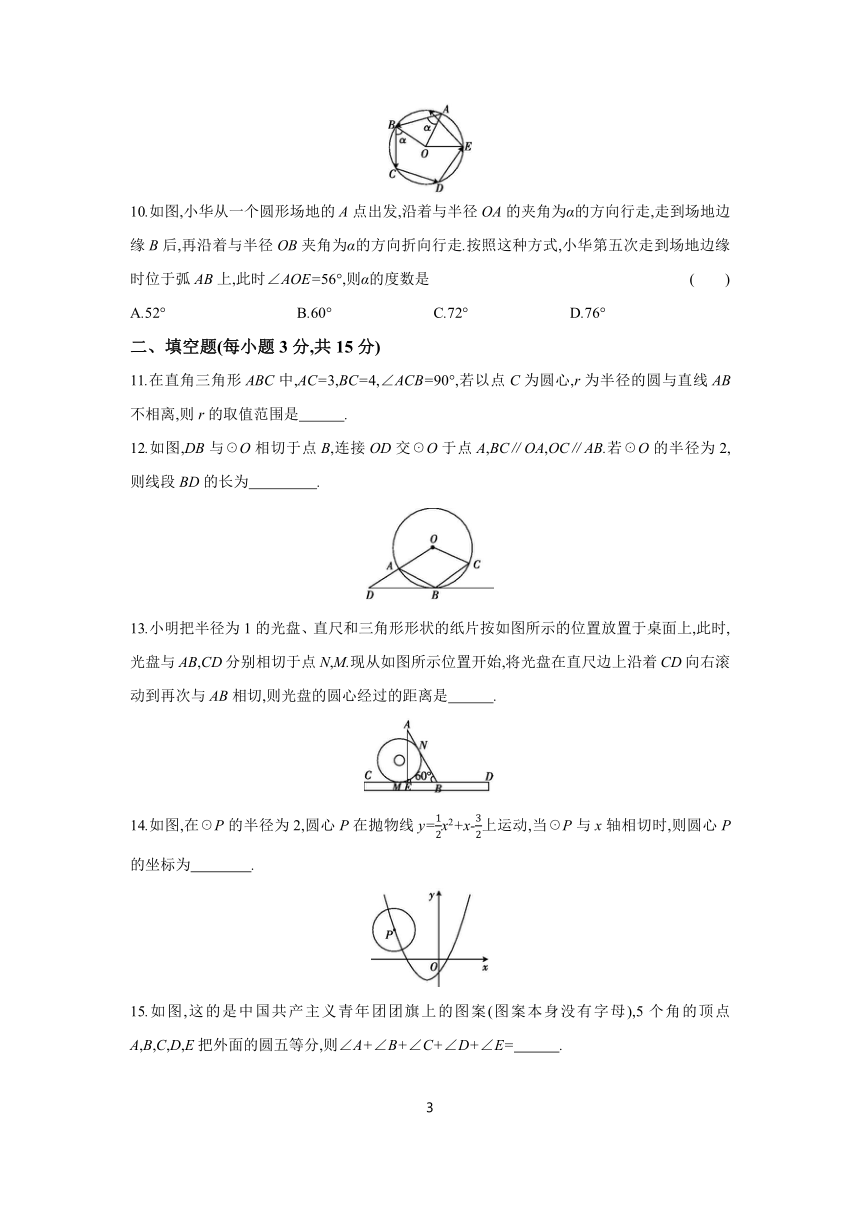
10.如图,小华从一个圆形场地的A点出发,沿着与半径OA的夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时位于弧AB上,此时∠AOE=56°,则α的度数是 ( )
A.52° B.60° C.72° D.76°
二、填空题(每小题3分,共15分)
11.在直角三角形ABC中,AC=3,BC=4,∠ACB=90°,若以点C为圆心,r为半径的圆与直线AB不相离,则r的取值范围是 .
12.如图,DB与☉O相切于点B,连接OD交☉O于点A,BC∥OA,OC∥AB.若☉O的半径为2,则线段BD的长为 .
13.小明把半径为1的光盘、直尺和三角形形状的纸片按如图所示的位置放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切,则光盘的圆心经过的距离是 .
14.如图,在☉P的半径为2,圆心P在抛物线y=x2+x-上运动,当☉P与x轴相切时,则圆心P的坐标为 .
15.如图,这的是中国共产主义青年团团旗上的图案(图案本身没有字母),5个角的顶点A,B,C,D,E把外面的圆五等分,则∠A+∠B+∠C+∠D+∠E= .
三、解答题(共55分)
16.(10分)如图,已知Rt△ABC中,∠ABC=90°,以BC为直径的☉O与斜边AC交于D点,DE为☉O的切线,DE⊥CE,且DE=AD.
(1)求证:△DCE≌△ABD.
(2)若CD=2,求DE的长.
17.(10分)如图,AB是☉O的直径,BD是☉O的弦,延长BD到点C,使DC=BD,连接AC,E为AC上一点,直线ED与AB的延长线交于点F,若∠CDE=∠DAC,AC=12.
(1)求☉O半径.
(2)求证:DE为☉O的切线.
18.(11分)如图,在△ABC中,点I是△ABC的内心(三角形三条角平分线的交点),延长AI与△ABC的外接圆交于点D,连接BD,DC.
(1)求证:DI=DB.
(2)若∠BAC=60°,BC=2,求DI的长.
19.(12分)如图,在 ABCD中,过A,B,D三点的☉O交BC于点E,连接DE,∠CDE=∠DAE.
(1)求证:DE=AB.
(2)判断直线DC与☉O的位置关系,并说明理由.
(3)若AB=3,AE=6,求CE的长.
20.(12分)如图,在△ABC中,∠BAC=90°.BM平分∠ABC交AC于点M,以A为圆心,AM的长为半径作☉A交BM于点N,AN的延长线交BC于点D,直线AB交☉A于P,K两点,作MT⊥BC于点T.求证:
(1)AK=MT.
(2)AD⊥BC.
(3)当AK=BD时,=.
参考答案
1.A 2.B 3.B 4.D 5.A 6.D 7.B 8.B 9.B
10.A 11.r≥2.5 12.2 13.
14.(-1+2,2)或(-1-2,2)或(-1,-2)
15.180°
16.【解析】
(1)证明:如图,连接OD.
∵ED是☉O的切线,∴OD⊥DE.
又∵CE⊥DE,∴OD∥CE,∴∠ECD=∠CDO.
又∵OC=OD,
∴∠ODC=∠OCD.
∵BC为☉O的直径,∠ABC=90°,
∴∠ABD=∠ACB,∴∠ABD=∠ECD.
又∵DE=AD,∠E=∠ADB=90°,
∴△DCE≌△ABD(AAS).
(2)由(1)可知,CD=AB=2,设ED=x,则AD=x,由=,可得=,
解得x=-1或x=--1(不合题意,舍去),
故DE的长是-1.
17.【解析】(1)∵AB为☉O的直径,
∴∠ADB=90°,∴AD⊥BC.
又∵BD=CD,∴AB=AC=12,
∴☉O半径为6.
(2)证明:如图,连接OD.
∵∠CDE=∠DAC,
∴∠CDE+∠C=∠DAC+∠C,
∴∠AED=∠ADB.
由(1)知∠ADB=90°,
∴∠AED=90°.
∵DC=BD,OA=OB,
∴OD∥AC,∴∠ODF=∠AED=90°,
∴半径OD⊥EF,∴DE为☉O的切线.
18.【解析】(1)证明:如图,连接BI.
∵点I是△ABC的内心,
∴AD平分∠BAC,BI平分∠ABC,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠BID=∠BAI+∠IBA,∠IBD=∠CBI+∠CBD,∠CBD=∠CAD,
∴∠BID=∠IBD,∴DI=DB.
(2)如图,过点D作DE⊥BC于点E.
由(1)得∠BAD=∠CAD,
∴=,∴BD=CD.
∵DE⊥BC,∴BE=CE=BC=.
∵∠BAC=60°,∴∠BAD=∠CAD=30°,
∴∠DBC=∠BCD=30°,
∴DE=BE=1,BD=2DE=2,
∴DI=BD=2.
19.【解析】(1)证明:在 ABCD中,AD∥BC,
∴∠DAE=∠AEB,
∴=,DE=AB.
(2)直线DC与☉O相切.
理由:如图,作直径DF,连接AF,于是有∠EAF=∠EDF.
∵∠DAE=∠CDE,
∴∠EAF+∠DAE=∠EDF+∠CDE,即∠DAF=∠CDF.
∵DF是☉O的直径,点A在☉O上,
∴∠DAF=90°,∴∠CDF=90°,
∴OD⊥CD.
∵直线DC经过☉O半径OD外端D,且与半径垂直,
∴直线DC与☉O相切.
(3)由(1)可知∠EDA=∠DAB.
在 ABCD中,∠DAB=∠DCB,
∴∠EDA=∠DCB.又∵∠DAE=∠CDE,
∴△ADE∽△DCE,
∴=.
∵AB=3,由(1)得AB=DE=DC=3,
即=,
解得CE=.
20.【解析】证明:(1)∵BM平分∠ABC,∠BAC=90°,MT⊥BC,
∴AM=MT.又∵AM=AK,∴AK=MT.
(2)∵BM平分∠ABC,
∴∠ABM=∠CBM.
∵AM=AN,∴∠AMN=∠ANM.
又∵∠ANM=∠BND,∴∠AMN=∠BND.
∵∠BAC=90°,∴∠ABM+∠AMB=90°,
∴∠CBM+∠BND=90°,∴∠BDN=90°,
∴AD⊥BC.
(3)如图,连接PN,KM,易证△BPN∽△BMK,∴=.
∵AK=BD,AK=MT,∴BD=MT.
∵AD⊥BC,MT⊥BC,∴∠ADB=∠MTC=90°,
∴∠C+∠CMT=90°.
∵∠BAC=90°,∴∠C+∠ABC=90°,
∴∠ABC=∠CMT.
在△ABD和△CMT中,
∴△ABD≌△CMT,∴AB=MC.
∵AK=AM,
∴AB+AK=MC+AM,即BK=AC,
∴=.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共30分)
1.若☉O的半径为6,点O到直线l的距离为3,则下列图中位置关系正确的是 ( )
2.在平面直角坐标系中,以(-2,3)为圆心,3为半径的圆一定 ( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
3.如图,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C.若AB=8,OA=6,则BC的长为 ( )
A.3 B.4 C.5 D.6
4.如图,AB是半圆O的直径,C是BA延长线上一点,CD切半圆O于点E,BD⊥CD于点D,若CD=8,BD=6,则半圆O的半径为 ( )
A.3.5 B.4 C.2 D.3.75
5.如图,经过A,C两点的☉O与△ABC的边BC相切,与边AB交于点D,若∠ADC=105°,BC=CD=3,则AD的值为 ( )
A.3
B.2
C.
D.
6.如图,点B在☉A上,点C在☉A外,以下条件不能判定BC是☉A的切线的是 ( )
A.∠A=50°,∠C=40°
B.∠B-∠C=∠A
C.AB2+BC2=AC2
D.☉A与AC的交点是AC中点
7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是 ( )
A.点(0,3) B.点(1,3)
C.点(6,0) D.点(6,1)
8.下列命题正确的是 ( )
A.矩形为正多边形
B.圆内接的菱形一定是正方形
C.正多边形都是中心对称图形
D.正多边形一定既是轴对称图形,又是中心对称图形
9.正八边形的每个内角为 ( )
A.120° B.135° C.140° D.144°
10.如图,小华从一个圆形场地的A点出发,沿着与半径OA的夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时位于弧AB上,此时∠AOE=56°,则α的度数是 ( )
A.52° B.60° C.72° D.76°
二、填空题(每小题3分,共15分)
11.在直角三角形ABC中,AC=3,BC=4,∠ACB=90°,若以点C为圆心,r为半径的圆与直线AB不相离,则r的取值范围是 .
12.如图,DB与☉O相切于点B,连接OD交☉O于点A,BC∥OA,OC∥AB.若☉O的半径为2,则线段BD的长为 .
13.小明把半径为1的光盘、直尺和三角形形状的纸片按如图所示的位置放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切,则光盘的圆心经过的距离是 .
14.如图,在☉P的半径为2,圆心P在抛物线y=x2+x-上运动,当☉P与x轴相切时,则圆心P的坐标为 .
15.如图,这的是中国共产主义青年团团旗上的图案(图案本身没有字母),5个角的顶点A,B,C,D,E把外面的圆五等分,则∠A+∠B+∠C+∠D+∠E= .
三、解答题(共55分)
16.(10分)如图,已知Rt△ABC中,∠ABC=90°,以BC为直径的☉O与斜边AC交于D点,DE为☉O的切线,DE⊥CE,且DE=AD.
(1)求证:△DCE≌△ABD.
(2)若CD=2,求DE的长.
17.(10分)如图,AB是☉O的直径,BD是☉O的弦,延长BD到点C,使DC=BD,连接AC,E为AC上一点,直线ED与AB的延长线交于点F,若∠CDE=∠DAC,AC=12.
(1)求☉O半径.
(2)求证:DE为☉O的切线.
18.(11分)如图,在△ABC中,点I是△ABC的内心(三角形三条角平分线的交点),延长AI与△ABC的外接圆交于点D,连接BD,DC.
(1)求证:DI=DB.
(2)若∠BAC=60°,BC=2,求DI的长.
19.(12分)如图,在 ABCD中,过A,B,D三点的☉O交BC于点E,连接DE,∠CDE=∠DAE.
(1)求证:DE=AB.
(2)判断直线DC与☉O的位置关系,并说明理由.
(3)若AB=3,AE=6,求CE的长.
20.(12分)如图,在△ABC中,∠BAC=90°.BM平分∠ABC交AC于点M,以A为圆心,AM的长为半径作☉A交BM于点N,AN的延长线交BC于点D,直线AB交☉A于P,K两点,作MT⊥BC于点T.求证:
(1)AK=MT.
(2)AD⊥BC.
(3)当AK=BD时,=.
参考答案
1.A 2.B 3.B 4.D 5.A 6.D 7.B 8.B 9.B
10.A 11.r≥2.5 12.2 13.
14.(-1+2,2)或(-1-2,2)或(-1,-2)
15.180°
16.【解析】
(1)证明:如图,连接OD.
∵ED是☉O的切线,∴OD⊥DE.
又∵CE⊥DE,∴OD∥CE,∴∠ECD=∠CDO.
又∵OC=OD,
∴∠ODC=∠OCD.
∵BC为☉O的直径,∠ABC=90°,
∴∠ABD=∠ACB,∴∠ABD=∠ECD.
又∵DE=AD,∠E=∠ADB=90°,
∴△DCE≌△ABD(AAS).
(2)由(1)可知,CD=AB=2,设ED=x,则AD=x,由=,可得=,
解得x=-1或x=--1(不合题意,舍去),
故DE的长是-1.
17.【解析】(1)∵AB为☉O的直径,
∴∠ADB=90°,∴AD⊥BC.
又∵BD=CD,∴AB=AC=12,
∴☉O半径为6.
(2)证明:如图,连接OD.
∵∠CDE=∠DAC,
∴∠CDE+∠C=∠DAC+∠C,
∴∠AED=∠ADB.
由(1)知∠ADB=90°,
∴∠AED=90°.
∵DC=BD,OA=OB,
∴OD∥AC,∴∠ODF=∠AED=90°,
∴半径OD⊥EF,∴DE为☉O的切线.
18.【解析】(1)证明:如图,连接BI.
∵点I是△ABC的内心,
∴AD平分∠BAC,BI平分∠ABC,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠BID=∠BAI+∠IBA,∠IBD=∠CBI+∠CBD,∠CBD=∠CAD,
∴∠BID=∠IBD,∴DI=DB.
(2)如图,过点D作DE⊥BC于点E.
由(1)得∠BAD=∠CAD,
∴=,∴BD=CD.
∵DE⊥BC,∴BE=CE=BC=.
∵∠BAC=60°,∴∠BAD=∠CAD=30°,
∴∠DBC=∠BCD=30°,
∴DE=BE=1,BD=2DE=2,
∴DI=BD=2.
19.【解析】(1)证明:在 ABCD中,AD∥BC,
∴∠DAE=∠AEB,
∴=,DE=AB.
(2)直线DC与☉O相切.
理由:如图,作直径DF,连接AF,于是有∠EAF=∠EDF.
∵∠DAE=∠CDE,
∴∠EAF+∠DAE=∠EDF+∠CDE,即∠DAF=∠CDF.
∵DF是☉O的直径,点A在☉O上,
∴∠DAF=90°,∴∠CDF=90°,
∴OD⊥CD.
∵直线DC经过☉O半径OD外端D,且与半径垂直,
∴直线DC与☉O相切.
(3)由(1)可知∠EDA=∠DAB.
在 ABCD中,∠DAB=∠DCB,
∴∠EDA=∠DCB.又∵∠DAE=∠CDE,
∴△ADE∽△DCE,
∴=.
∵AB=3,由(1)得AB=DE=DC=3,
即=,
解得CE=.
20.【解析】证明:(1)∵BM平分∠ABC,∠BAC=90°,MT⊥BC,
∴AM=MT.又∵AM=AK,∴AK=MT.
(2)∵BM平分∠ABC,
∴∠ABM=∠CBM.
∵AM=AN,∴∠AMN=∠ANM.
又∵∠ANM=∠BND,∴∠AMN=∠BND.
∵∠BAC=90°,∴∠ABM+∠AMB=90°,
∴∠CBM+∠BND=90°,∴∠BDN=90°,
∴AD⊥BC.
(3)如图,连接PN,KM,易证△BPN∽△BMK,∴=.
∵AK=BD,AK=MT,∴BD=MT.
∵AD⊥BC,MT⊥BC,∴∠ADB=∠MTC=90°,
∴∠C+∠CMT=90°.
∵∠BAC=90°,∴∠C+∠ABC=90°,
∴∠ABC=∠CMT.
在△ABD和△CMT中,
∴△ABD≌△CMT,∴AB=MC.
∵AK=AM,
∴AB+AK=MC+AM,即BK=AC,
∴=.
2
