第30章 二次函数 单元测试(含答案) 2023-2024学年初中数学冀教版九年级下册
文档属性
| 名称 | 第30章 二次函数 单元测试(含答案) 2023-2024学年初中数学冀教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览



文档简介
第三十章 二次函数 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共18分)
1.抛物线y=-(x+1)2-2的对称轴是 ( )
A.直线x=1 B.直线x=-1
C.直线x=2 D.直线x=-2
2.据省统计局公布的数据,合肥市一月地区生产总值约为6百亿元人民币,若合肥市三月地区生产总值为y百亿元人民币,平均每个月地区生产总值增长的百分率为x,则y关于x的函数表达式是 ( )
A.y=6(1+2x)
B.y=6(1-x)2
C.y=6(1+x)2
D.y=6+6(1+x)+6(1+x)2
3.下列关于二次函数y=3(x-4)2-2的说法正确的是 ( )
A.其图像的开口向下
B.其图像的对称轴为直线x=4
C.其图像的顶点坐标为(4,2)
D.当x>3时,y随x的增大而增大
4.若二次函数y=ax2+bx+c的部分图像如图所示,则关于x的方程ax2+bx+c=0的解是 ( )
A.x=1
B.x=-3
C.x1=1,x2=-3
D.x1=-1,x2=-2
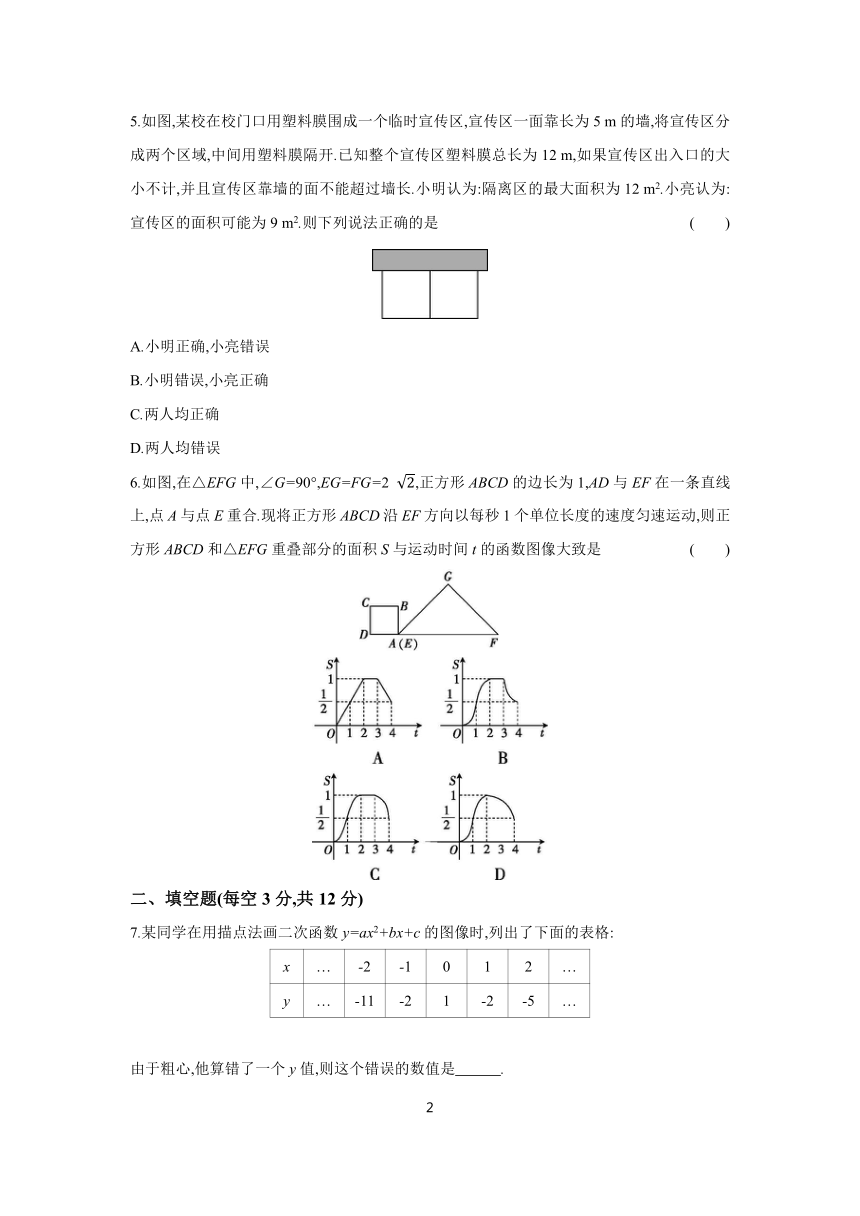
5.如图,某校在校门口用塑料膜围成一个临时宣传区,宣传区一面靠长为5 m的墙,将宣传区分成两个区域,中间用塑料膜隔开.已知整个宣传区塑料膜总长为12 m,如果宣传区出入口的大小不计,并且宣传区靠墙的面不能超过墙长.小明认为:隔离区的最大面积为12 m2.小亮认为:宣传区的面积可能为9 m2.则下列说法正确的是 ( )
A.小明正确,小亮错误
B.小明错误,小亮正确
C.两人均正确
D.两人均错误
6.如图,在△EFG中,∠G=90°,EG=FG=2 ,正方形ABCD的边长为1,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位长度的速度匀速运动,则正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图像大致是 ( )
二、填空题(每空3分,共12分)
7.某同学在用描点法画二次函数y=ax2+bx+c的图像时,列出了下面的表格:
x … -2 -1 0 1 2 …
y … -11 -2 1 -2 -5 …
由于粗心,他算错了一个y值,则这个错误的数值是 .
8.定义:一次函数y=ax+b的特征数是[a,b].若一次函数y=-2x+m的图像向下平移3个单位长度后与反比例函数y=的图像相交,其中一个交点A的坐标为(n,-4),则一次函数y=-2x+m的特征数是 .
9.已知y关于x的函数表达式为y=
(1)当y随x的增大而减小时,x的取值范围是 .
(2)若当y=k时,对应自变量x的值有3个,则k的取值范围是 .
三、解答题(共70分)
10.(8分)已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,3)三点.
(1)求这条抛物线的表达式.
(2)写出这条抛物线的开口方向、对称轴和顶点坐标.
11.(8分)【2022 石家庄期末】在校园嘉年华中,九年级同学将对一块长为20 m、宽为10 m的场地进行布置,设计方案如图所示.阴影区域为绿化区(四块全等的矩形),空白区域为活动区,且4个出口宽度相同,其宽度不小于4 m,不大于8 m.设出口长均为x(m),活动区面积为y(m2).
(1)y关于x的函数表达式为 .
(2)当x= 时,活动区面积最大,此时活动区的面积是 m2.
(3)若活动区布置成本为10元/m2,绿化区布置成本为8元/m2,布置场地的预算不超过1850元,x为整数,当x= 时,符合预算且使活动区面积最大,此时布置场地所需的费用为 元.
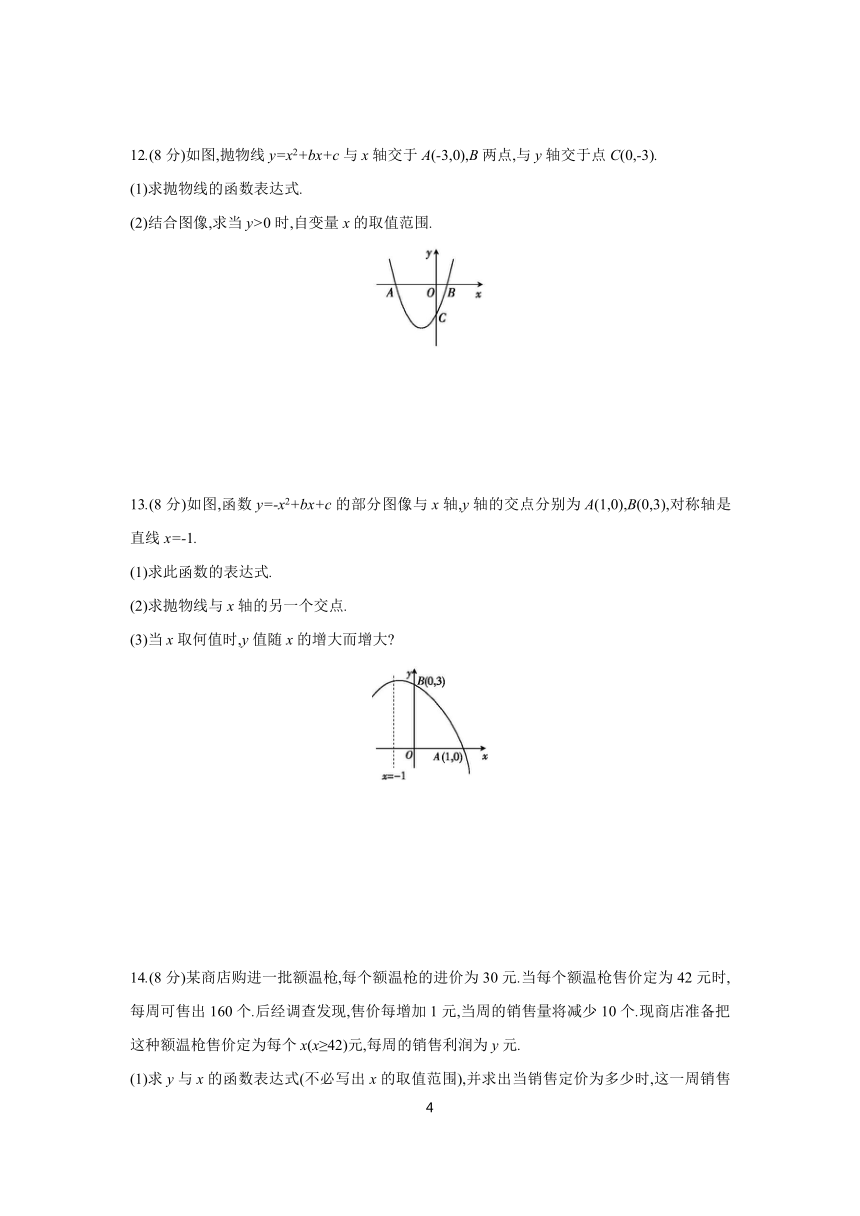
12.(8分)如图,抛物线y=x2+bx+c与x轴交于A(-3,0),B两点,与y轴交于点C(0,-3).
(1)求抛物线的函数表达式.
(2)结合图像,求当y>0时,自变量x的取值范围.
13.(8分)如图,函数y=-x2+bx+c的部分图像与x轴,y轴的交点分别为A(1,0),B(0,3),对称轴是直线x=-1.
(1)求此函数的表达式.
(2)求抛物线与x轴的另一个交点.
(3)当x取何值时,y值随x的增大而增大
14.(8分)某商店购进一批额温枪,每个额温枪的进价为30元.当每个额温枪售价定为42元时,每周可售出160个.后经调查发现,售价每增加1元,当周的销售量将减少10个.现商店准备把这种额温枪售价定为每个x(x≥42)元,每周的销售利润为y元.
(1)求y与x的函数表达式(不必写出x的取值范围),并求出当销售定价为多少时,这一周销售额温枪的利润最大.
(2)若该商店在某周销售这种额温枪的利润为1600元,求该周这种额温枪的销售单价.
15.(10分)【保定期末】如图,在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图像与x轴交于A,B两点,B点坐标为(3,0),与y轴交于点C(0,-3).
(1)求这个二次函数的表达式.
(2)设这个二次函数的图像的顶点为M,求△ABM的面积.
(3)若方程x2+bx+c=k有两个不相等的实数根,则k的取值范围是 .
16.(10分)已知抛物线y=(x-m)2-2(m-1)2和直线y=mx,其中m为常数,且m≥1.
(1)若该抛物线的顶点在x轴上.
①求m的值;
②若直线y=mx与抛物线相交于M,N两点,P为线段MN上一动点,过点P作x轴的垂线交抛物线于点Q,求线段PQ长的最大值.
(2)若直线y=mx与抛物线相交于A,B两点(点B在对称轴的右边),且与抛物线的对称轴相交于C点,当CO=CB时,求抛物线的顶点坐标.
17.(10分)【2021河北中考】如图,这是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴的距离OK=10.从点A处向右上方沿抛物线L:y=-x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,在图中补画出y轴,并直接指出点P会落在哪个台阶上.
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的表达式,并说明其对称轴是否与台阶T5有交点.(不必写x的取值范围)
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少
参考答案
1.B 2.C 3.B 4.C 5.B 6.C
7.-5 8.[-2,-13] 9.(1)x≤1或x>2 (2)210.【解析】(1)将点(-1,0),(0,-3),(2,3)代入表达式得
解得
∴这条抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2x-2-,
∴这条抛物线的开口向上,对称轴为直线x=,顶点坐标为.
11.(1)y=-x2+30x(4≤x≤8) (2)8 176 (3)5 1850
【解析】(1)由题意,得y=20×10-4××=-x2+30x,∴y关于x的函数表达式为y=-x2+30x(4≤x≤8).
(2)∵y=-x2+30x=-(x-15)2+225,x的取值范围是4≤x≤8,∴当x=8时,函数y=-(x-15)2+225取得最大值,最大值为176.
(3)设布置场地所需的费用为z元,则z=10(-x2+30x)+8[200-(-x2+30x)]=-2x2+60x+1600,将z=1850代入z=-2x2+60x+1600,得-2x2+60x+1600=1850,解得x=25或x=5,∴当布置场地的预算不超过1850元时,x≤5或x≥25.∵4≤x≤8,∴4≤x≤5.∵活动区域面积为y=-x2+30x,-1<0,对称轴为直线x=15,∴当x=5时,活动区面积最大,此时布置场地所需的费用为1850元.
12.【解析】(1)由抛物线y=x2+bx+c经过点A(-3,0),C(0,-3),
得
解得
∴抛物线的表达式为y=x2+2x-3.
(2)由(1)知y=x2+2x-3,
令y=0,则x2+2x-3=0,
解得x1=-3,x2=1,
∴点B的坐标为(1,0).
∵A(-3,0),B(1,0),
∴由图可知,当y>0时,自变量x的取值范围为x<-3或x>1.
13.【解析】(1)将A(1,0),B(0,3)分别代入表达式,得解得则此函数的表达式为y=-x2-2x+3.
(2)当y=0时,-x2-2x+3=0,
解得x1=-3,x2=1.
所以抛物线与x轴的另一个交点是(-3,0).
(3)由图可知,当x<-1 时,y随x 的增大而增大.
14.【解析】(1)根据题意知y=(x-30)[160-(x-42)×10],
整理得y=-10x2+880x-17400,
化为顶点式,得y=-10(x-44)2+1960.
∵-10<0,
∴当x=44时,y有最大值,最大值为1960,
∴当销售定价为44元时,这周销售额温枪的利润最大.
(2)当y=1600时,代入y=-10(x-44)2+1960中,
得-10(x-44)2+1960=1600,
解得x=50或x=38(不符合题意,舍去).
答:当该商店在某周销售这种额温枪的利润为1600元时,其销售单价为50元.
15.【解析】(1)分别把B(3,0),C(0,-3)代入y=x2+bx+c,得解得
∴二次函数的表达式为y=x2-2x-3.
(2)在y=x2-2x-3中,令y=0,
得x2-2x-3=0,解得x1=-1,x2=3,∴AB=4.
∵y=x2-2x-3=(x-1)2-4,∴顶点M(1,-4),
∴S△ABM=×4×4=8.
(3)k>-4.
16.【解析】(1)①∵抛物线y=(x-m)2-2(m-1)2的顶点在x轴上,
∴-2(m-1)2=0,
解得m=1.
②如图1,
图1
由m=1知抛物线为y=(x-1)2=x2-2x+1,直线为y=x,
设P,则Q,
∴PQ=t-(t2-2t+1)=-t2+t-1=-+.
∵-1<0,
∴当t=时,PQ的长取最大值,最大值为.
(2)如图2,设抛物线对称轴交x轴于点D,过点C作CE∥x轴,过点B作BE∥CD交CE于点E.
图2
设A(xA,yA),B(xB,yB).
∵抛物线y=(x-m)2-2(m-1)2的对称轴为直线x=m,顶点坐标为(m,-2(m-1)2),
∴点C的横坐标xC=m.
∵CO=CB,∠CDO=90°=∠BEC,∠BCE=∠COD,
∴△COD≌△BCE(AAS),
∴DO=EC,即xB-m=m-0,
∴xB=2m①,
由
得x2-mx-m2+4m-2=0,
∴xA+xB=m②,xA·xB=-m2+4m-2③,
由②得xA=m-xB④,
把①④代入③得m-2m×2m=-m2+4m-2,
解得m=2或m=.
当m=2时,-2(m-1)2=-2×(2-1)2=-2,
∴此时抛物线的顶点坐标为(2,-2);
当m=时,-2(m-1)2=-2×=-,
∴此时抛物线的顶点坐标为.
综上所述,抛物线的顶点坐标为(2,-2)或.
17.【解析】(1)当y=0时,-x2+4x+12=0,
解得x1=-2,x2=6,
由题意知点A为L与x轴的左交点,
∴点A的横坐标为-2.
y轴如图所示.
点P会落在台阶T4上.
(2)由题意,设抛物线C的表达式为 y=-(x-h)2+11.
计算易得点P落在T4上的点(5,7)处,
把x=5,y=7代入y=-(x-h)2+11,
得7=-(5-h)2+11,解得h1=7,h2=3,
由题意可知h>5,∴h=7,
∴抛物线C的表达式为 y=-(x-7)2+11.
易知抛物线C的对称轴为直线x=7,
∵6<7<7.5,∴该对称轴与台阶T5有交点.
(3)由(2)知当点P落在B,D处时,其横坐标x>7,
对于y=-(x-7)2+11,
当 y=2时,2=-(x-7)2+11,解得x1=10,x2=4,
∴点P落在点B时,xB=10;
当 y=0时,0=-(x-7)2+11,解得 x1=7+,x2=7-(舍去),
∴点P落在点D时,xD=7+,
∴点B横坐标的最大值比最小值大(7++1)-10=-2.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共18分)
1.抛物线y=-(x+1)2-2的对称轴是 ( )
A.直线x=1 B.直线x=-1
C.直线x=2 D.直线x=-2
2.据省统计局公布的数据,合肥市一月地区生产总值约为6百亿元人民币,若合肥市三月地区生产总值为y百亿元人民币,平均每个月地区生产总值增长的百分率为x,则y关于x的函数表达式是 ( )
A.y=6(1+2x)
B.y=6(1-x)2
C.y=6(1+x)2
D.y=6+6(1+x)+6(1+x)2
3.下列关于二次函数y=3(x-4)2-2的说法正确的是 ( )
A.其图像的开口向下
B.其图像的对称轴为直线x=4
C.其图像的顶点坐标为(4,2)
D.当x>3时,y随x的增大而增大
4.若二次函数y=ax2+bx+c的部分图像如图所示,则关于x的方程ax2+bx+c=0的解是 ( )
A.x=1
B.x=-3
C.x1=1,x2=-3
D.x1=-1,x2=-2
5.如图,某校在校门口用塑料膜围成一个临时宣传区,宣传区一面靠长为5 m的墙,将宣传区分成两个区域,中间用塑料膜隔开.已知整个宣传区塑料膜总长为12 m,如果宣传区出入口的大小不计,并且宣传区靠墙的面不能超过墙长.小明认为:隔离区的最大面积为12 m2.小亮认为:宣传区的面积可能为9 m2.则下列说法正确的是 ( )
A.小明正确,小亮错误
B.小明错误,小亮正确
C.两人均正确
D.两人均错误
6.如图,在△EFG中,∠G=90°,EG=FG=2 ,正方形ABCD的边长为1,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位长度的速度匀速运动,则正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图像大致是 ( )
二、填空题(每空3分,共12分)
7.某同学在用描点法画二次函数y=ax2+bx+c的图像时,列出了下面的表格:
x … -2 -1 0 1 2 …
y … -11 -2 1 -2 -5 …
由于粗心,他算错了一个y值,则这个错误的数值是 .
8.定义:一次函数y=ax+b的特征数是[a,b].若一次函数y=-2x+m的图像向下平移3个单位长度后与反比例函数y=的图像相交,其中一个交点A的坐标为(n,-4),则一次函数y=-2x+m的特征数是 .
9.已知y关于x的函数表达式为y=
(1)当y随x的增大而减小时,x的取值范围是 .
(2)若当y=k时,对应自变量x的值有3个,则k的取值范围是 .
三、解答题(共70分)
10.(8分)已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,3)三点.
(1)求这条抛物线的表达式.
(2)写出这条抛物线的开口方向、对称轴和顶点坐标.
11.(8分)【2022 石家庄期末】在校园嘉年华中,九年级同学将对一块长为20 m、宽为10 m的场地进行布置,设计方案如图所示.阴影区域为绿化区(四块全等的矩形),空白区域为活动区,且4个出口宽度相同,其宽度不小于4 m,不大于8 m.设出口长均为x(m),活动区面积为y(m2).
(1)y关于x的函数表达式为 .
(2)当x= 时,活动区面积最大,此时活动区的面积是 m2.
(3)若活动区布置成本为10元/m2,绿化区布置成本为8元/m2,布置场地的预算不超过1850元,x为整数,当x= 时,符合预算且使活动区面积最大,此时布置场地所需的费用为 元.
12.(8分)如图,抛物线y=x2+bx+c与x轴交于A(-3,0),B两点,与y轴交于点C(0,-3).
(1)求抛物线的函数表达式.
(2)结合图像,求当y>0时,自变量x的取值范围.
13.(8分)如图,函数y=-x2+bx+c的部分图像与x轴,y轴的交点分别为A(1,0),B(0,3),对称轴是直线x=-1.
(1)求此函数的表达式.
(2)求抛物线与x轴的另一个交点.
(3)当x取何值时,y值随x的增大而增大
14.(8分)某商店购进一批额温枪,每个额温枪的进价为30元.当每个额温枪售价定为42元时,每周可售出160个.后经调查发现,售价每增加1元,当周的销售量将减少10个.现商店准备把这种额温枪售价定为每个x(x≥42)元,每周的销售利润为y元.
(1)求y与x的函数表达式(不必写出x的取值范围),并求出当销售定价为多少时,这一周销售额温枪的利润最大.
(2)若该商店在某周销售这种额温枪的利润为1600元,求该周这种额温枪的销售单价.
15.(10分)【保定期末】如图,在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图像与x轴交于A,B两点,B点坐标为(3,0),与y轴交于点C(0,-3).
(1)求这个二次函数的表达式.
(2)设这个二次函数的图像的顶点为M,求△ABM的面积.
(3)若方程x2+bx+c=k有两个不相等的实数根,则k的取值范围是 .
16.(10分)已知抛物线y=(x-m)2-2(m-1)2和直线y=mx,其中m为常数,且m≥1.
(1)若该抛物线的顶点在x轴上.
①求m的值;
②若直线y=mx与抛物线相交于M,N两点,P为线段MN上一动点,过点P作x轴的垂线交抛物线于点Q,求线段PQ长的最大值.
(2)若直线y=mx与抛物线相交于A,B两点(点B在对称轴的右边),且与抛物线的对称轴相交于C点,当CO=CB时,求抛物线的顶点坐标.
17.(10分)【2021河北中考】如图,这是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴的距离OK=10.从点A处向右上方沿抛物线L:y=-x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,在图中补画出y轴,并直接指出点P会落在哪个台阶上.
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的表达式,并说明其对称轴是否与台阶T5有交点.(不必写x的取值范围)
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少
参考答案
1.B 2.C 3.B 4.C 5.B 6.C
7.-5 8.[-2,-13] 9.(1)x≤1或x>2 (2)2
解得
∴这条抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2x-2-,
∴这条抛物线的开口向上,对称轴为直线x=,顶点坐标为.
11.(1)y=-x2+30x(4≤x≤8) (2)8 176 (3)5 1850
【解析】(1)由题意,得y=20×10-4××=-x2+30x,∴y关于x的函数表达式为y=-x2+30x(4≤x≤8).
(2)∵y=-x2+30x=-(x-15)2+225,x的取值范围是4≤x≤8,∴当x=8时,函数y=-(x-15)2+225取得最大值,最大值为176.
(3)设布置场地所需的费用为z元,则z=10(-x2+30x)+8[200-(-x2+30x)]=-2x2+60x+1600,将z=1850代入z=-2x2+60x+1600,得-2x2+60x+1600=1850,解得x=25或x=5,∴当布置场地的预算不超过1850元时,x≤5或x≥25.∵4≤x≤8,∴4≤x≤5.∵活动区域面积为y=-x2+30x,-1<0,对称轴为直线x=15,∴当x=5时,活动区面积最大,此时布置场地所需的费用为1850元.
12.【解析】(1)由抛物线y=x2+bx+c经过点A(-3,0),C(0,-3),
得
解得
∴抛物线的表达式为y=x2+2x-3.
(2)由(1)知y=x2+2x-3,
令y=0,则x2+2x-3=0,
解得x1=-3,x2=1,
∴点B的坐标为(1,0).
∵A(-3,0),B(1,0),
∴由图可知,当y>0时,自变量x的取值范围为x<-3或x>1.
13.【解析】(1)将A(1,0),B(0,3)分别代入表达式,得解得则此函数的表达式为y=-x2-2x+3.
(2)当y=0时,-x2-2x+3=0,
解得x1=-3,x2=1.
所以抛物线与x轴的另一个交点是(-3,0).
(3)由图可知,当x<-1 时,y随x 的增大而增大.
14.【解析】(1)根据题意知y=(x-30)[160-(x-42)×10],
整理得y=-10x2+880x-17400,
化为顶点式,得y=-10(x-44)2+1960.
∵-10<0,
∴当x=44时,y有最大值,最大值为1960,
∴当销售定价为44元时,这周销售额温枪的利润最大.
(2)当y=1600时,代入y=-10(x-44)2+1960中,
得-10(x-44)2+1960=1600,
解得x=50或x=38(不符合题意,舍去).
答:当该商店在某周销售这种额温枪的利润为1600元时,其销售单价为50元.
15.【解析】(1)分别把B(3,0),C(0,-3)代入y=x2+bx+c,得解得
∴二次函数的表达式为y=x2-2x-3.
(2)在y=x2-2x-3中,令y=0,
得x2-2x-3=0,解得x1=-1,x2=3,∴AB=4.
∵y=x2-2x-3=(x-1)2-4,∴顶点M(1,-4),
∴S△ABM=×4×4=8.
(3)k>-4.
16.【解析】(1)①∵抛物线y=(x-m)2-2(m-1)2的顶点在x轴上,
∴-2(m-1)2=0,
解得m=1.
②如图1,
图1
由m=1知抛物线为y=(x-1)2=x2-2x+1,直线为y=x,
设P,则Q,
∴PQ=t-(t2-2t+1)=-t2+t-1=-+.
∵-1<0,
∴当t=时,PQ的长取最大值,最大值为.
(2)如图2,设抛物线对称轴交x轴于点D,过点C作CE∥x轴,过点B作BE∥CD交CE于点E.
图2
设A(xA,yA),B(xB,yB).
∵抛物线y=(x-m)2-2(m-1)2的对称轴为直线x=m,顶点坐标为(m,-2(m-1)2),
∴点C的横坐标xC=m.
∵CO=CB,∠CDO=90°=∠BEC,∠BCE=∠COD,
∴△COD≌△BCE(AAS),
∴DO=EC,即xB-m=m-0,
∴xB=2m①,
由
得x2-mx-m2+4m-2=0,
∴xA+xB=m②,xA·xB=-m2+4m-2③,
由②得xA=m-xB④,
把①④代入③得m-2m×2m=-m2+4m-2,
解得m=2或m=.
当m=2时,-2(m-1)2=-2×(2-1)2=-2,
∴此时抛物线的顶点坐标为(2,-2);
当m=时,-2(m-1)2=-2×=-,
∴此时抛物线的顶点坐标为.
综上所述,抛物线的顶点坐标为(2,-2)或.
17.【解析】(1)当y=0时,-x2+4x+12=0,
解得x1=-2,x2=6,
由题意知点A为L与x轴的左交点,
∴点A的横坐标为-2.
y轴如图所示.
点P会落在台阶T4上.
(2)由题意,设抛物线C的表达式为 y=-(x-h)2+11.
计算易得点P落在T4上的点(5,7)处,
把x=5,y=7代入y=-(x-h)2+11,
得7=-(5-h)2+11,解得h1=7,h2=3,
由题意可知h>5,∴h=7,
∴抛物线C的表达式为 y=-(x-7)2+11.
易知抛物线C的对称轴为直线x=7,
∵6<7<7.5,∴该对称轴与台阶T5有交点.
(3)由(2)知当点P落在B,D处时,其横坐标x>7,
对于y=-(x-7)2+11,
当 y=2时,2=-(x-7)2+11,解得x1=10,x2=4,
∴点P落在点B时,xB=10;
当 y=0时,0=-(x-7)2+11,解得 x1=7+,x2=7-(舍去),
∴点P落在点D时,xD=7+,
∴点B横坐标的最大值比最小值大(7++1)-10=-2.
2
