第32章 投影与视图单元复习题(含答案) 2023-2024学年初中数学冀教版九年级下册
文档属性
| 名称 | 第32章 投影与视图单元复习题(含答案) 2023-2024学年初中数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 237.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览


文档简介
第三十二章 投影与视图 自我评估
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共24分)
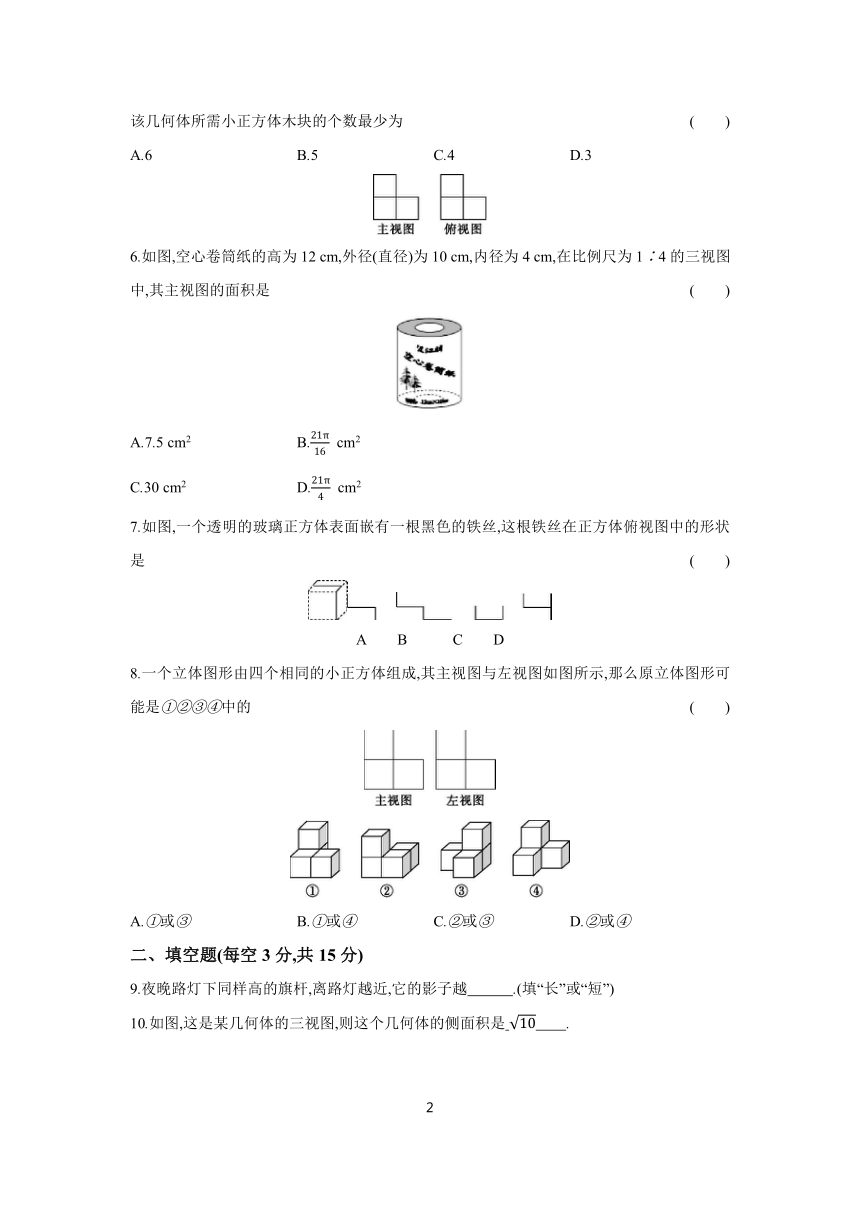
1.下图所示的几何体的左视图是 ( )
A B C D
2.在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等,那么这两根竿子的相对位置是 ( )
A.两竿都垂直于地面
B.两竿平行斜插在地上
C.两根竿子不平行
D.一根竿倒在地上
3.若某物体的三视图如图所示,则该物体的形状可能是 ( )
A.长方体 B.圆锥体 C.正方体 D.圆柱体
4.某正方体的每个面上都有一个汉字,下图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A.厉
B.害
C.了
D.我
5.一个几何体由若干大小相同的小正方体木块搭成,它的主视图和俯视图如图所示,那么搭成该几何体所需小正方体木块的个数最少为 ( )
A.6 B.5 C.4 D.3
6.如图,空心卷筒纸的高为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1∶4的三视图中,其主视图的面积是 ( )
A.7.5 cm2 B. cm2
C.30 cm2 D. cm2
7.如图,一个透明的玻璃正方体表面嵌有一根黑色的铁丝,这根铁丝在正方体俯视图中的形状是 ( )
A B C D
8.一个立体图形由四个相同的小正方体组成,其主视图与左视图如图所示,那么原立体图形可能是①②③④中的 ( )
A.①或③ B.①或④ C.②或③ D.②或④
二、填空题(每空3分,共15分)
9.夜晚路灯下同样高的旗杆,离路灯越近,它的影子越 .(填“长”或“短”)
10.如图,这是某几何体的三视图,则这个几何体的侧面积是 .
11.如图,一个正方体由 27 个大小相同的小正方体搭成,它的三视图是3×3的正方形,现从中取走若干个小正方体,得到一个新的几何体.若新几何体的三视图仍为3×3的正方形,则最多可以取走 个正方体.
12.如图,小明从路灯下A处,向前走了5米到达D处.
(1)行走过程中,他的影子将会 (填序号).
①越来越长;②越来越短;③长度不变.
(2)在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是 米.
三、解答题(共61分)
13.(10分)如图,这是由几个小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图、左视图.
14.(12分)某食品包装盒抽象出的几何体的三视图如图所示.(俯视图为等边三角形)
(1)写出这个几何体的名称.
(2)若矩形的长为10 cm,等边三角形的边长为4 cm,求这个几何体的表面积.
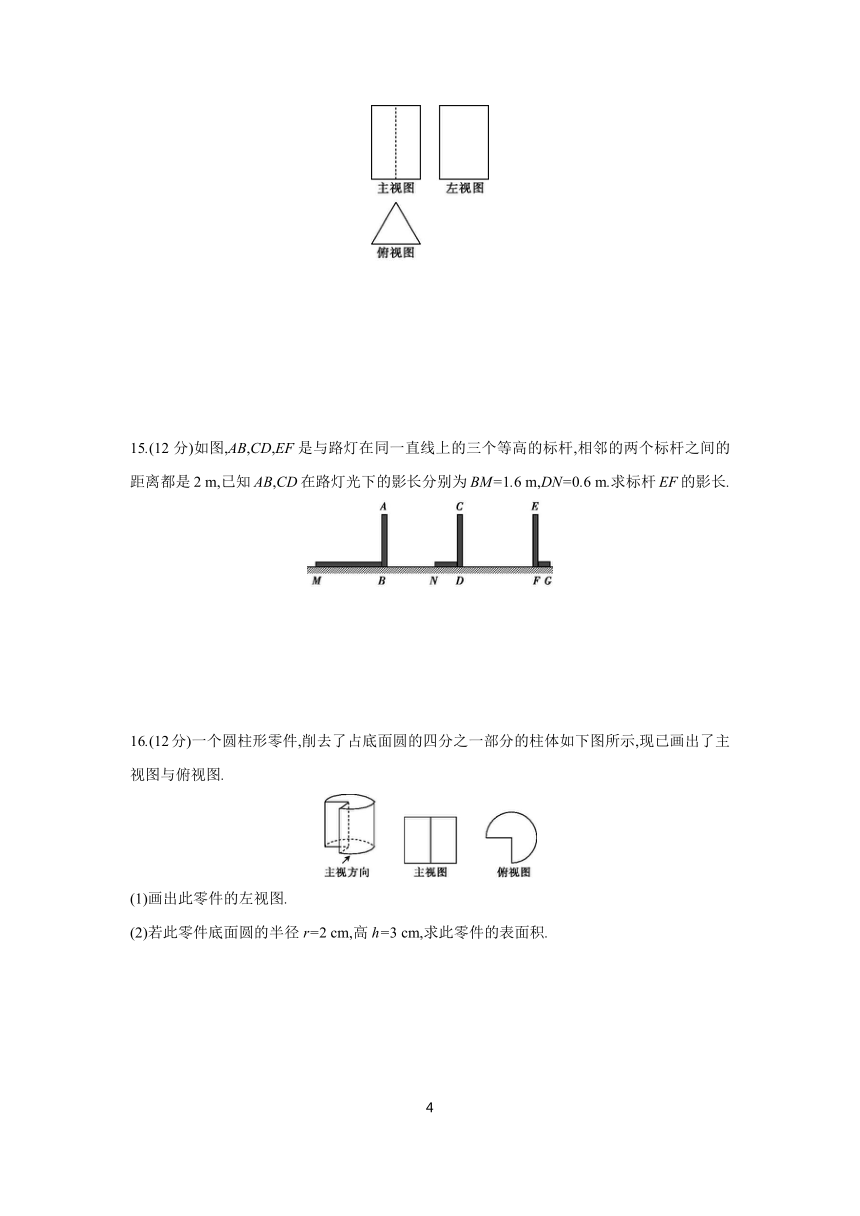
15.(12分)如图,AB,CD,EF是与路灯在同一直线上的三个等高的标杆,相邻的两个标杆之间的距离都是2 m,已知AB,CD在路灯光下的影长分别为BM=1.6 m,DN=0.6 m.求标杆EF的影长.
16.(12分)一个圆柱形零件,削去了占底面圆的四分之一部分的柱体如下图所示,现已画出了主视图与俯视图.
(1)画出此零件的左视图.
(2)若此零件底面圆的半径r=2 cm,高h=3 cm,求此零件的表面积.
17.(15分)如图,正方形ABCD的边长为4,M,N,P分别为AD,BC,CD的中点,现从点P观察线段AB,当长度为1的线段I(图中的黑粗线)以每秒1个单位长度的速度沿线MN从左向右运动时,I将阻拦部分观察视线,在△PAB区域内形成盲区,设I的右端位于M点的时刻为0,用t(秒)表示I的运动时间.
(1)请你针对图1、2、3中I位于不同位置的情形分别画在△PAB内相应的盲区,并在盲区内涂上阴影.
(2)设△PAB内的盲区面积是y(平方单位),在下列条件下,求出用t表示y的函数关系式.
①1≤t≤2;②2≤t≤3;③3≤t≤4.
根据①~③中得到的结论,请你简单概括y随t变化而变化的情况.
参考答案
1.B 2.C 3.D 4.D 5.C 6.A 7.A 8.B
9.短
10.π
11.12
12.(1)① (2)5.95
13.【解析】如图所示.
14.【解析】(1)这个几何体是三棱柱.
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长,
即C=4×3=12 cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为S=12×10=120 cm2.
这个几何体的表面积=120+2××4×2 =120+8 (cm2).
答:这个几何体的表面积为(120+8 )cm2.
15.【解析】如图,OH为路灯的高,设AB=CD=EF=a.
∵AB∥OH,
∴△MAB∽△MOH,
∴=,即=.①
∵CD∥OH,
∴△NCD∽△NOH,
∴=,即=.②
由①和②得=,
解得DH=1.2,
∴===,
HF=DF-DH=2-1.2=0.8.
∵EF∥OH,
∴△GEF∽△GOH,
∴=,即==,
解得FG=0.4.
即标杆EF的影长为0.4 m.
16.【解析】(1)如图.
(2)两底面扇形的面积=2×=6π(cm2),
竖直的两个矩形的面积=2×2×3=12(cm2),
竖直的侧面面积=×3=9π(cm2),
所以表面积=12+15π(cm2).
17.【解析】(1)如图:
(2)①当1≤t≤2时,△PAB内的盲区是梯形AEFG(如图1).
FG是△PAE的中位线,FG=t-1,AE=2(t-1),而梯形AEFG的高为2,
∴y=[(t-1)+2(t-1)]×2=3t-3.
②当2≤t≤3时,△PAB内的盲区是梯形QRST(如图2).
易知TS=1,QR=2,而梯形QRST的高为2,
∴y=×(1+2)×2=3.
③当3≤t≤4时,△PAB内的盲区是梯形WBUV(如图3).
易知UV=1-(t-3)=4-t,WB=2(4-t),而梯形的高为2,
∴y=[(4-t)+2(4-t)]×2=12-3t.
即当1≤t≤2时,盲区的面积由0逐渐增大到3;
当2≤t≤3时,盲区的面积y为定值3;
当3≤t≤4时,盲区的面积由3逐渐减小到0.
2
(建议用时:80分钟 分值:100分)
一、选择题(每小题3分,共24分)
1.下图所示的几何体的左视图是 ( )
A B C D
2.在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等,那么这两根竿子的相对位置是 ( )
A.两竿都垂直于地面
B.两竿平行斜插在地上
C.两根竿子不平行
D.一根竿倒在地上
3.若某物体的三视图如图所示,则该物体的形状可能是 ( )
A.长方体 B.圆锥体 C.正方体 D.圆柱体
4.某正方体的每个面上都有一个汉字,下图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A.厉
B.害
C.了
D.我
5.一个几何体由若干大小相同的小正方体木块搭成,它的主视图和俯视图如图所示,那么搭成该几何体所需小正方体木块的个数最少为 ( )
A.6 B.5 C.4 D.3
6.如图,空心卷筒纸的高为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1∶4的三视图中,其主视图的面积是 ( )
A.7.5 cm2 B. cm2
C.30 cm2 D. cm2
7.如图,一个透明的玻璃正方体表面嵌有一根黑色的铁丝,这根铁丝在正方体俯视图中的形状是 ( )
A B C D
8.一个立体图形由四个相同的小正方体组成,其主视图与左视图如图所示,那么原立体图形可能是①②③④中的 ( )
A.①或③ B.①或④ C.②或③ D.②或④
二、填空题(每空3分,共15分)
9.夜晚路灯下同样高的旗杆,离路灯越近,它的影子越 .(填“长”或“短”)
10.如图,这是某几何体的三视图,则这个几何体的侧面积是 .
11.如图,一个正方体由 27 个大小相同的小正方体搭成,它的三视图是3×3的正方形,现从中取走若干个小正方体,得到一个新的几何体.若新几何体的三视图仍为3×3的正方形,则最多可以取走 个正方体.
12.如图,小明从路灯下A处,向前走了5米到达D处.
(1)行走过程中,他的影子将会 (填序号).
①越来越长;②越来越短;③长度不变.
(2)在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是 米.
三、解答题(共61分)
13.(10分)如图,这是由几个小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图、左视图.
14.(12分)某食品包装盒抽象出的几何体的三视图如图所示.(俯视图为等边三角形)
(1)写出这个几何体的名称.
(2)若矩形的长为10 cm,等边三角形的边长为4 cm,求这个几何体的表面积.
15.(12分)如图,AB,CD,EF是与路灯在同一直线上的三个等高的标杆,相邻的两个标杆之间的距离都是2 m,已知AB,CD在路灯光下的影长分别为BM=1.6 m,DN=0.6 m.求标杆EF的影长.
16.(12分)一个圆柱形零件,削去了占底面圆的四分之一部分的柱体如下图所示,现已画出了主视图与俯视图.
(1)画出此零件的左视图.
(2)若此零件底面圆的半径r=2 cm,高h=3 cm,求此零件的表面积.
17.(15分)如图,正方形ABCD的边长为4,M,N,P分别为AD,BC,CD的中点,现从点P观察线段AB,当长度为1的线段I(图中的黑粗线)以每秒1个单位长度的速度沿线MN从左向右运动时,I将阻拦部分观察视线,在△PAB区域内形成盲区,设I的右端位于M点的时刻为0,用t(秒)表示I的运动时间.
(1)请你针对图1、2、3中I位于不同位置的情形分别画在△PAB内相应的盲区,并在盲区内涂上阴影.
(2)设△PAB内的盲区面积是y(平方单位),在下列条件下,求出用t表示y的函数关系式.
①1≤t≤2;②2≤t≤3;③3≤t≤4.
根据①~③中得到的结论,请你简单概括y随t变化而变化的情况.
参考答案
1.B 2.C 3.D 4.D 5.C 6.A 7.A 8.B
9.短
10.π
11.12
12.(1)① (2)5.95
13.【解析】如图所示.
14.【解析】(1)这个几何体是三棱柱.
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长,
即C=4×3=12 cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为S=12×10=120 cm2.
这个几何体的表面积=120+2××4×2 =120+8 (cm2).
答:这个几何体的表面积为(120+8 )cm2.
15.【解析】如图,OH为路灯的高,设AB=CD=EF=a.
∵AB∥OH,
∴△MAB∽△MOH,
∴=,即=.①
∵CD∥OH,
∴△NCD∽△NOH,
∴=,即=.②
由①和②得=,
解得DH=1.2,
∴===,
HF=DF-DH=2-1.2=0.8.
∵EF∥OH,
∴△GEF∽△GOH,
∴=,即==,
解得FG=0.4.
即标杆EF的影长为0.4 m.
16.【解析】(1)如图.
(2)两底面扇形的面积=2×=6π(cm2),
竖直的两个矩形的面积=2×2×3=12(cm2),
竖直的侧面面积=×3=9π(cm2),
所以表面积=12+15π(cm2).
17.【解析】(1)如图:
(2)①当1≤t≤2时,△PAB内的盲区是梯形AEFG(如图1).
FG是△PAE的中位线,FG=t-1,AE=2(t-1),而梯形AEFG的高为2,
∴y=[(t-1)+2(t-1)]×2=3t-3.
②当2≤t≤3时,△PAB内的盲区是梯形QRST(如图2).
易知TS=1,QR=2,而梯形QRST的高为2,
∴y=×(1+2)×2=3.
③当3≤t≤4时,△PAB内的盲区是梯形WBUV(如图3).
易知UV=1-(t-3)=4-t,WB=2(4-t),而梯形的高为2,
∴y=[(4-t)+2(4-t)]×2=12-3t.
即当1≤t≤2时,盲区的面积由0逐渐增大到3;
当2≤t≤3时,盲区的面积y为定值3;
当3≤t≤4时,盲区的面积由3逐渐减小到0.
2
