最新人教版七下数学 6.1 平方根 第2课时 用计算器求一个正数的的算术平方根 课件(共37张PPT)
文档属性
| 名称 | 最新人教版七下数学 6.1 平方根 第2课时 用计算器求一个正数的的算术平方根 课件(共37张PPT) | 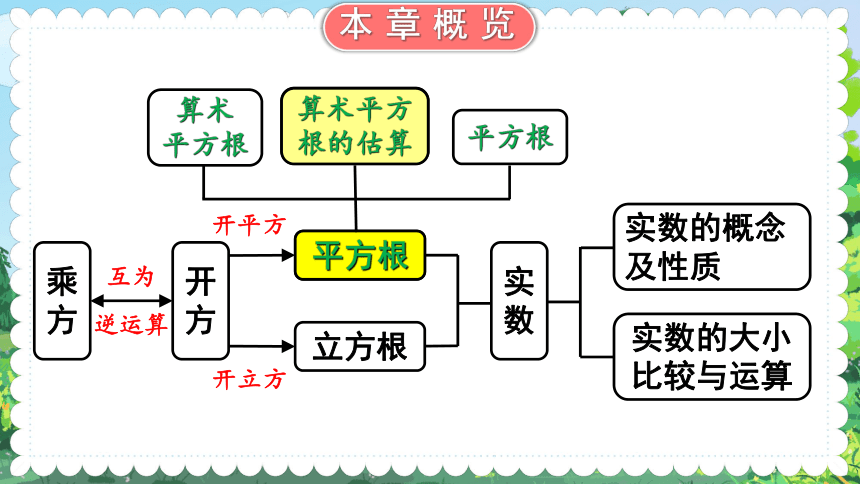 | |
| 格式 | pptx | ||
| 文件大小 | 11.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 20:18:48 | ||
图片预览







文档简介
(共37张PPT)
本章概览
乘方
开方
平方根
立方根
实数
实数的概念及性质
实数的大小比较与运算
互为
逆运算
开平方
开立方
平方根
算术 平方根
算术平方根的估算
平方根
算术平方根的估算
人教版七年级下册
第2课时 算术平方根的估算
第六章 实数
6.1 平方根
抢答——判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
14
7
0.7
196 -4 0.49 (-7)2 0
0
复习回顾
探究新知
探究一
能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
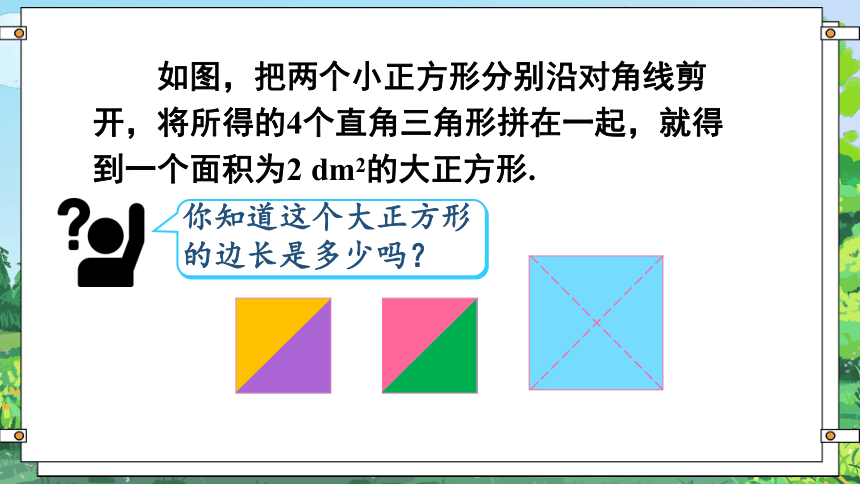
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
你知道这个大正方形的边长是多少吗?
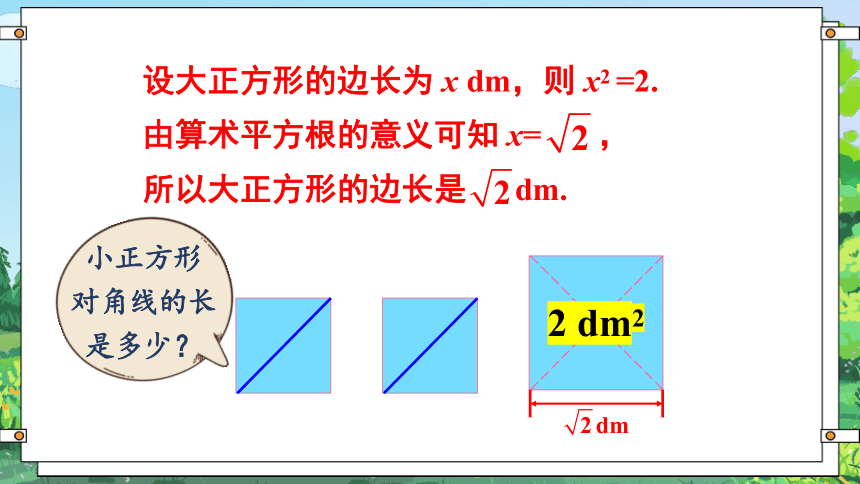
设大正方形的边长为 x dm,则 x2 =2.
由算术平方根的意义可知 x= ,
所以大正方形的边长是 dm.
2 dm2
小正方形 对角线的长是多少?
有多大呢?
探究新知
探究二
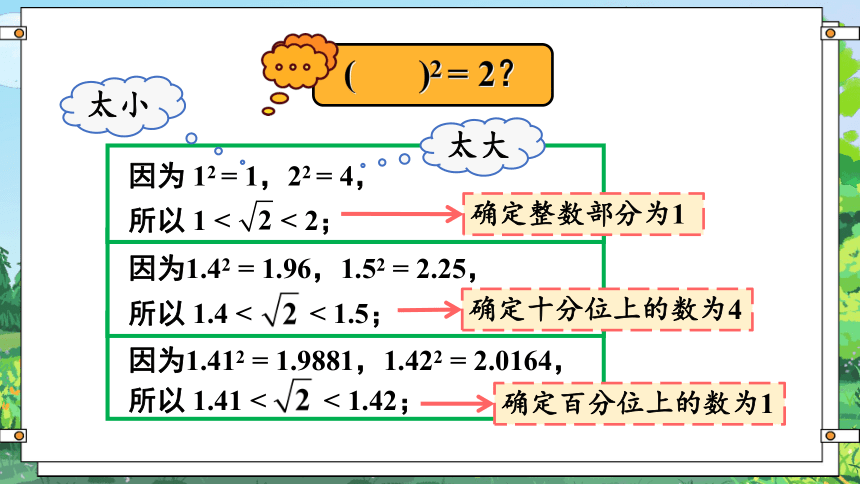
因为1.412 = 1.9881,1.422 = 2.0164,
所以 1.41 < < 1.42;
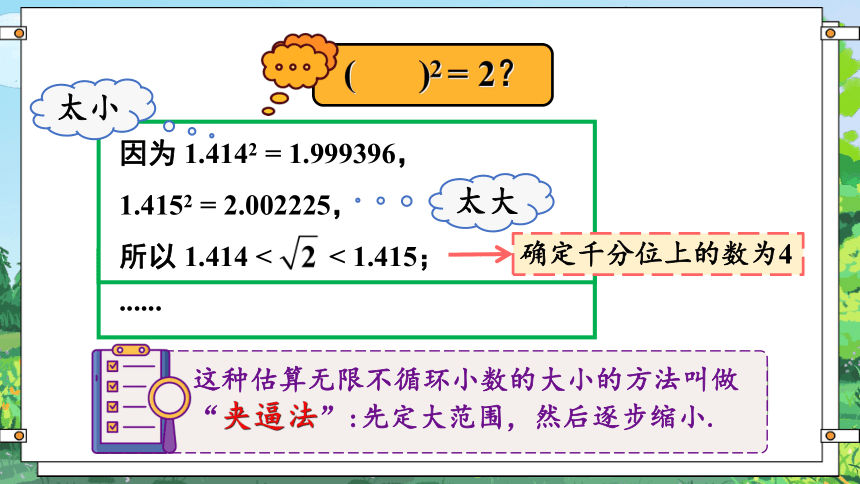
( )2 = 2?
因为1.42 = 1.96,1.52 = 2.25,
所以 1.4 < < 1.5;
太小
太大
因为 12 = 1,22 = 4,
所以 1 < < 2;
确定整数部分为1
确定十分位上的数为4
确定百分位上的数为1
太小
太大
因为 1.4142 = 1.999396,
1.4152 = 2.002225,
所以 1.414 < < 1.415;
......
( )2 = 2?
如此进行下去,可以得到 的更精确的近似值.
确定千分位上的数为4
这种估算无限不循环小数的大小的方法叫做“夹逼法”:先定大范围,然后逐步缩小.
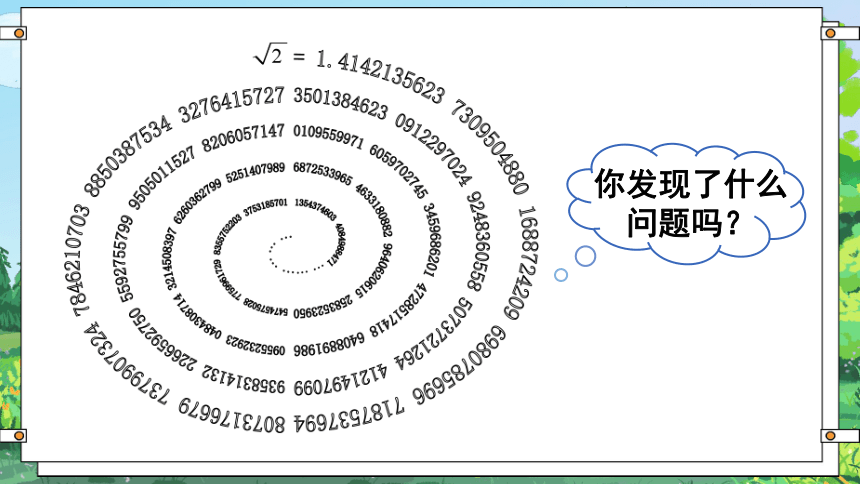
你发现了什么问题吗?
概念
提取
事实上, =1.414 213 562 373...,它是一个无限不循环小数.
无限不循环小数
无限不循环小数是指小数位数无限,且小数部分不循环的小数,你以前见过这种数吗?
实际上,如 等,许多正有理数的算术平方根都是无限不循环小数.
π也是无限不循环小数.
1. 填写下列表格:
方法(对两个连续整数或小数用平方法逐步进行比较) 步骤
通过估算,确定 在哪两个连续的整数之间
通过估算,确定 在哪两个连续的一位小数之间
因为22=4,32=9,
所以2< <3
因为2.62=6.76,2.72=7.29,
所以2.6< <2.7
对应训练
方法(对两个连续整数或小数用平方法逐步进行比较) 步骤
通过估算,确定 在哪两个连续的两位小数之间
通过估算,确定 在哪两个连续的三位小数之间
······ ······
因为2.6452=6.996025,
2.6462=7.001316,
所以2.645< <2.646
因为2.642=6.9696,
2.652=7.0225,
所以2.64< <2.65
2. 估计 的值在( )
A. 2和3之间 B. 3和4之间
C. 4和5之间 D. 5和6之间
B
解析:因为32=9,42=16,所以3< <4.
大多数计算器都有 键,用它可以求出一个正有理数的算术平方根(或其近似值).
例 2 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(1)依次按键 3 1 3 6 ,
=
显示:56.
不同品牌的计算器,按键顺序有所不同.
准确数
例 2 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(2)依次按键 2 ,
=
显示:1.414213562.
计算器上显示的1.414 213 562是 的近似值.
近似数
现在你能计算第一宇宙速度和第二宇宙速度了吗?
已知:
用计算器求v1,v2的值(用科学计数法把结果写成a×10n的形式,其中a保留小数点后一位).
v12 =gR
,v22 =2gR
,g ≈ 9.8 m/s2
,R ≈ 6.4×106 m.
对应训练
已知:v12 =gR,v22 =2gR,g ≈ 9.8 m/s2,R ≈ 6.4×106 m.
用计算器求v1,v2的值(用科学计数法把结果写成a×10n的形式,其中a保留小数点后一位).
解:由 v12 =gR,v22 =2gR,得
用计算器求 v1和 v2,得
因此,第一宇宙速度v1大约是7.9×103m/s,第二宇宙速度v2大约是1.1×104m/s.
探究三
利用计算器探究被开方数的小数点与算术平方根的小数点的移动规律
(1)利用计算器计算下表中的算术平方根,并将计算结果填在表中.
... ...
... ...
0.25
0.791
2.5
7.91
25
79.1
250
你发现了什么?
... ...
... ...
0.25
0.791
2.5
7.91
25
79.1
250
规律:被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
2
2
1
1
你能说出其中的道理吗?
(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出 的近似值,你能根据 的值说出 是多少吗?
根据(1)中发现的规律,得
解:用计算器计算 ,得 .
根据 的值不能说出 是多少.
小数点只移动了一位,不符合规律.
1. 用计算器计算下列各式的值.
(1) ;(2) ;(3) (精确到0.01).
37
2.24
10.06
【选自教材P44练习 第1题】
对应训练
2.(1) 已知 ______,116.42≈ _____;
(2)若 ,则
_____;
(3)已知 则
_____(精确到0.01).
11.64
13540
1.01
-4.50
现实中,除了使用计算器计算算术平方根的值(或其近似值),还经常需要估计一个数的大小.
例 3 小丽想用一块面积为400 cm2的正方形纸片,沿着边的方向裁出一块面积为300 cm2 的长方形纸片,使它的长宽之比为3:2. 她不知能否裁得出来,正在发愁. 小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
400 cm2
300 cm2
求长方形纸片的长
解:设长方形纸片的长为 3x cm,宽为 2x cm.
根据边长与面积的关系得
3x · 2x = 300,
6x2 = 300,
x2 = 50,
因此长方形纸片的长为 cm.
就是 .
300 cm2
cm
因为 50____49,所以 ____7 .
由上可知 3 > _____ .
即长方形纸片的长应该大于 21 cm.
比较数的大小
>
>
21
大于21 cm
300 cm2
cm
答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片 .
根据结果做出判断
因为 =20,所以正方形纸片的边长只有 20 cm .
300 cm2
大于21 cm
cm
400 cm2
20 cm
这样,长方形纸片的长将大于正方形纸片的边长 .
比较下列各组数的大小:
(1) 与 ; (2) 与 8;
(3) 与 0.5;(4) 与 1.
【选自教材P44练习 第2题】
比较含有算术平方根的两个数的大小:
①被开方数越大,对应的算术平方根也越大;
②估算的近似值越大,原数也越大.
对应训练
(1) 与 ;
解:因为 8<10,
所以 .
(2) 与 8;
解:因为 82=64,
所以 .
因为 65>64,所以 ,
即 .
(3) 与 0.5;
(4) 与 1.
解:因为 5 > 4,
所以 ,
所以 ,
所以 .
解:因为 5 < 9,
所以 ,
所以 ,
所以 .
1. 用计算器计算下列各式的值(精确到0.01):
【选自教材P47习题6.1 第5题】
(1) ;
(2) ;
(3) ;
(4) ;
随堂练习
【选自教材P47习题6.1 第6题】
2. 估计与 最接近的两个整数是多少.
解:由 36 < 40 < 49,得 6 < < 7.
故与 最接近的两个整数是6,7 .
3. 任意找一个正数,比如 1234,利用计算器对它开平方,再对得到的算术平方根开平方......如此进行下去,你有什么发现?
【选自教材P48习题6.1 第12题】
答:对于 1:
对于小于 1 的正数:
对于大于 1 的正数:
每次开平方所得的算术平方根均为 1;
每次开平方所得的算术平方根逐渐增大,并趋近于 1;
每次开平方所得的算术平方根逐渐减小,并趋近于 1.
用“夹逼法”估计算术平方根的大小
用计算器求算术平方根
利用估算比较大小
无限不循环小数
. . . . . . .
课堂小结
课后作业
完成对应课时的练习.
本章概览
乘方
开方
平方根
立方根
实数
实数的概念及性质
实数的大小比较与运算
互为
逆运算
开平方
开立方
平方根
算术 平方根
算术平方根的估算
平方根
算术平方根的估算
人教版七年级下册
第2课时 算术平方根的估算
第六章 实数
6.1 平方根
抢答——判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
14
7
0.7
196 -4 0.49 (-7)2 0
0
复习回顾
探究新知
探究一
能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
你知道这个大正方形的边长是多少吗?
设大正方形的边长为 x dm,则 x2 =2.
由算术平方根的意义可知 x= ,
所以大正方形的边长是 dm.
2 dm2
小正方形 对角线的长是多少?
有多大呢?
探究新知
探究二
因为1.412 = 1.9881,1.422 = 2.0164,
所以 1.41 < < 1.42;
( )2 = 2?
因为1.42 = 1.96,1.52 = 2.25,
所以 1.4 < < 1.5;
太小
太大
因为 12 = 1,22 = 4,
所以 1 < < 2;
确定整数部分为1
确定十分位上的数为4
确定百分位上的数为1
太小
太大
因为 1.4142 = 1.999396,
1.4152 = 2.002225,
所以 1.414 < < 1.415;
......
( )2 = 2?
如此进行下去,可以得到 的更精确的近似值.
确定千分位上的数为4
这种估算无限不循环小数的大小的方法叫做“夹逼法”:先定大范围,然后逐步缩小.
你发现了什么问题吗?
概念
提取
事实上, =1.414 213 562 373...,它是一个无限不循环小数.
无限不循环小数
无限不循环小数是指小数位数无限,且小数部分不循环的小数,你以前见过这种数吗?
实际上,如 等,许多正有理数的算术平方根都是无限不循环小数.
π也是无限不循环小数.
1. 填写下列表格:
方法(对两个连续整数或小数用平方法逐步进行比较) 步骤
通过估算,确定 在哪两个连续的整数之间
通过估算,确定 在哪两个连续的一位小数之间
因为22=4,32=9,
所以2< <3
因为2.62=6.76,2.72=7.29,
所以2.6< <2.7
对应训练
方法(对两个连续整数或小数用平方法逐步进行比较) 步骤
通过估算,确定 在哪两个连续的两位小数之间
通过估算,确定 在哪两个连续的三位小数之间
······ ······
因为2.6452=6.996025,
2.6462=7.001316,
所以2.645< <2.646
因为2.642=6.9696,
2.652=7.0225,
所以2.64< <2.65
2. 估计 的值在( )
A. 2和3之间 B. 3和4之间
C. 4和5之间 D. 5和6之间
B
解析:因为32=9,42=16,所以3< <4.
大多数计算器都有 键,用它可以求出一个正有理数的算术平方根(或其近似值).
例 2 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(1)依次按键 3 1 3 6 ,
=
显示:56.
不同品牌的计算器,按键顺序有所不同.
准确数
例 2 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(2)依次按键 2 ,
=
显示:1.414213562.
计算器上显示的1.414 213 562是 的近似值.
近似数
现在你能计算第一宇宙速度和第二宇宙速度了吗?
已知:
用计算器求v1,v2的值(用科学计数法把结果写成a×10n的形式,其中a保留小数点后一位).
v12 =gR
,v22 =2gR
,g ≈ 9.8 m/s2
,R ≈ 6.4×106 m.
对应训练
已知:v12 =gR,v22 =2gR,g ≈ 9.8 m/s2,R ≈ 6.4×106 m.
用计算器求v1,v2的值(用科学计数法把结果写成a×10n的形式,其中a保留小数点后一位).
解:由 v12 =gR,v22 =2gR,得
用计算器求 v1和 v2,得
因此,第一宇宙速度v1大约是7.9×103m/s,第二宇宙速度v2大约是1.1×104m/s.
探究三
利用计算器探究被开方数的小数点与算术平方根的小数点的移动规律
(1)利用计算器计算下表中的算术平方根,并将计算结果填在表中.
... ...
... ...
0.25
0.791
2.5
7.91
25
79.1
250
你发现了什么?
... ...
... ...
0.25
0.791
2.5
7.91
25
79.1
250
规律:被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
2
2
1
1
你能说出其中的道理吗?
(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出 的近似值,你能根据 的值说出 是多少吗?
根据(1)中发现的规律,得
解:用计算器计算 ,得 .
根据 的值不能说出 是多少.
小数点只移动了一位,不符合规律.
1. 用计算器计算下列各式的值.
(1) ;(2) ;(3) (精确到0.01).
37
2.24
10.06
【选自教材P44练习 第1题】
对应训练
2.(1) 已知 ______,116.42≈ _____;
(2)若 ,则
_____;
(3)已知 则
_____(精确到0.01).
11.64
13540
1.01
-4.50
现实中,除了使用计算器计算算术平方根的值(或其近似值),还经常需要估计一个数的大小.
例 3 小丽想用一块面积为400 cm2的正方形纸片,沿着边的方向裁出一块面积为300 cm2 的长方形纸片,使它的长宽之比为3:2. 她不知能否裁得出来,正在发愁. 小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
400 cm2
300 cm2
求长方形纸片的长
解:设长方形纸片的长为 3x cm,宽为 2x cm.
根据边长与面积的关系得
3x · 2x = 300,
6x2 = 300,
x2 = 50,
因此长方形纸片的长为 cm.
就是 .
300 cm2
cm
因为 50____49,所以 ____7 .
由上可知 3 > _____ .
即长方形纸片的长应该大于 21 cm.
比较数的大小
>
>
21
大于21 cm
300 cm2
cm
答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片 .
根据结果做出判断
因为 =20,所以正方形纸片的边长只有 20 cm .
300 cm2
大于21 cm
cm
400 cm2
20 cm
这样,长方形纸片的长将大于正方形纸片的边长 .
比较下列各组数的大小:
(1) 与 ; (2) 与 8;
(3) 与 0.5;(4) 与 1.
【选自教材P44练习 第2题】
比较含有算术平方根的两个数的大小:
①被开方数越大,对应的算术平方根也越大;
②估算的近似值越大,原数也越大.
对应训练
(1) 与 ;
解:因为 8<10,
所以 .
(2) 与 8;
解:因为 82=64,
所以 .
因为 65>64,所以 ,
即 .
(3) 与 0.5;
(4) 与 1.
解:因为 5 > 4,
所以 ,
所以 ,
所以 .
解:因为 5 < 9,
所以 ,
所以 ,
所以 .
1. 用计算器计算下列各式的值(精确到0.01):
【选自教材P47习题6.1 第5题】
(1) ;
(2) ;
(3) ;
(4) ;
随堂练习
【选自教材P47习题6.1 第6题】
2. 估计与 最接近的两个整数是多少.
解:由 36 < 40 < 49,得 6 < < 7.
故与 最接近的两个整数是6,7 .
3. 任意找一个正数,比如 1234,利用计算器对它开平方,再对得到的算术平方根开平方......如此进行下去,你有什么发现?
【选自教材P48习题6.1 第12题】
答:对于 1:
对于小于 1 的正数:
对于大于 1 的正数:
每次开平方所得的算术平方根均为 1;
每次开平方所得的算术平方根逐渐增大,并趋近于 1;
每次开平方所得的算术平方根逐渐减小,并趋近于 1.
用“夹逼法”估计算术平方根的大小
用计算器求算术平方根
利用估算比较大小
无限不循环小数
. . . . . . .
课堂小结
课后作业
完成对应课时的练习.
