平行四边形的性质（二）

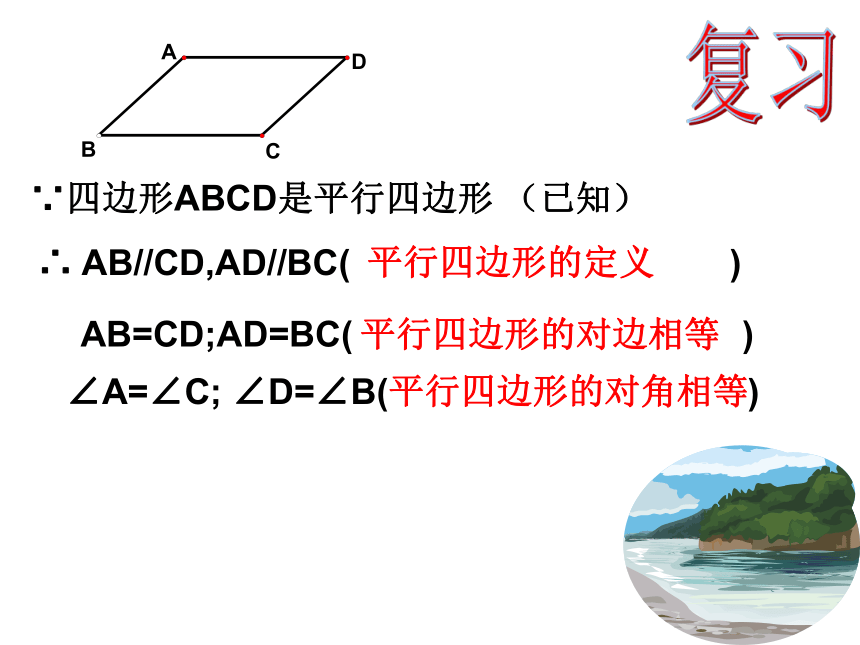
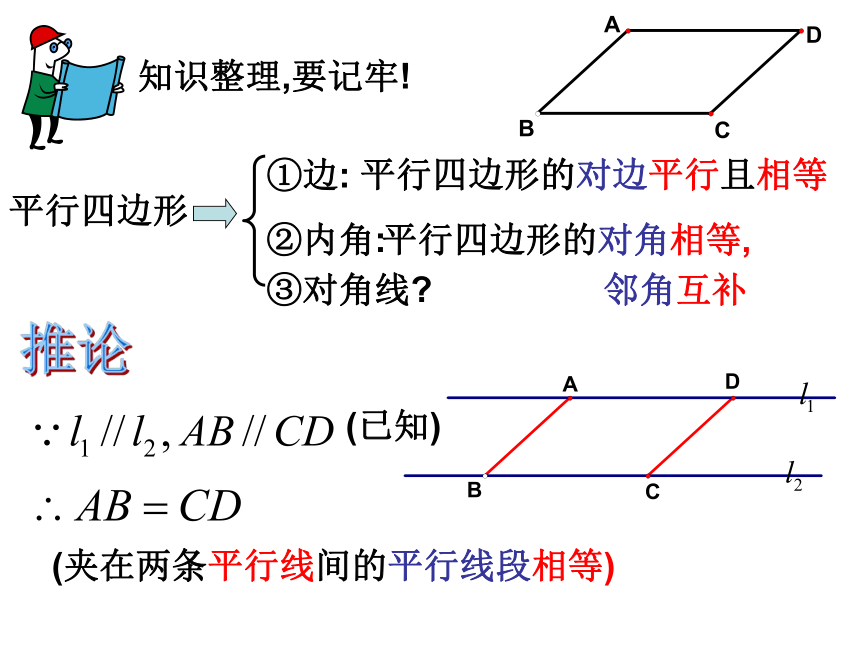
课件17张PPT。22.2平行四边形2AB=CD;AD=BC( )平行四边形的对边相等复习∵四边形ABCD是平行四边形 （已知）∠A=∠C; ∠D=∠B( )平行四边形的对角相等∴ AB//CD,AD//BC( )平行四边形的定义(夹在两条平行线间的平行线段相等)推论(已知)知识整理,要记牢!平行四边形①边:平行四边形的对边平行且相等②内角:平行四边形的对角相等,
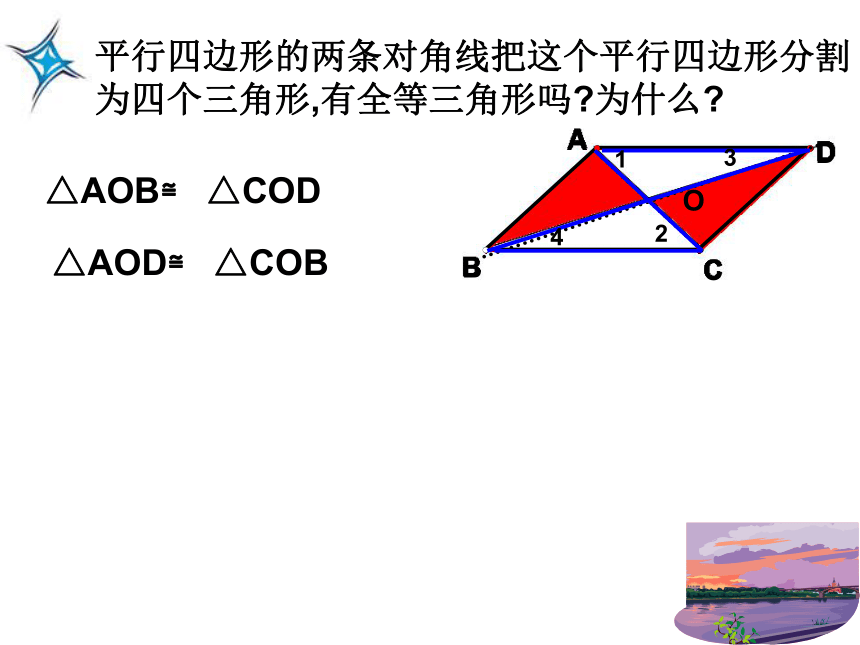
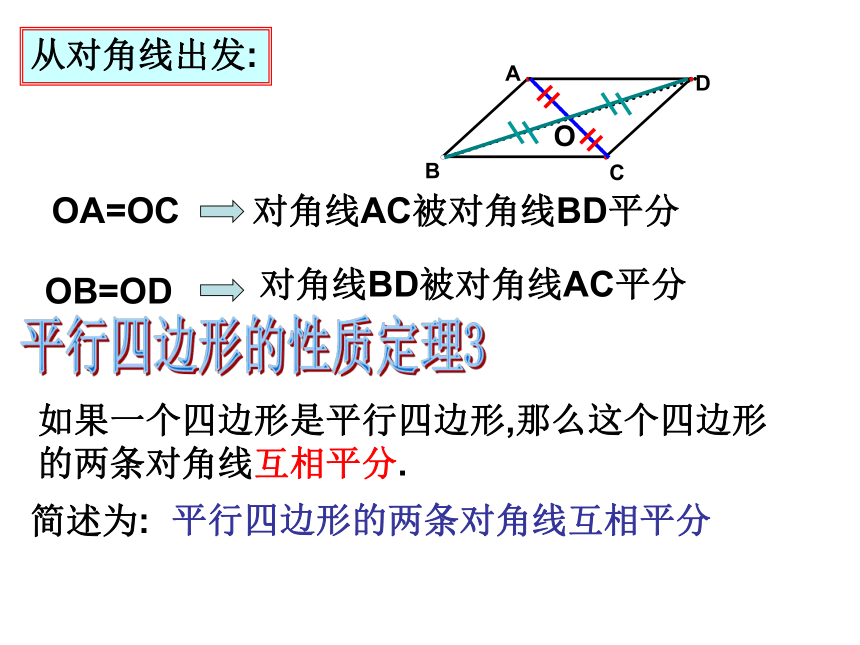
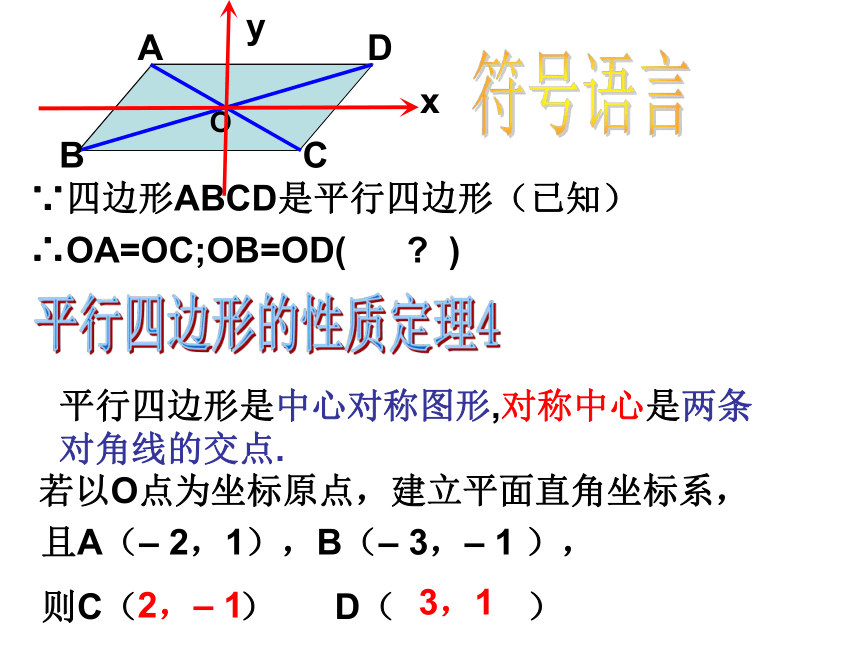
邻角互补③对角线?平行四边形的两条对角线把这个平行四边形分割为四个三角形,有全等三角形吗?为什么?O△AOB≌ △COD△AOD≌ △COB1234从对角线出发:OOA=OC对角线AC被对角线BD平分OB=OD对角线BD被对角线AC平分平行四边形的性质定理3如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分.简述为:平行四边形的两条对角线互相平分OBACD平行四边形的性质定理4∵四边形ABCD是平行四边形（已知）符号语言∴OA=OC;OB=OD( ? )平行四边形是中心对称图形,对称中心是两条对角线的交点.xy且A（– 2，1），B（– 3，– 1 ），
则C（ ） D（ ）2，– 13，1若以O点为坐标原点，建立平面直角坐标系，平行四边形①边:平行四边形的对边平行且相等②内角:平行四边形的对角相等,
③对角线：知识整理,要记牢!平行四边形的两条对角线
互相平分④对称性：平行四边形是中心对称图形1. 已知O是□ABCD两条对角线的交点,AC=24cm,BC=38cm,OD=28cm,则△OBC的周长为__________.78cm解：∵四边形ABCD是平行四边形（平行四边形对角线互相平分）又∵ AC=24cm，OD=28cm（已知）∴△OBC的周长= OB+OC+BC=28+12+38=78cm ∵ BC=38cm（已知）∴OC= =12cm ，OB=OD=28cm例题讲解：2.如图2, ABCD的对角线AC,BD相交于点O,已知AB=5cm, △OAB周长比△BOC的周长短3cm,则AD的长是_____.∵C△OAB= BO+AO+AB ,
C△BOC= CO+BO+BC（已知）∴AD＝BC（平行四边形的对边相等） 解： ∵四边形ABCD是平行四边形（已知）∴ AD = BC = 8cm 8cm ∵ AB = 5cm（已知）又∵C△OAB+ 3=C△BOC（已知）∴ AB+3=BC（平行四边形的对角线互相平分）OA＝OC例题讲解：例题讲解：3.有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm，它的一边长为18cm?为什么?若设平行四边形的一边长为xcm，则x的取值范围为多少？∴ 3cm＜AD＜17cm∵四边形ABCD是平行四边形（平行四边形对角线互相平分）∵AC=20cm,BD=14cm（已知）∴OA=OC=10cm，OB=OD=7cm∴OA=OC= ， OB=OD=∴在△OAD中，|OA-OD|∴不存在这样的平行四边形。例题4、平行四边形ABCD中 ,对角线AC、BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F，求证:OE=OFF顺便问：上图中有几对全等三角形？EO证明：∵四边形ABCD是平行四边形∵ AD∥BC（平行四边形的定义）∴∠1 = ∠2（两直线平行，内错角相等）又∵ ∠3= ∠4（对顶角相等）∴OA=OC（平行四边形对角线互相平分）∴△AOE≌△COF∴OE = OF新课：5、一块如图所示的钢板，如何用一条直线将其分为面积相等的两部分.练习1、已知，在平行四边形ABCD中，E、F
分别是BC、AD上的点，且AE//CF，
求证∠BAE=∠DCF完成书后练习证明：∵AD∥BC又∵ AE∥CF∴四边形AECF为平行四边形∴ ∠EAF= ∠FCE（平行四边形对角相等）∴∠BAD –∠ EAF = ∠DCB – ∠FCE 即∠BAE = ∠DCF同理 ∠BAD= ∠DCB练习2一边长为5米的平行四边形，它的对角线长可能是（ ）A 4米和6米B 4米和3米C 2米和6米D 4米和8米D3、在平面直角坐标系中，平行四边形ABCD
的边//x轴，B、D均在y轴上，且A、D在
直线y = 2x – 1上，且B（0，1），
求平行四边形ABCD的面积小结2．平行四边形的图形特征？1 本节课重点学习了平行四边形的性质定理是什么？3 你还有哪些收获？回家作业1、中午完成练习册22.2（2）2、一课一练22.2（2）3、预习书P75-77/22.2（3）
并完成书后练习