平行四边形的判定
图片预览




文档简介
课件17张PPT。平行四边形的判定 (1)复习:
1、平行四边形定义是什么?两组对边分别平行的四边形
叫做平行四边形 互相平分平行四边形边角对角线对角相等,邻角互补对称性中心对称图形2、请你简述平行四边形的性质对边平行且相等 平行四边形边?角?对角线?方向:
怎样判定一个四边形是平行四边形?思考:
怎样判定一个四边形是平行四边形?定义:
两组对边分别平行的四边形叫做
平行四边形。定义永远可以作为判定定理。思考:∵AB∥CD且AD∥BC(已知),
∴四边形ABCD是平行四边形.(平行四边形的定义)符号语言: 通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线相互平分。那么这些命题的逆命题成立吗??思考:有两组对边分别相等的四边形是平行四边形;已知:四边形ABCD中,AB=CD,AD=CB. 求证:四边形ABCD是 平行四边形 从边出发:判定定理1:证明:联结AC∴△ABC≌△CDA∵ AB=CD,AD=CB,AC=CA∴∠CAB=∠ACD,∠ACB= ∠ CAD∴AB∥CD,AD∥BC∴四边形ABCD是平行四边形
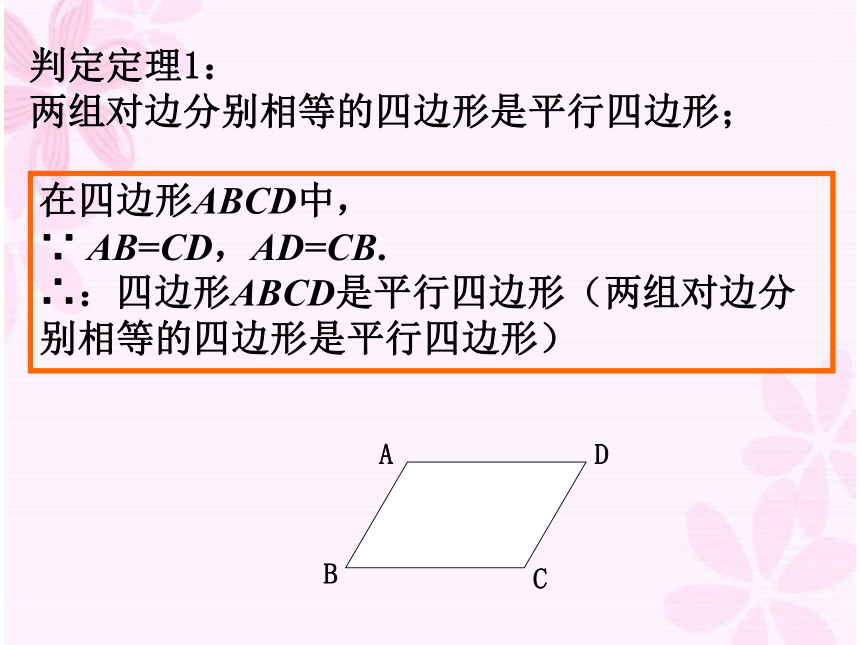
(平行四边形的定义)判定定理1:
两组对边分别相等的四边形是平行四边形;在四边形ABCD中, ∵ AB=CD,AD=CB. ∴:四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)ADBC判定定理2:已知:四边形ABCD中, AB∥CD,AB = CD. 求 证:四边形ABCD是 平行四边形一组对边平行且相等的四边形是平行四边形证明:联结AC∴△ABC≌△CDA∵ AB∥CD∴∠CAB=∠ACD,∠ACB= ∠ CAD∴AB∥CD,AD∥BC∴四边形ABCD是平行四边形 (平行四边形的定义)12∴∠1 = ∠2又∵AB=CD,AC = CA在四边形ABCD中, ∵ AB∥CD,AB = CD. ∴ 四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)判定定理2:
一组对边平行且相等的四边形是平行四边形ADBC一组对边平行,一组对边相等的四边形是平行四边形吗?小结深化到目前判定平行四边形的方法:两组对边分别平行(定义)两组对边分别相等(判定1)一组对边平行且相等(判定2)可判定四边形
是平行四边形从边出发:完成课后练习P77例1、在□ABCD中,E、F分别为CD、AB的中点
求证:四边形EFGH是平行四边形。证明:∵ 四边形ABCD为平行四边形∴四边形DEBF为平行四边形( )∴DF∥EB∴四边形EFGH是平行四边形 (平行四边形的定义)又∵E、F是AB、CD的中点同理 AE∥FC例2、△ABD、△ACF、△BCE都是等边三角形
求证四边形ADEF为平行四边形。证明:∵ △ABD,△BCE是等边三角形∴△DBE≌△ABC∴DE = AC∴四边形ADEF是平行四边形 ( )∴AB=BD,BC=BE
∠ABD = 60°=∠CBE∴∠ABC =∠DBE∵ △ACF是等边三角形∴AF = AC∴AF = DE同理 AD = FE
已知:平行四边形ABCD中,AE⊥BD于E,
CF⊥BD于F.
求证:四边形AECF是平行四边形例3 证△ABE≌ △ CDF(一组对边平行且相等的四边形是平行四边形)得AE=CF由AE⊥BD,CF⊥BD得:
AE ∥ CF
从而证得四边形AECF是平行四边形思路点拨:你还有其它方法吗?
已知:如图,在平行四边形ABCD中,∠1=∠2,
求证:EF和AC互相平分 证明:∵ 四边形ABCD是平行四边形∴△DAE≌△BCF∴AE = CF,DE = BF∴四边形AECF是平行四边形 ( )∴CD = AB,AD = BC,
∠D = ∠B又∵∠1 =∠2即EC = FA∴EF和AC互相平分∴CD – DE = AB – BF又∵AE = CF 课堂小结:回家作业:1、校内完成练习册22.2(3)节作业。2、一课一练22.2(3)3、预习书P77—79,完成P79练习
1、平行四边形定义是什么?两组对边分别平行的四边形
叫做平行四边形 互相平分平行四边形边角对角线对角相等,邻角互补对称性中心对称图形2、请你简述平行四边形的性质对边平行且相等 平行四边形边?角?对角线?方向:
怎样判定一个四边形是平行四边形?思考:
怎样判定一个四边形是平行四边形?定义:
两组对边分别平行的四边形叫做
平行四边形。定义永远可以作为判定定理。思考:∵AB∥CD且AD∥BC(已知),
∴四边形ABCD是平行四边形.(平行四边形的定义)符号语言: 通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线相互平分。那么这些命题的逆命题成立吗??思考:有两组对边分别相等的四边形是平行四边形;已知:四边形ABCD中,AB=CD,AD=CB. 求证:四边形ABCD是 平行四边形 从边出发:判定定理1:证明:联结AC∴△ABC≌△CDA∵ AB=CD,AD=CB,AC=CA∴∠CAB=∠ACD,∠ACB= ∠ CAD∴AB∥CD,AD∥BC∴四边形ABCD是平行四边形
(平行四边形的定义)判定定理1:
两组对边分别相等的四边形是平行四边形;在四边形ABCD中, ∵ AB=CD,AD=CB. ∴:四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)ADBC判定定理2:已知:四边形ABCD中, AB∥CD,AB = CD. 求 证:四边形ABCD是 平行四边形一组对边平行且相等的四边形是平行四边形证明:联结AC∴△ABC≌△CDA∵ AB∥CD∴∠CAB=∠ACD,∠ACB= ∠ CAD∴AB∥CD,AD∥BC∴四边形ABCD是平行四边形 (平行四边形的定义)12∴∠1 = ∠2又∵AB=CD,AC = CA在四边形ABCD中, ∵ AB∥CD,AB = CD. ∴ 四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)判定定理2:
一组对边平行且相等的四边形是平行四边形ADBC一组对边平行,一组对边相等的四边形是平行四边形吗?小结深化到目前判定平行四边形的方法:两组对边分别平行(定义)两组对边分别相等(判定1)一组对边平行且相等(判定2)可判定四边形
是平行四边形从边出发:完成课后练习P77例1、在□ABCD中,E、F分别为CD、AB的中点
求证:四边形EFGH是平行四边形。证明:∵ 四边形ABCD为平行四边形∴四边形DEBF为平行四边形( )∴DF∥EB∴四边形EFGH是平行四边形 (平行四边形的定义)又∵E、F是AB、CD的中点同理 AE∥FC例2、△ABD、△ACF、△BCE都是等边三角形
求证四边形ADEF为平行四边形。证明:∵ △ABD,△BCE是等边三角形∴△DBE≌△ABC∴DE = AC∴四边形ADEF是平行四边形 ( )∴AB=BD,BC=BE
∠ABD = 60°=∠CBE∴∠ABC =∠DBE∵ △ACF是等边三角形∴AF = AC∴AF = DE同理 AD = FE
已知:平行四边形ABCD中,AE⊥BD于E,
CF⊥BD于F.
求证:四边形AECF是平行四边形例3 证△ABE≌ △ CDF(一组对边平行且相等的四边形是平行四边形)得AE=CF由AE⊥BD,CF⊥BD得:
AE ∥ CF
从而证得四边形AECF是平行四边形思路点拨:你还有其它方法吗?
已知:如图,在平行四边形ABCD中,∠1=∠2,
求证:EF和AC互相平分 证明:∵ 四边形ABCD是平行四边形∴△DAE≌△BCF∴AE = CF,DE = BF∴四边形AECF是平行四边形 ( )∴CD = AB,AD = BC,
∠D = ∠B又∵∠1 =∠2即EC = FA∴EF和AC互相平分∴CD – DE = AB – BF又∵AE = CF 课堂小结:回家作业:1、校内完成练习册22.2(3)节作业。2、一课一练22.2(3)3、预习书P77—79,完成P79练习
