平行四边形判定(二)
图片预览





文档简介
课件20张PPT。平行四边形
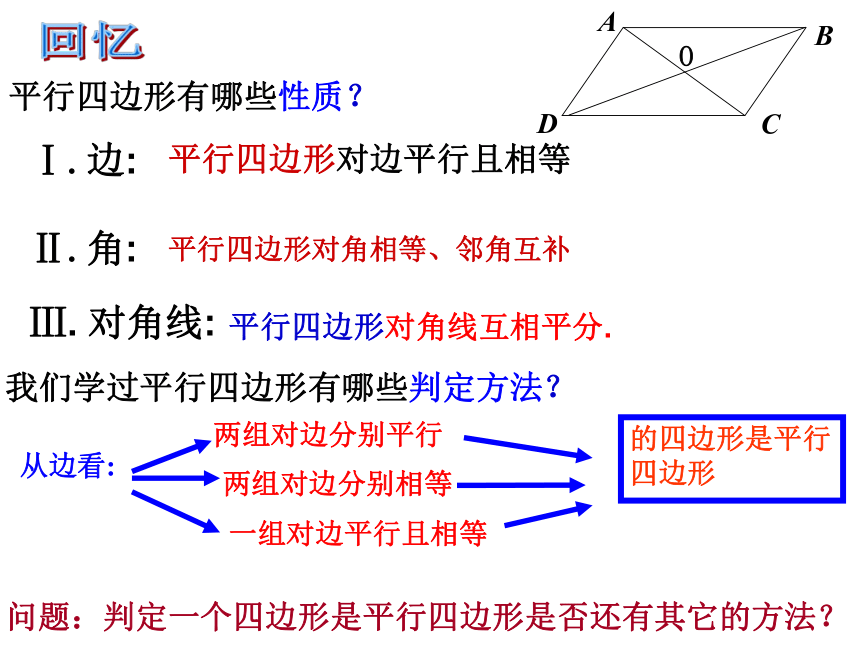
的判定(2)回忆平行四边形有哪些性质? 平行四边形对角线互相平分.我们学过平行四边形有哪些判定方法? 从边看: 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 问题:判定一个四边形是平行四边形是否还有其它的方法?平行四边形对边平行且相等平行四边形对角相等、邻角互补 从角出发?
从对角线出发??思考:对角线互相平分的四边形是平行四边形
两组对角分别相等的四边形是平行四边形已知:如图,四边形ABCD的对角线AC,BD相交于点O,并且AO=CO,BO=DO,求证:四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形证明: 在△ AOB和△COD中,
∵OA=OC,∠AOB= ∠ COD, OB=OD
∴ △ AOB ≌ △COD
∴ AB=CD, ∠BAO= ∠DCO
∴AB∥CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)已知:四边形ABCD的对角线AC、BD交于点O,
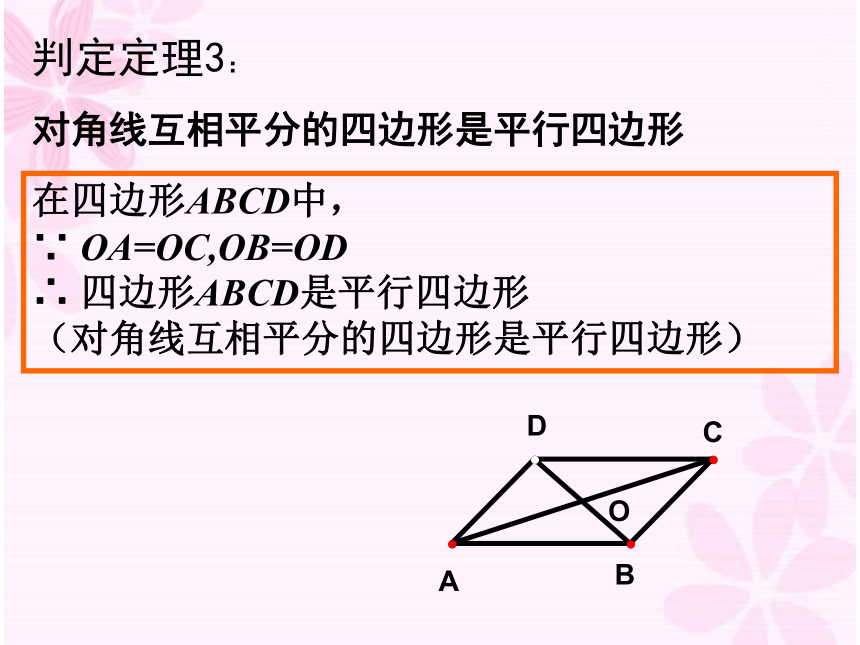
OA=OC,OB=OD求证:四边形ABCD是平行四边形.在四边形ABCD中, ∵ OA=OC,OB=OD ∴ 四边形ABCD是平行四边形 (对角线互相平分的四边形是平行四边形)判定定理3:
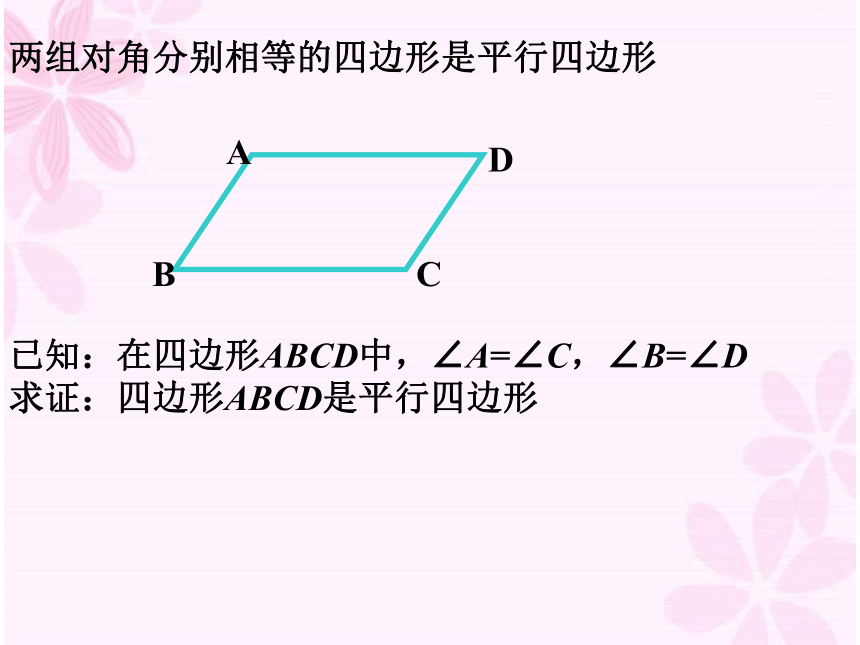
对角线互相平分的四边形是平行四边形已知:在四边形ABCD中,∠A=∠C,∠B=∠D 求证:四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形 已知:如图,四边形ABCD,∠A= ∠C, ∠B= ∠D
求证:四边形ABCD是平行四边形.
证明:∵∠A= ∠C, ∠B= ∠D 又∵∠A+∠B+∠C+∠D=360°
(四边形内角和为360度)∴ 2∠A+2∠B =360°∴ ∠A+∠B =180°∴ AD∥BC同理得:AB∥CD∴四边形ABCD是平行四边形
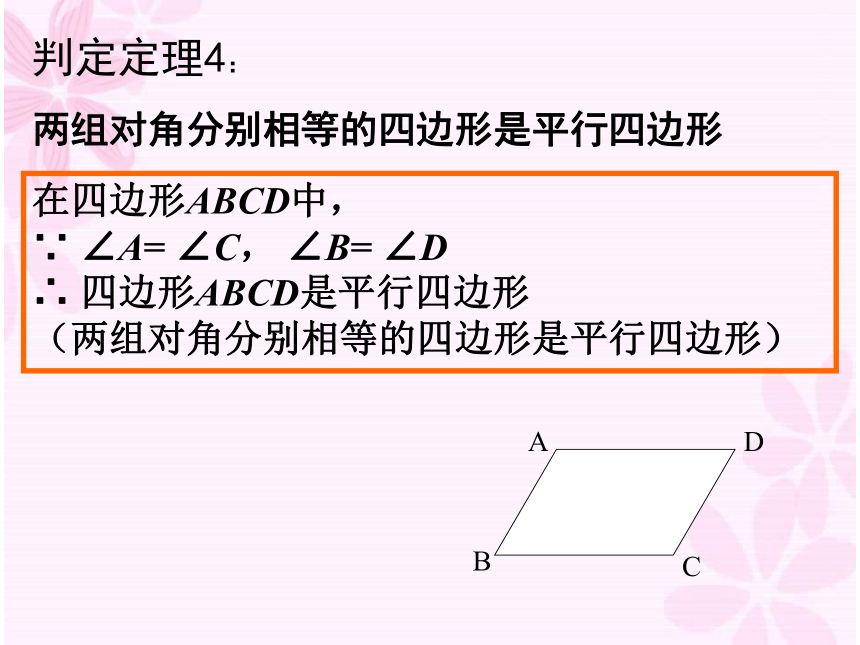
(平行四边形的定义)在四边形ABCD中, ∵ ∠A= ∠C, ∠B= ∠D ∴ 四边形ABCD是平行四边形 (两组对角分别相等的四边形是平行四边形)判定定理4:
两组对角分别相等的四边形是平行四边形ADBC证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵ AE=CF,
∴ AO – AE =CO – CF
即 EO=FO.
又∵ BO=DO,
∴四边形BFDE是平行四边形.已知:平行四边形ABCD中,AE、CF分别是
∠ BAD 、 ∠ BCD 的平分线,分别交
BC和AD于E、F.
求证:四边形AECF是平行四边形30例2证明:∵四边形ABCD是平行四边形,
∴ ∠DAB = ∠BCD ,∠B = ∠D
∵∠1 = ∠2 = 0.5∠DAB,
∠3 = ∠4 = 0.5∠ BCD
∴ ∠1 = ∠2 = ∠3 = ∠4
∴ ∠1 + ∠B = ∠4 + ∠D.
即 ∠ AEC = ∠CFA,
∵∠2 = ∠3
∴四边形AECF是平行四边形.1234判定定理3: 对角线互相平分的四边形是平行四边形判定定理4: 两组对角分别相等的四边形是平行四边形判定定理1
两组对边分别相等的四边形是平行四边形判定定理2: 一组对边平行且相等的四边形是平行四边形定义:
两组对边分别平行的四边形是平行四边形平行四边形的判定方法从边出发定义从角出发从对角线出发请你识别下列四边形哪些是平行四边形?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝已知:平行四边形ABCD的对角线AC,BD相交于点O,M,N分别是OA,OC的中点 求证:BM//DN且BM=DN例3 证明:联结DM,BN在□ABCD中,OA = OC,OB = OD( )∴OM = ON∵OB = OD∴四边形BMDN是平行四边形( )∴BM//DN且BM=DN ( )例4、已知:如图四边形ABCD是平行四边形,
延长DA到E使AE = BE,延长BC到F使CF = DF
求证:四边形BEDF是平行四边形
证明:在□ABCD中,AB = CD,AD = BC
∠ABC = ∠ADC, ∠DAB =∠ BCD,∴∠EAB = ∠DCF∵AE= BE,CF = DF∴∠EAB = ∠EBA,∠DCF = ∠CDF∴ ∠EBA = ∠CDF,∴△EBA≌△FDC∵∠EAB + ∠DAB=180°,∠DCF + ∠BCD=180°∵∠EAB = ∠DCF,AB = CD∴BE = DF AE = CF∵AD = BC∴ED = FB∵BE = FD
∴四边形BEDF是
平行四边形DABCFEO 已知:O为平行四边形ABCD的对角线
AC的中点,EF经过点O,且与AB交于
E,与CD交于F。
求证:四边形AECF是平行四边形。练习证明:∵AB ∥ CD,∴∠ACD = ∠CAB∵AO= CO,∴△COF≌△AOE∴ OF = OE又∵∠COF = ∠AOE∵AO= CO,∴四边形AECF是
平行四边形
已知:平行四边形ABCD相交于点O,M,N,P,Q分别是OA,OB,OC,OD的中点。求证:四边形MNPQ是平行四边形。DABCQMNPO练习 完成课后习题证明:在□ABCD中,
OA=OC,OB=OD∴OM = OP同理OQ = ON∴MNPQ是平行四边形已知:如图求证:四边形MNOP是
平行四边形.数学联想:1、题目中给我们了一些什么条件?2、由MO⊥ON联想到什么?边长(含x)、MO⊥ON勾股定理、求x平行四边形的判别方法:AB∥CDAD∥BCAB∥CDAB=CDOB=OD平行四边形ABCD平行四边形ABCD平行四边形ABCD∠A=∠C∠B=∠D平行四边形ABCDOA=OC回家作业:1、校内完成练习册22.2(4)节作业。2、一课一练22.2(4)3、预习书P79—81,完成P81练习
的判定(2)回忆平行四边形有哪些性质? 平行四边形对角线互相平分.我们学过平行四边形有哪些判定方法? 从边看: 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 问题:判定一个四边形是平行四边形是否还有其它的方法?平行四边形对边平行且相等平行四边形对角相等、邻角互补 从角出发?
从对角线出发??思考:对角线互相平分的四边形是平行四边形
两组对角分别相等的四边形是平行四边形已知:如图,四边形ABCD的对角线AC,BD相交于点O,并且AO=CO,BO=DO,求证:四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形证明: 在△ AOB和△COD中,
∵OA=OC,∠AOB= ∠ COD, OB=OD
∴ △ AOB ≌ △COD
∴ AB=CD, ∠BAO= ∠DCO
∴AB∥CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)已知:四边形ABCD的对角线AC、BD交于点O,
OA=OC,OB=OD求证:四边形ABCD是平行四边形.在四边形ABCD中, ∵ OA=OC,OB=OD ∴ 四边形ABCD是平行四边形 (对角线互相平分的四边形是平行四边形)判定定理3:
对角线互相平分的四边形是平行四边形已知:在四边形ABCD中,∠A=∠C,∠B=∠D 求证:四边形ABCD是平行四边形两组对角分别相等的四边形是平行四边形 已知:如图,四边形ABCD,∠A= ∠C, ∠B= ∠D
求证:四边形ABCD是平行四边形.
证明:∵∠A= ∠C, ∠B= ∠D 又∵∠A+∠B+∠C+∠D=360°
(四边形内角和为360度)∴ 2∠A+2∠B =360°∴ ∠A+∠B =180°∴ AD∥BC同理得:AB∥CD∴四边形ABCD是平行四边形
(平行四边形的定义)在四边形ABCD中, ∵ ∠A= ∠C, ∠B= ∠D ∴ 四边形ABCD是平行四边形 (两组对角分别相等的四边形是平行四边形)判定定理4:
两组对角分别相等的四边形是平行四边形ADBC证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵ AE=CF,
∴ AO – AE =CO – CF
即 EO=FO.
又∵ BO=DO,
∴四边形BFDE是平行四边形.已知:平行四边形ABCD中,AE、CF分别是
∠ BAD 、 ∠ BCD 的平分线,分别交
BC和AD于E、F.
求证:四边形AECF是平行四边形30例2证明:∵四边形ABCD是平行四边形,
∴ ∠DAB = ∠BCD ,∠B = ∠D
∵∠1 = ∠2 = 0.5∠DAB,
∠3 = ∠4 = 0.5∠ BCD
∴ ∠1 = ∠2 = ∠3 = ∠4
∴ ∠1 + ∠B = ∠4 + ∠D.
即 ∠ AEC = ∠CFA,
∵∠2 = ∠3
∴四边形AECF是平行四边形.1234判定定理3: 对角线互相平分的四边形是平行四边形判定定理4: 两组对角分别相等的四边形是平行四边形判定定理1
两组对边分别相等的四边形是平行四边形判定定理2: 一组对边平行且相等的四边形是平行四边形定义:
两组对边分别平行的四边形是平行四边形平行四边形的判定方法从边出发定义从角出发从对角线出发请你识别下列四边形哪些是平行四边形?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝已知:平行四边形ABCD的对角线AC,BD相交于点O,M,N分别是OA,OC的中点 求证:BM//DN且BM=DN例3 证明:联结DM,BN在□ABCD中,OA = OC,OB = OD( )∴OM = ON∵OB = OD∴四边形BMDN是平行四边形( )∴BM//DN且BM=DN ( )例4、已知:如图四边形ABCD是平行四边形,
延长DA到E使AE = BE,延长BC到F使CF = DF
求证:四边形BEDF是平行四边形
证明:在□ABCD中,AB = CD,AD = BC
∠ABC = ∠ADC, ∠DAB =∠ BCD,∴∠EAB = ∠DCF∵AE= BE,CF = DF∴∠EAB = ∠EBA,∠DCF = ∠CDF∴ ∠EBA = ∠CDF,∴△EBA≌△FDC∵∠EAB + ∠DAB=180°,∠DCF + ∠BCD=180°∵∠EAB = ∠DCF,AB = CD∴BE = DF AE = CF∵AD = BC∴ED = FB∵BE = FD
∴四边形BEDF是
平行四边形DABCFEO 已知:O为平行四边形ABCD的对角线
AC的中点,EF经过点O,且与AB交于
E,与CD交于F。
求证:四边形AECF是平行四边形。练习证明:∵AB ∥ CD,∴∠ACD = ∠CAB∵AO= CO,∴△COF≌△AOE∴ OF = OE又∵∠COF = ∠AOE∵AO= CO,∴四边形AECF是
平行四边形
已知:平行四边形ABCD相交于点O,M,N,P,Q分别是OA,OB,OC,OD的中点。求证:四边形MNPQ是平行四边形。DABCQMNPO练习 完成课后习题证明:在□ABCD中,
OA=OC,OB=OD∴OM = OP同理OQ = ON∴MNPQ是平行四边形已知:如图求证:四边形MNOP是
平行四边形.数学联想:1、题目中给我们了一些什么条件?2、由MO⊥ON联想到什么?边长(含x)、MO⊥ON勾股定理、求x平行四边形的判别方法:AB∥CDAD∥BCAB∥CDAB=CDOB=OD平行四边形ABCD平行四边形ABCD平行四边形ABCD∠A=∠C∠B=∠D平行四边形ABCDOA=OC回家作业:1、校内完成练习册22.2(4)节作业。2、一课一练22.2(4)3、预习书P79—81,完成P81练习
