平行四边形判定及性质的应用
图片预览



文档简介
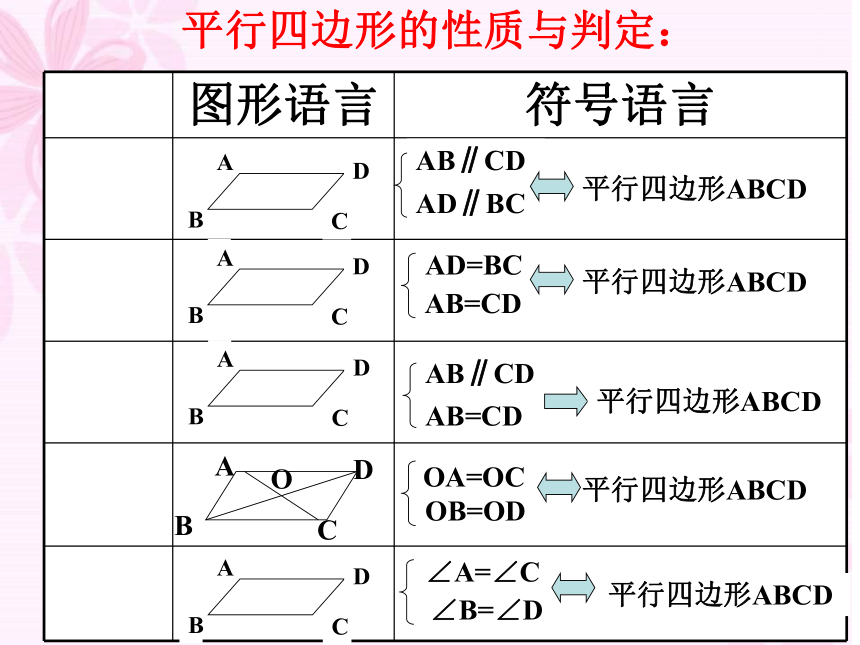
课件11张PPT。平行四边形的性质与判定平行四边形的性质与判定:AB∥CDAD∥BCAB∥CDAB=CDOB=OD平行四边形ABCDAB=CDAD=BC平行四边形ABCD平行四边形ABCD平行四边形ABCD∠A=∠C∠B=∠D平行四边形ABCDOA=OC已知四边形ABCD,从(1)AB∥CD;(2)AB = CD;
(3)AD∥BC;(4)AD = BC;(5)∠A = ∠C;
(6)∠B = ∠D中取两个条件加以组合,能推出
ABCD是平行四边形的有哪几种情形?共9种情形:(a)(1)(3)(b)(1)(2)(c)(3)(4)(d)(2)(4)(e)(5)(6)(f)(1)(5)(g)(1)(6)(h)(3)(5)(i)(3)(6)已知:平行四边形ABCD中,点E、F 、 G、H分别
在边AD 、 AB、 BC 、CD上,且 DE= BG ,
AF=CH.
求证 (1)EF=GH
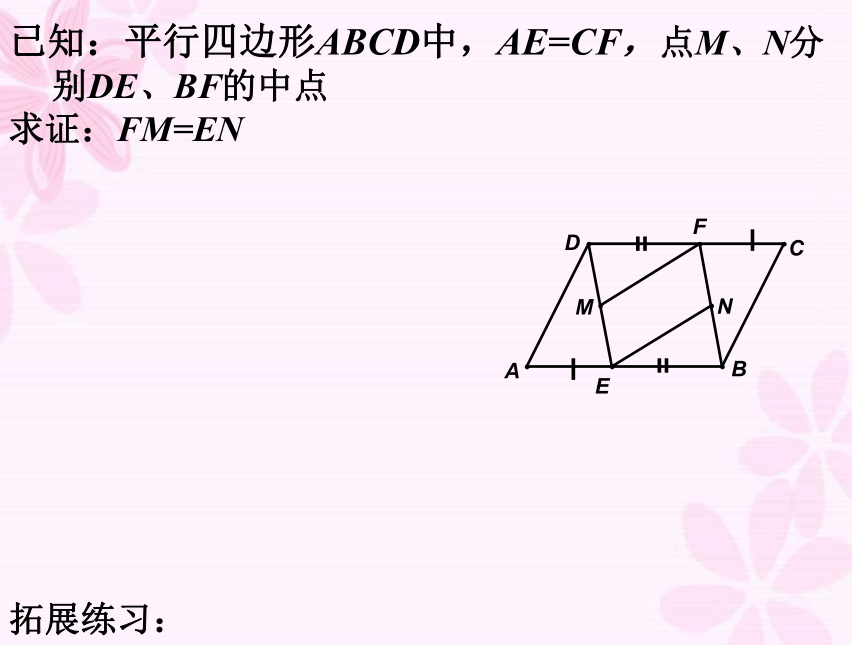
(2)EG和HF互相平分例1完成课后练习P81已知:平行四边形ABCD中,AE=CF,点M、N分别DE、BF的中点
求证:FM=EN拓展练习:已知:平行四边形ABCD中,对角线AC、BD相交
于点O,AE⊥BD于E,BF⊥AC于F,CG⊥BD于点G,
DH⊥AC于H
求证:四边形EFGH是平行四边形拓展练习:证△AOE≌ △COG(对角线互相平分的四边形是平行四边形)得OE=OG同理可得 OF = OH
从而证得四边形EFGH是平行四边形思路点拨:已知:AD是Rt△ABC斜边BC上的高,∠B的平分线
交AD于点E,过点E作EF∥BC交AC于点F
求证:AE = FC拓展练习:证四边形CFEG是平行四边形从而得EG = AE
可得 EG = FC再证△ABE≌△GBE(A.A.S)思路点拨:因此有 AE = FC
过E作EG∥AC已知:在四边形ABCD中,DC∥AB,以AC、AD为
边作□ACED,延长DC交EB于点F
求证:EF = FB拓展练习:证四边形ABGD是平行四边形从而得四边形CEGB是平行四边形
可得 BG 与 AD平行且相等由AD与CE平行且相等可得BG与CE平行且相等思路点拨:因此有 EF = FB
过B作BG平行AD对于下列猜想,正确的给出证明,错误的举出反例1、一组对边平行,一组对角相等的四边形是平行四边形;2、一组对边平行,另一组对边相等的四边形是平行四边形;3、一组对边相等,一组对角相等的四边形是平行四边形;4、一组对边相等,一条对角线平分另一条对角线的
四边形是平行四边形;5、一组对边平行,一条对角线平分另一条对角线的
四边形是平行四边形;6、一组对角相等,一条对角线平分另一条对角线的
四边形是平行四边形;×√√×××小结:在解有关平行四边形的问题时,要灵活运用平行
四边形的性质定理及判定定理,要仔细观察图形,
分析已知条件,从而找到合适的方法解题回家作业:1、校内完成练习册22.2(5)节作业。2、一课一练22.2(5)3、节假日作业
(3)AD∥BC;(4)AD = BC;(5)∠A = ∠C;
(6)∠B = ∠D中取两个条件加以组合,能推出
ABCD是平行四边形的有哪几种情形?共9种情形:(a)(1)(3)(b)(1)(2)(c)(3)(4)(d)(2)(4)(e)(5)(6)(f)(1)(5)(g)(1)(6)(h)(3)(5)(i)(3)(6)已知:平行四边形ABCD中,点E、F 、 G、H分别
在边AD 、 AB、 BC 、CD上,且 DE= BG ,
AF=CH.
求证 (1)EF=GH
(2)EG和HF互相平分例1完成课后练习P81已知:平行四边形ABCD中,AE=CF,点M、N分别DE、BF的中点
求证:FM=EN拓展练习:已知:平行四边形ABCD中,对角线AC、BD相交
于点O,AE⊥BD于E,BF⊥AC于F,CG⊥BD于点G,
DH⊥AC于H
求证:四边形EFGH是平行四边形拓展练习:证△AOE≌ △COG(对角线互相平分的四边形是平行四边形)得OE=OG同理可得 OF = OH
从而证得四边形EFGH是平行四边形思路点拨:已知:AD是Rt△ABC斜边BC上的高,∠B的平分线
交AD于点E,过点E作EF∥BC交AC于点F
求证:AE = FC拓展练习:证四边形CFEG是平行四边形从而得EG = AE
可得 EG = FC再证△ABE≌△GBE(A.A.S)思路点拨:因此有 AE = FC
过E作EG∥AC已知:在四边形ABCD中,DC∥AB,以AC、AD为
边作□ACED,延长DC交EB于点F
求证:EF = FB拓展练习:证四边形ABGD是平行四边形从而得四边形CEGB是平行四边形
可得 BG 与 AD平行且相等由AD与CE平行且相等可得BG与CE平行且相等思路点拨:因此有 EF = FB
过B作BG平行AD对于下列猜想,正确的给出证明,错误的举出反例1、一组对边平行,一组对角相等的四边形是平行四边形;2、一组对边平行,另一组对边相等的四边形是平行四边形;3、一组对边相等,一组对角相等的四边形是平行四边形;4、一组对边相等,一条对角线平分另一条对角线的
四边形是平行四边形;5、一组对边平行,一条对角线平分另一条对角线的
四边形是平行四边形;6、一组对角相等,一条对角线平分另一条对角线的
四边形是平行四边形;×√√×××小结:在解有关平行四边形的问题时,要灵活运用平行
四边形的性质定理及判定定理,要仔细观察图形,
分析已知条件,从而找到合适的方法解题回家作业:1、校内完成练习册22.2(5)节作业。2、一课一练22.2(5)3、节假日作业
