物理人教版(2019)必修第二册5.2运动的合成与分解(共39张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册5.2运动的合成与分解(共39张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 35.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-05 09:25:35 | ||
图片预览











文档简介
(共39张PPT)
5.2 运动的合成与分解
人教版(2019)物理(必修第二册)
第五单元 曲线运动
如何研究复杂的运动?
1.将放有红蜡块的玻璃管倒置在水平的电动滑轨上,向右匀速运动,观察红蜡块的运动轨迹。
实验探究
2 .将玻璃管中注满清水并倒放静置,观察红蜡块的运动轨迹
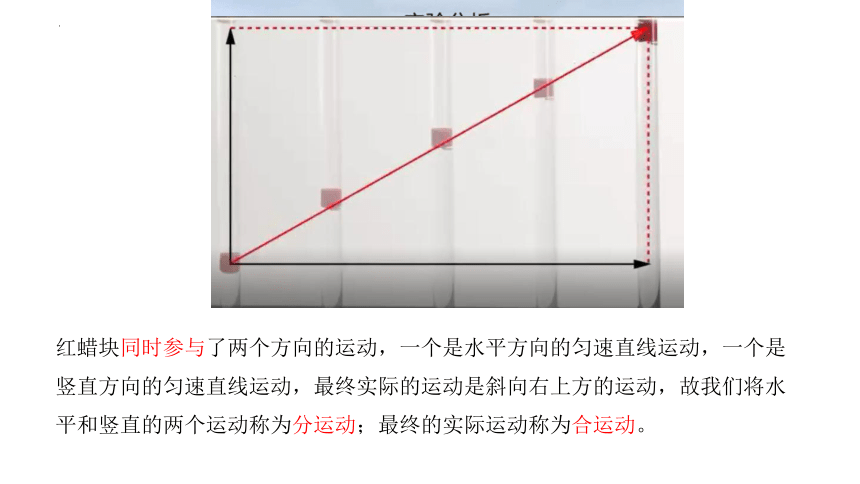
3 .将玻璃管中注满清水,并倒置在电动滑轨上,则红蜡块的运动轨迹是怎样的呢?
斜向右上方的直线运动
红蜡块同时参与了两个方向的运动,一个是水平方向的匀速直线运动,一个是竖直方向的匀速直线运动,最终实际的运动是斜向右上方的运动,故我们将水平和竖直的两个运动称为分运动;最终的实际运动称为合运动。
运动的合成与分解
01.
合运动
分运动
运动的合成
运动的分解
⑴遵循规律:平行四边形法则
⑵分解原则:通常根据运动的实际效果分解,也可以正交分解。
a
a1
a2
v1
v2
v
⑶运动的合成与分解是指 x、v、 a 的合成与分解。
A
B
x
x1
x2
位移的合成
速度的合成
加速度的合成
合运动与分运动的关系
05.
2. 独立性——各分运动独立进行,互不影响
3. 等效性——各分运动叠加起来与合运动有相同的效果
1. 等时性——分运动和合运动是同时开始和结束,时间相同。
4. 同体性——各分运动与合运动是同一个物体的运动
可以等效替代
一、合运动和分运动
定量分析:设经时间t,蜡块从O点运动到P点。
O
x
y
P
( x,y)
Vx
Vy
S
θ
x
y
水平:
竖直:
x=vxt
y=vyt
位移
大小:
方向:
轨迹
速度
大小:
方向:
结论:蜡块的运动轨
迹是条直线
例题:某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是 0.15m,自动扶梯与水平面的夹角为 30°,自动扶梯前进的速度是 0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
解:如图所示,甲在竖直方向的速度
v甲y=v甲sinθ=0.76×sin30°m/s=0.38m/s
乙在竖直方向的速度
因此v甲y >v乙,甲先到楼上。
甲比乙先到达楼上,甲上楼用了12s。
30°
v甲y
v甲
新课讲授
【典例】下列对运动的合成与分解的理解正确的是( )
A.质点的合位移一定大于两分位移
B.质点运动时,合运动的时间等于两分运动所需时间之和
C.质点的合速度等于两分速度的代数和
D.质点的合速度应为两分速度的矢量和
D
在下图所示的实验中,如果将玻璃管紧贴着黑板沿水平方向向右匀加速移动,若玻璃管内壁是光滑的,蜡块的轨迹还是一条直线吗?
蜡块的轨迹不再是一条直线,而是一条曲线。
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
互成角度的两个直线运动的合运动
不在同一直线上的两个匀速直线运动的合运动是什么运动?
匀速直线运动
v2
v1
v合
F合= 0
匀变速曲线运动。
不在同一直线上的匀速直线运动和匀变速直线运动的合运动是什么运动?
v1
F
v2
v合
思考:
1.两个匀速直线运动的合运动一定是匀速直线运动
2.一个匀速直线运动和一个匀变速直线运动的合运动一定是匀变速曲线运动
3.两个匀加速直线运动的合运动:
初速度均为零:一定是匀加速直线运动
初速度均不为零:匀变速运动(可能直线也可能曲线)
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
如图所示,在一张白纸上放置一根直尺,沿直尺的边缘放置一块直角三角板.将三角板沿直尺水平向右匀速直线运动,同时将一支铅笔从三角板直角边的最下端沿直角边向上运动,而且向上的速度越来越大,则铅笔在纸上留下的痕迹可能是( )
A. B. C. D.
C
【例题】如图所示,红蜡块能在竖直放置并装满水的玻璃管中匀速上升,若红蜡块从A点开始,沿玻璃管匀速上升的同时,使玻璃管水平向右做直线运动且玻璃管到CD处时红蜡块恰在D点,则下列说法不正确的是 ( )
A.若玻璃管匀速运动,则蜡块的轨迹为直线P
B.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线R
C.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线Q
D.若玻璃管匀减速运动,则蜡块的轨迹可能为曲线R
B
高中物理必修第二册课件
例题1
例题精选
01.
在蜡块的运动实验中,若蜡块从A点匀速上升,同时玻璃管水平向右做直线运动,蜡块最终到达C点。蜡块从A点到C点可能的4种运动轨迹如图所示,下列说法正确的
B.轨迹2中的蜡块运动时间最长
C.轨迹3也可能是玻璃管向右做匀加速直线运动形成的
D.四个轨迹中的蜡块平均速度相等
D
2.一物体在竖直平面内运动,它在竖直方向的速度时间图像和水平方向的位移时间图像分别如图甲、乙所示。关于物体运动说法正确的是( )
A.零时刻的速度为2m/s
B.加速度a=1m/s2
C.物体做匀变速直线运动
D.物体做变加速曲线运动
B
典例
小船渡河问题
1.小船参与的两个分运动
(1)船相对水的运动(即船在静水中的运动),它的方向与船头的指向相同。
(2)船随水漂流的运动,它的方向与河岸平行。
d
2.区别三个速度:水流速度v水、船在静水中的速度v船、船的实际速度(即船的合速度)v合。
1.求过河最短时间?船头冲哪个方向?
2.求过河最短位移?船头冲哪个方向?
分析小船如何渡河时间最短?
所有船速都用来过河最快。
V水
想快啊?船头朝着河岸开就对了!
最短时间:
此时位移AC:
一、小船过河(最短时间)
船头垂直于河岸
小船如何渡河才能使渡河位移最小?
位移最小等于河宽。
在非静水中开船,想办法让合运动垂直河岸方向,
船头朝向上游,船头与河岸的夹角为θ
一、小船过河(最短位移)
合运动垂直河岸方向
1.当v船>v水,
最短位移:xmin=d
渡河时间:t=
2.当v船 < v水
一、小船过河(最短位移)
船不能垂直于河岸渡河,怎样渡河位移最小?
d
v水
lmin
A
v船
θ
θ
θ
v
v船
最短位移:
渡河时间:
例、小船在宽度为100 m的河流中行驶,若它在静水中航行速度为4 m/s,水流速度为3 m/s,下列说法正确的是( )A.小船能到达出发点的正对岸B.小船在30 s时间内不可能渡过此河C.小船在河流中的航行速度大小一定为5 m/sD.若小船用最短时间渡河,则它的位移是100 m
A
5.如图所示,一条小船渡河,河宽为100m,河水流速v1=3m/s,船在静水中速度v2=4m/s,船头方向与河岸垂直,关于小船的运动,下列说法正确的是( )
A.小船的实际运动轨迹与河岸垂直
B.小船相对于河岸的速度大小为7m/s
C.小船过河后航行到了河对岸下游75m处
D.若小船行驶到河中央时,水流急速加快,则运动时间也会随之变短
4. 一船在静水中的速度为3m/s,要横渡宽为30m,流速为4m/s的河流,下列说法中不正确的是( )
A:此船能垂直到达河对岸
B:此船不可能垂直到达河对岸
C:此船相对河岸速度一定为5m/s
D:过河时间可能为15s
4. 一船在静水中的速度为3m/s,要横渡宽为30m,流速为4m/s的河流,下列说法中不正确的是( )
A:此船能垂直到达河对岸
B:此船不可能垂直到达河对岸
C:此船相对河岸速度一定为5m/s
D:过河时间可能为15s
典例
二、关联运动问题
v
θ
A
B
C
关联运动:一般是两个(或两个以上)物体通过轻绳或轻杆联系在一起。绳、杆两端所连接的物体的速度可以是不同的,但两端的物体沿绳或杆方向的速度大小一定相等
v
θ
v∥
沿绳
垂直于绳
v⊥
v船
解题技巧:
①确定合速度(实际运动)
②将实际速度分解——沿绳(杆)、垂直于绳(杆);
③作矩形——利用三角函数求解;
特点:根据两个物体沿绳(杆)方向的速度大小相等解题
1.A穿在光滑的竖直杆上,当B以速度v0匀速沿斜面体下滑时,使物体A到达如图所示位置,绳与竖直杆的夹角为θ,连接B的绳子始终与斜面体平行,则物体A上升的速度是( )
A. B.
C. D.
D
如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体B的速度为vB= ,物体上升的运动是_____(填“加速”、“减速”、“匀速”)
典例
B
v
加速
关联速度常见模型
关联速度常见模型
绳模型:vA∥=vB∥
杆模型:vA∥=vB∥
例题4.两根光滑的杆互相垂直地固定在一起,上面分别穿有一个小球,小球a、b间用一细直棒相连,如图所示.当细直棒与竖直杆夹角为θ时,则两小球实际速度大小之比为 .
tan θ
θ
分解谁? 就看谁跟绳子有夹角
5.2 运动的合成与分解
人教版(2019)物理(必修第二册)
第五单元 曲线运动
如何研究复杂的运动?
1.将放有红蜡块的玻璃管倒置在水平的电动滑轨上,向右匀速运动,观察红蜡块的运动轨迹。
实验探究
2 .将玻璃管中注满清水并倒放静置,观察红蜡块的运动轨迹
3 .将玻璃管中注满清水,并倒置在电动滑轨上,则红蜡块的运动轨迹是怎样的呢?
斜向右上方的直线运动
红蜡块同时参与了两个方向的运动,一个是水平方向的匀速直线运动,一个是竖直方向的匀速直线运动,最终实际的运动是斜向右上方的运动,故我们将水平和竖直的两个运动称为分运动;最终的实际运动称为合运动。
运动的合成与分解
01.
合运动
分运动
运动的合成
运动的分解
⑴遵循规律:平行四边形法则
⑵分解原则:通常根据运动的实际效果分解,也可以正交分解。
a
a1
a2
v1
v2
v
⑶运动的合成与分解是指 x、v、 a 的合成与分解。
A
B
x
x1
x2
位移的合成
速度的合成
加速度的合成
合运动与分运动的关系
05.
2. 独立性——各分运动独立进行,互不影响
3. 等效性——各分运动叠加起来与合运动有相同的效果
1. 等时性——分运动和合运动是同时开始和结束,时间相同。
4. 同体性——各分运动与合运动是同一个物体的运动
可以等效替代
一、合运动和分运动
定量分析:设经时间t,蜡块从O点运动到P点。
O
x
y
P
( x,y)
Vx
Vy
S
θ
x
y
水平:
竖直:
x=vxt
y=vyt
位移
大小:
方向:
轨迹
速度
大小:
方向:
结论:蜡块的运动轨
迹是条直线
例题:某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是 0.15m,自动扶梯与水平面的夹角为 30°,自动扶梯前进的速度是 0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
解:如图所示,甲在竖直方向的速度
v甲y=v甲sinθ=0.76×sin30°m/s=0.38m/s
乙在竖直方向的速度
因此v甲y >v乙,甲先到楼上。
甲比乙先到达楼上,甲上楼用了12s。
30°
v甲y
v甲
新课讲授
【典例】下列对运动的合成与分解的理解正确的是( )
A.质点的合位移一定大于两分位移
B.质点运动时,合运动的时间等于两分运动所需时间之和
C.质点的合速度等于两分速度的代数和
D.质点的合速度应为两分速度的矢量和
D
在下图所示的实验中,如果将玻璃管紧贴着黑板沿水平方向向右匀加速移动,若玻璃管内壁是光滑的,蜡块的轨迹还是一条直线吗?
蜡块的轨迹不再是一条直线,而是一条曲线。
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
互成角度的两个直线运动的合运动
不在同一直线上的两个匀速直线运动的合运动是什么运动?
匀速直线运动
v2
v1
v合
F合= 0
匀变速曲线运动。
不在同一直线上的匀速直线运动和匀变速直线运动的合运动是什么运动?
v1
F
v2
v合
思考:
1.两个匀速直线运动的合运动一定是匀速直线运动
2.一个匀速直线运动和一个匀变速直线运动的合运动一定是匀变速曲线运动
3.两个匀加速直线运动的合运动:
初速度均为零:一定是匀加速直线运动
初速度均不为零:匀变速运动(可能直线也可能曲线)
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
如图所示,在一张白纸上放置一根直尺,沿直尺的边缘放置一块直角三角板.将三角板沿直尺水平向右匀速直线运动,同时将一支铅笔从三角板直角边的最下端沿直角边向上运动,而且向上的速度越来越大,则铅笔在纸上留下的痕迹可能是( )
A. B. C. D.
C
【例题】如图所示,红蜡块能在竖直放置并装满水的玻璃管中匀速上升,若红蜡块从A点开始,沿玻璃管匀速上升的同时,使玻璃管水平向右做直线运动且玻璃管到CD处时红蜡块恰在D点,则下列说法不正确的是 ( )
A.若玻璃管匀速运动,则蜡块的轨迹为直线P
B.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线R
C.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线Q
D.若玻璃管匀减速运动,则蜡块的轨迹可能为曲线R
B
高中物理必修第二册课件
例题1
例题精选
01.
在蜡块的运动实验中,若蜡块从A点匀速上升,同时玻璃管水平向右做直线运动,蜡块最终到达C点。蜡块从A点到C点可能的4种运动轨迹如图所示,下列说法正确的
B.轨迹2中的蜡块运动时间最长
C.轨迹3也可能是玻璃管向右做匀加速直线运动形成的
D.四个轨迹中的蜡块平均速度相等
D
2.一物体在竖直平面内运动,它在竖直方向的速度时间图像和水平方向的位移时间图像分别如图甲、乙所示。关于物体运动说法正确的是( )
A.零时刻的速度为2m/s
B.加速度a=1m/s2
C.物体做匀变速直线运动
D.物体做变加速曲线运动
B
典例
小船渡河问题
1.小船参与的两个分运动
(1)船相对水的运动(即船在静水中的运动),它的方向与船头的指向相同。
(2)船随水漂流的运动,它的方向与河岸平行。
d
2.区别三个速度:水流速度v水、船在静水中的速度v船、船的实际速度(即船的合速度)v合。
1.求过河最短时间?船头冲哪个方向?
2.求过河最短位移?船头冲哪个方向?
分析小船如何渡河时间最短?
所有船速都用来过河最快。
V水
想快啊?船头朝着河岸开就对了!
最短时间:
此时位移AC:
一、小船过河(最短时间)
船头垂直于河岸
小船如何渡河才能使渡河位移最小?
位移最小等于河宽。
在非静水中开船,想办法让合运动垂直河岸方向,
船头朝向上游,船头与河岸的夹角为θ
一、小船过河(最短位移)
合运动垂直河岸方向
1.当v船>v水,
最短位移:xmin=d
渡河时间:t=
2.当v船 < v水
一、小船过河(最短位移)
船不能垂直于河岸渡河,怎样渡河位移最小?
d
v水
lmin
A
v船
θ
θ
θ
v
v船
最短位移:
渡河时间:
例、小船在宽度为100 m的河流中行驶,若它在静水中航行速度为4 m/s,水流速度为3 m/s,下列说法正确的是( )A.小船能到达出发点的正对岸B.小船在30 s时间内不可能渡过此河C.小船在河流中的航行速度大小一定为5 m/sD.若小船用最短时间渡河,则它的位移是100 m
A
5.如图所示,一条小船渡河,河宽为100m,河水流速v1=3m/s,船在静水中速度v2=4m/s,船头方向与河岸垂直,关于小船的运动,下列说法正确的是( )
A.小船的实际运动轨迹与河岸垂直
B.小船相对于河岸的速度大小为7m/s
C.小船过河后航行到了河对岸下游75m处
D.若小船行驶到河中央时,水流急速加快,则运动时间也会随之变短
4. 一船在静水中的速度为3m/s,要横渡宽为30m,流速为4m/s的河流,下列说法中不正确的是( )
A:此船能垂直到达河对岸
B:此船不可能垂直到达河对岸
C:此船相对河岸速度一定为5m/s
D:过河时间可能为15s
4. 一船在静水中的速度为3m/s,要横渡宽为30m,流速为4m/s的河流,下列说法中不正确的是( )
A:此船能垂直到达河对岸
B:此船不可能垂直到达河对岸
C:此船相对河岸速度一定为5m/s
D:过河时间可能为15s
典例
二、关联运动问题
v
θ
A
B
C
关联运动:一般是两个(或两个以上)物体通过轻绳或轻杆联系在一起。绳、杆两端所连接的物体的速度可以是不同的,但两端的物体沿绳或杆方向的速度大小一定相等
v
θ
v∥
沿绳
垂直于绳
v⊥
v船
解题技巧:
①确定合速度(实际运动)
②将实际速度分解——沿绳(杆)、垂直于绳(杆);
③作矩形——利用三角函数求解;
特点:根据两个物体沿绳(杆)方向的速度大小相等解题
1.A穿在光滑的竖直杆上,当B以速度v0匀速沿斜面体下滑时,使物体A到达如图所示位置,绳与竖直杆的夹角为θ,连接B的绳子始终与斜面体平行,则物体A上升的速度是( )
A. B.
C. D.
D
如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体B的速度为vB= ,物体上升的运动是_____(填“加速”、“减速”、“匀速”)
典例
B
v
加速
关联速度常见模型
关联速度常见模型
绳模型:vA∥=vB∥
杆模型:vA∥=vB∥
例题4.两根光滑的杆互相垂直地固定在一起,上面分别穿有一个小球,小球a、b间用一细直棒相连,如图所示.当细直棒与竖直杆夹角为θ时,则两小球实际速度大小之比为 .
tan θ
θ
分解谁? 就看谁跟绳子有夹角
