青岛版九年级数学下册第5章5.5确定二次函数的表达式同步训练题(含答案)
文档属性
| 名称 | 青岛版九年级数学下册第5章5.5确定二次函数的表达式同步训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 71.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-24 16:09:00 | ||
图片预览

文档简介
青岛版九年级数学下册第5章5.5确定二次函数的表达式同步训练题(含答案)
一.选择题(共10小题)
1.(2015 大庆校级模拟)函数y=x2+2x+1写成y=a(x﹣h)2+k的形式是( )
A.y=(x﹣1)2+2 B.y=(x﹣1)2+ C.y=(x﹣1)2﹣3 D.y=(x+2)2﹣1
2.(2013秋 泰顺县期中)抛物线y=﹣2(x﹣3)2+5的顶点坐标是( )
A.(3,﹣5) B. (﹣3,5) C. (3,5) D. (﹣3,﹣5)
3.(2015 泰安模拟)若二次函数y=ax2+bx+c的x与y的部分对应值如下表,则当x=1时,y的值为( )
x ﹣7 ﹣6 ﹣5 ﹣4 ﹣3 ﹣2
y ﹣27 ﹣13 ﹣3 3 5 3
A.5 B. ﹣3 C. ﹣13 D. ﹣27
4.(2014 长沙县校级模拟)如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B. 14 C. 8或14 D. ﹣8或﹣14
5.(2014秋 招远市期末)已知二次函数的图象经过点(﹣1,﹣5),(0,﹣4)和(1,1),则这二次函数的表达式为( )
A.y=﹣6x2+3x+4 B. y=﹣2x2+3x﹣4 C. y=x2+2x﹣4 D. y=2x2+3x﹣4
6.(2014秋 岳池县期末)顶点为(6,0),开口向下,开口的大小与函数y=x2的图象相同的抛物线所对应的函数是( )
A.y=(x+6)2 B. y=(x﹣6)2 C. y=﹣(x+6)2 D. y=﹣(x﹣6)2
7.(2014秋 伍家岗区校级期中)与y=2(x﹣1)2+3形状相同的抛物线解析式为( )
A.y=1+x2 B. y=(2x+1)2 C. y=(x﹣1)2 D. y=2x2
8.(2014秋 新疆期中)已知抛物线y=x2﹣8x+c的顶点在x轴上,则c等于( )
A.4 B. 8 C. ﹣4 D. 16
9.(2014秋 汉川市校级月考)一个二次函数的图象的顶点坐标是(2,4),且过另一点(0,﹣4),则这个二次函数的解析式为( )
A.y=﹣2(x+2)2+4 B.y=﹣2(x﹣2)2+4C.y=2(x+2)2﹣4 D. y=2(x﹣2)2﹣4
10.(2013 重庆模拟)抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 4 6 6 4 …
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+C的最大值为6;③抛物线的对称轴是;④在对称轴左侧,y随x增大而增大.其中正确有( )
A.0个 B. 1个 C. 2个 D. 3个
二.填空题(共10小题)
11.(2015 舟山)把二次函数y=x2﹣12x化为形如y=a(x﹣h)2+k的形式 .
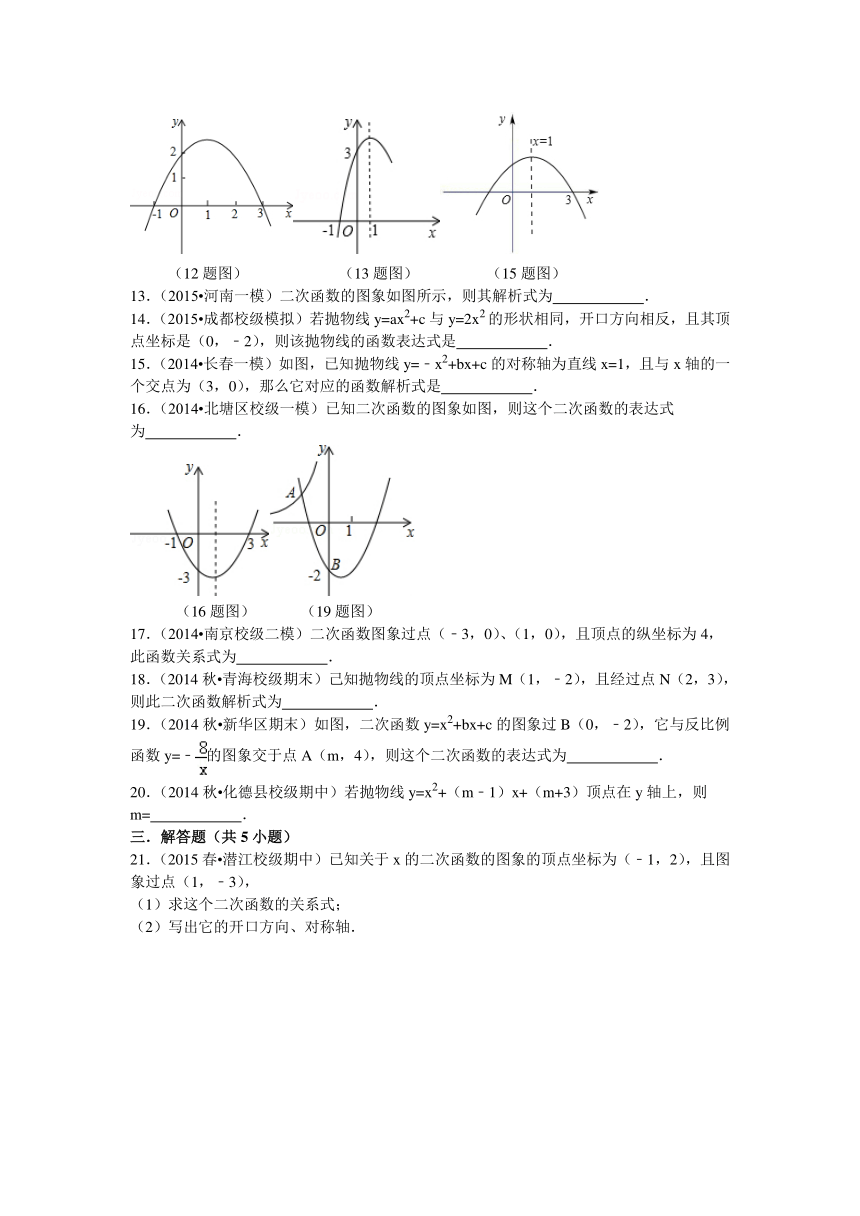
12.(2015 广陵区一模)如图,二次 ( http: / / www.21cnjy.com )函数y=ax2+bx+c的图象经过点(﹣1,0)、(3,0)和(0,2),当x=2时,y的值为 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(12题图) (13题图) (15题图)
13.(2015 河南一模)二次函数的图象如图所示,则其解析式为 .
14.(2015 成都校级模拟)若抛物线y ( http: / / www.21cnjy.com )=ax2+c与y=2x2的形状相同,开口方向相反,且其顶点坐标是(0,﹣2),则该抛物线的函数表达式是 .
15.(2014 长春一模)如图,已知抛物 ( http: / / www.21cnjy.com )线y=﹣x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是 .
16.(2014 北塘区校级一模)已知二次函数的图象如图,则这个二次函数的表达式为 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(16题图) (19题图)
17.(2014 南京校级二模)二次函数图象过点(﹣3,0)、(1,0),且顶点的纵坐标为4,此函数关系式为 .
18.(2014秋 青海校级期末)己知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),则此二次函数解析式为 .
19.(2014秋 新华区期末)如图,二次函数y=x2+bx+c的图象过B(0,﹣2),它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的表达式为 .
20.(2014秋 化德县校级期中)若抛物线y=x2+(m﹣1)x+(m+3)顶点在y轴上,则m= .
三.解答题(共5小题)
21.(2015春 潜江校级期中)已知关于x的二次函数的图象的顶点坐标为(﹣1,2),且图象过点(1,﹣3),
(1)求这个二次函数的关系式;
(2)写出它的开口方向、对称轴.
22.(2015 大庆模拟)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
( http: / / www.21cnjy.com )
23.(2014 虹口区一模)已知二次函数y=﹣﹣x+.
(1)用配方法把该二次函数的解析式化为y=a(x+m)2+k的形式;
(2)指出该二次函数图象的开口方向、顶点坐标和对称轴.
24.(2015 齐齐哈尔)如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
( http: / / www.21cnjy.com )
25.(2015 泰州)已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m、n的值;
(2)如图,一次函数y=k ( http: / / www.21cnjy.com )x+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
( http: / / www.21cnjy.com )
青岛版九年级数学下册第5章5.5确定二次函数的表达式
同步训练题参考答案
一.选择题(共10小题)
1.D 2.C 3.AD 4.C 5.D 6.D 7.D 8.D 9.B 10.D
二.填空题(共10小题)
11.y=(x-6)2-36 12.2 13.y=-x2+2x+3 14.y=-2x2-2 15.y=-x2+2x+3
16.y=x2-2x-3 17.y=-x2-2x+3 18.y=5x2-10x+3 19.y=x2-x-2 20.1
三.解答题(共5小题)
21.解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,∴AB |yP|=8,
∵AB=3+1=4,∴|yP|=4,∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,解得,x=1,
∴点P在该抛物线上滑动到(1+2,4)或(1﹣2,4)或(1,﹣4)时,满足S△PAB=8.
23.解:(1)y=﹣x2﹣x+,=﹣(x2+2x+1)++,=﹣(x+1)2+4;
(2)∵a=﹣<0,∴二次函数图象的开口向下,
顶点坐标为(﹣1,4),
对称轴为直线x=﹣1.
24.解:(1)由已知得:C(0,4),B(4,4),
把B与C坐标代入y=﹣x2+bx+c得:,解得:b=2,c=4,
则解析式为y=﹣x2+2x+4;
(2)∵y=﹣x2+2x+4=﹣(x﹣2)2+6,∴抛物线顶点坐标为(2,6),
则S四边形ABDC=S△ABC+S△BCD=×4×4+×4×2=8+4=12.
25.解:∵对称轴是经过(﹣1,0)且平行于y轴的直线,∴﹣=﹣1,∴m=2,
∵二次函数y=x2+mx+n的图象经过点P(﹣3,1),
∴9﹣3m+n=1,得出n=3m﹣8.
∴n=3m﹣8=﹣2;
(2)∵m=2,n=﹣2,∴二次函数为y=x2+2x﹣2,
作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,∴=,
∵P(﹣3,1),∴PC=1,
∵PA:PB=1:5,∴=,∴BD=6,∴B的纵坐标为6,
代入二次函数为y=x2+2x﹣2得,6=x2+2x﹣2,解得x1=2,x2=﹣4(舍去),
∴B(2,6),∴,解得,
∴一次函数的表达式为y=x+4.
( http: / / www.21cnjy.com )
一.选择题(共10小题)
1.(2015 大庆校级模拟)函数y=x2+2x+1写成y=a(x﹣h)2+k的形式是( )
A.y=(x﹣1)2+2 B.y=(x﹣1)2+ C.y=(x﹣1)2﹣3 D.y=(x+2)2﹣1
2.(2013秋 泰顺县期中)抛物线y=﹣2(x﹣3)2+5的顶点坐标是( )
A.(3,﹣5) B. (﹣3,5) C. (3,5) D. (﹣3,﹣5)
3.(2015 泰安模拟)若二次函数y=ax2+bx+c的x与y的部分对应值如下表,则当x=1时,y的值为( )
x ﹣7 ﹣6 ﹣5 ﹣4 ﹣3 ﹣2
y ﹣27 ﹣13 ﹣3 3 5 3
A.5 B. ﹣3 C. ﹣13 D. ﹣27
4.(2014 长沙县校级模拟)如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B. 14 C. 8或14 D. ﹣8或﹣14
5.(2014秋 招远市期末)已知二次函数的图象经过点(﹣1,﹣5),(0,﹣4)和(1,1),则这二次函数的表达式为( )
A.y=﹣6x2+3x+4 B. y=﹣2x2+3x﹣4 C. y=x2+2x﹣4 D. y=2x2+3x﹣4
6.(2014秋 岳池县期末)顶点为(6,0),开口向下,开口的大小与函数y=x2的图象相同的抛物线所对应的函数是( )
A.y=(x+6)2 B. y=(x﹣6)2 C. y=﹣(x+6)2 D. y=﹣(x﹣6)2
7.(2014秋 伍家岗区校级期中)与y=2(x﹣1)2+3形状相同的抛物线解析式为( )
A.y=1+x2 B. y=(2x+1)2 C. y=(x﹣1)2 D. y=2x2
8.(2014秋 新疆期中)已知抛物线y=x2﹣8x+c的顶点在x轴上,则c等于( )
A.4 B. 8 C. ﹣4 D. 16
9.(2014秋 汉川市校级月考)一个二次函数的图象的顶点坐标是(2,4),且过另一点(0,﹣4),则这个二次函数的解析式为( )
A.y=﹣2(x+2)2+4 B.y=﹣2(x﹣2)2+4C.y=2(x+2)2﹣4 D. y=2(x﹣2)2﹣4
10.(2013 重庆模拟)抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 4 6 6 4 …
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+C的最大值为6;③抛物线的对称轴是;④在对称轴左侧,y随x增大而增大.其中正确有( )
A.0个 B. 1个 C. 2个 D. 3个
二.填空题(共10小题)
11.(2015 舟山)把二次函数y=x2﹣12x化为形如y=a(x﹣h)2+k的形式 .
12.(2015 广陵区一模)如图,二次 ( http: / / www.21cnjy.com )函数y=ax2+bx+c的图象经过点(﹣1,0)、(3,0)和(0,2),当x=2时,y的值为 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(12题图) (13题图) (15题图)
13.(2015 河南一模)二次函数的图象如图所示,则其解析式为 .
14.(2015 成都校级模拟)若抛物线y ( http: / / www.21cnjy.com )=ax2+c与y=2x2的形状相同,开口方向相反,且其顶点坐标是(0,﹣2),则该抛物线的函数表达式是 .
15.(2014 长春一模)如图,已知抛物 ( http: / / www.21cnjy.com )线y=﹣x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是 .
16.(2014 北塘区校级一模)已知二次函数的图象如图,则这个二次函数的表达式为 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(16题图) (19题图)
17.(2014 南京校级二模)二次函数图象过点(﹣3,0)、(1,0),且顶点的纵坐标为4,此函数关系式为 .
18.(2014秋 青海校级期末)己知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),则此二次函数解析式为 .
19.(2014秋 新华区期末)如图,二次函数y=x2+bx+c的图象过B(0,﹣2),它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的表达式为 .
20.(2014秋 化德县校级期中)若抛物线y=x2+(m﹣1)x+(m+3)顶点在y轴上,则m= .
三.解答题(共5小题)
21.(2015春 潜江校级期中)已知关于x的二次函数的图象的顶点坐标为(﹣1,2),且图象过点(1,﹣3),
(1)求这个二次函数的关系式;
(2)写出它的开口方向、对称轴.
22.(2015 大庆模拟)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
( http: / / www.21cnjy.com )
23.(2014 虹口区一模)已知二次函数y=﹣﹣x+.
(1)用配方法把该二次函数的解析式化为y=a(x+m)2+k的形式;
(2)指出该二次函数图象的开口方向、顶点坐标和对称轴.
24.(2015 齐齐哈尔)如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
( http: / / www.21cnjy.com )
25.(2015 泰州)已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m、n的值;
(2)如图,一次函数y=k ( http: / / www.21cnjy.com )x+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
( http: / / www.21cnjy.com )
青岛版九年级数学下册第5章5.5确定二次函数的表达式
同步训练题参考答案
一.选择题(共10小题)
1.D 2.C 3.AD 4.C 5.D 6.D 7.D 8.D 9.B 10.D
二.填空题(共10小题)
11.y=(x-6)2-36 12.2 13.y=-x2+2x+3 14.y=-2x2-2 15.y=-x2+2x+3
16.y=x2-2x-3 17.y=-x2-2x+3 18.y=5x2-10x+3 19.y=x2-x-2 20.1
三.解答题(共5小题)
21.解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,∴AB |yP|=8,
∵AB=3+1=4,∴|yP|=4,∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,解得,x=1,
∴点P在该抛物线上滑动到(1+2,4)或(1﹣2,4)或(1,﹣4)时,满足S△PAB=8.
23.解:(1)y=﹣x2﹣x+,=﹣(x2+2x+1)++,=﹣(x+1)2+4;
(2)∵a=﹣<0,∴二次函数图象的开口向下,
顶点坐标为(﹣1,4),
对称轴为直线x=﹣1.
24.解:(1)由已知得:C(0,4),B(4,4),
把B与C坐标代入y=﹣x2+bx+c得:,解得:b=2,c=4,
则解析式为y=﹣x2+2x+4;
(2)∵y=﹣x2+2x+4=﹣(x﹣2)2+6,∴抛物线顶点坐标为(2,6),
则S四边形ABDC=S△ABC+S△BCD=×4×4+×4×2=8+4=12.
25.解:∵对称轴是经过(﹣1,0)且平行于y轴的直线,∴﹣=﹣1,∴m=2,
∵二次函数y=x2+mx+n的图象经过点P(﹣3,1),
∴9﹣3m+n=1,得出n=3m﹣8.
∴n=3m﹣8=﹣2;
(2)∵m=2,n=﹣2,∴二次函数为y=x2+2x﹣2,
作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,∴=,
∵P(﹣3,1),∴PC=1,
∵PA:PB=1:5,∴=,∴BD=6,∴B的纵坐标为6,
代入二次函数为y=x2+2x﹣2得,6=x2+2x﹣2,解得x1=2,x2=﹣4(舍去),
∴B(2,6),∴,解得,
∴一次函数的表达式为y=x+4.
( http: / / www.21cnjy.com )
