人教版小学数学五年级下册《1、2单元晨读熟记内容》课件(共31张PPT)
文档属性
| 名称 | 人教版小学数学五年级下册《1、2单元晨读熟记内容》课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 22:30:20 | ||
图片预览










文档简介
(共31张PPT)
观察物体
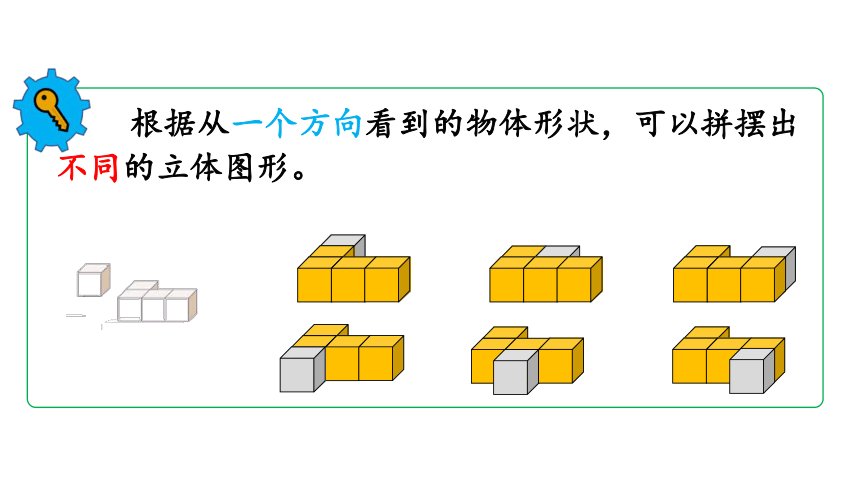
1.根据从一个方向观察到的图形,用同样的
小正方体可以摆出多种不同的几何体。
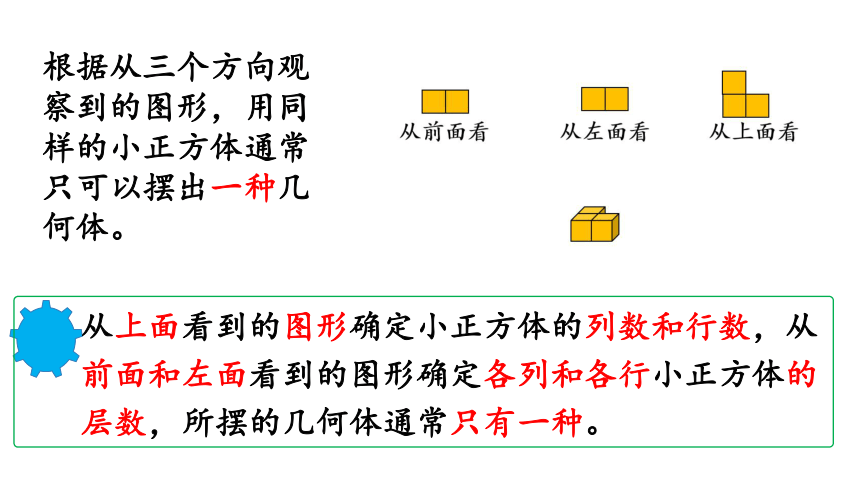
2.根据从三个方向观察到的图形,用同样的
小正方体通常只可以摆出一种几何体。
根据从一个方向看到的物体形状,可以拼摆出不同的立体图形。
从上面看到的图形确定小正方体的列数和行数,从前面和左面看到的图形确定各列和各行小正方体的层数,所摆的几何体通常只有一种。
根据从三个方向观察到的图形,用同样的小正方体通常只可以摆出一种几何体。
添加小正方体后从同一方向看到的图形不变的摆放要领:
从前面看不变 添加的小正方体摆在已有小正方体的前面或后面;
从侧面看不变 添加的小正方体摆在已有小正方体的左面或右面;
从上面看不变 添加的小正方体摆在已有小正方体的上面。
如果a÷b=c(a,b,c都是不为0的自然数),那么b和c就是a的因数,a就是b和c的倍数。
因数和倍数的关系是什么?
为了方便,在研究因数和倍数的时候,我们所指的数是自然数(一般不包括0)。
如果a×b=c(a,b,c都是不为0的自然数),那么a和b就是c的因数,c就是a和b的倍数。
因数和倍数是相互依存的。
因数和倍数的关系是什么?
怎样找一个数的因数?
用除法找:用这个数除以从1开始的整数,商是整数且没有余数,那么除数和商都是这个数的因数。
用乘法找:也可以从1开始,看看哪两个整数的乘积是这个数,那么这两个整数就都是这个数的因数。
一个数的因数的个数是有限的,它的最小因数是1,最大因数是它本身;
一个数的倍数的个数是无限的,它的最小倍数是它本身,没有最大倍数。
因数和倍数的特征是什么?
怎样找一个数的倍数?
也可以用这个数分别乘1,2,3,…,所得的积都是这个数的倍数。
整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。
奇数、偶数的意义
个位上是0,2,4,6或8的数,都是2的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
个位上是0或5的数,都是5的倍数。
2、3、5的倍数
质数和合数
1. 一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数)。
2.一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
3.1既不是质数,也不是合数。2是最小的质数,4是最小的合数。
☆判断一个数是合数还是质数的方法:
先找出这个数的因数,再根据质数和合数的定义去判断。
1既不是质数也不是合数。
☆奇数与偶数的和的奇偶性:
奇数+偶数=奇数 奇数+奇数=偶数
偶数+偶数=偶数
奇数个奇数相加的和是奇数。
偶数个奇数相加的和是偶数。
不管多少个偶数相加的和都是偶数。
质数中,除2是偶数外,其他都是奇数。
你知道吗?
完全数
6的因数有1,2,3,6,这几个因数的关系是:1+2+3=6。像6这样,等于除了它自身以外的全部因数之和的数,叫作完全数。
28也是完全数,而8则不是,因为1+2+4≠8。完全数非常稀少,截至2021年,人们一共找出了51个完全数,其中较小的有6,28,496,8128等。
完全数还有一个有趣的性质,它们都能写成连续自然数之和。不信你可以试试看。
教材第8页
你知道吗?
哥德巴赫猜想
教材第17页
从上面第6题的游戏中我们可以看到:4=2+2,6=3+3,8=5+3,10=7+3,12=7+5,14=11+3……那么,是不是所有大于2的偶数,都可以表示为两个质数的和呢?
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。哥德巴赫猜想看似简单,但要证明却非常困难,因而成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。
世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
(1)1是1,2,3,…的因数。
1是所有非零自然数的因数。
(2)8的倍数只有16,24,32,40,48。
一个数的倍数的个数是无限的。
(3)因为36÷9=4,所以36是9的倍数。
36除以9得到的商是整数且没有余数。
(4)5.7是3的倍数。
5.7不是自然数。
5. 判断下面的说法是否正确,并说一说你的理由。
不正确
不正确
正确
正确
【教材第7页第5题】
8.(1)14、21都是7的倍数,14与21的和是7的倍数吗?
(2)27、18都是9的倍数,27与18的差是9的倍数吗?
通过这两个小题,你有什么发现?你能再举几个例子验
证你的发现吗?
(1)14+21=35 35÷7=5
所以14与21的和是7的倍数。
(2)27-18=9 9÷9=1
所以27与18的差是9的倍数。
我发现:如果两个数都是一个数的倍数,那么这两个数的和或差也是这个数的倍数。
【教材第8页第8题】
7. 妈妈在花店买了一些马蹄莲和郁金香,店员说妈妈应付87元。按照下面的价格计算,店员说得对吗?
马蹄莲单价为10元,买马蹄莲的钱数是5的倍数;郁金香单价为5元,买郁金香的钱数是5的倍数。所以买马蹄莲和郁金香的总钱数是5的倍数。87不是5的倍数,所以店员说得不对。
【教材第12页第7题】
马蹄莲
10元/枝
玫瑰
3元/枝
郁金香
5元/枝
8. 判断下面的说法是否正确,并说一说你的理由。
(1)个位上是3,6,9的数,都是3的倍数。
(2)个位上是1,3,5,7,9的数,都是奇数。
(3)在全部整数里,不是奇数就是偶数。
不正确
正确
正确
①13,16,19都不是3的倍数。
②一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【教材第12页第8题】
只看个位,不能判断一个数是不是4 的倍数。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
(2)*只看个位,能否判断一个数是不是4的倍数?应该怎样判断?
末尾两位数是4的倍数的数就是4的倍数。
【教材第12页第11题】
12.(1)既是2和5的倍数,又是3的倍数的最小两
位数是_____。
(2)既是2的倍数,又是3的倍数的最小三位
数是_____ ,最大三位数是_____ 。
30
102
996
【教材第13页第12题】
1.判断下面的说法是否正确,并说一说你的理由。
(1)所有的奇数都是质数。
(2)所有的偶数都是合数。
不正确。例如9、15都是奇数,除了1和它本身,还有其他的因数。
不正确。2是偶数,但不是合数。
教材第16页第1题
练习巩固
(教材第16~17页练习四)
(3)在1,2,3,4,5,…中,除了质数以外都是合数。
教材第16页第1题
练习巩固
(教材第16~17页练习四)
(4)两个质数的和是偶数。
不正确。1既不是质数,也不是合数。
不正确。如:2+3=5,5是奇数,不是偶数。
1.判断下面的说法是否正确,并说一说你的理由。
7.探索6的倍数的特征,并记录你探索的过程和
结果。
6×1= 6
6×2=12
6×3=18
6×4=24
6×5=30
6×6=36
6×7=42
6×8=48
6×9=54
…
结果:6的倍数的个位数是0,2,4,6或8,且各位上数的和是3的倍数。
6
3
9
6
3
9
6
3
9
【教材第17页第7题】
观察物体
1.根据从一个方向观察到的图形,用同样的
小正方体可以摆出多种不同的几何体。
2.根据从三个方向观察到的图形,用同样的
小正方体通常只可以摆出一种几何体。
根据从一个方向看到的物体形状,可以拼摆出不同的立体图形。
从上面看到的图形确定小正方体的列数和行数,从前面和左面看到的图形确定各列和各行小正方体的层数,所摆的几何体通常只有一种。
根据从三个方向观察到的图形,用同样的小正方体通常只可以摆出一种几何体。
添加小正方体后从同一方向看到的图形不变的摆放要领:
从前面看不变 添加的小正方体摆在已有小正方体的前面或后面;
从侧面看不变 添加的小正方体摆在已有小正方体的左面或右面;
从上面看不变 添加的小正方体摆在已有小正方体的上面。
如果a÷b=c(a,b,c都是不为0的自然数),那么b和c就是a的因数,a就是b和c的倍数。
因数和倍数的关系是什么?
为了方便,在研究因数和倍数的时候,我们所指的数是自然数(一般不包括0)。
如果a×b=c(a,b,c都是不为0的自然数),那么a和b就是c的因数,c就是a和b的倍数。
因数和倍数是相互依存的。
因数和倍数的关系是什么?
怎样找一个数的因数?
用除法找:用这个数除以从1开始的整数,商是整数且没有余数,那么除数和商都是这个数的因数。
用乘法找:也可以从1开始,看看哪两个整数的乘积是这个数,那么这两个整数就都是这个数的因数。
一个数的因数的个数是有限的,它的最小因数是1,最大因数是它本身;
一个数的倍数的个数是无限的,它的最小倍数是它本身,没有最大倍数。
因数和倍数的特征是什么?
怎样找一个数的倍数?
也可以用这个数分别乘1,2,3,…,所得的积都是这个数的倍数。
整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。
奇数、偶数的意义
个位上是0,2,4,6或8的数,都是2的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
个位上是0或5的数,都是5的倍数。
2、3、5的倍数
质数和合数
1. 一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数)。
2.一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
3.1既不是质数,也不是合数。2是最小的质数,4是最小的合数。
☆判断一个数是合数还是质数的方法:
先找出这个数的因数,再根据质数和合数的定义去判断。
1既不是质数也不是合数。
☆奇数与偶数的和的奇偶性:
奇数+偶数=奇数 奇数+奇数=偶数
偶数+偶数=偶数
奇数个奇数相加的和是奇数。
偶数个奇数相加的和是偶数。
不管多少个偶数相加的和都是偶数。
质数中,除2是偶数外,其他都是奇数。
你知道吗?
完全数
6的因数有1,2,3,6,这几个因数的关系是:1+2+3=6。像6这样,等于除了它自身以外的全部因数之和的数,叫作完全数。
28也是完全数,而8则不是,因为1+2+4≠8。完全数非常稀少,截至2021年,人们一共找出了51个完全数,其中较小的有6,28,496,8128等。
完全数还有一个有趣的性质,它们都能写成连续自然数之和。不信你可以试试看。
教材第8页
你知道吗?
哥德巴赫猜想
教材第17页
从上面第6题的游戏中我们可以看到:4=2+2,6=3+3,8=5+3,10=7+3,12=7+5,14=11+3……那么,是不是所有大于2的偶数,都可以表示为两个质数的和呢?
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。哥德巴赫猜想看似简单,但要证明却非常困难,因而成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。
世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
(1)1是1,2,3,…的因数。
1是所有非零自然数的因数。
(2)8的倍数只有16,24,32,40,48。
一个数的倍数的个数是无限的。
(3)因为36÷9=4,所以36是9的倍数。
36除以9得到的商是整数且没有余数。
(4)5.7是3的倍数。
5.7不是自然数。
5. 判断下面的说法是否正确,并说一说你的理由。
不正确
不正确
正确
正确
【教材第7页第5题】
8.(1)14、21都是7的倍数,14与21的和是7的倍数吗?
(2)27、18都是9的倍数,27与18的差是9的倍数吗?
通过这两个小题,你有什么发现?你能再举几个例子验
证你的发现吗?
(1)14+21=35 35÷7=5
所以14与21的和是7的倍数。
(2)27-18=9 9÷9=1
所以27与18的差是9的倍数。
我发现:如果两个数都是一个数的倍数,那么这两个数的和或差也是这个数的倍数。
【教材第8页第8题】
7. 妈妈在花店买了一些马蹄莲和郁金香,店员说妈妈应付87元。按照下面的价格计算,店员说得对吗?
马蹄莲单价为10元,买马蹄莲的钱数是5的倍数;郁金香单价为5元,买郁金香的钱数是5的倍数。所以买马蹄莲和郁金香的总钱数是5的倍数。87不是5的倍数,所以店员说得不对。
【教材第12页第7题】
马蹄莲
10元/枝
玫瑰
3元/枝
郁金香
5元/枝
8. 判断下面的说法是否正确,并说一说你的理由。
(1)个位上是3,6,9的数,都是3的倍数。
(2)个位上是1,3,5,7,9的数,都是奇数。
(3)在全部整数里,不是奇数就是偶数。
不正确
正确
正确
①13,16,19都不是3的倍数。
②一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【教材第12页第8题】
只看个位,不能判断一个数是不是4 的倍数。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
(2)*只看个位,能否判断一个数是不是4的倍数?应该怎样判断?
末尾两位数是4的倍数的数就是4的倍数。
【教材第12页第11题】
12.(1)既是2和5的倍数,又是3的倍数的最小两
位数是_____。
(2)既是2的倍数,又是3的倍数的最小三位
数是_____ ,最大三位数是_____ 。
30
102
996
【教材第13页第12题】
1.判断下面的说法是否正确,并说一说你的理由。
(1)所有的奇数都是质数。
(2)所有的偶数都是合数。
不正确。例如9、15都是奇数,除了1和它本身,还有其他的因数。
不正确。2是偶数,但不是合数。
教材第16页第1题
练习巩固
(教材第16~17页练习四)
(3)在1,2,3,4,5,…中,除了质数以外都是合数。
教材第16页第1题
练习巩固
(教材第16~17页练习四)
(4)两个质数的和是偶数。
不正确。1既不是质数,也不是合数。
不正确。如:2+3=5,5是奇数,不是偶数。
1.判断下面的说法是否正确,并说一说你的理由。
7.探索6的倍数的特征,并记录你探索的过程和
结果。
6×1= 6
6×2=12
6×3=18
6×4=24
6×5=30
6×6=36
6×7=42
6×8=48
6×9=54
…
结果:6的倍数的个位数是0,2,4,6或8,且各位上数的和是3的倍数。
6
3
9
6
3
9
6
3
9
【教材第17页第7题】
