3.1《列方程解决问题(三)》(第三课时)教学课件(共26张PPT)五年级 数学下册 沪教版
文档属性
| 名称 | 3.1《列方程解决问题(三)》(第三课时)教学课件(共26张PPT)五年级 数学下册 沪教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 15:21:26 | ||
图片预览






文档简介
(共26张PPT)
列方程解决问题(三)
小学数学·五年级(下)
沪教版·第三单元
第三课时
在理解题意的基础上寻找等量关系,初步学习相遇问题的列方程解应用题的一般方法。
让学生尝试着画线段图。
联系生活,以学生互动为主线,以说促思,让学生在探索、认识相遇的过程中理解运用等量关系的解决问题,帮助学生建立行程问题的观念。
重
能根据题意找到正确的等量关系,并出列方程求出解。
能读懂题意并找出等量关系。
沪宁高速公路全长约270千米,一辆轿车和一辆客车分别从上海和南京两地同时出发,相向而行。轿车平均每小时行100千米,客车平均每小时行80千米,经过几小时两车在途中相遇?
知识点一:列方程解决简单的“相遇问题”
问题
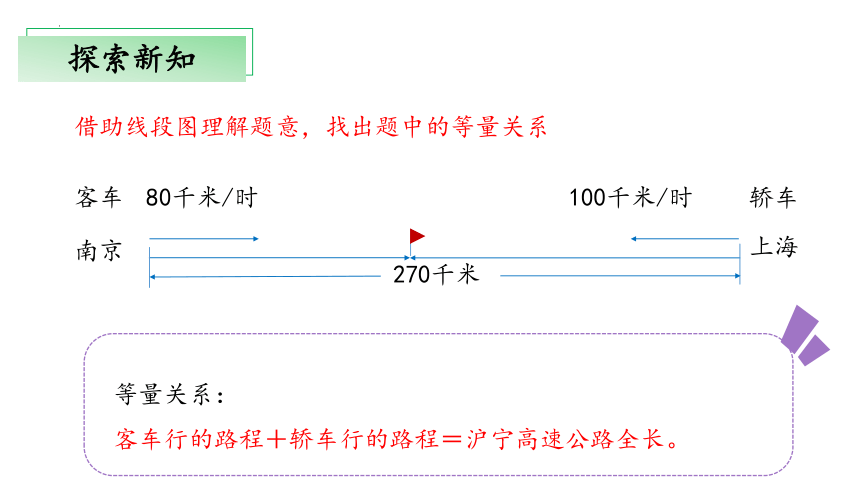
借助线段图理解题意,找出题中的等量关系
等量关系:
客车行的路程+轿车行的路程=沪宁高速公路全长。
客车
南京
轿车
上海
80千米/时
100千米/时
270千米
根据等量关系列方程解决问题
客车行的路程+轿车行的路程=沪宁高速公路全长
解:设经过x小时两车在途中相遇。
80x+100x=270
180x=270
x=1.5
检验:把x=1.5代入原方程,
方程左边=80×1.5+100×1.5=270,
方程右边=270,
方程左边=方程右边,
所以x=1.5是原方程的解。
答:经过1.5小时两车在途中相遇。
“相遇问题”中的等量关系:
甲行的路程+乙行的路程=相距的路程。
一辆客车和一辆轿车先后从上海出发去南京,客车先行50千米后轿车出发,客车平均每小时行80千米,轿车平均每小时行100千米。轿车几小时后追上客车?
知识点二:列方程解决简单的“追及问题”
问题
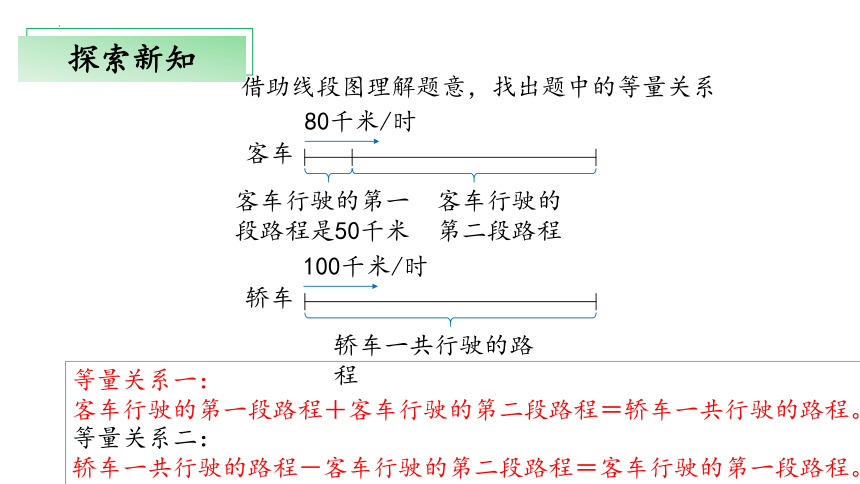
借助线段图理解题意,找出题中的等量关系
等量关系一:
客车行驶的第一段路程+客车行驶的第二段路程=轿车一共行驶的路程。
等量关系二:
轿车一共行驶的路程-客车行驶的第二段路程=客车行驶的第一段路程。
客车
轿车
80千米/时
客车行驶的第二段路程
客车行驶的第一段路程是50千米
100千米/时
轿车一共行驶的路程
根据等量关系一列方程解决问题
客车行驶的第一段路程+客车行驶的第二段路程=轿车一共行驶的路程
解:设轿车x小时后追上客车。
50+80x=100x
100x-80x=50
x=2.5
20x=50
答:轿车2.5小时后追上客车。
根据等量关系二列方程解决问题
轿车一共行驶的路程-客车行驶的第二段路程=客车行驶的第一段路程
解:设轿车x小时后追上客车。
100-80x=50
x=2.5
20x=50
答:轿车2.5小时后追上客车。
1、小胖上学时忘了带文具盒,爸爸发现时,小胖刚好离家512米,正以72米/分的速度走向学校,爸爸骑车以200米/分的速度追赶,爸爸几分钟后在途中追上小胖?
解:设爸爸x分钟后在途中追上小胖.
(200 – 72) x = 512 ,
128 x = 512 ,
x = 4 .
答:爸爸4分钟后在途中追上小胖.
(爸爸的速度 - 小胖的速度)×追及的时间=追及的路程 .
2、小丁丁和小巧跑步锻炼身体,小巧跑出200米后小丁丁从起点出发,小丁丁平均每分钟跑170米,5分钟后在途中追上小巧,小巧平均每分钟跑多少米?
解:设小巧平均每分钟跑x米.
200 + 5 x = 170×5 ,
200 + 5 x = 850 ,
5 x = 650 ,
x = 130 .
答:小巧平均每分钟跑130米.
小巧跑的第一段路程+小巧跑的第二段路程=小丁丁一共跑的路程 .
总 结
“追及问题”中的等量关系:
追及时间=追及距离÷速度差、
追及距离=速度差×追及时间、
速度差=追及距离÷追及时间。
学校给一批新入学的学生分配宿舍。如果每个房间住4人,那么房间正好住满;如果每个房间住6人,那么正好空出5个房间。学生宿舍有多少间?住宿学生有多少人?
知识点三:列方程解决简单的“盈亏问题”
问题
理解题意,找出题中的等量关系
等量关系:“每间住4人”的总人数=“每间住6人”的总人数
两次分配的房间数不同,但是住宿学生的总人数相同
根据等量关系列方程解决问题
“每间住4人”的总人数=“每间住6人”的总人数
解:设学生宿舍有x间,则住宿学生有4x人。
4x=6(x-5)
4x=6x-30
4x=4×15=60或6(x-5)=6×(15-5)=60
x=15
2x=30
答:学生宿舍有15间,住宿学生有60人。
6x-4x=30
1. 五年级一个班的学生去湖边坐游船.如果每条船坐12人,那么租的这些船正好坐满;如果每条船坐9人,那么需要多租一条船. 原来要租多少条船?这个班一共有学生多少人?
“每条船坐12人”的总人数=“每条船坐9人”的总人数.
解:设原来要租x条船,则这个班一共有学生12 x人.
12 x = 9( x + 1),
12 x = 9 x + 9 ,
12 x -9 x = 9 , 12 x = 12×3 = 36.
3 x = 9 , 答:原来要租3条船,
x = 3 . 这个班一共有学生36人.
( )
6 x = 4x + 48 , 6 x = 6×24 = 144.
6 x -4 x = 48 ,
2 x = 48 , 答:学生宿舍有24间,
x = 24 . 住宿学生有144人.
2. 一所学校给住宿学生分配宿舍. 如果每间宿舍住6人,那么正好住满;如果每间宿舍住4人,那么正好缺12间宿舍,学生宿舍有多少间?住宿学生有多少人?
“每间住6人”的总人数=“每间住4人”的总人数.
解:设学生宿舍有x间,则住宿学生有6 x人.
6 x = 4
( x +12),
( x -12)
1.列方程解决“盈亏问题”时,应根据总数不变建立等量关系。
2.列方程解决问题的一般步骤是:
(1)用字母表示未知数,并根据题意,用未知数来表示相关的量;
(2)找出未知量与已知量之间的等量关系,并列出方程;
(3)解方程;
(4)检验并写出答句。
两个城市相距255千米。甲、乙两辆汽车同时从两个城市出发,相向而行。如果甲车的速度是42千米/时,3小时后两车相遇。求乙车的速度。
甲车
乙车
255千米
42千米/时
?千米/时
甲行的路程
乙行的路程
甲路程+乙路程=总路程
解:设乙车的速度是X千米/时。
42×3+3x=255
速度和×时间=总路程
解:设乙车的速度是X千米/时。
3(42+X)=255
相遇问题
42×3
3x
快车和慢车同时从相距720千米的两地出发相向而行,4小时相遇。已知快车的速度是慢车的1.5倍,求快车的速度?
快车的路程+慢车的路程=总路程
解:设慢车的速度是X千米/时,则快车的速度是1.5X千米/时。。
4 1.5X+4X=720
6X+4X=720
10X=720
X=72
慢车的速度
1.5X=1.5×72=108
快车的速度
相遇问题
甲乙两个工程队合修一条长24千米的公路,甲队每天修0.32千米,比乙队每天少修0.11千米。两队从两端同时开工,几天后可以修好这条公路?
甲修的+乙修的=一共修的
解:设X天以后可以修好这条公路。
0.32X+(0.32+0.11)X=24
或(0.32+0.32+0.11)X=24
相遇问题
李老师带一笔钱去买文具. 如果买单价为8元的钢笔,正好用完;如果改买单价为6元的圆珠笔,则可以多买4支,钱也正好用完. 钢笔可以买多少支?李老师一共带了多少元?
解:设钢笔可以买x支,李老师一共带了8 x元. 下面方程正确的是( ).
A. 8 x = 6 x + 4 B. 8 x = 6( x + 4)
C. 8 x = 6 x - 4 D. 8 x = 6( x - 4)
B
选一选
作业:
练一练:列方程解应用题
1、小亚和小巧同时从相距960米的两地出发,相向而行,小亚平均每分钟走58米,小巧平均每分钟走62米,几分钟后两人在途中相遇?
2、两个城市之间的路程为405千米,一辆客车和一辆货车同时从这两个城市出发,相向而行,客车平均每小时行44千米,4.5小时后两车相遇,货车平均每小时行多少千米?
Thank you!
列方程解决问题(三)
小学数学·五年级(下)
沪教版·第三单元
第三课时
在理解题意的基础上寻找等量关系,初步学习相遇问题的列方程解应用题的一般方法。
让学生尝试着画线段图。
联系生活,以学生互动为主线,以说促思,让学生在探索、认识相遇的过程中理解运用等量关系的解决问题,帮助学生建立行程问题的观念。
重
能根据题意找到正确的等量关系,并出列方程求出解。
能读懂题意并找出等量关系。
沪宁高速公路全长约270千米,一辆轿车和一辆客车分别从上海和南京两地同时出发,相向而行。轿车平均每小时行100千米,客车平均每小时行80千米,经过几小时两车在途中相遇?
知识点一:列方程解决简单的“相遇问题”
问题
借助线段图理解题意,找出题中的等量关系
等量关系:
客车行的路程+轿车行的路程=沪宁高速公路全长。
客车
南京
轿车
上海
80千米/时
100千米/时
270千米
根据等量关系列方程解决问题
客车行的路程+轿车行的路程=沪宁高速公路全长
解:设经过x小时两车在途中相遇。
80x+100x=270
180x=270
x=1.5
检验:把x=1.5代入原方程,
方程左边=80×1.5+100×1.5=270,
方程右边=270,
方程左边=方程右边,
所以x=1.5是原方程的解。
答:经过1.5小时两车在途中相遇。
“相遇问题”中的等量关系:
甲行的路程+乙行的路程=相距的路程。
一辆客车和一辆轿车先后从上海出发去南京,客车先行50千米后轿车出发,客车平均每小时行80千米,轿车平均每小时行100千米。轿车几小时后追上客车?
知识点二:列方程解决简单的“追及问题”
问题
借助线段图理解题意,找出题中的等量关系
等量关系一:
客车行驶的第一段路程+客车行驶的第二段路程=轿车一共行驶的路程。
等量关系二:
轿车一共行驶的路程-客车行驶的第二段路程=客车行驶的第一段路程。
客车
轿车
80千米/时
客车行驶的第二段路程
客车行驶的第一段路程是50千米
100千米/时
轿车一共行驶的路程
根据等量关系一列方程解决问题
客车行驶的第一段路程+客车行驶的第二段路程=轿车一共行驶的路程
解:设轿车x小时后追上客车。
50+80x=100x
100x-80x=50
x=2.5
20x=50
答:轿车2.5小时后追上客车。
根据等量关系二列方程解决问题
轿车一共行驶的路程-客车行驶的第二段路程=客车行驶的第一段路程
解:设轿车x小时后追上客车。
100-80x=50
x=2.5
20x=50
答:轿车2.5小时后追上客车。
1、小胖上学时忘了带文具盒,爸爸发现时,小胖刚好离家512米,正以72米/分的速度走向学校,爸爸骑车以200米/分的速度追赶,爸爸几分钟后在途中追上小胖?
解:设爸爸x分钟后在途中追上小胖.
(200 – 72) x = 512 ,
128 x = 512 ,
x = 4 .
答:爸爸4分钟后在途中追上小胖.
(爸爸的速度 - 小胖的速度)×追及的时间=追及的路程 .
2、小丁丁和小巧跑步锻炼身体,小巧跑出200米后小丁丁从起点出发,小丁丁平均每分钟跑170米,5分钟后在途中追上小巧,小巧平均每分钟跑多少米?
解:设小巧平均每分钟跑x米.
200 + 5 x = 170×5 ,
200 + 5 x = 850 ,
5 x = 650 ,
x = 130 .
答:小巧平均每分钟跑130米.
小巧跑的第一段路程+小巧跑的第二段路程=小丁丁一共跑的路程 .
总 结
“追及问题”中的等量关系:
追及时间=追及距离÷速度差、
追及距离=速度差×追及时间、
速度差=追及距离÷追及时间。
学校给一批新入学的学生分配宿舍。如果每个房间住4人,那么房间正好住满;如果每个房间住6人,那么正好空出5个房间。学生宿舍有多少间?住宿学生有多少人?
知识点三:列方程解决简单的“盈亏问题”
问题
理解题意,找出题中的等量关系
等量关系:“每间住4人”的总人数=“每间住6人”的总人数
两次分配的房间数不同,但是住宿学生的总人数相同
根据等量关系列方程解决问题
“每间住4人”的总人数=“每间住6人”的总人数
解:设学生宿舍有x间,则住宿学生有4x人。
4x=6(x-5)
4x=6x-30
4x=4×15=60或6(x-5)=6×(15-5)=60
x=15
2x=30
答:学生宿舍有15间,住宿学生有60人。
6x-4x=30
1. 五年级一个班的学生去湖边坐游船.如果每条船坐12人,那么租的这些船正好坐满;如果每条船坐9人,那么需要多租一条船. 原来要租多少条船?这个班一共有学生多少人?
“每条船坐12人”的总人数=“每条船坐9人”的总人数.
解:设原来要租x条船,则这个班一共有学生12 x人.
12 x = 9( x + 1),
12 x = 9 x + 9 ,
12 x -9 x = 9 , 12 x = 12×3 = 36.
3 x = 9 , 答:原来要租3条船,
x = 3 . 这个班一共有学生36人.
( )
6 x = 4x + 48 , 6 x = 6×24 = 144.
6 x -4 x = 48 ,
2 x = 48 , 答:学生宿舍有24间,
x = 24 . 住宿学生有144人.
2. 一所学校给住宿学生分配宿舍. 如果每间宿舍住6人,那么正好住满;如果每间宿舍住4人,那么正好缺12间宿舍,学生宿舍有多少间?住宿学生有多少人?
“每间住6人”的总人数=“每间住4人”的总人数.
解:设学生宿舍有x间,则住宿学生有6 x人.
6 x = 4
( x +12),
( x -12)
1.列方程解决“盈亏问题”时,应根据总数不变建立等量关系。
2.列方程解决问题的一般步骤是:
(1)用字母表示未知数,并根据题意,用未知数来表示相关的量;
(2)找出未知量与已知量之间的等量关系,并列出方程;
(3)解方程;
(4)检验并写出答句。
两个城市相距255千米。甲、乙两辆汽车同时从两个城市出发,相向而行。如果甲车的速度是42千米/时,3小时后两车相遇。求乙车的速度。
甲车
乙车
255千米
42千米/时
?千米/时
甲行的路程
乙行的路程
甲路程+乙路程=总路程
解:设乙车的速度是X千米/时。
42×3+3x=255
速度和×时间=总路程
解:设乙车的速度是X千米/时。
3(42+X)=255
相遇问题
42×3
3x
快车和慢车同时从相距720千米的两地出发相向而行,4小时相遇。已知快车的速度是慢车的1.5倍,求快车的速度?
快车的路程+慢车的路程=总路程
解:设慢车的速度是X千米/时,则快车的速度是1.5X千米/时。。
4 1.5X+4X=720
6X+4X=720
10X=720
X=72
慢车的速度
1.5X=1.5×72=108
快车的速度
相遇问题
甲乙两个工程队合修一条长24千米的公路,甲队每天修0.32千米,比乙队每天少修0.11千米。两队从两端同时开工,几天后可以修好这条公路?
甲修的+乙修的=一共修的
解:设X天以后可以修好这条公路。
0.32X+(0.32+0.11)X=24
或(0.32+0.32+0.11)X=24
相遇问题
李老师带一笔钱去买文具. 如果买单价为8元的钢笔,正好用完;如果改买单价为6元的圆珠笔,则可以多买4支,钱也正好用完. 钢笔可以买多少支?李老师一共带了多少元?
解:设钢笔可以买x支,李老师一共带了8 x元. 下面方程正确的是( ).
A. 8 x = 6 x + 4 B. 8 x = 6( x + 4)
C. 8 x = 6 x - 4 D. 8 x = 6( x - 4)
B
选一选
作业:
练一练:列方程解应用题
1、小亚和小巧同时从相距960米的两地出发,相向而行,小亚平均每分钟走58米,小巧平均每分钟走62米,几分钟后两人在途中相遇?
2、两个城市之间的路程为405千米,一辆客车和一辆货车同时从这两个城市出发,相向而行,客车平均每小时行44千米,4.5小时后两车相遇,货车平均每小时行多少千米?
Thank you!
