3.2《列方程解决问题(四)》(第三时)教学课件(共25张PPT)五年级 数学下册 沪教版
文档属性
| 名称 | 3.2《列方程解决问题(四)》(第三时)教学课件(共25张PPT)五年级 数学下册 沪教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
列方程解决问题(四)
小学数学·五年级(下)
沪教版·第三单元
第三课时
在理解题意的基础上,寻找到问题中的等量关系,正确列出方程并解答。
在探究问题解题思路的过程中,体会利用等量关系分析、解决问题的优越性,发展方程思想。
从生活中提取素材,培养学生获取生活中数学信息的能力,让学生体验数学就在身边。
重
培养学生独立思考、解决问题的习惯和能力。
审题分析,找到相同的等量关系。
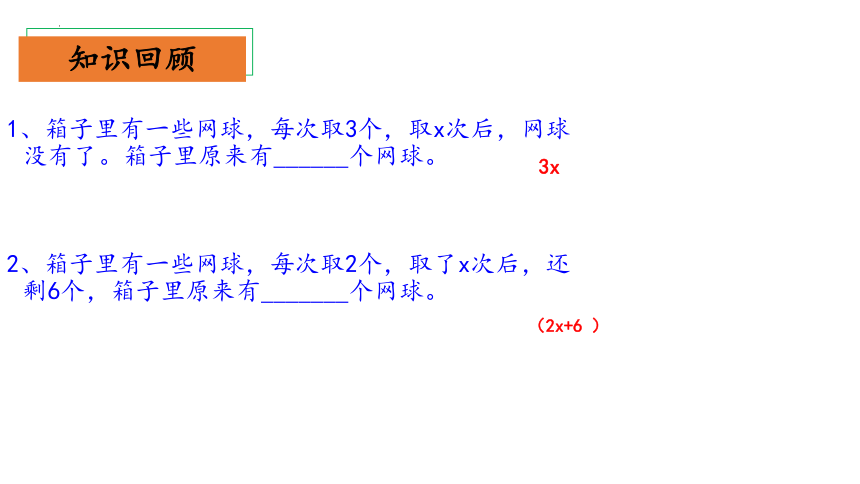
1、箱子里有一些网球,每次取3个,取x次后,网球没有了。箱子里原来有______个网球。
2、箱子里有一些网球,每次取2个,取了x次后,还剩6个,箱子里原来有_______个网球。
(2x+6 )
3x
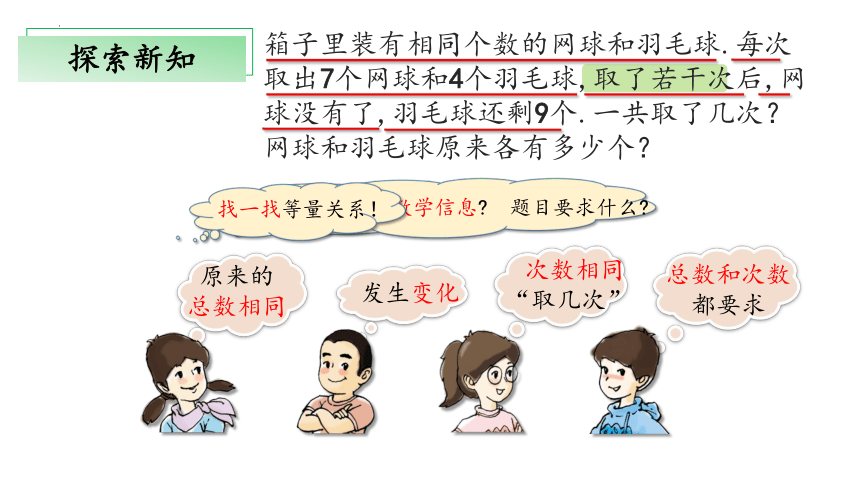
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
设一共取了X次,那么取出的网球个数可以用7X表示,取出的羽毛球个数可以用4X表示。
网球原来的个数=羽毛球原来的个数
分析
你了解到了哪些数学信息 题目要求什么
找一找等量关系!
总数和次数
都要求
次数相同
“取几次”
发生变化
原来的
总数相同
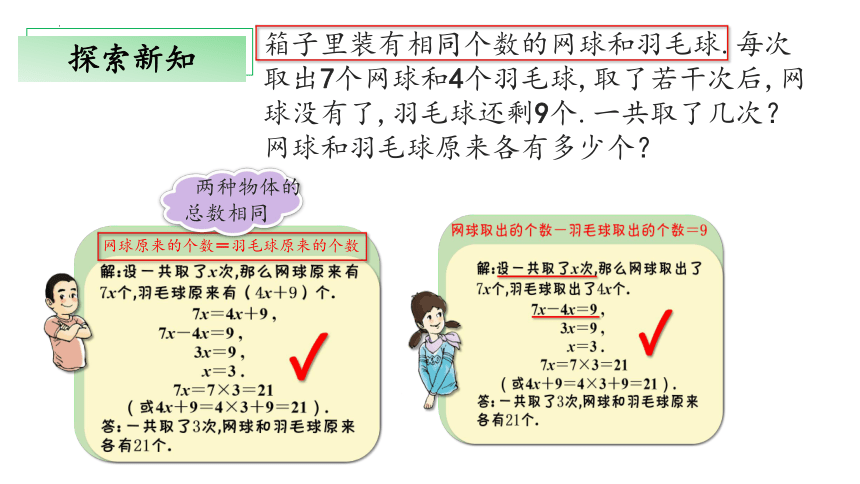
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
解:设一共取了x次,那么网球原来有7X个,羽毛球原来有(4X+9)个。
7X=4X+9
3X=9
X=3
7X=7×3=21
答:一共取了3次,网球和羽毛球原来各有21个。
检验:把答案代入原题算一算
7×3=21(个)
4×3+9=21(个)
或4X+9=4×3+9=21
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
我是这样想的:
由条件可知,取出的网球总数比羽毛球多9个,而每次取出的网球比羽毛球多(7-4)个。
所以,取球的次数是:
9÷(7-4)=3(次)
原来的网球数、羽毛球数量是:
3×7=21(个)或 4×3+9=21(个)
9÷(7-4)
=9÷3
=3(次)
3×7=21(个)
答:一共取了3次,网球和羽毛球原来各有21个。
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
网球原来的个数=羽毛球原来的个数
两种物体的
总数相同
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
试着用算术法来解答!
9÷(7-4)
=9÷3
=3(次).
7×3=21(个).
答:一共取了3次,网球和羽毛球原来各有21个.
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
方程法的思
路比较简单
方程法
算术法
9÷(7-4)
=9÷3
=3(次).
7×3=21(个).
答:一共取了3次,网球和羽毛球原来各有21个.
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
一盒糖果平均分给几个小朋友,如果每人分6颗,那么还剩下14颗;如果每人分8颗,那么正好分完,一共有几个小朋友 这盒糖果有多少颗
第一次分的糖果=第二次分的糖果
解:设一共有x个小朋友,那么这盒糖果有8x颗.
6x+14=8x
2x=14
x=7
8x=8×7=56 (或6x+14=6×7+14=56)
答:一共有7个小朋友,这盒糖果有56颗。
检验:把答案代入原题算一算
6×7+14=56(颗)
8×7=56(颗)
一盒糖果平均分给几个小朋友,如果每人分6颗,那么还剩下14颗;如果每人分8颗,那么正好分完,一共有几个小朋友 这盒糖果有多少颗
14÷(8-6)
=14÷2
=7(个)
8×7=56(颗)
答:一共有7个小朋友,这盒糖果有56颗。
或6×7+14
=42+14
=56(颗)
2. 盒子里的红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩6个,一共取了几次?白球和红球原来各有多少个?
解:设一共取了x次,那么红球原来有5X个,白球有(3x+6)个
5x=3x+6
5x-3x=6
x=3
红球:5x=5×3=15 白球:3x+6=3×3+6=15
答:一共取了3次,红球白球各有15个。
比较这两题的解答, 你有什么新的发现?虽然第一题讲的是一种物品两种不同的分法,第二题讲的是两种不同物品的不同的取法,但它们的共同点就是以相等的总数作为等量关系,因此列出方程的形式也是一样的。无论题目千变万化,只要等量关系不变,方程就不会改变。
箱子里有一些网球,每次取3个,取若干次后,网球没有了;如果每次取2个,取了相同次数后还剩6个,一共取了几次?
取法1的网球总数=取法2的网球总数
解:设一共取了x次。
3x=2x+6
3x-2x=6
x=6
答:一共取了6次。
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
网球的总数=羽毛球的总数
解:设一共取了x次,网球原来有7x个,羽毛球原来有(4x+9)个。
7x=4x+9
7x-4x = 9
x=3
网球7x=7×3=21羽毛球4x+9=21
答:一共取了3次,网球和羽毛球原来各有21个。
盒子里的红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩6个,一共取了几次?白球和红球原来各有多少个?
解:设一共取了x次,那么白球原来有5x个,红球原来有(3x+6)个。
5x=3x+6
一盒饼干平均分给几个小朋友,如果每人分6块。那么还剩下14块;如果每人分8块,那么还少了2块。一共有几个小朋友?这盒饼干有多少块?
解:设一共有x个小朋友,那么这盒饼干有(8x-2)块。
6x+14=8x-2
解:设一共有x个小朋友,那么这盒饼干有(6x+14)块。
1、一组学生栽树苗,如果每人栽6棵,还剩10棵;如果每人栽8棵,正好栽完。这组学生有多少人?
解:设这组学生有x人。
①、6( x+10 )=8x
②、6x+10=8x
一所学校给住宿学生分配宿舍。如果每间宿舍住6人,那么正好住满;如果每间宿舍住4人,那么正好缺12间宿舍。学生宿舍有多少间?
解:设学生宿舍有x间。
①、6x=4(x+12)
②、6x=4x+12
五(2)班男生人数与女生人数一样多。每组4名男生和5名女生,分了若干组后,男生还剩6人,女生还剩2人。一共分了几组( )
A. 4x+6=5x B. 4x+6=5x+2 C. 4x+6=5x-2
B
作业:
小丁丁和小胖要从甲乙两地出发相向而行。小丁丁的速度是75米/分,小胖的速度是60米/分,小胖先走45米后小丁丁才出发,结果他们正好在两地的中点处相遇。甲乙两地相距( )米。
看了这一题,你觉得这是一道怎样的应用题?为什么?动笔做一做。
Thank you!
列方程解决问题(四)
小学数学·五年级(下)
沪教版·第三单元
第三课时
在理解题意的基础上,寻找到问题中的等量关系,正确列出方程并解答。
在探究问题解题思路的过程中,体会利用等量关系分析、解决问题的优越性,发展方程思想。
从生活中提取素材,培养学生获取生活中数学信息的能力,让学生体验数学就在身边。
重
培养学生独立思考、解决问题的习惯和能力。
审题分析,找到相同的等量关系。
1、箱子里有一些网球,每次取3个,取x次后,网球没有了。箱子里原来有______个网球。
2、箱子里有一些网球,每次取2个,取了x次后,还剩6个,箱子里原来有_______个网球。
(2x+6 )
3x
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
设一共取了X次,那么取出的网球个数可以用7X表示,取出的羽毛球个数可以用4X表示。
网球原来的个数=羽毛球原来的个数
分析
你了解到了哪些数学信息 题目要求什么
找一找等量关系!
总数和次数
都要求
次数相同
“取几次”
发生变化
原来的
总数相同
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
解:设一共取了x次,那么网球原来有7X个,羽毛球原来有(4X+9)个。
7X=4X+9
3X=9
X=3
7X=7×3=21
答:一共取了3次,网球和羽毛球原来各有21个。
检验:把答案代入原题算一算
7×3=21(个)
4×3+9=21(个)
或4X+9=4×3+9=21
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
我是这样想的:
由条件可知,取出的网球总数比羽毛球多9个,而每次取出的网球比羽毛球多(7-4)个。
所以,取球的次数是:
9÷(7-4)=3(次)
原来的网球数、羽毛球数量是:
3×7=21(个)或 4×3+9=21(个)
9÷(7-4)
=9÷3
=3(次)
3×7=21(个)
答:一共取了3次,网球和羽毛球原来各有21个。
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
网球原来的个数=羽毛球原来的个数
两种物体的
总数相同
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
试着用算术法来解答!
9÷(7-4)
=9÷3
=3(次).
7×3=21(个).
答:一共取了3次,网球和羽毛球原来各有21个.
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
方程法的思
路比较简单
方程法
算术法
9÷(7-4)
=9÷3
=3(次).
7×3=21(个).
答:一共取了3次,网球和羽毛球原来各有21个.
箱子里装有相同个数的网球和羽毛球.每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个.一共取了几次?网球和羽毛球原来各有多少个?
一盒糖果平均分给几个小朋友,如果每人分6颗,那么还剩下14颗;如果每人分8颗,那么正好分完,一共有几个小朋友 这盒糖果有多少颗
第一次分的糖果=第二次分的糖果
解:设一共有x个小朋友,那么这盒糖果有8x颗.
6x+14=8x
2x=14
x=7
8x=8×7=56 (或6x+14=6×7+14=56)
答:一共有7个小朋友,这盒糖果有56颗。
检验:把答案代入原题算一算
6×7+14=56(颗)
8×7=56(颗)
一盒糖果平均分给几个小朋友,如果每人分6颗,那么还剩下14颗;如果每人分8颗,那么正好分完,一共有几个小朋友 这盒糖果有多少颗
14÷(8-6)
=14÷2
=7(个)
8×7=56(颗)
答:一共有7个小朋友,这盒糖果有56颗。
或6×7+14
=42+14
=56(颗)
2. 盒子里的红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩6个,一共取了几次?白球和红球原来各有多少个?
解:设一共取了x次,那么红球原来有5X个,白球有(3x+6)个
5x=3x+6
5x-3x=6
x=3
红球:5x=5×3=15 白球:3x+6=3×3+6=15
答:一共取了3次,红球白球各有15个。
比较这两题的解答, 你有什么新的发现?虽然第一题讲的是一种物品两种不同的分法,第二题讲的是两种不同物品的不同的取法,但它们的共同点就是以相等的总数作为等量关系,因此列出方程的形式也是一样的。无论题目千变万化,只要等量关系不变,方程就不会改变。
箱子里有一些网球,每次取3个,取若干次后,网球没有了;如果每次取2个,取了相同次数后还剩6个,一共取了几次?
取法1的网球总数=取法2的网球总数
解:设一共取了x次。
3x=2x+6
3x-2x=6
x=6
答:一共取了6次。
箱子里装有相同个数的网球和羽毛球。每次取出7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩9个,一共取了几次?网球和羽毛球原来各有多少个?
网球的总数=羽毛球的总数
解:设一共取了x次,网球原来有7x个,羽毛球原来有(4x+9)个。
7x=4x+9
7x-4x = 9
x=3
网球7x=7×3=21羽毛球4x+9=21
答:一共取了3次,网球和羽毛球原来各有21个。
盒子里的红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩6个,一共取了几次?白球和红球原来各有多少个?
解:设一共取了x次,那么白球原来有5x个,红球原来有(3x+6)个。
5x=3x+6
一盒饼干平均分给几个小朋友,如果每人分6块。那么还剩下14块;如果每人分8块,那么还少了2块。一共有几个小朋友?这盒饼干有多少块?
解:设一共有x个小朋友,那么这盒饼干有(8x-2)块。
6x+14=8x-2
解:设一共有x个小朋友,那么这盒饼干有(6x+14)块。
1、一组学生栽树苗,如果每人栽6棵,还剩10棵;如果每人栽8棵,正好栽完。这组学生有多少人?
解:设这组学生有x人。
①、6( x+10 )=8x
②、6x+10=8x
一所学校给住宿学生分配宿舍。如果每间宿舍住6人,那么正好住满;如果每间宿舍住4人,那么正好缺12间宿舍。学生宿舍有多少间?
解:设学生宿舍有x间。
①、6x=4(x+12)
②、6x=4x+12
五(2)班男生人数与女生人数一样多。每组4名男生和5名女生,分了若干组后,男生还剩6人,女生还剩2人。一共分了几组( )
A. 4x+6=5x B. 4x+6=5x+2 C. 4x+6=5x-2
B
作业:
小丁丁和小胖要从甲乙两地出发相向而行。小丁丁的速度是75米/分,小胖的速度是60米/分,小胖先走45米后小丁丁才出发,结果他们正好在两地的中点处相遇。甲乙两地相距( )米。
看了这一题,你觉得这是一道怎样的应用题?为什么?动笔做一做。
Thank you!
