青岛版九年级数学上册第3章3.5三角形的内切圆同步训练题(含答案)
文档属性
| 名称 | 青岛版九年级数学上册第3章3.5三角形的内切圆同步训练题(含答案) | 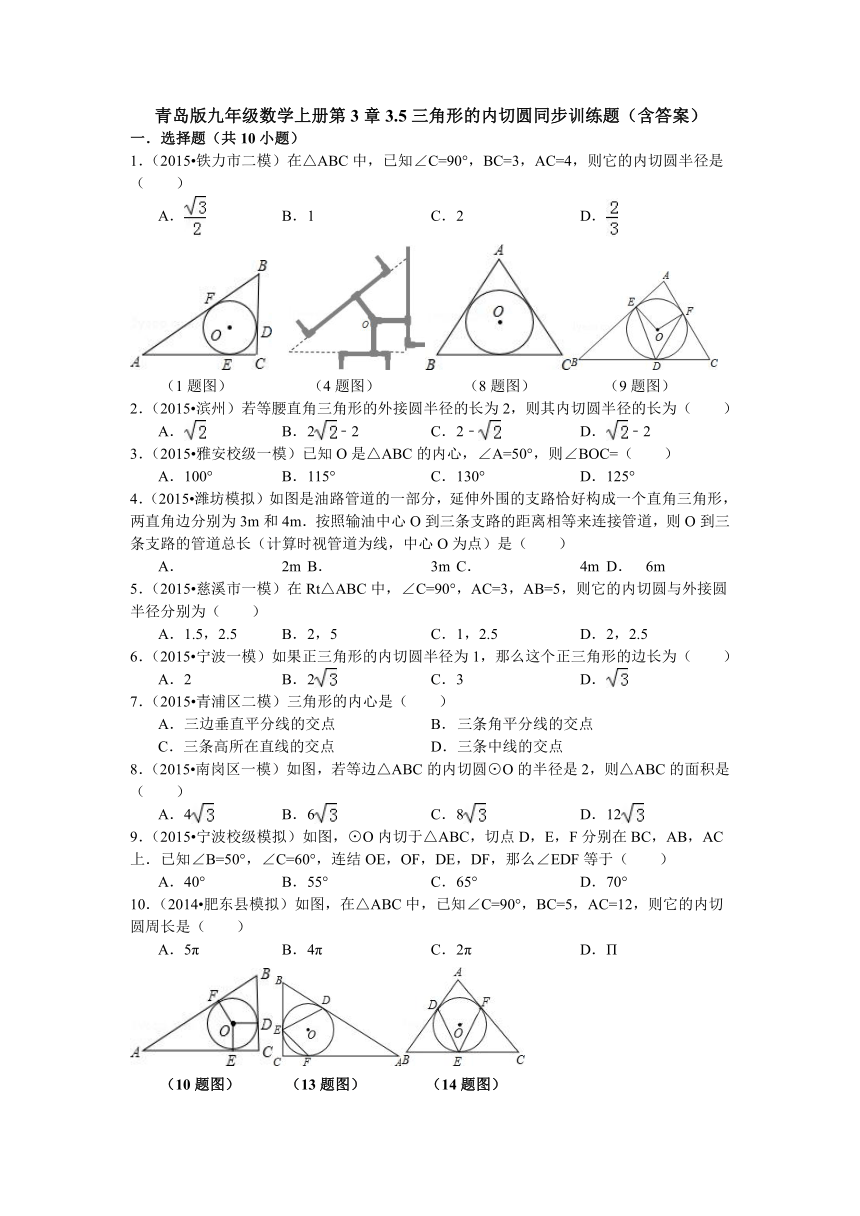 | |
| 格式 | zip | ||
| 文件大小 | 122.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-25 07:01:00 | ||
图片预览


文档简介
青岛版九年级数学上册第3章3.5三角形的内切圆同步训练题(含答案)
一.选择题(共10小题)
1.(2015 铁力市二模)在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A. B. 1 C. 2 D.
(1题图) (4题图) (8题图) (9题图)
2.(2015 滨州)若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A. B. 2﹣2 C. 2﹣ D. ﹣2
3.(2015 雅安校级一模)已知O是△ABC的内心,∠A=50°,则∠BOC=( )
A.100° B. 115° C. 130° D. 125°
4.(2015 潍坊模拟)如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3m和4m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A. 2m B. 3m C. 4m D. 6m
5.(2015 慈溪市一模)在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B. 2,5 C. 1,2.5 D. 2,2.5
6.(2015 宁波一模)如果正三角形的内切圆半径为1,那么这个正三角形的边长为( )
A.2 B. 2 C. 3 D.
7.(2015 青浦区二模)三角形的内心是( )
A.三边垂直平分线的交点 B. 三条角平分线的交点
C.三条高所在直线的交点 D. 三条中线的交点
8.(2015 南岗区一模)如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
A.4 B. 6 C. 8 D. 12
9.(2015 宁波校级模拟)如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
A.40° B. 55° C. 65° D. 70°
10.(2014 肥东县模拟)如图,在△ABC中,已知∠C=90°,BC=5,AC=12,则它的内切圆周长是( )
A.5π B. 4π C. 2π D. Π
(10题图) (13题图) (14题图)
二.填空题(共10小题)
11.(2015 大庆)边长为1的正三角形的内切圆半径为 .
12.(2015 雅安校级一模)在Rt△ABC中,∠C=90°,AB=5,BC=4,求内切圆半径 .
13.(2015 泰兴市校级一模)如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
14.(2015春 扶沟县期中)如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于 .
15.(2015春 雅安校级月考)O是△ABC的内心,∠A=70°,则∠BOC= .
16.(2014秋 冠县校级期末)在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
17.(2014秋 云梦县校级期末)已知在三角形中∠C=90°,AC=3,BC=4,则△ABC的内切圆的面积是 .
18.(2014秋 广东期末)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= .
(18题图) (19题图) (20题图)
19.(2014秋 海珠区期末)如图,⊙O是△ABC的内切圆,其切点分别为D、E、F,且BD=3,AE=2,则AB= .
20.(2014秋 沛县期末)如图,⊙O是△ABC的内切圆,若∠ABC=60°,∠ACB=40°,则∠BOC= °.
三.解答题(共5小题)
21.(2015 临沂模拟)在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
22.(2015 槐荫区二模)如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.
23.(2014 西安模拟)已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.
(1)求证:EB=EN=EC;
(2)求证:NE2=AE DE.
24.(2014秋 东莞期末)如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
25.(2014秋 安阳县期末)如图,线段AB、AC分别与⊙O相切于点E、F,连接BC,OC平分∠ACB.
(1)求证:BC与⊙O相切;
(2)如果AC=5,AB=4,BC=3,求⊙O的半径.
青岛版九年级数学上册第3章3.5三角形的内切圆同步训练题参考答案
一.选择题(共10小题)
1.B 2.B 3.B 4.B 5.C 6.B 7.B 8.D 9.B 10.B
二.填空题(共10小题)
11. 12.1 13.80 14.72° 15.125° 16.2:5 17.π
18.1 19.5 20.130
三.解答题(共5小题)
21.(1)证明:如图连结OE,OF,OG.
∵⊙O是△ABC的内切圆,∠C=90°,∴四边形CEOF是正方形,∴CE=CF=r.
又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5,∴(3﹣r)+(4﹣r)=5.解得r=1;
(2)解:连结OA,在Rt△AOG中,
∵r=1,AG=3﹣r=2,∴tan∠OAG==.
(21) (22)
22.解:连接OD、OF,
∵E、F均为切点,∴OD⊥AB,OF⊥AC,
∵∠B=66°,∠C=37°,∴∠A=180°﹣∠B﹣∠C=77°,
∴∠O=360°﹣∠A﹣∠ADO﹣∠AFO=103°,
∵弧DF=弧DF,∴∠M=∠O=51.5°.
23.证明:(1)连接BN,
∵点N为△ABC的内心,∴∠1=∠2,∠3=∠4.∴∠BCE=∠1,∴EB=EC.
∵∠5与∠2都是弧EC所对的圆周角,∴∠5=∠2=∠1.∴∠4+∠5=∠3+∠1.
∵∠NBE=∠4+∠5,∠BNE=∠3+∠1,∴∠NBE=∠BNE.∴EB=EN.∴EB=EN=EC.
(2)由(1)知∠5=∠2=∠1,∠BED=∠AEB,
∴△BED∽△AEB.∴.即BE2=AE DE.∵EB=EN,∴NE2=AE DE.
(23) (24) (25)
24.解法一:(1)证明:∵⊙O是△ABC的内切圆,切点为D、E、F
∴AD=AF,BD=BE,CE=CF,
∵AB=AC,∴AB﹣AD=AC﹣AF,即BD=CF,∴BE=CE;
解法二:(1)证明:连结OB、OC、OE
∵⊙O是△ABC的内切圆,∴OB,OC分别平分∠ABC,∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵AB=AC,∴∠ABC=∠ACB,∴∠OBC=∠OCB,∴OB=OC,
又∵⊙O是△ABC的内切圆,切点为E,
∴OE⊥BC,
∴BE=CE;
(2)解:连结OD、OE,∵⊙O是△ABC的内切圆,切点为D、E、F,
∴∠ODA=∠OFA=∠A=90°,
又∵OD=OF,∴四边形ODAF是正方形,
设OD=AD=AF=r,则BE=BD=CF=CE=2﹣r,
在△ABC中,∠A=90°,∴,
又∵BC=BE+CE,∴(2﹣r)+(2﹣r)=,得:r=,∴⊙O的半径是.
25.(1)证明:连接OF,过点O作ON⊥BC于点N,
∵AC与⊙O相切于点F,∴OF⊥AC,
∵OC平分∠ACB,ON⊥BC,∴OF=ON,∴BC与⊙O相切;
(2)解:∵AC=5,AB=4,BC=3,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴⊙O的半径为:=1.
一.选择题(共10小题)
1.(2015 铁力市二模)在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A. B. 1 C. 2 D.
(1题图) (4题图) (8题图) (9题图)
2.(2015 滨州)若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A. B. 2﹣2 C. 2﹣ D. ﹣2
3.(2015 雅安校级一模)已知O是△ABC的内心,∠A=50°,则∠BOC=( )
A.100° B. 115° C. 130° D. 125°
4.(2015 潍坊模拟)如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3m和4m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A. 2m B. 3m C. 4m D. 6m
5.(2015 慈溪市一模)在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B. 2,5 C. 1,2.5 D. 2,2.5
6.(2015 宁波一模)如果正三角形的内切圆半径为1,那么这个正三角形的边长为( )
A.2 B. 2 C. 3 D.
7.(2015 青浦区二模)三角形的内心是( )
A.三边垂直平分线的交点 B. 三条角平分线的交点
C.三条高所在直线的交点 D. 三条中线的交点
8.(2015 南岗区一模)如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
A.4 B. 6 C. 8 D. 12
9.(2015 宁波校级模拟)如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
A.40° B. 55° C. 65° D. 70°
10.(2014 肥东县模拟)如图,在△ABC中,已知∠C=90°,BC=5,AC=12,则它的内切圆周长是( )
A.5π B. 4π C. 2π D. Π
(10题图) (13题图) (14题图)
二.填空题(共10小题)
11.(2015 大庆)边长为1的正三角形的内切圆半径为 .
12.(2015 雅安校级一模)在Rt△ABC中,∠C=90°,AB=5,BC=4,求内切圆半径 .
13.(2015 泰兴市校级一模)如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
14.(2015春 扶沟县期中)如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于 .
15.(2015春 雅安校级月考)O是△ABC的内心,∠A=70°,则∠BOC= .
16.(2014秋 冠县校级期末)在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
17.(2014秋 云梦县校级期末)已知在三角形中∠C=90°,AC=3,BC=4,则△ABC的内切圆的面积是 .
18.(2014秋 广东期末)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= .
(18题图) (19题图) (20题图)
19.(2014秋 海珠区期末)如图,⊙O是△ABC的内切圆,其切点分别为D、E、F,且BD=3,AE=2,则AB= .
20.(2014秋 沛县期末)如图,⊙O是△ABC的内切圆,若∠ABC=60°,∠ACB=40°,则∠BOC= °.
三.解答题(共5小题)
21.(2015 临沂模拟)在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
22.(2015 槐荫区二模)如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.
23.(2014 西安模拟)已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.
(1)求证:EB=EN=EC;
(2)求证:NE2=AE DE.
24.(2014秋 东莞期末)如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
25.(2014秋 安阳县期末)如图,线段AB、AC分别与⊙O相切于点E、F,连接BC,OC平分∠ACB.
(1)求证:BC与⊙O相切;
(2)如果AC=5,AB=4,BC=3,求⊙O的半径.
青岛版九年级数学上册第3章3.5三角形的内切圆同步训练题参考答案
一.选择题(共10小题)
1.B 2.B 3.B 4.B 5.C 6.B 7.B 8.D 9.B 10.B
二.填空题(共10小题)
11. 12.1 13.80 14.72° 15.125° 16.2:5 17.π
18.1 19.5 20.130
三.解答题(共5小题)
21.(1)证明:如图连结OE,OF,OG.
∵⊙O是△ABC的内切圆,∠C=90°,∴四边形CEOF是正方形,∴CE=CF=r.
又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5,∴(3﹣r)+(4﹣r)=5.解得r=1;
(2)解:连结OA,在Rt△AOG中,
∵r=1,AG=3﹣r=2,∴tan∠OAG==.
(21) (22)
22.解:连接OD、OF,
∵E、F均为切点,∴OD⊥AB,OF⊥AC,
∵∠B=66°,∠C=37°,∴∠A=180°﹣∠B﹣∠C=77°,
∴∠O=360°﹣∠A﹣∠ADO﹣∠AFO=103°,
∵弧DF=弧DF,∴∠M=∠O=51.5°.
23.证明:(1)连接BN,
∵点N为△ABC的内心,∴∠1=∠2,∠3=∠4.∴∠BCE=∠1,∴EB=EC.
∵∠5与∠2都是弧EC所对的圆周角,∴∠5=∠2=∠1.∴∠4+∠5=∠3+∠1.
∵∠NBE=∠4+∠5,∠BNE=∠3+∠1,∴∠NBE=∠BNE.∴EB=EN.∴EB=EN=EC.
(2)由(1)知∠5=∠2=∠1,∠BED=∠AEB,
∴△BED∽△AEB.∴.即BE2=AE DE.∵EB=EN,∴NE2=AE DE.
(23) (24) (25)
24.解法一:(1)证明:∵⊙O是△ABC的内切圆,切点为D、E、F
∴AD=AF,BD=BE,CE=CF,
∵AB=AC,∴AB﹣AD=AC﹣AF,即BD=CF,∴BE=CE;
解法二:(1)证明:连结OB、OC、OE
∵⊙O是△ABC的内切圆,∴OB,OC分别平分∠ABC,∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵AB=AC,∴∠ABC=∠ACB,∴∠OBC=∠OCB,∴OB=OC,
又∵⊙O是△ABC的内切圆,切点为E,
∴OE⊥BC,
∴BE=CE;
(2)解:连结OD、OE,∵⊙O是△ABC的内切圆,切点为D、E、F,
∴∠ODA=∠OFA=∠A=90°,
又∵OD=OF,∴四边形ODAF是正方形,
设OD=AD=AF=r,则BE=BD=CF=CE=2﹣r,
在△ABC中,∠A=90°,∴,
又∵BC=BE+CE,∴(2﹣r)+(2﹣r)=,得:r=,∴⊙O的半径是.
25.(1)证明:连接OF,过点O作ON⊥BC于点N,
∵AC与⊙O相切于点F,∴OF⊥AC,
∵OC平分∠ACB,ON⊥BC,∴OF=ON,∴BC与⊙O相切;
(2)解:∵AC=5,AB=4,BC=3,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴⊙O的半径为:=1.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
