17.2.2 勾股定理的逆定理的应用(第二课时)课件(共30张PPT)【2024春人教八下数学同步优质课件】
文档属性
| 名称 | 17.2.2 勾股定理的逆定理的应用(第二课时)课件(共30张PPT)【2024春人教八下数学同步优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览








文档简介
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
17.2 勾股定理逆的定理
17.2.2 勾股定理逆的定理的应用
第十七章 勾股定理
1.灵活应用勾股定理及其逆定理解决实际问题.(重点)
2.将实际问题转化成用勾股定理的逆定理解决的数学问题.(难点)
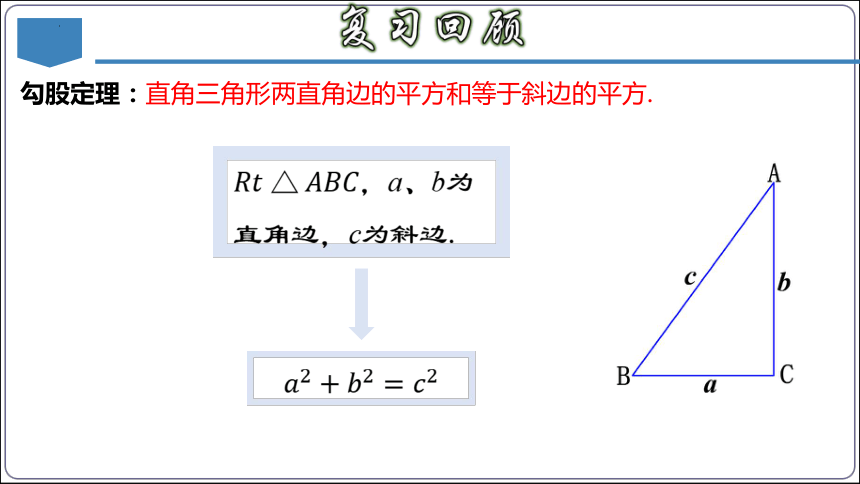
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
????????△????????????,a、b为直角边,c为斜边.
?
????2+????2=????2
?
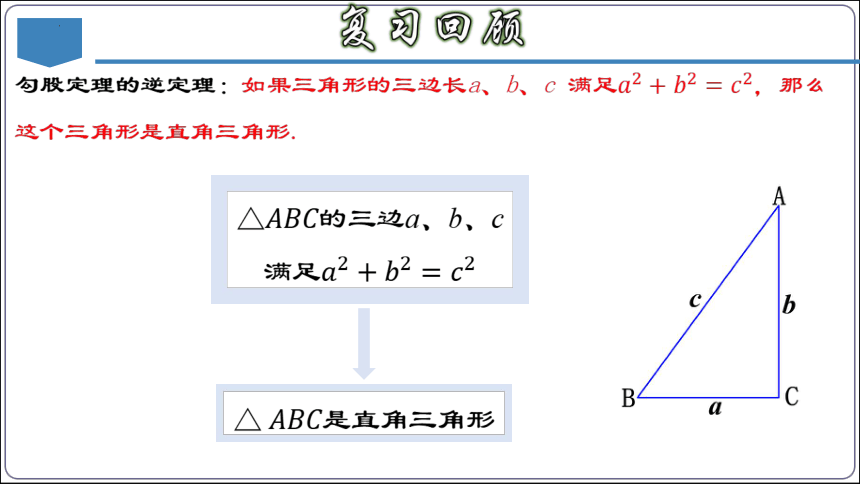
勾股定理的逆定理:如果三角形的三边长a、b、c 满足????2+????2=????2,那么这个三角形是直角三角形.
?
△????????????的三边a、b、c满足????2+????2=????2
?
△????????????是直角三角形
?
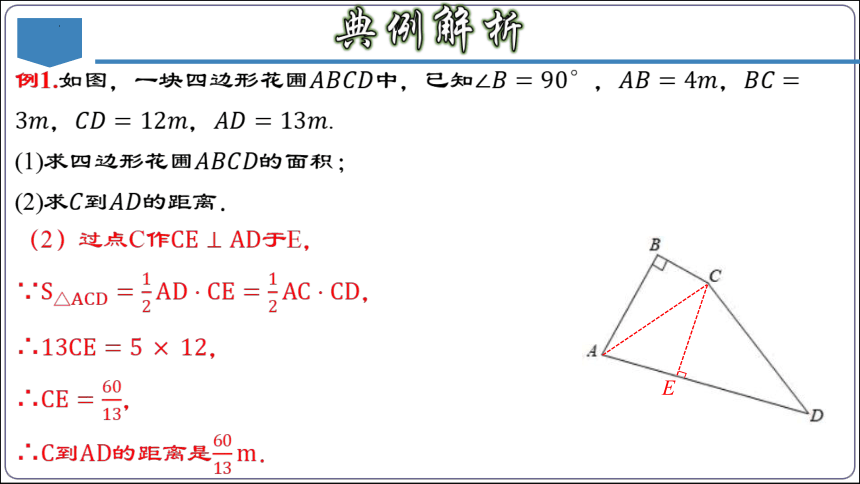
例1.如图,一块四边形花圃????????????????中,已知∠????=90°,????????=4????,????????=3????,????????=12????,????????=13????.
(1)求四边形花圃????????????????的面积;
(2)求????到????????的距离.
?
(1)解:连接????????,
∵∠????=90°,????????=4????,????????=3????,
∴????????=????????2+????????2=42+32=5m,
∵????????=12????,????????=13????,
∴????????2+????????2=52+122=132=????????2,
∴△????????????是直角三角形,且∠????????????=90°,
?
例1.如图,一块四边形花圃????????????????中,已知∠????=90°,????????=4????,????????=3????,????????=12????,????????=13????.
(1)求四边形花圃????????????????的面积;
(2)求????到????????的距离.
?
∴四边形花圃????????????????的面积=????△????????????+????△????????????
=12?????????????????+12?????????????????
=12×4×3+12×5×12
=36
∴四边形花圃????????????????的面积是36m2;
?
例1.如图,一块四边形花圃????????????????中,已知∠????=90°,????????=4????,????????=3????,????????=12????,????????=13????.
(1)求四边形花圃????????????????的面积;
(2)求????到????????的距离.
?
(2)过点C作CE⊥AD于E,
∵S△ACD=12AD?CE=12AC?CD,
∴13CE=5×12,
∴CE=6013,
∴C到AD的距离是6013m.
?
E
例2.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中????????=????????,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路????????,测得????????=13千米,????????=12千米,????????=5千米.求原来的路线????????的长.
?
解:∵????????=13千米,????????=12千米,????????=5千米,即52+122=132,
∴????????2=????????2+????????2,
∴△????????????是直角三角形,且∠????????????=90°,
∴∠????????????=90°,
∴????????2=????????2+????????2,
?
例2.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中????????=????????,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路????????,测得????????=13千米,????????=12千米,????????=5千米.求原来的路线????????的长.
?
设????????=????????=????,
∴????????=?????????????????=?????5,
∴????2=?????52+122,即10????=169,
解得:????=16.9,
答:原来的路线????????的长为16.9千米.
?
2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知????????=9????,????????=12????,????????=17????,????????=8????,技术人员通过测量确定了∠????????????=90°.
(1)问这片绿地的面积是多少?
(2)小区内部分居民每天必须从点????经过点????再到点????
位置,为了方便居民出入,技术人员打算在绿地中
开辟一条从点????直通点????的小路,请问如果方案落实
施工完成,居民从点????到点????将少走多少路程?
?
(1)解:如图,连接????????,
∵∠????????????=90°,????????=9????,????????=12????,
∴????????=????????2+????????2=92+122=15????,
∵????????=17????,????????=8????,
∴????????2+????????2=????????2,
∴△????????????是直角三角形,即∠????????????=90°,
∴????△????????????=12?????????????????=12×8×15=60????2,????△????????????=12?????????????????=12×9×12=54????2,
∴????四边形????????????????=????△????????????+????△????????????=60+54=114????2,
?
(2)解:????????+?????????????????=9+12?15=6????,
?
2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知??
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
∵ 242+182=302,即PQ2+PR2=QR2
∴ ∠QPR=90°
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.
例3.如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【点睛】解决实际问题的步骤:?构建几何模型(从整体到局部);?标注有用信息,明确已知和所求;?应用数学知识求解.
如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
分析:根据勾股定理的逆定理得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三角形面积公式有
12BC·AB=12AC·BD,
即6×8=10BD,解得BD=245.
在Rt△BCD中,
?
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
例4.如图,已知等腰△ABC的底边BC=210cm,AH平分∠BAC交BC于H,D是腰AC上点,且CD=2cm,BD=6cm,求AH的长.
?
解:∵BC=210,BD=6,CD=2,
∴????????2=(210)2=40,????????2+????????2=62+22=40,
∴????????2=????????2+????????2,
∴△BDC为直角三角形,
∴∠BDC=∠ADB=90°,
∵△ABC是等腰三角形,
∴AB=AC,
设AD=x,则AB=AC=x+2,
?
例4.如图,已知等腰△ABC的底边BC=210cm,AH平分∠BAC交BC于H,D是腰AC上点,且CD=2cm,BD=6cm,求AH的长.
?
在Rt△ABD中,勾股定理得????2+62=(????+2)2,
解得x=8,
∴AB=8+2=10,
∵AB=AC,AH⊥BC,BC=210,
∴BH=HC=10,
由勾股定理得AH=????????2?????????2=310 (cm).
?
例5.如图所示,在△????????????中,????????:????????:????????=3:4:5,且△????????????的周长为36????????,点P从点A开始沿????????边向B点以每秒1????????的速度移动;点Q从点B沿????????边向点C以每秒2????????的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
?
解:设????????为3????????????,????????为4????????????,????????为5????????????,
∵△????????????的周长为36????????,
∴????????+????????+????????=36????????,
即3????+4????+5????=36,
解得:????=3,
∴????????=9????????,????????=12????????,????????=15????????,
∵????????2+????????2=????????2
?
例5.如图所示,在△????????????中,????????:????????:????????=3:4:5,且△????????????的周长为36????????,点P从点A开始沿????????边向B点以每秒1????????的速度移动;点Q从点B沿????????边向点C以每秒2????????的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
?
∴△????????????是直角三角形,且∠????=90°.
经过3秒时,????????=9?3×1=6????????,????????=2×3=6????????,
又∵在Rt△????????????中,????????2=????????2+????????2,
∴????????=62????????,
即经过3秒时,P、Q两点间的距离为62????????.
?
1.在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是(?? ??)
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
C
2.如图,在Rt△ABC中,AB=8,AC=6,BC=10,D是AB的中点,P,Q分别是BC,DC上的动点,则AQ+QP的最小值是________.
4.8
3.已知:如图,四边形ABCD中,AB=20,BC=15, CD=7,AD=24,∠B=90°.求证:∠A+∠C=180.
证明:连接AC.
在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=202+152=252
∴AC=25
∵72+242=252
即CD2+AD2=AC2
∴∠D=90°
∴∠DAB+∠BCD=360°-∠B-∠D=180°
4.如图,有一块地,已知∠ADC=90°,AD=4m, CD=3m,AB=13m,BC=12m.求这块地的面积.
解:连接AC.
在Rt△ACD中,根据勾股定理,
AC2=AD2+CD2=42+32=25
∴AC=5m
∵52+122=132
即AC2+BC2=AB2
∴∠ACB=90°
∴S阴=S△ABC-S△ACD=12×5×12-12×3×4=24(m2)
?
5.如图,A,B,C,D是四个小镇,它们之间除(B,C外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A ? B:10元; A ? C:12. 5元; A ? D:8元; B ? D: 6元;C ? D:4.5元.为了B,C之间的交通方便,在B,C之间建成笔直的公路,请按上述标准计算出B,C之间的公路的票价为多少元?
解:连接BC.
∵82+62=102,即AD2+BD2=AB2
∴∠ADB=90°,∴∠BDC=90
在Rt△BDC中,根据勾股定理,BC=????????2+????????2= 62+4.52?=7.5
因此,B,C之间的公路的票价为7.5元.
?
6.某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离????????=30????????,????????=40????????,????????=50????????,以沙尘暴中心为圆心,周围25????????以内都会受到沙尘暴影响.
(1)通过计算说明城镇C是否会受到影响;
?
(1)解:作????????⊥????????于D,
在三角形????????????中,????????2+????????2=302+402=????????2,
∴△????????????是直角三角形,即∠????????????=90°,
12?????????????????=12?????????????????,
12×50?????????=12×30×40,
解得∶????????=24km<25千米,
所以,城镇C会受到影响.
?
D
6.某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离????????=30????????,????????=40????????,????????=50????????,以沙尘暴中心为圆心,周围25????????以内都会受到沙尘暴影响.
(2)若沙尘暴中心的移动速度为20????????/h,则沙尘暴影响该城镇持续的时间有多长?
?
(2)解:设沙尘暴中心到点E处城镇C开始受到影响,此时CE=25千米,
到F处结束影响,此时CF=25千米,
DE=CE2?CD2=252?242=7,
EF=2DE=14千米,
受影响的时间为14÷20=0.7(小时)
?
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
17.2 勾股定理逆的定理
17.2.2 勾股定理逆的定理的应用
第十七章 勾股定理
1.灵活应用勾股定理及其逆定理解决实际问题.(重点)
2.将实际问题转化成用勾股定理的逆定理解决的数学问题.(难点)
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
????????△????????????,a、b为直角边,c为斜边.
?
????2+????2=????2
?
勾股定理的逆定理:如果三角形的三边长a、b、c 满足????2+????2=????2,那么这个三角形是直角三角形.
?
△????????????的三边a、b、c满足????2+????2=????2
?
△????????????是直角三角形
?
例1.如图,一块四边形花圃????????????????中,已知∠????=90°,????????=4????,????????=3????,????????=12????,????????=13????.
(1)求四边形花圃????????????????的面积;
(2)求????到????????的距离.
?
(1)解:连接????????,
∵∠????=90°,????????=4????,????????=3????,
∴????????=????????2+????????2=42+32=5m,
∵????????=12????,????????=13????,
∴????????2+????????2=52+122=132=????????2,
∴△????????????是直角三角形,且∠????????????=90°,
?
例1.如图,一块四边形花圃????????????????中,已知∠????=90°,????????=4????,????????=3????,????????=12????,????????=13????.
(1)求四边形花圃????????????????的面积;
(2)求????到????????的距离.
?
∴四边形花圃????????????????的面积=????△????????????+????△????????????
=12?????????????????+12?????????????????
=12×4×3+12×5×12
=36
∴四边形花圃????????????????的面积是36m2;
?
例1.如图,一块四边形花圃????????????????中,已知∠????=90°,????????=4????,????????=3????,????????=12????,????????=13????.
(1)求四边形花圃????????????????的面积;
(2)求????到????????的距离.
?
(2)过点C作CE⊥AD于E,
∵S△ACD=12AD?CE=12AC?CD,
∴13CE=5×12,
∴CE=6013,
∴C到AD的距离是6013m.
?
E
例2.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中????????=????????,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路????????,测得????????=13千米,????????=12千米,????????=5千米.求原来的路线????????的长.
?
解:∵????????=13千米,????????=12千米,????????=5千米,即52+122=132,
∴????????2=????????2+????????2,
∴△????????????是直角三角形,且∠????????????=90°,
∴∠????????????=90°,
∴????????2=????????2+????????2,
?
例2.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中????????=????????,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路????????,测得????????=13千米,????????=12千米,????????=5千米.求原来的路线????????的长.
?
设????????=????????=????,
∴????????=?????????????????=?????5,
∴????2=?????52+122,即10????=169,
解得:????=16.9,
答:原来的路线????????的长为16.9千米.
?
2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知????????=9????,????????=12????,????????=17????,????????=8????,技术人员通过测量确定了∠????????????=90°.
(1)问这片绿地的面积是多少?
(2)小区内部分居民每天必须从点????经过点????再到点????
位置,为了方便居民出入,技术人员打算在绿地中
开辟一条从点????直通点????的小路,请问如果方案落实
施工完成,居民从点????到点????将少走多少路程?
?
(1)解:如图,连接????????,
∵∠????????????=90°,????????=9????,????????=12????,
∴????????=????????2+????????2=92+122=15????,
∵????????=17????,????????=8????,
∴????????2+????????2=????????2,
∴△????????????是直角三角形,即∠????????????=90°,
∴????△????????????=12?????????????????=12×8×15=60????2,????△????????????=12?????????????????=12×9×12=54????2,
∴????四边形????????????????=????△????????????+????△????????????=60+54=114????2,
?
(2)解:????????+?????????????????=9+12?15=6????,
?
2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知??
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
∵ 242+182=302,即PQ2+PR2=QR2
∴ ∠QPR=90°
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.
例3.如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【点睛】解决实际问题的步骤:?构建几何模型(从整体到局部);?标注有用信息,明确已知和所求;?应用数学知识求解.
如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
分析:根据勾股定理的逆定理得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三角形面积公式有
12BC·AB=12AC·BD,
即6×8=10BD,解得BD=245.
在Rt△BCD中,
?
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
例4.如图,已知等腰△ABC的底边BC=210cm,AH平分∠BAC交BC于H,D是腰AC上点,且CD=2cm,BD=6cm,求AH的长.
?
解:∵BC=210,BD=6,CD=2,
∴????????2=(210)2=40,????????2+????????2=62+22=40,
∴????????2=????????2+????????2,
∴△BDC为直角三角形,
∴∠BDC=∠ADB=90°,
∵△ABC是等腰三角形,
∴AB=AC,
设AD=x,则AB=AC=x+2,
?
例4.如图,已知等腰△ABC的底边BC=210cm,AH平分∠BAC交BC于H,D是腰AC上点,且CD=2cm,BD=6cm,求AH的长.
?
在Rt△ABD中,勾股定理得????2+62=(????+2)2,
解得x=8,
∴AB=8+2=10,
∵AB=AC,AH⊥BC,BC=210,
∴BH=HC=10,
由勾股定理得AH=????????2?????????2=310 (cm).
?
例5.如图所示,在△????????????中,????????:????????:????????=3:4:5,且△????????????的周长为36????????,点P从点A开始沿????????边向B点以每秒1????????的速度移动;点Q从点B沿????????边向点C以每秒2????????的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
?
解:设????????为3????????????,????????为4????????????,????????为5????????????,
∵△????????????的周长为36????????,
∴????????+????????+????????=36????????,
即3????+4????+5????=36,
解得:????=3,
∴????????=9????????,????????=12????????,????????=15????????,
∵????????2+????????2=????????2
?
例5.如图所示,在△????????????中,????????:????????:????????=3:4:5,且△????????????的周长为36????????,点P从点A开始沿????????边向B点以每秒1????????的速度移动;点Q从点B沿????????边向点C以每秒2????????的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
?
∴△????????????是直角三角形,且∠????=90°.
经过3秒时,????????=9?3×1=6????????,????????=2×3=6????????,
又∵在Rt△????????????中,????????2=????????2+????????2,
∴????????=62????????,
即经过3秒时,P、Q两点间的距离为62????????.
?
1.在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是(?? ??)
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
C
2.如图,在Rt△ABC中,AB=8,AC=6,BC=10,D是AB的中点,P,Q分别是BC,DC上的动点,则AQ+QP的最小值是________.
4.8
3.已知:如图,四边形ABCD中,AB=20,BC=15, CD=7,AD=24,∠B=90°.求证:∠A+∠C=180.
证明:连接AC.
在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=202+152=252
∴AC=25
∵72+242=252
即CD2+AD2=AC2
∴∠D=90°
∴∠DAB+∠BCD=360°-∠B-∠D=180°
4.如图,有一块地,已知∠ADC=90°,AD=4m, CD=3m,AB=13m,BC=12m.求这块地的面积.
解:连接AC.
在Rt△ACD中,根据勾股定理,
AC2=AD2+CD2=42+32=25
∴AC=5m
∵52+122=132
即AC2+BC2=AB2
∴∠ACB=90°
∴S阴=S△ABC-S△ACD=12×5×12-12×3×4=24(m2)
?
5.如图,A,B,C,D是四个小镇,它们之间除(B,C外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A ? B:10元; A ? C:12. 5元; A ? D:8元; B ? D: 6元;C ? D:4.5元.为了B,C之间的交通方便,在B,C之间建成笔直的公路,请按上述标准计算出B,C之间的公路的票价为多少元?
解:连接BC.
∵82+62=102,即AD2+BD2=AB2
∴∠ADB=90°,∴∠BDC=90
在Rt△BDC中,根据勾股定理,BC=????????2+????????2= 62+4.52?=7.5
因此,B,C之间的公路的票价为7.5元.
?
6.某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离????????=30????????,????????=40????????,????????=50????????,以沙尘暴中心为圆心,周围25????????以内都会受到沙尘暴影响.
(1)通过计算说明城镇C是否会受到影响;
?
(1)解:作????????⊥????????于D,
在三角形????????????中,????????2+????????2=302+402=????????2,
∴△????????????是直角三角形,即∠????????????=90°,
12?????????????????=12?????????????????,
12×50?????????=12×30×40,
解得∶????????=24km<25千米,
所以,城镇C会受到影响.
?
D
6.某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离????????=30????????,????????=40????????,????????=50????????,以沙尘暴中心为圆心,周围25????????以内都会受到沙尘暴影响.
(2)若沙尘暴中心的移动速度为20????????/h,则沙尘暴影响该城镇持续的时间有多长?
?
(2)解:设沙尘暴中心到点E处城镇C开始受到影响,此时CE=25千米,
到F处结束影响,此时CF=25千米,
DE=CE2?CD2=252?242=7,
EF=2DE=14千米,
受影响的时间为14÷20=0.7(小时)
?
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
