17.3 第十七章 勾股定理 章节复习 课件(共62张PPT)【2024春人教八下数学同步优质课件】
文档属性
| 名称 | 17.3 第十七章 勾股定理 章节复习 课件(共62张PPT)【2024春人教八下数学同步优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 20:23:51 | ||
图片预览







文档简介
(共62张PPT)
人教八下数学
同步优质课件
人教版八年级下册
知识网络
学习目标
知识梳理
迁移应用
2024春人教版八(下)数学同步精品课件
考点解析
考点梳理
章节复习
第十七章 勾股定理
1.复习与回顾本章的重要知识点; (重点)
2.勾股定理及其逆定理的用途和相互关系;
3.总结本章的重要思想方法及其应用;(难点)
4.勾股定理及逆定理的综合运用.(难点)
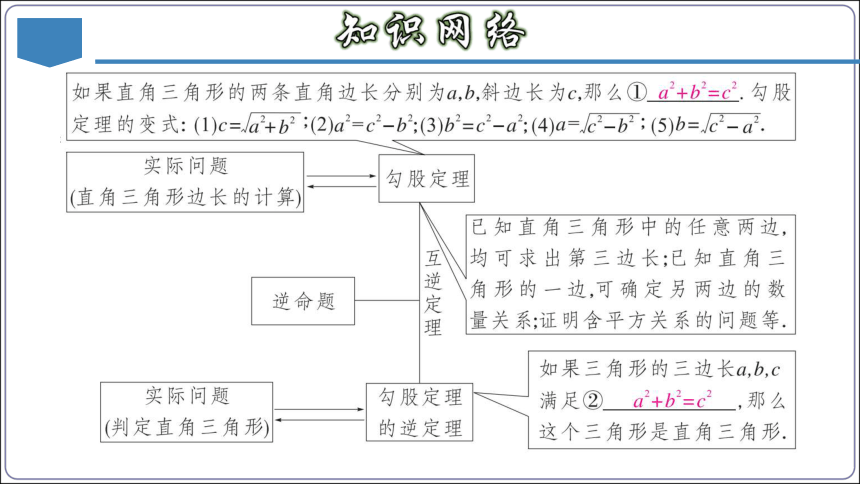
一、勾股定理
勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
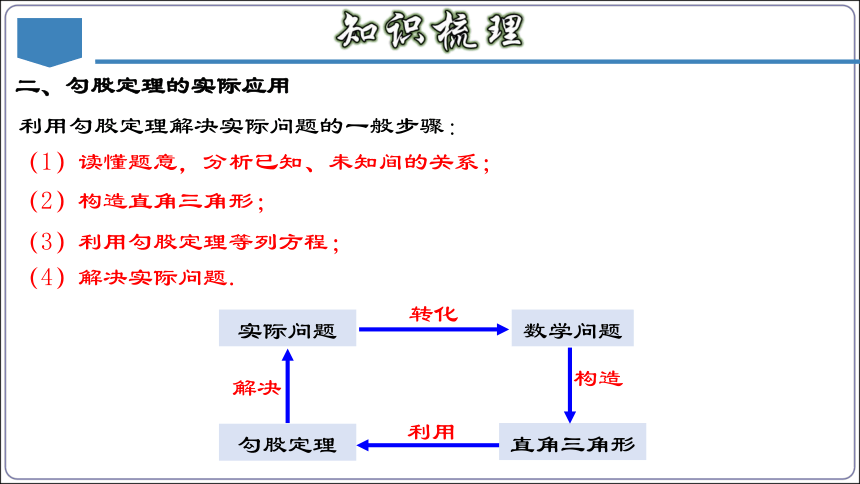
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
利用
构造
解决
二、勾股定理的实际应用
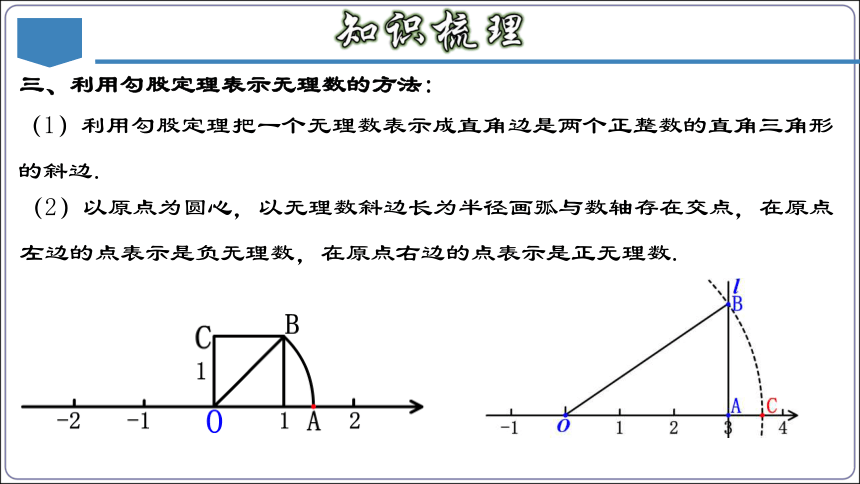
三、利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
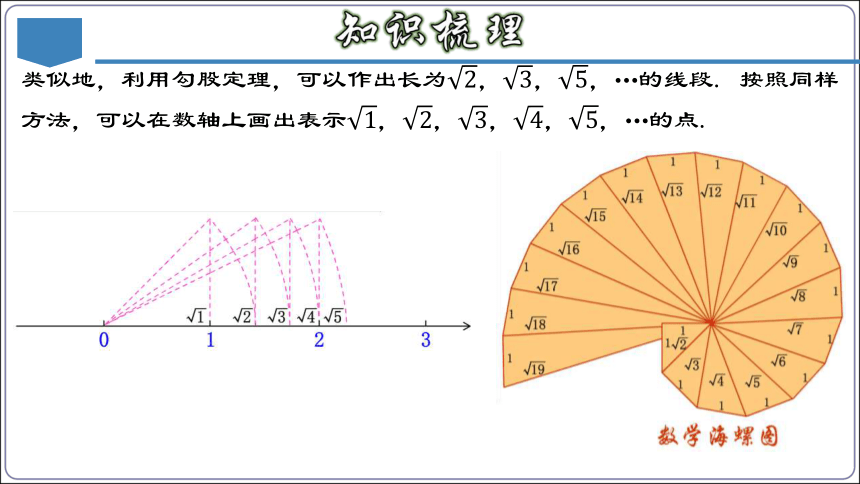
类似地,利用勾股定理,可以作出长为,,,…的线段. 按照同样方法,可以在数轴上画出表示,,,,,…的点.
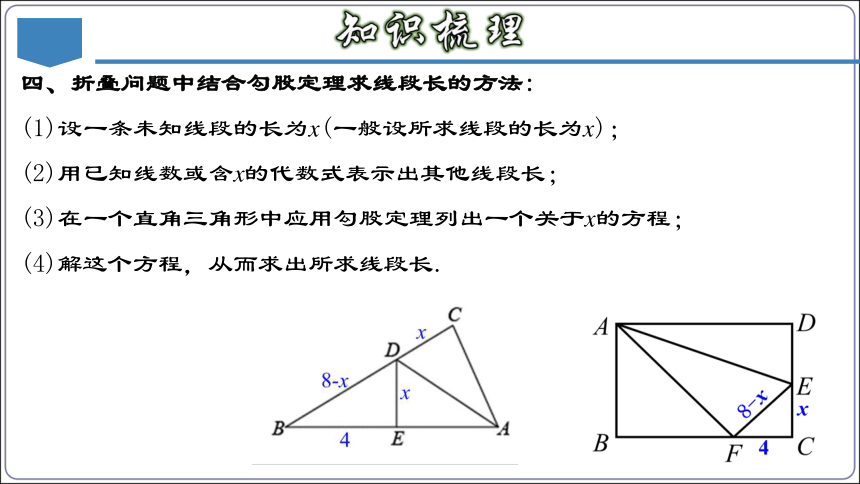
四、折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线数或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
五、原命题与逆命题
勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为 c,那么 a2+b2=c2.
勾股定理的逆定理:如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
六、勾股定理的逆定理
如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.
满足a2+b2=c2的三个正整数,称为勾股数.
常见勾股数:3,4,5;6,8,10;5,12,13;8,15,17;7,24,25等等.
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数. 如:3,4,5;6,8,10;9,12,15;12,16,20…
七、勾股数
01
勾股定理的简单应用
例1.在Rt△ABC中, ∠C=90°.
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
【点睛】已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
例2.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
∴AC×BC=AB×CD.
∴CD=.
【点睛】由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
例3.以直角三角形的三边为边向外作正方形,如图①所示,三个正方形的面积分别为S1,S2,S3, 则有S1+S2___S3(填“>”“=”“<”).
(1)分别以直角三角形的三边为直径向外作半圆,如图②所示,上述结论是否仍成立 说明理由.
解: (1) 成立.理由如下:
S1=×π(a)2=a2, S2=×π(b)2=b2
S3=×π(c)2=c2
∴a2+b2=c2,
∴S1+S2=S3
即(1)中的结论仍然成立.
=
例3.以直角三角形的三边为边向外作正方形,如图①所示,三个正方形的面积分别为S1,S2,S3, 则有S1+S2___S3(填“>”“=”“<”).
(2)分别以直角三角形的三边为斜边向外作等腰直角三角形,(1)中的结论仍成立吗(直接写出结论,无需证明)
解: (2) 成立.
=
(3)(变式拓展)如图③,图中数字代表正方形的面积,∠ACB=120°,求正方形P的面积.
解:(3)由题意得AC=2,BC=3.
作AD⊥BC,交BC的延长线于D.
∵∠ACB=120°
∴∠ACD=60°,∠DAC=30°
∴CD=AC=1
在Rt△ACD中,根据勾股定理得AD=
在Rt△ADB中,BD=BC+CD=3+1=4
根据勾股定理得AB2=AD2+BD2=3+16=19
∴正方形P的面积为AB2=19
【1-1】如图是我国古代著名的“赵爽弦图”的示意图,观察图形,可以验证的式子为( )
A.(a+b)(a-b)=a2-b2
B.(a+b)2=a2+2ab+b2
C.c2=a2+b2
D.(a-b)2=a2-2ab+b2
【1-2】在直角三角形中,若两直角边长分别为3和4,则斜边长是( )
A.5 B.7 C. D.或5
C
A
【1-3】设直角三角的两条直角边长分别为a和b,斜边长为c.
(1)已知a=5,c=10, 求b;
(2)已知a=8,b=15, 求c;
(3)已知c=2.5,b=1.5,求a.
解:(1)根据勾股定理得
(2)根据勾股定理得
(3)根据勾股定理得
【1-4】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
解:依题意,得
S1=SA+SB=122+162=144+256=400
S2=SC+SD=92+122=81+144=225
所以,SE=S1+S2=400+225=625
02
勾股定理的实际应用
例4.如图,有两棵树,一棵树高AC是10米,另一棵树高BD是4米,两树相距8米(即CD=8米),一只小鸟从一棵树的树梢A点处飞到另一棵树的树梢B点处,则小鸟至少要飞行多少米?
解:如图,大树高为AC=10米,小树高为BD=4米,
过点B作BE⊥AC于E,则四边形EBDC是长方形,连接AB,
∴EC=BD=4(米),EB=CD=8(米),
∴AE=AC-EC=10-4=6(米),
在中,(米),
答:小鸟至少飞行了10米.
例5.如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,航速是12海里/时,2小时后,两船同时到达了目的地.若C、B两岛的距离为30海里,问乙船的航速是多少?
解:根据题意得:,,
∴.
∴
∴.
∴乙船的航速是:(海里/时).
例6.有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2m,高AB是5m,π取3)
A
B
解:油罐的展开图如图,则AB′为梯子的最短距离.
∵AA′=2×3×2=12, A′B′=5,
在Rt△AA′B′中,由勾股定理得
即梯子最短需13米.
【分析】立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
【2-1】如图,在离水面高度为米的岸上,有人用绳子拉船靠岸,开始时绳子的长为米,此人以米每秒的速度收绳,秒后船移动到点的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
解:在中:
,米,米,
米,
此人以米每秒的速度收绳,秒后船移动到点的位置,
米,
米,
米,
答:船向岸边移动了米.
【2-2】如图,有一个圆柱体,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少 (π的值取3)
【2-2】如图,有一个圆柱体,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少 (π的值取3)
解:如图,将圆柱体的侧面展开得到Rt△ABC,则AB为这只蚂蚁爬行的最短路程.
BC=-×2π×3=9 (厘米)
根据勾股定理,得
AB2=AC2+BC2=122+92=152
AB=15(厘米)
答:这只蚂蚁爬行的最短路程是15厘米.
解:如图:过点A作,,
∵公路上A处点距离O点,距离MN为,
∴,
当火车到B点时对A处产生噪音影响,
此时,当货车到达D点后继续再运动时,对A处不再产生影响,此时,
∵,,,
【2-3】如图,铁路和公路在点O处交汇.公路上距离O点的A处与铁路的距离是.如果火车行驶时,周围以内会受到噪音的影响,那么火车在铁路上沿方向以的速度行驶时,A处受噪音影响的时间是多少?
【2-3】如图,铁路和公路在点O处交汇.公路上距离O点的A处与铁路的距离是.如果火车行驶时,周围以内会受到噪音的影响,那么火车在铁路上沿方向以的速度行驶时,A处受噪音影响的时间是多少?
∴由勾股定理得:,
,
∴,
∵,
∴A处受噪音影响的时间为:.
03
勾股定理的典型应用
例6.如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
【点睛】求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
例7.如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
【点睛】两点之间的距离公式:一般地,设平面上任意两点
例8.如图,在2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,求AB边上的高.
解:如图,过点C作CD⊥AB于点D.
D
【点睛】此类网格中求格点三角形的高的题,常用的方法是利用网格求面积,再用面积法求高.
例9.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理得 x2+42=(8-x)2,
解得 x=3.
即EC的长为3cm.
【3-1】如图,点A表示的实数是( )
A. B. C.- D.-
【3-2】如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
A.2 B. C. D.
C
D
【3-3】如图,将长方形纸片沿直线折叠,使点C落在边的中点处,点B落在点处,其中,求的长.
解:根据题意得:,,
∵为边的中点,
∴,
设,则,,
在中,,
∴,
解得:,
即.
【3-4】如图,在平面直角坐标系中,每个小正方形的边长都是1.
(1)画出关于对称的;
(2)的面积为 ;
(3)在上画出点P,使的周长最小,最小周长是________.
解:(1)如图,即为所求:
(2)
【3-4】如图,在平面直角坐标系中,每个小正方形的边长都是1.
(1)画出关于对称的;
(2)的面积为 ;
(3)在上画出点P,使的周长最小,最小周长是________.
(3)如图,连接交于点P,点P即为所求:
∵,
∴的最小周长
04
勾股定理的逆定理及其应用
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴ △ABC是直角三角形.
例10.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
例11.已知的三条边长分别为,且,,(,是正整数).是直角三角形吗?请证明你的判断.
解:是直角三角形.证明如下:
∵,,(,m,n是正整数),
∴
.
是直角三角形.
例12.如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
【4-1】下列各组数中,是勾股数的( )
A.0.3,0.4,0.5 B.9,16,25
C.5,12,13 D.10,15,18
【4-2】下面三角形中是直角三角形的有( )
①三角形三内角之比为1:2:3;
②三角形三内角之比为3:4:5;
③三角形三边之比为1:2:3;
④三角形三边之比为3:4:5.
A.1个 B.2个 C.3个 D.4个
C
B
【4-3】说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等.
解:(1)逆命题:内错角相等,两条直线平行,此命题成立;
(2)逆命题:如果两个实数的绝对值相等,那么这两个实数相等,此命题不成立;
(3)逆命题:对应角相等的两个三角形是全等三角形,此命题不成立.
【4-4】根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
解:(1)∵,,
∴,
∴以为边的三角形不是直角三角形;
(2)∵,,
∴,
∴以为边的三角形是直角三角形;
【4-4】根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
(3)∵,,
∴,
∴以为边的三角形是直角三角形;
(4)∵,,
∴,
∴以为边的三角形是直角三角形;
【4-4】根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
(5)∵,
∴设,
∵,,
∴,
∴以为边的三角形是直角三角形.
【4-5】已知中,、、所对边长分别为、、, 若、、三边满足,试判断的形状.
解:是直角三角形.
理由如下:
,
,,,
,,,
,,
,
是直角三角形.
05
勾股定理及其逆定理综合应用
例13.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(1)解:连接,
∵,,,
∴m,
∵,,
∴,
∴是直角三角形,且,
例13.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(2)求到的距离.
∴四边形花圃的面积
∴四边形花圃的面积是;
例13.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(2)求到的距离.
(2)过点C作于E,
∵,
∴,
∴,
∴到的距离是.
E
例14.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路,测得千米,千米,千米.求原来的路线的长.
解:∵千米,千米,千米,即,
∴,
∴是直角三角形,且,
∴,
∴,
例14.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路,测得千米,千米,千米.求原来的路线的长.
设,
∴,
∴,即,
解得:,
答:原来的路线的长为千米.
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
∵ 242+182=302,即PQ2+PR2=QR2
∴ ∠QPR=90°
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.
例15.如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【点睛】解决实际问题的步骤: 构建几何模型(从整体到局部); 标注有用信息,明确已知和所求; 应用数学知识求解.
例16.如图所示,在中,,且的周长为,点P从点A开始沿边向B点以每秒的速度移动;点Q从点B沿边向点C以每秒的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
解:设为,为,为,
∵的周长为,
∴,
即,
解得:,
∴,,,
∵,
例16.如图所示,在中,,且的周长为,点P从点A开始沿边向B点以每秒的速度移动;点Q从点B沿边向点C以每秒的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
∴是直角三角形,且.
经过3秒时,,,
又∵在中,,
∴,
即经过3秒时,P、Q两点间的距离为.
【5-1】如图,有一块地,已知∠ADC=90°,AD=4m, CD=3m,AB=13m,BC=12m.求这块地的面积.
解:连接AC.
在Rt△ACD中,根据勾股定理,
AC2=AD2+CD2=42+32=25
∴AC=5m
∵52+122=132
即AC2+BC2=AB2
∴∠ACB=90°
∴S阴=S△ABC-S△ACD=×5×12-×3×4=24(m2)
【5-2】如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
分析:根据勾股定理的逆定理得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三角形面积公式有
BC·AB=AC·BD,
即6×8=10BD,解得BD=.
在Rt△BCD中,
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
【5-3】某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离,以沙尘暴中心为圆心,周围以内都会受到沙尘暴影响.
(1)通过计算说明城镇C是否会受到影响;
(1)解:作于D,
在三角形中,,
∴是直角三角形,即,
,
,
解得∶千米,
所以,城镇C会受到影响.
D
【5-3】某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离,以沙尘暴中心为圆心,周围以内都会受到沙尘暴影响.
(2)若沙尘暴中心的移动速度为,则沙尘暴影响该城镇持续的时间有多长?
(2)解:设沙尘暴中心到点E处城镇C开始受到影响,此时千米,
到F处结束影响,此时千米,
,
千米,
受影响的时间为(小时)
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
知识网络
学习目标
知识梳理
迁移应用
2024春人教版八(下)数学同步精品课件
考点解析
考点梳理
章节复习
第十七章 勾股定理
1.复习与回顾本章的重要知识点; (重点)
2.勾股定理及其逆定理的用途和相互关系;
3.总结本章的重要思想方法及其应用;(难点)
4.勾股定理及逆定理的综合运用.(难点)
一、勾股定理
勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
利用
构造
解决
二、勾股定理的实际应用
三、利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
类似地,利用勾股定理,可以作出长为,,,…的线段. 按照同样方法,可以在数轴上画出表示,,,,,…的点.
四、折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线数或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
五、原命题与逆命题
勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为 c,那么 a2+b2=c2.
勾股定理的逆定理:如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
六、勾股定理的逆定理
如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.
满足a2+b2=c2的三个正整数,称为勾股数.
常见勾股数:3,4,5;6,8,10;5,12,13;8,15,17;7,24,25等等.
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数. 如:3,4,5;6,8,10;9,12,15;12,16,20…
七、勾股数
01
勾股定理的简单应用
例1.在Rt△ABC中, ∠C=90°.
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
【点睛】已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
例2.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
∴AC×BC=AB×CD.
∴CD=.
【点睛】由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
例3.以直角三角形的三边为边向外作正方形,如图①所示,三个正方形的面积分别为S1,S2,S3, 则有S1+S2___S3(填“>”“=”“<”).
(1)分别以直角三角形的三边为直径向外作半圆,如图②所示,上述结论是否仍成立 说明理由.
解: (1) 成立.理由如下:
S1=×π(a)2=a2, S2=×π(b)2=b2
S3=×π(c)2=c2
∴a2+b2=c2,
∴S1+S2=S3
即(1)中的结论仍然成立.
=
例3.以直角三角形的三边为边向外作正方形,如图①所示,三个正方形的面积分别为S1,S2,S3, 则有S1+S2___S3(填“>”“=”“<”).
(2)分别以直角三角形的三边为斜边向外作等腰直角三角形,(1)中的结论仍成立吗(直接写出结论,无需证明)
解: (2) 成立.
=
(3)(变式拓展)如图③,图中数字代表正方形的面积,∠ACB=120°,求正方形P的面积.
解:(3)由题意得AC=2,BC=3.
作AD⊥BC,交BC的延长线于D.
∵∠ACB=120°
∴∠ACD=60°,∠DAC=30°
∴CD=AC=1
在Rt△ACD中,根据勾股定理得AD=
在Rt△ADB中,BD=BC+CD=3+1=4
根据勾股定理得AB2=AD2+BD2=3+16=19
∴正方形P的面积为AB2=19
【1-1】如图是我国古代著名的“赵爽弦图”的示意图,观察图形,可以验证的式子为( )
A.(a+b)(a-b)=a2-b2
B.(a+b)2=a2+2ab+b2
C.c2=a2+b2
D.(a-b)2=a2-2ab+b2
【1-2】在直角三角形中,若两直角边长分别为3和4,则斜边长是( )
A.5 B.7 C. D.或5
C
A
【1-3】设直角三角的两条直角边长分别为a和b,斜边长为c.
(1)已知a=5,c=10, 求b;
(2)已知a=8,b=15, 求c;
(3)已知c=2.5,b=1.5,求a.
解:(1)根据勾股定理得
(2)根据勾股定理得
(3)根据勾股定理得
【1-4】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
解:依题意,得
S1=SA+SB=122+162=144+256=400
S2=SC+SD=92+122=81+144=225
所以,SE=S1+S2=400+225=625
02
勾股定理的实际应用
例4.如图,有两棵树,一棵树高AC是10米,另一棵树高BD是4米,两树相距8米(即CD=8米),一只小鸟从一棵树的树梢A点处飞到另一棵树的树梢B点处,则小鸟至少要飞行多少米?
解:如图,大树高为AC=10米,小树高为BD=4米,
过点B作BE⊥AC于E,则四边形EBDC是长方形,连接AB,
∴EC=BD=4(米),EB=CD=8(米),
∴AE=AC-EC=10-4=6(米),
在中,(米),
答:小鸟至少飞行了10米.
例5.如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,航速是12海里/时,2小时后,两船同时到达了目的地.若C、B两岛的距离为30海里,问乙船的航速是多少?
解:根据题意得:,,
∴.
∴
∴.
∴乙船的航速是:(海里/时).
例6.有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2m,高AB是5m,π取3)
A
B
解:油罐的展开图如图,则AB′为梯子的最短距离.
∵AA′=2×3×2=12, A′B′=5,
在Rt△AA′B′中,由勾股定理得
即梯子最短需13米.
【分析】立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
【2-1】如图,在离水面高度为米的岸上,有人用绳子拉船靠岸,开始时绳子的长为米,此人以米每秒的速度收绳,秒后船移动到点的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
解:在中:
,米,米,
米,
此人以米每秒的速度收绳,秒后船移动到点的位置,
米,
米,
米,
答:船向岸边移动了米.
【2-2】如图,有一个圆柱体,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少 (π的值取3)
【2-2】如图,有一个圆柱体,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少 (π的值取3)
解:如图,将圆柱体的侧面展开得到Rt△ABC,则AB为这只蚂蚁爬行的最短路程.
BC=-×2π×3=9 (厘米)
根据勾股定理,得
AB2=AC2+BC2=122+92=152
AB=15(厘米)
答:这只蚂蚁爬行的最短路程是15厘米.
解:如图:过点A作,,
∵公路上A处点距离O点,距离MN为,
∴,
当火车到B点时对A处产生噪音影响,
此时,当货车到达D点后继续再运动时,对A处不再产生影响,此时,
∵,,,
【2-3】如图,铁路和公路在点O处交汇.公路上距离O点的A处与铁路的距离是.如果火车行驶时,周围以内会受到噪音的影响,那么火车在铁路上沿方向以的速度行驶时,A处受噪音影响的时间是多少?
【2-3】如图,铁路和公路在点O处交汇.公路上距离O点的A处与铁路的距离是.如果火车行驶时,周围以内会受到噪音的影响,那么火车在铁路上沿方向以的速度行驶时,A处受噪音影响的时间是多少?
∴由勾股定理得:,
,
∴,
∵,
∴A处受噪音影响的时间为:.
03
勾股定理的典型应用
例6.如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
【点睛】求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
例7.如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
【点睛】两点之间的距离公式:一般地,设平面上任意两点
例8.如图,在2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,求AB边上的高.
解:如图,过点C作CD⊥AB于点D.
D
【点睛】此类网格中求格点三角形的高的题,常用的方法是利用网格求面积,再用面积法求高.
例9.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理得 x2+42=(8-x)2,
解得 x=3.
即EC的长为3cm.
【3-1】如图,点A表示的实数是( )
A. B. C.- D.-
【3-2】如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
A.2 B. C. D.
C
D
【3-3】如图,将长方形纸片沿直线折叠,使点C落在边的中点处,点B落在点处,其中,求的长.
解:根据题意得:,,
∵为边的中点,
∴,
设,则,,
在中,,
∴,
解得:,
即.
【3-4】如图,在平面直角坐标系中,每个小正方形的边长都是1.
(1)画出关于对称的;
(2)的面积为 ;
(3)在上画出点P,使的周长最小,最小周长是________.
解:(1)如图,即为所求:
(2)
【3-4】如图,在平面直角坐标系中,每个小正方形的边长都是1.
(1)画出关于对称的;
(2)的面积为 ;
(3)在上画出点P,使的周长最小,最小周长是________.
(3)如图,连接交于点P,点P即为所求:
∵,
∴的最小周长
04
勾股定理的逆定理及其应用
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴ △ABC是直角三角形.
例10.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
例11.已知的三条边长分别为,且,,(,是正整数).是直角三角形吗?请证明你的判断.
解:是直角三角形.证明如下:
∵,,(,m,n是正整数),
∴
.
是直角三角形.
例12.如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
【4-1】下列各组数中,是勾股数的( )
A.0.3,0.4,0.5 B.9,16,25
C.5,12,13 D.10,15,18
【4-2】下面三角形中是直角三角形的有( )
①三角形三内角之比为1:2:3;
②三角形三内角之比为3:4:5;
③三角形三边之比为1:2:3;
④三角形三边之比为3:4:5.
A.1个 B.2个 C.3个 D.4个
C
B
【4-3】说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等.
解:(1)逆命题:内错角相等,两条直线平行,此命题成立;
(2)逆命题:如果两个实数的绝对值相等,那么这两个实数相等,此命题不成立;
(3)逆命题:对应角相等的两个三角形是全等三角形,此命题不成立.
【4-4】根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
解:(1)∵,,
∴,
∴以为边的三角形不是直角三角形;
(2)∵,,
∴,
∴以为边的三角形是直角三角形;
【4-4】根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
(3)∵,,
∴,
∴以为边的三角形是直角三角形;
(4)∵,,
∴,
∴以为边的三角形是直角三角形;
【4-4】根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
(5)∵,
∴设,
∵,,
∴,
∴以为边的三角形是直角三角形.
【4-5】已知中,、、所对边长分别为、、, 若、、三边满足,试判断的形状.
解:是直角三角形.
理由如下:
,
,,,
,,,
,,
,
是直角三角形.
05
勾股定理及其逆定理综合应用
例13.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(1)解:连接,
∵,,,
∴m,
∵,,
∴,
∴是直角三角形,且,
例13.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(2)求到的距离.
∴四边形花圃的面积
∴四边形花圃的面积是;
例13.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(2)求到的距离.
(2)过点C作于E,
∵,
∴,
∴,
∴到的距离是.
E
例14.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路,测得千米,千米,千米.求原来的路线的长.
解:∵千米,千米,千米,即,
∴,
∴是直角三角形,且,
∴,
∴,
例14.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路,测得千米,千米,千米.求原来的路线的长.
设,
∴,
∴,即,
解得:,
答:原来的路线的长为千米.
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
∵ 242+182=302,即PQ2+PR2=QR2
∴ ∠QPR=90°
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.
例15.如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【点睛】解决实际问题的步骤: 构建几何模型(从整体到局部); 标注有用信息,明确已知和所求; 应用数学知识求解.
例16.如图所示,在中,,且的周长为,点P从点A开始沿边向B点以每秒的速度移动;点Q从点B沿边向点C以每秒的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
解:设为,为,为,
∵的周长为,
∴,
即,
解得:,
∴,,,
∵,
例16.如图所示,在中,,且的周长为,点P从点A开始沿边向B点以每秒的速度移动;点Q从点B沿边向点C以每秒的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
∴是直角三角形,且.
经过3秒时,,,
又∵在中,,
∴,
即经过3秒时,P、Q两点间的距离为.
【5-1】如图,有一块地,已知∠ADC=90°,AD=4m, CD=3m,AB=13m,BC=12m.求这块地的面积.
解:连接AC.
在Rt△ACD中,根据勾股定理,
AC2=AD2+CD2=42+32=25
∴AC=5m
∵52+122=132
即AC2+BC2=AB2
∴∠ACB=90°
∴S阴=S△ABC-S△ACD=×5×12-×3×4=24(m2)
【5-2】如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
分析:根据勾股定理的逆定理得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三角形面积公式有
BC·AB=AC·BD,
即6×8=10BD,解得BD=.
在Rt△BCD中,
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
【5-3】某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离,以沙尘暴中心为圆心,周围以内都会受到沙尘暴影响.
(1)通过计算说明城镇C是否会受到影响;
(1)解:作于D,
在三角形中,,
∴是直角三角形,即,
,
,
解得∶千米,
所以,城镇C会受到影响.
D
【5-3】某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离,以沙尘暴中心为圆心,周围以内都会受到沙尘暴影响.
(2)若沙尘暴中心的移动速度为,则沙尘暴影响该城镇持续的时间有多长?
(2)解:设沙尘暴中心到点E处城镇C开始受到影响,此时千米,
到F处结束影响,此时千米,
,
千米,
受影响的时间为(小时)
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
