17.1.1 勾股定理(第一课时)教学设计【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 17.1.1 勾股定理(第一课时)教学设计【2024春人教八下数学同步优质教案】 |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 20:29:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
17.1.1 勾股定理 教学设计
一、教学目标:
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.
2.会用勾股定理进行简单的计算 .
二、教学重、难点:
重点:掌握勾股定理,并运用它解决简单的计算题.
难点:了解利用拼摆验证勾股定理的方法.
三、教学过程:
情境引入
人类一直想要弄清楚其他星球上是否存在着“人”,并试图与“他们”取得联系. 那么我们怎样才能与“外星人”接触呢?
曾经有科学家建议用“勾股定理”的图来作为与“外星人”联系的信号.
如图,强大的台风使得一棵大树在离地面6米处折断倒下,大树顶部落在离大树底部8米处. 大树折断之前有多高?
想一想, 你需要求哪些线段长度、这些长度确定吗?
知识精讲
邮票赏析
邮票的秘密:观察这枚邮票图案小方格的个数,你有什么发现?
32+42=52
相传2500多年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.我们也来观察一下地面的图案,看看能从中发现什么数量关系?
问题1:试问正方形A、B、C面积之间有什么样的数量关系?
问题2:图中正方形A、B、C所围成的直角三角形三边之间有什么特殊数量关系?
猜想:斜边的平方等于两直角边的平方和.
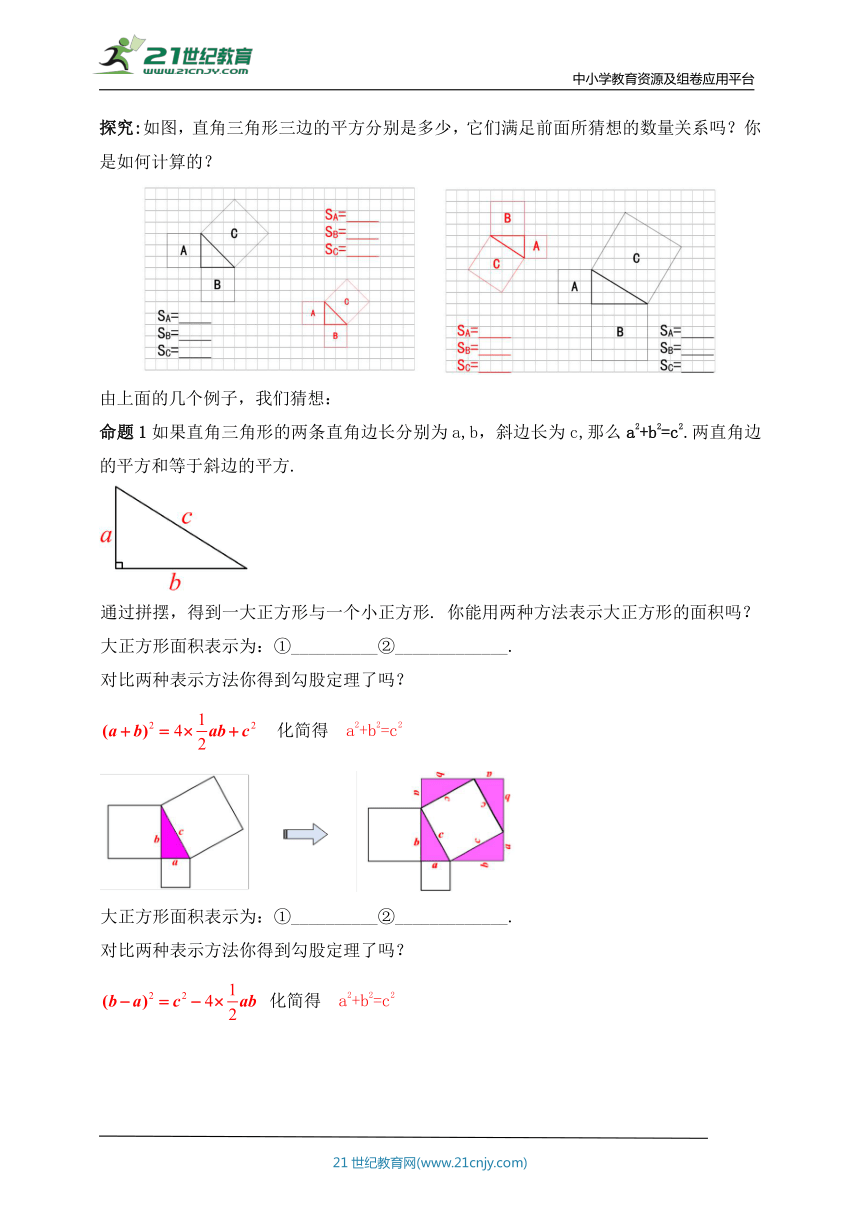
探究:如图,直角三角形三边的平方分别是多少,它们满足前面所猜想的数量关系吗?你是如何计算的?
由上面的几个例子,我们猜想:
命题1如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
通过拼摆,得到一大正方形与一个小正方形. 你能用两种方法表示大正方形的面积吗?
大正方形面积表示为:①__________②_____________.
对比两种表示方法你得到勾股定理了吗?
化简得 a2+b2=c2
大正方形面积表示为:①__________②_____________.
对比两种表示方法你得到勾股定理了吗?
化简得 a2+b2=c2
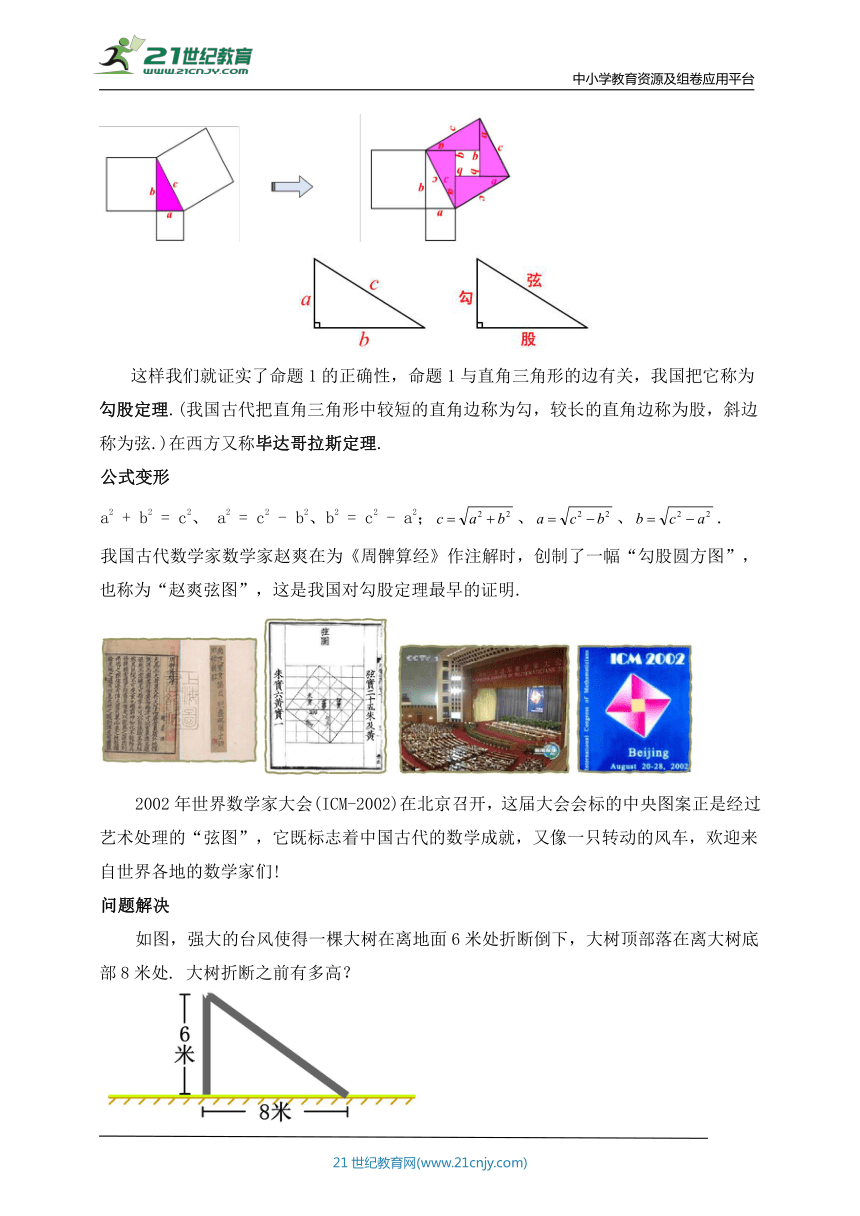
这样我们就证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称为勾股定理.(我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.)在西方又称毕达哥拉斯定理.
公式变形
a2 + b2 = c2、 a2 = c2 - b2、b2 = c2 - a2;、、.
我国古代数学家数学家赵爽在为《周髀算经》作注解时,创制了一幅“勾股圆方图”,也称为“赵爽弦图”,这是我国对勾股定理最早的证明.
2002年世界数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
问题解决
如图,强大的台风使得一棵大树在离地面6米处折断倒下,大树顶部落在离大树底部8米处. 大树折断之前有多高?
解:,
所以,大树折断之前的高度为:6+10=16(米).
典例解析
例1.如图,在Rt△ABC中,∠C=90°.
(1)若a=b=5,求c; (2)若a=1,c=2,求b.
解:(1)根据勾股定理得
(2)根据勾股定理得
【针对练习】设直角三角的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;(2)已知a=5,b=12,求c;(3)已知c=25,b=15,求a.
解:(1)根据勾股定理得 ;
(2)根据勾股定理得;
(3)根据勾股定理得.
例2.在Rt△ABC中, ∠C=90°.
(1)若a:b=1:2 ,c=5,求a; (2)若b=15,∠A=30°,求a,c.
解:(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,解得
【点睛】已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
例3.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图,
当BC为斜边时,如图,
【点睛】当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
例4.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,即 AB=5.
根据三角形面积公式,
∴AC×BC=AB×CD.
∴CD=.
【点睛】由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.如图是我国古代著名的“赵爽弦图”的示意图,观察图形,可以验证的式子为( )
A.(a+b)(a-b)=a2-b2 B.(a+b)2=a2+2ab+b2 C.c2=a2+b2 D.(a-b)2=a2-2ab+b2
2.在直角三角形中,若两直角边长分别为3和4,则斜边长是( )
A.5 B.7 C. D.或5
3.在直角三角形中,若两边长分别为3和4,则第三边长为( )
A.1 B.5 C. D.或5
4.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.76 D.80
5.如图,网格的边长为1,在△ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
6.如图(1),三个正方形中的两个的面积S1=20,S2=60,则另一个的面积S3为_____.
7.如图(2),在Rt△ABC中,∠ACB=90°,两个正方形的面积如图所示,则△ABC的周长是_____.
8.如图(3),点E在正方形ABCD的边AB上.若EB=1, EC=2,则正方形ABCD的面积为_____.
9.点P(a,3)在第二象限,且到原点的距离是5,则a=____.
10.如图①,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图②放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图②中阴影部分面积为______.
11.设直角三角的两条直角边长分别为a和b,斜边长为c.
(1)已知a=5,c=10, 求b;
(2)已知a=8,b=15, 求c;
(3)已知c=2.5,b=1.5,求a.
12.如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
13.以直角三角形的三边为边向外作正方形,如图①所示,三个正方形的面积分别为S1,S2,S3, 则有S1+S2___S3(填“>”“=”“<”).
(1)分别以直角三角形的三边为直径向外作半圆,如图②所示,上述结论是否仍成立 说明理由.
(2)分别以直角三角形的三边为斜边向外作等腰直角三角形,(1)中的结论仍成立吗(直接写出结论,无需证明)
(3)(变式拓展)如图③,图中数字代表正方形的面积,∠ACB=120°,求正方形P的面积.
【参考答案】
C
A
D
C
D
80
24
3
-4
4
11.解:(1)根据勾股定理得
(2)根据勾股定理得
(3)根据勾股定理得
12.解:依题意,得
S1=SA+SB=122+162=144+256=400
S2=SC+SD=92+122=81+144=225
所以,SE=S1+S2=400+225=625
13.解: (1) 成立.理由如下:
S1=×π(a)2=a2, S2=×π(b)2=b2
S3=×π(c)2=c2
∴a2+b2=c2,
∴S1+S2=S3
即(1)中的结论仍然成立.
(2) 成立.
(3)由题意得AC=2,BC=3.
作AD⊥BC,交BC的延长线于D.
∵∠ACB=120°
∴∠ACD=60°,∠DAC=30°
∴CD=AC=1
在Rt△ACD中,根据勾股定理得AD=
在Rt△ADB中,BD=BC+CD=3+1=4
根据勾股定理得AB2=AD2+BD2=3+16=19
∴正方形P的面积为AB2=19
四、教学反思:
课堂教学中,要注意调动学生的积极性.让学生满怀激情地投入到学习中,提高课堂效率.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,设计一些拼图活动,并自制精巧的课件让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究突破本节课的难点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
17.1.1 勾股定理 教学设计
一、教学目标:
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.
2.会用勾股定理进行简单的计算 .
二、教学重、难点:
重点:掌握勾股定理,并运用它解决简单的计算题.
难点:了解利用拼摆验证勾股定理的方法.
三、教学过程:
情境引入
人类一直想要弄清楚其他星球上是否存在着“人”,并试图与“他们”取得联系. 那么我们怎样才能与“外星人”接触呢?
曾经有科学家建议用“勾股定理”的图来作为与“外星人”联系的信号.
如图,强大的台风使得一棵大树在离地面6米处折断倒下,大树顶部落在离大树底部8米处. 大树折断之前有多高?
想一想, 你需要求哪些线段长度、这些长度确定吗?
知识精讲
邮票赏析
邮票的秘密:观察这枚邮票图案小方格的个数,你有什么发现?
32+42=52
相传2500多年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.我们也来观察一下地面的图案,看看能从中发现什么数量关系?
问题1:试问正方形A、B、C面积之间有什么样的数量关系?
问题2:图中正方形A、B、C所围成的直角三角形三边之间有什么特殊数量关系?
猜想:斜边的平方等于两直角边的平方和.
探究:如图,直角三角形三边的平方分别是多少,它们满足前面所猜想的数量关系吗?你是如何计算的?
由上面的几个例子,我们猜想:
命题1如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
通过拼摆,得到一大正方形与一个小正方形. 你能用两种方法表示大正方形的面积吗?
大正方形面积表示为:①__________②_____________.
对比两种表示方法你得到勾股定理了吗?
化简得 a2+b2=c2
大正方形面积表示为:①__________②_____________.
对比两种表示方法你得到勾股定理了吗?
化简得 a2+b2=c2
这样我们就证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称为勾股定理.(我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.)在西方又称毕达哥拉斯定理.
公式变形
a2 + b2 = c2、 a2 = c2 - b2、b2 = c2 - a2;、、.
我国古代数学家数学家赵爽在为《周髀算经》作注解时,创制了一幅“勾股圆方图”,也称为“赵爽弦图”,这是我国对勾股定理最早的证明.
2002年世界数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
问题解决
如图,强大的台风使得一棵大树在离地面6米处折断倒下,大树顶部落在离大树底部8米处. 大树折断之前有多高?
解:,
所以,大树折断之前的高度为:6+10=16(米).
典例解析
例1.如图,在Rt△ABC中,∠C=90°.
(1)若a=b=5,求c; (2)若a=1,c=2,求b.
解:(1)根据勾股定理得
(2)根据勾股定理得
【针对练习】设直角三角的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;(2)已知a=5,b=12,求c;(3)已知c=25,b=15,求a.
解:(1)根据勾股定理得 ;
(2)根据勾股定理得;
(3)根据勾股定理得.
例2.在Rt△ABC中, ∠C=90°.
(1)若a:b=1:2 ,c=5,求a; (2)若b=15,∠A=30°,求a,c.
解:(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,解得
【点睛】已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
例3.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图,
当BC为斜边时,如图,
【点睛】当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
例4.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,即 AB=5.
根据三角形面积公式,
∴AC×BC=AB×CD.
∴CD=.
【点睛】由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.如图是我国古代著名的“赵爽弦图”的示意图,观察图形,可以验证的式子为( )
A.(a+b)(a-b)=a2-b2 B.(a+b)2=a2+2ab+b2 C.c2=a2+b2 D.(a-b)2=a2-2ab+b2
2.在直角三角形中,若两直角边长分别为3和4,则斜边长是( )
A.5 B.7 C. D.或5
3.在直角三角形中,若两边长分别为3和4,则第三边长为( )
A.1 B.5 C. D.或5
4.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.76 D.80
5.如图,网格的边长为1,在△ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
6.如图(1),三个正方形中的两个的面积S1=20,S2=60,则另一个的面积S3为_____.
7.如图(2),在Rt△ABC中,∠ACB=90°,两个正方形的面积如图所示,则△ABC的周长是_____.
8.如图(3),点E在正方形ABCD的边AB上.若EB=1, EC=2,则正方形ABCD的面积为_____.
9.点P(a,3)在第二象限,且到原点的距离是5,则a=____.
10.如图①,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图②放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图②中阴影部分面积为______.
11.设直角三角的两条直角边长分别为a和b,斜边长为c.
(1)已知a=5,c=10, 求b;
(2)已知a=8,b=15, 求c;
(3)已知c=2.5,b=1.5,求a.
12.如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
13.以直角三角形的三边为边向外作正方形,如图①所示,三个正方形的面积分别为S1,S2,S3, 则有S1+S2___S3(填“>”“=”“<”).
(1)分别以直角三角形的三边为直径向外作半圆,如图②所示,上述结论是否仍成立 说明理由.
(2)分别以直角三角形的三边为斜边向外作等腰直角三角形,(1)中的结论仍成立吗(直接写出结论,无需证明)
(3)(变式拓展)如图③,图中数字代表正方形的面积,∠ACB=120°,求正方形P的面积.
【参考答案】
C
A
D
C
D
80
24
3
-4
4
11.解:(1)根据勾股定理得
(2)根据勾股定理得
(3)根据勾股定理得
12.解:依题意,得
S1=SA+SB=122+162=144+256=400
S2=SC+SD=92+122=81+144=225
所以,SE=S1+S2=400+225=625
13.解: (1) 成立.理由如下:
S1=×π(a)2=a2, S2=×π(b)2=b2
S3=×π(c)2=c2
∴a2+b2=c2,
∴S1+S2=S3
即(1)中的结论仍然成立.
(2) 成立.
(3)由题意得AC=2,BC=3.
作AD⊥BC,交BC的延长线于D.
∵∠ACB=120°
∴∠ACD=60°,∠DAC=30°
∴CD=AC=1
在Rt△ACD中,根据勾股定理得AD=
在Rt△ADB中,BD=BC+CD=3+1=4
根据勾股定理得AB2=AD2+BD2=3+16=19
∴正方形P的面积为AB2=19
四、教学反思:
课堂教学中,要注意调动学生的积极性.让学生满怀激情地投入到学习中,提高课堂效率.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,设计一些拼图活动,并自制精巧的课件让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究突破本节课的难点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
