17.2.1 勾股定理的逆定理(第一课时)教学设计【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 17.2.1 勾股定理的逆定理(第一课时)教学设计【2024春人教八下数学同步优质教案】 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
17.2.1 勾股定理的逆定理 教学设计
一、教学目标:
1.掌握勾股定理逆定理的概念并理解互逆命题、定理的概念、关系及勾股数.
2.能证明勾股定理的逆定理,能利用勾股定理的逆定理判断一个三角形是直角三角形.
二、教学重、难点:
重点:灵活运用勾股定理及其逆定理解决问题.
难点:灵活运用勾股定理及其逆定理解决问题.
三、教学过程:
复习回顾
1.勾股定理的内容是什么
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
2.求以线段a、b为直角边的直角三角形的斜边c的长.
① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.
思考:以前我们已经学过了通过角的关系来确定直角三角形,可不可以通过边来确定直角三角形呢?
情境引入
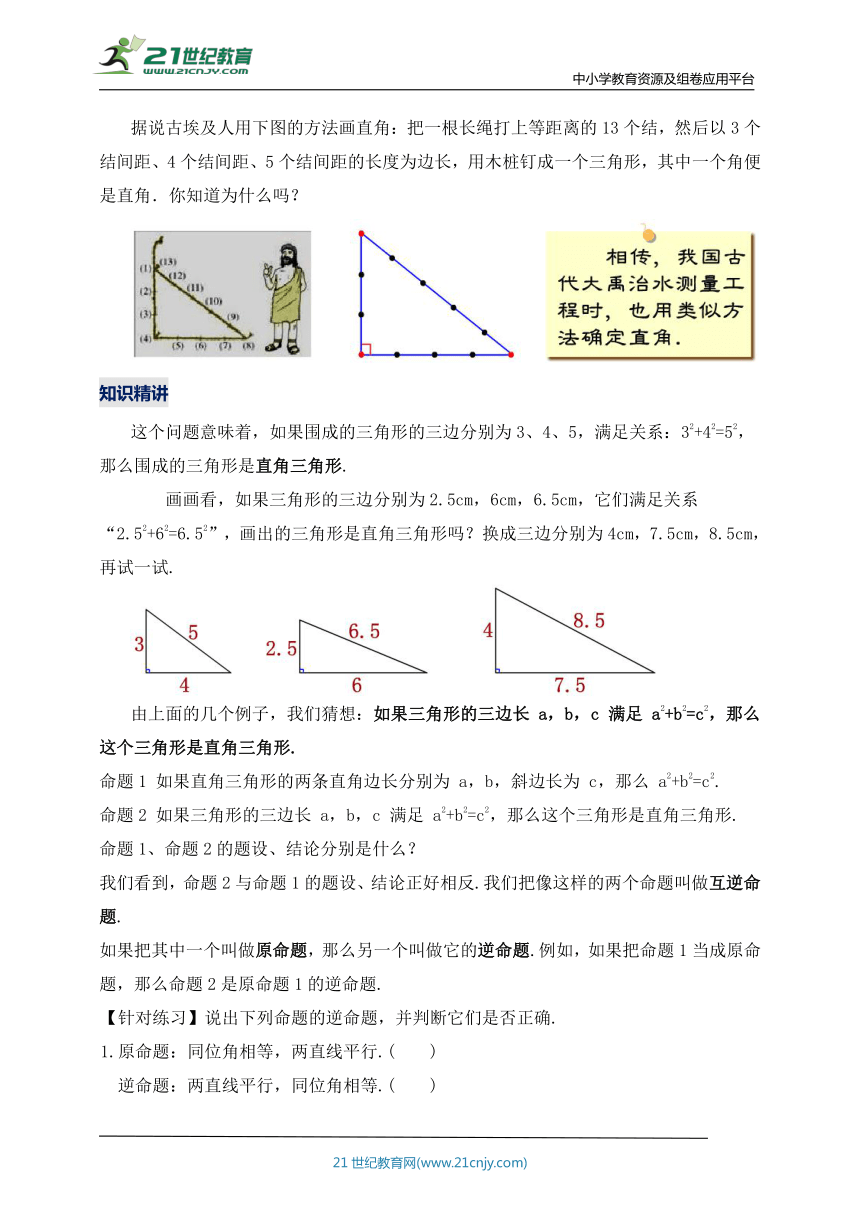
据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你知道为什么吗?
知识精讲
这个问题意味着,如果围成的三角形的三边分别为3、4、5,满足关系:32+42=52,那么围成的三角形是直角三角形.
画画看,如果三角形的三边分别为2.5cm,6cm,6.5cm,它们满足关系“2.52+62=6.52”,画出的三角形是直角三角形吗?换成三边分别为4cm,7.5cm,8.5cm,再试一试.
由上面的几个例子,我们猜想:如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
命题1 如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么 a2+b2=c2.
命题2 如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
命题1、命题2的题设、结论分别是什么?
我们看到,命题2与命题1的题设、结论正好相反.我们把像这样的两个命题叫做互逆命题.
如果把其中一个叫做原命题,那么另一个叫做它的逆命题.例如,如果把命题1当成原命题,那么命题2是原命题1的逆命题.
【针对练习】说出下列命题的逆命题,并判断它们是否正确.
1.原命题:同位角相等,两直线平行.( )
逆命题:两直线平行,同位角相等.( )
2.原命题:对顶角相等.( )
逆命题:相等的角是对顶角.( )
3.原命题:线段垂直平分线上的点与这条线段两个端点的距离相等.( )
逆命题:与线段两个端点距离相等的点在这条线段的垂直平分线上.( )
4.原命题:角平分线上的点到角的两边的距离相等.( )
逆命题:角的内部到角的两边的距离相等的点在角的平分线上.( )
在图(1)中,已知△ABC的三边长分别为a,b,c,且满足a2+b2=c2,要证△ABC一定是直角三角形.我们可以先画一个两条直角边长分别为a,b的Rt△A′B′C′如图(2),如果△ABC与Rt△A′B′C′全等,那么△ABC就是一个直角三角形.
已知△ABC,BC=a,AC=b,AB=c,且a2+b2=c2.
求证:△ABC是直角三角形.
证明:作Rt△A′B′C′,使B′C′=a,A′C′=b,∠C′=90°.
根据勾股定理,A′B′2=B′C′2+A′C′2=a2+b2=c2
∴ A′B′=c
在△ABC和△A′B′C′中,
BC=a=B′C′,AC=b=A′C′,AB=c=A′B′
∴ △ABC≌△A′B′C′(SSS)
∴ ∠C=∠C′=90°
即△ABC是直角三角形.
【归纳】勾股定理 如果直角三角形的两条直角边长分别为a,b,斜边长为 c,那么 a2+b2=c2.
勾股定理的逆定理 如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
典例解析
例1 判断由线段a,b,c组成的三角形是不是直角三角形:
(1) a=15,b=8,c=17;(2) a=13,b=14,c=15.
解:(1)∵ 152+82=225+64=289,172=289
∴ 152+82=172,根据勾股定理的逆定理,这个三角形是直角三角形.
(2)∵ 132+142=169+196=365,152=225
∴ 132+142≠152,根据勾股定理,这个三角形不是直角三角形.
【点睛】根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
【归纳】像15,8,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.
常见勾股数:3,4,5;6,8,10;5,12,13;8,15,17;7,24,25等等.
勾股数拓展性质:一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数. 如:3,4,5;6,8,10;9,12,15;12,16,20…
【针对练习】若△ABC的三边a,b,c满足 a:b: c=3:4:5,是判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
【点睛】已知三角形三边的比例关系判断三角形形状:先设出参数,表示出三条边的长,再用勾股定理的逆定理判断其是否是直角三角形.如果此直角三角形的三边中有两个相同的数,那么该三角形还是等腰三角形.
例2.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴ △ABC是直角三角形.
【针对练习】若△ABC的三边a,b,c,且a+b=4,ab=1,c=,试说明△ABC是直角三角形.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
例3.已知的三条边长分别为,且,,(,是正整数).是直角三角形吗?请证明你的判断.
解:是直角三角形.证明如下:
∵,,(,m,n是正整数),
∴
.
是直角三角形.
【针对练习】已知的三边,,.
求证:是直角三角形.
解:∵的三边,,,
而,,,
∵,
∴,
即,
∴是直角三角形.
例4.已知,,.
(1)在坐标系中描出各点,画出三角形;
(2)求三角形的面积;
(3)仅用无刻度的直尺作出边上的高,并直接写出的长.(保留作图痕迹)
解:(1)如图所示:
(2)
(3)如图所示的线段即所求作的高.
由图可得:
,
∴
∴是直角三角形,
∴
∴
∴
∴
例5.如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.下列各组数中,是勾股数的( )
A.0.3,0.4,0.5 B.9,16,25 C.5,12,13 D.10,15,18
2.下面三角形中是直角三角形的有( )
①三角形三内角之比为1:2:3;
②三角形三内角之比为3:4:5;
③三角形三边之比为1:2:3;
④三角形三边之比为3:4:5.
A.1个 B.2个 C.3个 D.4个
3.下列命题中,逆命题为真命题的是( )
A.全等三角形的对应角相等 B.等角对等边
C.若a=b,则|a|=|b| D.若ac24.一个三角形的三边的长分别是3,4,5,则这个三角形最长边上的高是 ( )
A.4 B.3 C.2.5 D.2.4
4.已知一个三角形的三边长分别为2、3、则这个三角形的面积是_____.
5若△ABC的三边a、b、c满足(a-b)(a2+b2-c2)=0,则△ABC是__________________________.
6.命题 “如果a+b=0,那么a=0,b=0” 的逆命题是_______________________,它是____命题.
7.根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
8.说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等.
9.已知中,、、所对边长分别为、、, 若、、三边满足,试判断的形状.
10.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,的顶点都在格点上.
(1)求的度数;
(2)求的面积.
【参考答案】
C
B
B
D
3
等腰三角形或直角三角形
如果a=0,b=0,那么a+b=0;真
8.解:(1)∵,,
∴,
∴以为边的三角形不是直角三角形;
(2)∵,,
∴,
∴以为边的三角形是直角三角形;
(3)∵,,
∴,
∴以为边的三角形是直角三角形;
(4)∵,,
∴,
∴以为边的三角形是直角三角形;
(5)∵,
∴设,
∵,,
∴,
∴以为边的三角形是直角三角形.
8.解:(1)逆命题:内错角相等,两条直线平行,此命题成立;
(2)逆命题:如果两个实数的绝对值相等,那么这两个实数相等,此命题不成立;
(3)逆命题:对应角相等的两个三角形是全等三角形,此命题不成立.
9.解:是直角三角形.
理由如下:
,
,,,
,,,
,,
,
是直角三角形.
10.解:(1),
,
,
∵,
∴为直角三角形,
∴,
∵,
∴;
(2).
四、教学反思:
在本课时教学过程中,应以师生共同探讨为主. 激励学生回答问题,激发学生的求知欲.课堂上师生互动频繁,既保证课堂教学进度,又提高课堂学习效率. 学生在探讨过程中也加深了对知识的理解和记忆.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
17.2.1 勾股定理的逆定理 教学设计
一、教学目标:
1.掌握勾股定理逆定理的概念并理解互逆命题、定理的概念、关系及勾股数.
2.能证明勾股定理的逆定理,能利用勾股定理的逆定理判断一个三角形是直角三角形.
二、教学重、难点:
重点:灵活运用勾股定理及其逆定理解决问题.
难点:灵活运用勾股定理及其逆定理解决问题.
三、教学过程:
复习回顾
1.勾股定理的内容是什么
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
2.求以线段a、b为直角边的直角三角形的斜边c的长.
① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.
思考:以前我们已经学过了通过角的关系来确定直角三角形,可不可以通过边来确定直角三角形呢?
情境引入
据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你知道为什么吗?
知识精讲
这个问题意味着,如果围成的三角形的三边分别为3、4、5,满足关系:32+42=52,那么围成的三角形是直角三角形.
画画看,如果三角形的三边分别为2.5cm,6cm,6.5cm,它们满足关系“2.52+62=6.52”,画出的三角形是直角三角形吗?换成三边分别为4cm,7.5cm,8.5cm,再试一试.
由上面的几个例子,我们猜想:如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
命题1 如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么 a2+b2=c2.
命题2 如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
命题1、命题2的题设、结论分别是什么?
我们看到,命题2与命题1的题设、结论正好相反.我们把像这样的两个命题叫做互逆命题.
如果把其中一个叫做原命题,那么另一个叫做它的逆命题.例如,如果把命题1当成原命题,那么命题2是原命题1的逆命题.
【针对练习】说出下列命题的逆命题,并判断它们是否正确.
1.原命题:同位角相等,两直线平行.( )
逆命题:两直线平行,同位角相等.( )
2.原命题:对顶角相等.( )
逆命题:相等的角是对顶角.( )
3.原命题:线段垂直平分线上的点与这条线段两个端点的距离相等.( )
逆命题:与线段两个端点距离相等的点在这条线段的垂直平分线上.( )
4.原命题:角平分线上的点到角的两边的距离相等.( )
逆命题:角的内部到角的两边的距离相等的点在角的平分线上.( )
在图(1)中,已知△ABC的三边长分别为a,b,c,且满足a2+b2=c2,要证△ABC一定是直角三角形.我们可以先画一个两条直角边长分别为a,b的Rt△A′B′C′如图(2),如果△ABC与Rt△A′B′C′全等,那么△ABC就是一个直角三角形.
已知△ABC,BC=a,AC=b,AB=c,且a2+b2=c2.
求证:△ABC是直角三角形.
证明:作Rt△A′B′C′,使B′C′=a,A′C′=b,∠C′=90°.
根据勾股定理,A′B′2=B′C′2+A′C′2=a2+b2=c2
∴ A′B′=c
在△ABC和△A′B′C′中,
BC=a=B′C′,AC=b=A′C′,AB=c=A′B′
∴ △ABC≌△A′B′C′(SSS)
∴ ∠C=∠C′=90°
即△ABC是直角三角形.
【归纳】勾股定理 如果直角三角形的两条直角边长分别为a,b,斜边长为 c,那么 a2+b2=c2.
勾股定理的逆定理 如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么这个三角形是直角三角形.
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
典例解析
例1 判断由线段a,b,c组成的三角形是不是直角三角形:
(1) a=15,b=8,c=17;(2) a=13,b=14,c=15.
解:(1)∵ 152+82=225+64=289,172=289
∴ 152+82=172,根据勾股定理的逆定理,这个三角形是直角三角形.
(2)∵ 132+142=169+196=365,152=225
∴ 132+142≠152,根据勾股定理,这个三角形不是直角三角形.
【点睛】根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
【归纳】像15,8,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.
常见勾股数:3,4,5;6,8,10;5,12,13;8,15,17;7,24,25等等.
勾股数拓展性质:一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数. 如:3,4,5;6,8,10;9,12,15;12,16,20…
【针对练习】若△ABC的三边a,b,c满足 a:b: c=3:4:5,是判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
【点睛】已知三角形三边的比例关系判断三角形形状:先设出参数,表示出三条边的长,再用勾股定理的逆定理判断其是否是直角三角形.如果此直角三角形的三边中有两个相同的数,那么该三角形还是等腰三角形.
例2.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴ △ABC是直角三角形.
【针对练习】若△ABC的三边a,b,c,且a+b=4,ab=1,c=,试说明△ABC是直角三角形.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
例3.已知的三条边长分别为,且,,(,是正整数).是直角三角形吗?请证明你的判断.
解:是直角三角形.证明如下:
∵,,(,m,n是正整数),
∴
.
是直角三角形.
【针对练习】已知的三边,,.
求证:是直角三角形.
解:∵的三边,,,
而,,,
∵,
∴,
即,
∴是直角三角形.
例4.已知,,.
(1)在坐标系中描出各点,画出三角形;
(2)求三角形的面积;
(3)仅用无刻度的直尺作出边上的高,并直接写出的长.(保留作图痕迹)
解:(1)如图所示:
(2)
(3)如图所示的线段即所求作的高.
由图可得:
,
∴
∴是直角三角形,
∴
∴
∴
∴
例5.如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.下列各组数中,是勾股数的( )
A.0.3,0.4,0.5 B.9,16,25 C.5,12,13 D.10,15,18
2.下面三角形中是直角三角形的有( )
①三角形三内角之比为1:2:3;
②三角形三内角之比为3:4:5;
③三角形三边之比为1:2:3;
④三角形三边之比为3:4:5.
A.1个 B.2个 C.3个 D.4个
3.下列命题中,逆命题为真命题的是( )
A.全等三角形的对应角相等 B.等角对等边
C.若a=b,则|a|=|b| D.若ac2
A.4 B.3 C.2.5 D.2.4
4.已知一个三角形的三边长分别为2、3、则这个三角形的面积是_____.
5若△ABC的三边a、b、c满足(a-b)(a2+b2-c2)=0,则△ABC是__________________________.
6.命题 “如果a+b=0,那么a=0,b=0” 的逆命题是_______________________,它是____命题.
7.根据下列条件,分别判断以为边的三角形是不是直角三角形.
(1),,.
(2),,.
(3),,.
(4),,(n为正整数)
(5).
8.说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等.
9.已知中,、、所对边长分别为、、, 若、、三边满足,试判断的形状.
10.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,的顶点都在格点上.
(1)求的度数;
(2)求的面积.
【参考答案】
C
B
B
D
3
等腰三角形或直角三角形
如果a=0,b=0,那么a+b=0;真
8.解:(1)∵,,
∴,
∴以为边的三角形不是直角三角形;
(2)∵,,
∴,
∴以为边的三角形是直角三角形;
(3)∵,,
∴,
∴以为边的三角形是直角三角形;
(4)∵,,
∴,
∴以为边的三角形是直角三角形;
(5)∵,
∴设,
∵,,
∴,
∴以为边的三角形是直角三角形.
8.解:(1)逆命题:内错角相等,两条直线平行,此命题成立;
(2)逆命题:如果两个实数的绝对值相等,那么这两个实数相等,此命题不成立;
(3)逆命题:对应角相等的两个三角形是全等三角形,此命题不成立.
9.解:是直角三角形.
理由如下:
,
,,,
,,,
,,
,
是直角三角形.
10.解:(1),
,
,
∵,
∴为直角三角形,
∴,
∵,
∴;
(2).
四、教学反思:
在本课时教学过程中,应以师生共同探讨为主. 激励学生回答问题,激发学生的求知欲.课堂上师生互动频繁,既保证课堂教学进度,又提高课堂学习效率. 学生在探讨过程中也加深了对知识的理解和记忆.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
