17.2.2 勾股定理的逆定理的应用(第二课时)教学设计【2024春人教八下数学同步优质教案】
文档属性
| 名称 | 17.2.2 勾股定理的逆定理的应用(第二课时)教学设计【2024春人教八下数学同步优质教案】 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版初中数学八年级下册
17.2.2 勾股定理的逆定理的应用 教学设计
一、教学目标:
1.灵活应用勾股定理及其逆定理解决实际问题.
2.将实际问题转化成用勾股定理的逆定理解决的数学问题.
二、教学重、难点:
重点:灵活应用勾股定理及其逆定理解决实际问题.
难点:将实际问题转化成用勾股定理的逆定理解决的数学问题.
三、教学过程:
复习回顾
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
∵,a、b为直角边,c为斜边.
∴
勾股定理的逆定理:如果三角形的三边长a、b、c 满足,那么这个三角形是直角三角形.
∵△的三边a、b、c满足
∴是直角三角形
典例解析
例1.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(2)求到的距离.
(1)解:连接,
∵,,,
∴m,
∵,,
∴,
∴是直角三角形,且,
∴四边形花圃的面积
∴四边形花圃的面积是;
(2)过点C作于E,
∵,
∴,
∴,
∴到的距离是.
例2.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路,测得千米,千米,千米.求原来的路线的长.
解:∵千米,千米,千米,即,
∴,
∴是直角三角形,且,
∴,
∴,
设,
∴,
∴,即,
解得:,
答:原来的路线的长为千米.
【针对练习】2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知,,,,技术人员通过测量确定了.
(1)问这片绿地的面积是多少?
(2)小区内部分居民每天必须从点经过点再到点位置,为了方便居民出入,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?
(1)解:如图,连接,
,,,
,
,,
,
是直角三角形,即,
,,
,
(2)解:.
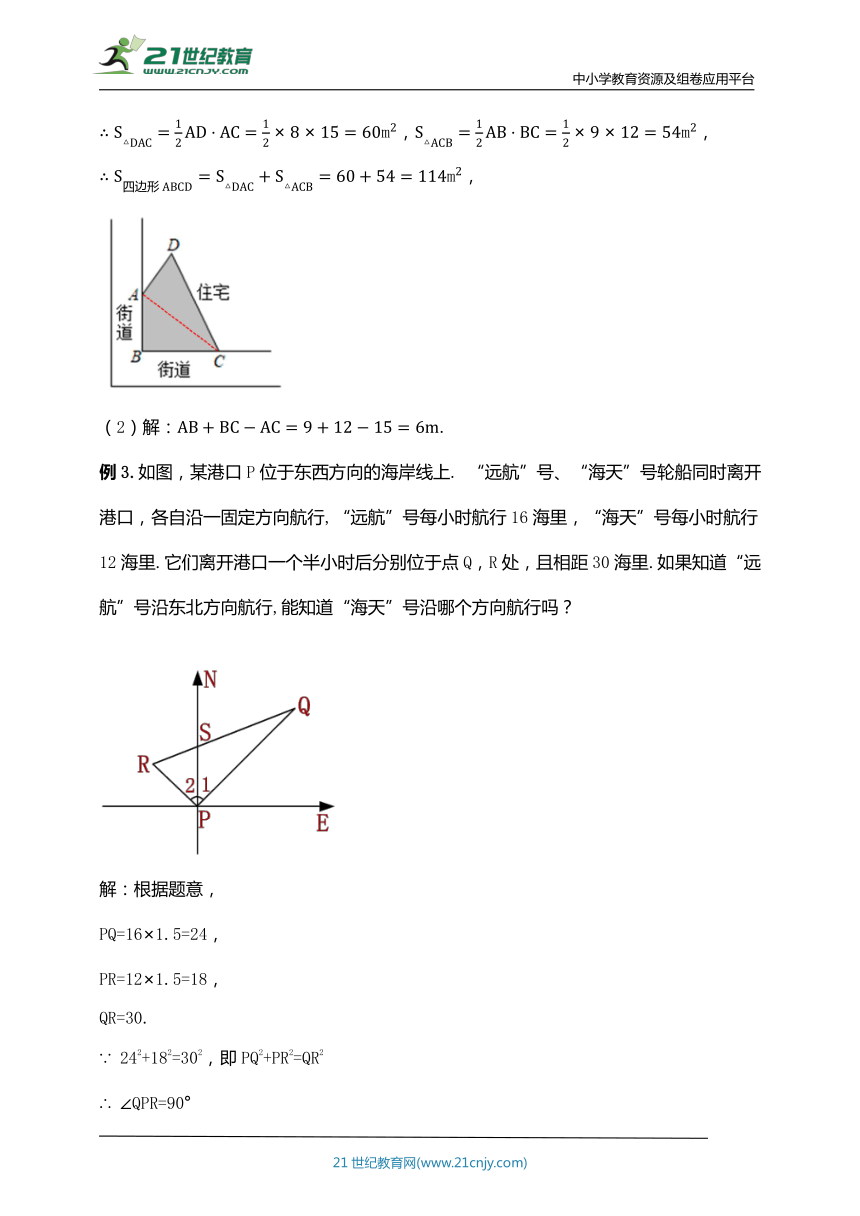
例3.如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
∵ 242+182=302,即PQ2+PR2=QR2
∴ ∠QPR=90°
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.
【点睛】解决实际问题的步骤:构建几何模型(从整体到局部);标注有用信息,明确已知和所求;应用数学知识求解.
【针对练习】如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
分析:根据勾股定理的逆定理得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三角形面积公式有
BC·AB=AC·BD,
即6×8=10BD,解得BD=.
在Rt△BCD中,
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
例4.如图,已知等腰△ABC的底边BC=2cm,AH平分∠BAC交BC于H,D是腰AC上点,且CD=2cm,BD=6cm,求AH的长.
解:∵BC=2,BD=6,CD=2,
∴,,
∴,
∴△BDC为直角三角形,
∴∠BDC=∠ADB=90°,
∵△ABC是等腰三角形,
∴AB=AC,
设AD=x,则AB=AC=x+2,
在Rt△ABD中,勾股定理得,
解得x=8,
∴AB=8+2=10,
∵AB=AC,AH⊥BC,BC=2,
∴BH=HC=,
由勾股定理得AH==3 (cm).
例5.如图所示,在中,,且的周长为,点P从点A开始沿边向B点以每秒的速度移动;点Q从点B沿边向点C以每秒的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
解:设为,为,为,
∵的周长为,
∴,
即,
解得:,
∴,,,
∵,
∴是直角三角形,且.
经过3秒时,,,
又∵在中,,
∴,
即经过3秒时,P、Q两点间的距离为.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
2.如图,在Rt△ABC中,AB=8,AC=6,BC=10,D是AB的中点,P,Q分别是BC,DC上的动点,则AQ+QP的最小值是________.
3.已知:如图,四边形ABCD中,AB=20,BC=15, CD=7,AD=24,∠B=90°.求证:∠A+∠C=180.
4.如图,有一块地,已知∠ADC=90°,AD=4m, CD=3m,AB=13m,BC=12m.求这块地的面积.
5.如图,A,B,C,D是四个小镇,它们之间除(B,C外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A B:10元; A C:12. 5元; A D:8元; B D: 6元;C D:4.5元.为了B,C之间的交通方便,在B,C之间建成笔直的公路,请按上述标准计算出B,C之间的公路的票价为多少元
6.某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离,以沙尘暴中心为圆心,周围以内都会受到沙尘暴影响.
(1)通过计算说明城镇C是否会受到影响;
(2)若沙尘暴中心的移动速度为,则沙尘暴影响该城镇持续的时间有多长?
【参考答案】
C
4.8
3.证明:连接AC.
在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=202+152=252
∴AC=25
∵72+242=252
即CD2+AD2=AC2
∴∠D=90°
∴∠DAB+∠BCD=360°-∠B-∠D=180°
4.解:连接AC.
在Rt△ACD中,根据勾股定理,
AC2=AD2+CD2=42+32=25
∴AC=5m
∵52+122=132
即AC2+BC2=AB2
∴∠ACB=90°
∴S阴=S△ABC-S△ACD=×5×12-×3×4=24(m2)
5.解:连接BC.
∵82+62=102,即AD2+BD2=AB2
∴∠ADB=90°,∴∠BDC=90
在Rt△BDC中,根据勾股定理,BC== =7.5
因此,B,C之间的公路的票价为7.5元.
6.(1)解:作于D,
在三角形中,,
∴是直角三角形,即,
,
,
解得∶千米,
所以,城镇C会受到影响.
(2)解:设沙尘暴中心到点E处城镇C开始受到影响,此时千米,
到F处结束影响,此时千米,
,
千米,
受影响的时间为(小时)
四、教学反思:
本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版初中数学八年级下册
17.2.2 勾股定理的逆定理的应用 教学设计
一、教学目标:
1.灵活应用勾股定理及其逆定理解决实际问题.
2.将实际问题转化成用勾股定理的逆定理解决的数学问题.
二、教学重、难点:
重点:灵活应用勾股定理及其逆定理解决实际问题.
难点:将实际问题转化成用勾股定理的逆定理解决的数学问题.
三、教学过程:
复习回顾
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
∵,a、b为直角边,c为斜边.
∴
勾股定理的逆定理:如果三角形的三边长a、b、c 满足,那么这个三角形是直角三角形.
∵△的三边a、b、c满足
∴是直角三角形
典例解析
例1.如图,一块四边形花圃中,已知,,,,.
(1)求四边形花圃的面积;
(2)求到的距离.
(1)解:连接,
∵,,,
∴m,
∵,,
∴,
∴是直角三角形,且,
∴四边形花圃的面积
∴四边形花圃的面积是;
(2)过点C作于E,
∵,
∴,
∴,
∴到的距离是.
例2.在一条东西走向的河流一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路,测得千米,千米,千米.求原来的路线的长.
解:∵千米,千米,千米,即,
∴,
∴是直角三角形,且,
∴,
∴,
设,
∴,
∴,即,
解得:,
答:原来的路线的长为千米.
【针对练习】2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知,,,,技术人员通过测量确定了.
(1)问这片绿地的面积是多少?
(2)小区内部分居民每天必须从点经过点再到点位置,为了方便居民出入,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?
(1)解:如图,连接,
,,,
,
,,
,
是直角三角形,即,
,,
,
(2)解:.
例3.如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
∵ 242+182=302,即PQ2+PR2=QR2
∴ ∠QPR=90°
由“远航”号沿东北方向航行可知,∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.
【点睛】解决实际问题的步骤:构建几何模型(从整体到局部);标注有用信息,明确已知和所求;应用数学知识求解.
【针对练习】如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
分析:根据勾股定理的逆定理得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三角形面积公式有
BC·AB=AC·BD,
即6×8=10BD,解得BD=.
在Rt△BCD中,
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
例4.如图,已知等腰△ABC的底边BC=2cm,AH平分∠BAC交BC于H,D是腰AC上点,且CD=2cm,BD=6cm,求AH的长.
解:∵BC=2,BD=6,CD=2,
∴,,
∴,
∴△BDC为直角三角形,
∴∠BDC=∠ADB=90°,
∵△ABC是等腰三角形,
∴AB=AC,
设AD=x,则AB=AC=x+2,
在Rt△ABD中,勾股定理得,
解得x=8,
∴AB=8+2=10,
∵AB=AC,AH⊥BC,BC=2,
∴BH=HC=,
由勾股定理得AH==3 (cm).
例5.如图所示,在中,,且的周长为,点P从点A开始沿边向B点以每秒的速度移动;点Q从点B沿边向点C以每秒的速度移动,如果P、Q两点同时出发,经过3秒时,P、Q两点间的距离为多少?
解:设为,为,为,
∵的周长为,
∴,
即,
解得:,
∴,,,
∵,
∴是直角三角形,且.
经过3秒时,,,
又∵在中,,
∴,
即经过3秒时,P、Q两点间的距离为.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。
达标检测
1.在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
2.如图,在Rt△ABC中,AB=8,AC=6,BC=10,D是AB的中点,P,Q分别是BC,DC上的动点,则AQ+QP的最小值是________.
3.已知:如图,四边形ABCD中,AB=20,BC=15, CD=7,AD=24,∠B=90°.求证:∠A+∠C=180.
4.如图,有一块地,已知∠ADC=90°,AD=4m, CD=3m,AB=13m,BC=12m.求这块地的面积.
5.如图,A,B,C,D是四个小镇,它们之间除(B,C外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A B:10元; A C:12. 5元; A D:8元; B D: 6元;C D:4.5元.为了B,C之间的交通方便,在B,C之间建成笔直的公路,请按上述标准计算出B,C之间的公路的票价为多少元
6.某气象局监测到一个沙尘暴中心沿东西方向有A向B移动,已知点C处为以城镇,且点C与A、B两点的距离,以沙尘暴中心为圆心,周围以内都会受到沙尘暴影响.
(1)通过计算说明城镇C是否会受到影响;
(2)若沙尘暴中心的移动速度为,则沙尘暴影响该城镇持续的时间有多长?
【参考答案】
C
4.8
3.证明:连接AC.
在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=202+152=252
∴AC=25
∵72+242=252
即CD2+AD2=AC2
∴∠D=90°
∴∠DAB+∠BCD=360°-∠B-∠D=180°
4.解:连接AC.
在Rt△ACD中,根据勾股定理,
AC2=AD2+CD2=42+32=25
∴AC=5m
∵52+122=132
即AC2+BC2=AB2
∴∠ACB=90°
∴S阴=S△ABC-S△ACD=×5×12-×3×4=24(m2)
5.解:连接BC.
∵82+62=102,即AD2+BD2=AB2
∴∠ADB=90°,∴∠BDC=90
在Rt△BDC中,根据勾股定理,BC== =7.5
因此,B,C之间的公路的票价为7.5元.
6.(1)解:作于D,
在三角形中,,
∴是直角三角形,即,
,
,
解得∶千米,
所以,城镇C会受到影响.
(2)解:设沙尘暴中心到点E处城镇C开始受到影响,此时千米,
到F处结束影响,此时千米,
,
千米,
受影响的时间为(小时)
四、教学反思:
本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
