1.4 整式的乘法第3课时课件(共20张PPT)
文档属性
| 名称 | 1.4 整式的乘法第3课时课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 627.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第3课时
北师大版 数学 七年级下册
4 整式的乘法
第一章 整式的乘除
学习目标
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.(难点)
一、导入新课
复习回顾
2.单项式乘多项式:
单项式与多项式相乘,就是根据分配律用单项式去乘 ,再把所得的 相加.
多项式的每一项
积
1.单项式乘单项式:
单项式与单项式相乘,把它们的 、 分别相乘,其余字母连同它的指数不变,作为积的 .
系数
相同字母的幂
因式
一、导入新课
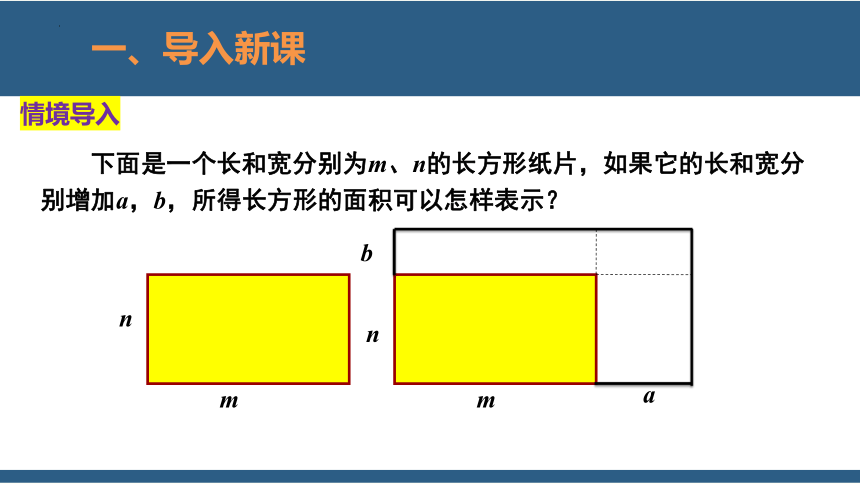
情境导入
下面是一个长和宽分别为m、n的长方形纸片,如果它的长和宽分别增加a,b,所得长方形的面积可以怎样表示?
m
n
n
m
b
a
二、新知探究
探究:多项式乘多项式
n
m
b
a
长方形的面积可以有4种表示方式:(m+a)(n+b),n(m+a)+b(m+a),m(n+b)+a(n+b),mn+mb+an+ab.
从而:(m+a)(n+b)=n(m+a)+b(m+a)
=m(n+b)+a(n+b)=mn+mb+an+ab.
你认为他的想法对吗?从中你受到了什么启发?
二、新知探究
把(m+a)或者(n+b) 看成一个整体,利用乘法分配律,可以得到(m+a)(n+b)=(m+a)n+(m+a)b=mn+mb+an+ab,或(m+a)(n+b)=m(n+b)+a(n+b)=mn+mb+an+ab.
议一议:你是用什么方法计算上面的问题的?
如何进行多项式与多项式相乘的运算?
二、新知探究
知识归纳
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘多项式法则
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,乘后结果要相加,化简、排列才算完.
二、新知探究
1.计算:(1)(1-x)(0.6-x); (2)(2x+y)(x-y);
解: (1) 原式=1×0.6-1×x-x·0.6+x·x
=0.6-x-0.6x+x2
=0.6-1.6x+x2;
(2) 原式=2x·x-2x·y+y·x-y·y
=2x2-2xy+xy-y2
=2x2-xy-y2;
跟踪练习
两项相乘时,先定符号,最后的结果要合并同类项.
二、新知探究
解:原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
(3) (x+y)(x2-xy+y2).
注意:(1)不要漏乘;
(2)注意符号问题;
(3)最后结果应化成最简形式(是同类项的要合并).
二、新知探究
2.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
跟踪练习
三、典例精析
例1 计算:(1)(-2m-1)(3m-2); (2)(x-y)2.
解:(1)原式=-2m·3m-2m·(-2)-1·3m-1×(-2)
=-6m2+4m-3m+2
=-6m2+m+2.
(2)原式=(x-y)(x-y)
=x2-xy-xy+y2
=x2-2xy+y2.
三、典例精析
例2:若(x-2)(x2+ax+b)的积中不含x的二次项和一次项,则a,b的值分别是多少
解:(x-2)(x2+ax+b)
=x3+ax2+bx-2x2-2ax-2b
=x3+(a-2)x2+(b-2a)x-2b.
因为(x-2)(x2+ax+b)的积中不含x的二次项和一次项,
所以a-2=0,b-2a=0,
解得a=2,b=4.
四、当堂练习
1.计算(a-2)(a+3)的结果是( )
A.a2-6 B.a2+a-6
C.a2+6 D.a2-a+6
B
2.下列各式中,错误的是 ( )
A.(x+1)(x+2)=x2+3x+2
B.(x-4)(x+4)=x2-16
C.(2x+3)(2x-6)=2x2-3x-18
D.(2x-1)(2x+2)=4x2+2x-2
C
4.设M=(x-3)(x-7),N=(x-2)(x-8),则M,N的大小关系为 ( )
A.M>N B.M=N C.M四、当堂练习
3.若(x+5)(2x-3)=2x2+mx-15,则 ( )
A.m=7 B.m=-3 C.m=-7 D.m=10
A
A
5.如果长方形的长为(4a2-2a+1),宽为(2a+1),那么这个长方形的面积为( )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
D
6.若(x+q)与()的乘积中不含x的一次项,则q的值是( )A. B.5 C.-5 D.-
7.如图所示,甲、乙、丙、丁四位同学各给出了一种表示该大长方形面积的式子:①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);
④2am+2an+bm+bn.其中正确的是( )
A.①② B.③④
C.①②③ D.①②③④
四、当堂练习
D
D
10.如图所示,为了扩大街心花园的绿地面积,把一块原长a m、宽m m的长方形绿地,增长了b m,加宽了n m,则扩大后的绿地的面积是 m2.
8.若a2+a=1,则(a-5)(a+6)= .
四、当堂练习
-29
(am+bm+an+bn)
四、当堂练习
11.计算:(1)(3x+2)(x+2); (2)(3x-2y)(3x+2y);
(3)(4y-1)(5-y); (4)(3a-2)2.
解:(1)原式=3x2+6x+2x+4=3x2+8x+4.
(2)(3x-2y)(3x+2y)=9x2+6xy-6xy-4y2=9x2-4y2.
(3)原式=20y-4y2-5+y=-4y2+21y-5.
(4)(3a-2)2=(3a-2)(3a-2)=9a2-6a-6a+4=9a2-12a+4.
四、当堂练习
12.已知A=1+2x,B=1-2x+4x2,C=1-4x3.
(1)计算:A·B-C;
(2)当x=-1时,求A·B-C的值.
解:(1)因为A=1+2x,B=1-2x+4x2,C=1-4x3,
所以A·B-C=(1+2x)(1-2x+4x2)-(1-4x3)
=1-2x+4x2+2x-4x2+8x3-1+ 4x3=12x3.
(2)当x=-1时,A·B-C=12x3=12×(-1)3=-12.
五、课堂小结
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
多项式乘多项式
运算法则
注意
实质上是转化为单项式×多项式的运算
不要漏乘;
正确确定各项符号;
结果要最简.
六、作业布置
习题1.8
第3课时
北师大版 数学 七年级下册
4 整式的乘法
第一章 整式的乘除
学习目标
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.(难点)
一、导入新课
复习回顾
2.单项式乘多项式:
单项式与多项式相乘,就是根据分配律用单项式去乘 ,再把所得的 相加.
多项式的每一项
积
1.单项式乘单项式:
单项式与单项式相乘,把它们的 、 分别相乘,其余字母连同它的指数不变,作为积的 .
系数
相同字母的幂
因式
一、导入新课
情境导入
下面是一个长和宽分别为m、n的长方形纸片,如果它的长和宽分别增加a,b,所得长方形的面积可以怎样表示?
m
n
n
m
b
a
二、新知探究
探究:多项式乘多项式
n
m
b
a
长方形的面积可以有4种表示方式:(m+a)(n+b),n(m+a)+b(m+a),m(n+b)+a(n+b),mn+mb+an+ab.
从而:(m+a)(n+b)=n(m+a)+b(m+a)
=m(n+b)+a(n+b)=mn+mb+an+ab.
你认为他的想法对吗?从中你受到了什么启发?
二、新知探究
把(m+a)或者(n+b) 看成一个整体,利用乘法分配律,可以得到(m+a)(n+b)=(m+a)n+(m+a)b=mn+mb+an+ab,或(m+a)(n+b)=m(n+b)+a(n+b)=mn+mb+an+ab.
议一议:你是用什么方法计算上面的问题的?
如何进行多项式与多项式相乘的运算?
二、新知探究
知识归纳
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘多项式法则
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,乘后结果要相加,化简、排列才算完.
二、新知探究
1.计算:(1)(1-x)(0.6-x); (2)(2x+y)(x-y);
解: (1) 原式=1×0.6-1×x-x·0.6+x·x
=0.6-x-0.6x+x2
=0.6-1.6x+x2;
(2) 原式=2x·x-2x·y+y·x-y·y
=2x2-2xy+xy-y2
=2x2-xy-y2;
跟踪练习
两项相乘时,先定符号,最后的结果要合并同类项.
二、新知探究
解:原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
(3) (x+y)(x2-xy+y2).
注意:(1)不要漏乘;
(2)注意符号问题;
(3)最后结果应化成最简形式(是同类项的要合并).
二、新知探究
2.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
跟踪练习
三、典例精析
例1 计算:(1)(-2m-1)(3m-2); (2)(x-y)2.
解:(1)原式=-2m·3m-2m·(-2)-1·3m-1×(-2)
=-6m2+4m-3m+2
=-6m2+m+2.
(2)原式=(x-y)(x-y)
=x2-xy-xy+y2
=x2-2xy+y2.
三、典例精析
例2:若(x-2)(x2+ax+b)的积中不含x的二次项和一次项,则a,b的值分别是多少
解:(x-2)(x2+ax+b)
=x3+ax2+bx-2x2-2ax-2b
=x3+(a-2)x2+(b-2a)x-2b.
因为(x-2)(x2+ax+b)的积中不含x的二次项和一次项,
所以a-2=0,b-2a=0,
解得a=2,b=4.
四、当堂练习
1.计算(a-2)(a+3)的结果是( )
A.a2-6 B.a2+a-6
C.a2+6 D.a2-a+6
B
2.下列各式中,错误的是 ( )
A.(x+1)(x+2)=x2+3x+2
B.(x-4)(x+4)=x2-16
C.(2x+3)(2x-6)=2x2-3x-18
D.(2x-1)(2x+2)=4x2+2x-2
C
4.设M=(x-3)(x-7),N=(x-2)(x-8),则M,N的大小关系为 ( )
A.M>N B.M=N C.M
3.若(x+5)(2x-3)=2x2+mx-15,则 ( )
A.m=7 B.m=-3 C.m=-7 D.m=10
A
A
5.如果长方形的长为(4a2-2a+1),宽为(2a+1),那么这个长方形的面积为( )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
D
6.若(x+q)与()的乘积中不含x的一次项,则q的值是( )A. B.5 C.-5 D.-
7.如图所示,甲、乙、丙、丁四位同学各给出了一种表示该大长方形面积的式子:①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);
④2am+2an+bm+bn.其中正确的是( )
A.①② B.③④
C.①②③ D.①②③④
四、当堂练习
D
D
10.如图所示,为了扩大街心花园的绿地面积,把一块原长a m、宽m m的长方形绿地,增长了b m,加宽了n m,则扩大后的绿地的面积是 m2.
8.若a2+a=1,则(a-5)(a+6)= .
四、当堂练习
-29
(am+bm+an+bn)
四、当堂练习
11.计算:(1)(3x+2)(x+2); (2)(3x-2y)(3x+2y);
(3)(4y-1)(5-y); (4)(3a-2)2.
解:(1)原式=3x2+6x+2x+4=3x2+8x+4.
(2)(3x-2y)(3x+2y)=9x2+6xy-6xy-4y2=9x2-4y2.
(3)原式=20y-4y2-5+y=-4y2+21y-5.
(4)(3a-2)2=(3a-2)(3a-2)=9a2-6a-6a+4=9a2-12a+4.
四、当堂练习
12.已知A=1+2x,B=1-2x+4x2,C=1-4x3.
(1)计算:A·B-C;
(2)当x=-1时,求A·B-C的值.
解:(1)因为A=1+2x,B=1-2x+4x2,C=1-4x3,
所以A·B-C=(1+2x)(1-2x+4x2)-(1-4x3)
=1-2x+4x2+2x-4x2+8x3-1+ 4x3=12x3.
(2)当x=-1时,A·B-C=12x3=12×(-1)3=-12.
五、课堂小结
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
多项式乘多项式
运算法则
注意
实质上是转化为单项式×多项式的运算
不要漏乘;
正确确定各项符号;
结果要最简.
六、作业布置
习题1.8
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
