1.5.1 平方差公式课件(共24张PPT)
文档属性
| 名称 | 1.5.1 平方差公式课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 709.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
新课标 北师大版
七年级下册
1.5.1平方差公式(第1课时)
第一章
整式的乘除
学习目标
1.掌握平方差公式,能正确利用公式进行计算.
2.通过从多项式的乘法到乘法公式,再运用公式计算多项式的乘法,培养从一般到特殊,再从特殊到一般的思维能力.
新课引入
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
即(a+b)(m+n)=am+an+bm+bn.
新课引入
王敏同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王敏就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你好像是个神童,怎么算得这么快?”
王敏同学说:“过奖了,我利用了在数学上刚学过的一个公式.”
你知道王敏同学用的是一个什么样的公式吗?
核心知识点一
探究学方差公式
计算下列各题:
(1)(2n+1)(n-3) (2)(x+y)(x-3y)
(3)(x+2)(x-2) (4)(1+3a)(1-3a)
(5)(x+5y)(x-5y) (6)(2y-z)(2y-z)
=2n2-5n-3
=x2-2xy-3y2
=x2-4
=1-9a2
=x2-25y2
=4y2-z2
观察后面四个算式及其结果,你有什么发现吗?
两数和与这两数差的积,等于这两数的平方的差.
平方差公式:
(a+b)(a-b)= .
平方差
a2-b2
文字语言:两个数的和与这两个数的差的积,等于
这两个数的 .
用自己的语言叙述这个式子.
如何推导这个式子呢?
(b+a)( b+a )=a2 b2
(a–b) (a+b) =a2 b2
公式变形:
( a+b)(a b )
= a2 b2.
1.代数证明
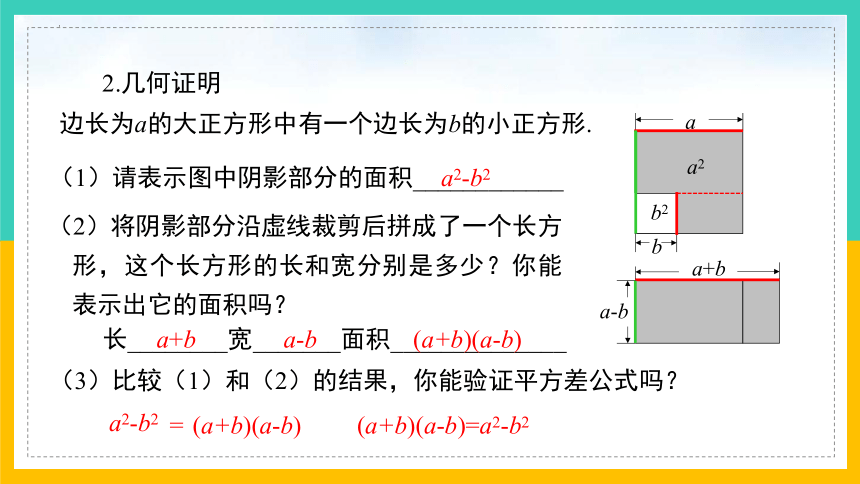
2.几何证明
边长为a的大正方形中有一个边长为b的小正方形.
(2)将阴影部分沿虚线裁剪后拼成了一个长方形,这个长方形的长和宽分别是多少?你能表示出它的面积吗?
a
b
(1)请表示图中阴影部分的面积____________
(3)比较(1)和(2)的结果,你能验证平方差公式吗?
a2-b2
a+b
a-b
长________宽_______面积______________
a+b
a-b
(a+b)(a-b)
a2-b2
(a+b)(a-b)=a2-b2
(a+b)(a-b)
=
a2
b2
寻找a,b,试着完成表格,加深对公式的认识
(a+b)(a-b) a b a -b 最后结果
(5+6x)(5 6x)
(-x+1)(-x-1)
5
6x
5 -(6x)
25-36x
1
-x
(-x) -1
x -1
相同项
相反项
初 识 平 方 差 公 式
(a+b)(a b)=a2 b2
结构特点: (1) 公式左边两个二项式必须是
相同两数的和与差相乘;
且左边两括号内的第一项相等、
第二项符号相反
[互为相反数(式)];
(2) 公式右边是这两个数的平方差;
即右边是左边括号内的第一项的平方减去第二项的平方.
(3) 公式中的 a和b 可以代表数,也可以是代数式.
练一练:口答下列各题:
(l)(-a+b)(a+b)=_________.
(2)(a-b)(b+a)= __________.
(3)(-a-b)(-a+b)= ________.
(4)(a-b)(-a-b)= _________.
a2-b2
a2-b2
b2-a2
b2-a2
例1 利用平方差公式计算:
------- 与y的和与差的积
-------利用平方差公式得 与y的平方差
-------整理出最后结果
(1)
(2)(ab+8)(ab-8)
-----利用平方差公式得ab与8的平方差
------整理出最后结果
------ab与8的和与差的积
例2 利用平方差公式计算:
解:
(1)(5+6x)(5-6x) (2)(x-2y)(x+2y) (3)(-m+n)(-m-n)
(1)(5+6x)(5-6x)
=52-(6x)2
=25-36x2
(2)(x-2y)(x+2y)
=x2-(2y)2
=x2-4y2
(3)(-m+n)(-m-n)
=(-m)2-n2
=m2-n2
例3 下列各式能否用平方差公式计算 若能,请算出结果;若不能,说明理由.
(1) (-a+b)(a+b)
(2)(a-b)(-a-b)
(3)(-b+a)(a-b)
(4)(-b-a)(b-a)
(5)(a+b)(-a-b)
=(b-a)(b+a)=b2-a2
=(-b+a)(-b-a)=(-b)2-a2 =b2-a2
×
×
=(-a-b)(-a+b)=(-a)2-b2 =a2-b2
注意事项:
1. 不要漏括号.
2. 确定相同项和相反项.
随堂练习
1. 若a2-b2=- ,a+b=- ,则a-b的值为( )
2. 用平方差公式计算(x-1)(x+1)(x2+1),结果正确的是( )
A. x4-1 B. x4+1 C.(x-1)4 D.(x+1)4
A
A
3. 下列式子不能用平方差公式计算的是( )
A. (m+n)(m-n) B. (m-n)(-m-n)
C. (m-n)(-m+n) D. (n-m)(-m-n)
4. 下列各式计算正确的是( )
A. 2a2+3a2=5a4 B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2 D. a3·(-2a)=-2a3
C
C
5. 用(a+b)(a-b)=a2-b2的公式计算(x+2y-1)·(x-2y+1)时,下列变形正确的是( )
A. [x-(2y+1)]2 B. [x+(2y+1)]2
C. [x-(2y-1)][x+(2y-1)] D. [(x-2y)+1][(x-2y)-1]
6. (a+3b)(a-3b)的计算结果是( )
A. a2-6b2 B. a2-9b2
C. a2-6ab+9b2 D. a2+6ab+9b2
C
B
7. 计算:
(1)(x+6)(x-6)=________;
(2)(2+a)(2-a)=________ ;
(3)(x+2y)(x-2y)=________ ;
(4)(2m-5n)(2m+5n)=________.
4m2-25n2
x2-36
4-a2
x2-4y2
8. 计算:
(1) (-2xy+3y)(-2xy-3y);
(2) (2x-y)(y+2x)-(2y+x)(2y-x);
解:原式=4x2y2-9y2.
解:原式=4x2-y2-4y2+x2
=5x2-5y2.
9.化简:3(2a+1)(2a-1)-4a(a-2).
解:原式=3(4a2-1)-4a2+8a
=12a2-3-4a2+8a
=8a2+8a-3.
10.先化简,再求值:2(3x+1)(1-3x)+(x-2)(2+x),其中x=2.
解:2(3x+1)(1-3x)+(x-2)(2+x)
=2(1+3x)(1-3x)+(x-2)(x+2)
=2(1-9x2)+(x2-4)
=2-18x2+x2-4
=-17x2-2.
当x=2时,原式=-17×22-2=-17×4-2=-70.
课堂小结
谢谢聆听
新课标 北师大版
七年级下册
1.5.1平方差公式(第1课时)
第一章
整式的乘除
学习目标
1.掌握平方差公式,能正确利用公式进行计算.
2.通过从多项式的乘法到乘法公式,再运用公式计算多项式的乘法,培养从一般到特殊,再从特殊到一般的思维能力.
新课引入
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
即(a+b)(m+n)=am+an+bm+bn.
新课引入
王敏同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王敏就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你好像是个神童,怎么算得这么快?”
王敏同学说:“过奖了,我利用了在数学上刚学过的一个公式.”
你知道王敏同学用的是一个什么样的公式吗?
核心知识点一
探究学方差公式
计算下列各题:
(1)(2n+1)(n-3) (2)(x+y)(x-3y)
(3)(x+2)(x-2) (4)(1+3a)(1-3a)
(5)(x+5y)(x-5y) (6)(2y-z)(2y-z)
=2n2-5n-3
=x2-2xy-3y2
=x2-4
=1-9a2
=x2-25y2
=4y2-z2
观察后面四个算式及其结果,你有什么发现吗?
两数和与这两数差的积,等于这两数的平方的差.
平方差公式:
(a+b)(a-b)= .
平方差
a2-b2
文字语言:两个数的和与这两个数的差的积,等于
这两个数的 .
用自己的语言叙述这个式子.
如何推导这个式子呢?
(b+a)( b+a )=a2 b2
(a–b) (a+b) =a2 b2
公式变形:
( a+b)(a b )
= a2 b2.
1.代数证明
2.几何证明
边长为a的大正方形中有一个边长为b的小正方形.
(2)将阴影部分沿虚线裁剪后拼成了一个长方形,这个长方形的长和宽分别是多少?你能表示出它的面积吗?
a
b
(1)请表示图中阴影部分的面积____________
(3)比较(1)和(2)的结果,你能验证平方差公式吗?
a2-b2
a+b
a-b
长________宽_______面积______________
a+b
a-b
(a+b)(a-b)
a2-b2
(a+b)(a-b)=a2-b2
(a+b)(a-b)
=
a2
b2
寻找a,b,试着完成表格,加深对公式的认识
(a+b)(a-b) a b a -b 最后结果
(5+6x)(5 6x)
(-x+1)(-x-1)
5
6x
5 -(6x)
25-36x
1
-x
(-x) -1
x -1
相同项
相反项
初 识 平 方 差 公 式
(a+b)(a b)=a2 b2
结构特点: (1) 公式左边两个二项式必须是
相同两数的和与差相乘;
且左边两括号内的第一项相等、
第二项符号相反
[互为相反数(式)];
(2) 公式右边是这两个数的平方差;
即右边是左边括号内的第一项的平方减去第二项的平方.
(3) 公式中的 a和b 可以代表数,也可以是代数式.
练一练:口答下列各题:
(l)(-a+b)(a+b)=_________.
(2)(a-b)(b+a)= __________.
(3)(-a-b)(-a+b)= ________.
(4)(a-b)(-a-b)= _________.
a2-b2
a2-b2
b2-a2
b2-a2
例1 利用平方差公式计算:
------- 与y的和与差的积
-------利用平方差公式得 与y的平方差
-------整理出最后结果
(1)
(2)(ab+8)(ab-8)
-----利用平方差公式得ab与8的平方差
------整理出最后结果
------ab与8的和与差的积
例2 利用平方差公式计算:
解:
(1)(5+6x)(5-6x) (2)(x-2y)(x+2y) (3)(-m+n)(-m-n)
(1)(5+6x)(5-6x)
=52-(6x)2
=25-36x2
(2)(x-2y)(x+2y)
=x2-(2y)2
=x2-4y2
(3)(-m+n)(-m-n)
=(-m)2-n2
=m2-n2
例3 下列各式能否用平方差公式计算 若能,请算出结果;若不能,说明理由.
(1) (-a+b)(a+b)
(2)(a-b)(-a-b)
(3)(-b+a)(a-b)
(4)(-b-a)(b-a)
(5)(a+b)(-a-b)
=(b-a)(b+a)=b2-a2
=(-b+a)(-b-a)=(-b)2-a2 =b2-a2
×
×
=(-a-b)(-a+b)=(-a)2-b2 =a2-b2
注意事项:
1. 不要漏括号.
2. 确定相同项和相反项.
随堂练习
1. 若a2-b2=- ,a+b=- ,则a-b的值为( )
2. 用平方差公式计算(x-1)(x+1)(x2+1),结果正确的是( )
A. x4-1 B. x4+1 C.(x-1)4 D.(x+1)4
A
A
3. 下列式子不能用平方差公式计算的是( )
A. (m+n)(m-n) B. (m-n)(-m-n)
C. (m-n)(-m+n) D. (n-m)(-m-n)
4. 下列各式计算正确的是( )
A. 2a2+3a2=5a4 B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2 D. a3·(-2a)=-2a3
C
C
5. 用(a+b)(a-b)=a2-b2的公式计算(x+2y-1)·(x-2y+1)时,下列变形正确的是( )
A. [x-(2y+1)]2 B. [x+(2y+1)]2
C. [x-(2y-1)][x+(2y-1)] D. [(x-2y)+1][(x-2y)-1]
6. (a+3b)(a-3b)的计算结果是( )
A. a2-6b2 B. a2-9b2
C. a2-6ab+9b2 D. a2+6ab+9b2
C
B
7. 计算:
(1)(x+6)(x-6)=________;
(2)(2+a)(2-a)=________ ;
(3)(x+2y)(x-2y)=________ ;
(4)(2m-5n)(2m+5n)=________.
4m2-25n2
x2-36
4-a2
x2-4y2
8. 计算:
(1) (-2xy+3y)(-2xy-3y);
(2) (2x-y)(y+2x)-(2y+x)(2y-x);
解:原式=4x2y2-9y2.
解:原式=4x2-y2-4y2+x2
=5x2-5y2.
9.化简:3(2a+1)(2a-1)-4a(a-2).
解:原式=3(4a2-1)-4a2+8a
=12a2-3-4a2+8a
=8a2+8a-3.
10.先化简,再求值:2(3x+1)(1-3x)+(x-2)(2+x),其中x=2.
解:2(3x+1)(1-3x)+(x-2)(2+x)
=2(1+3x)(1-3x)+(x-2)(x+2)
=2(1-9x2)+(x2-4)
=2-18x2+x2-4
=-17x2-2.
当x=2时,原式=-17×22-2=-17×4-2=-70.
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
