1.4.2 整式的乘法课件(共24张PPT)
文档属性
| 名称 | 1.4.2 整式的乘法课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 779.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
新课标 北师大版
七年级下册
1.4.2整式的乘法(第2课时)
第一章
整式的乘除
学习目标
1.能根据乘法分配律和单项式与单项式相乘的法则,探究单项式与多项式相乘的法则;
2.会用单项式与多项式相乘法则进行乘法运算和简单运用
新课引入
1、单项式乘法的法则:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2、什么叫多项式
几个单项式的和叫做多项式.
在多项式中,每个单项式叫做多项式的项.
新课引入
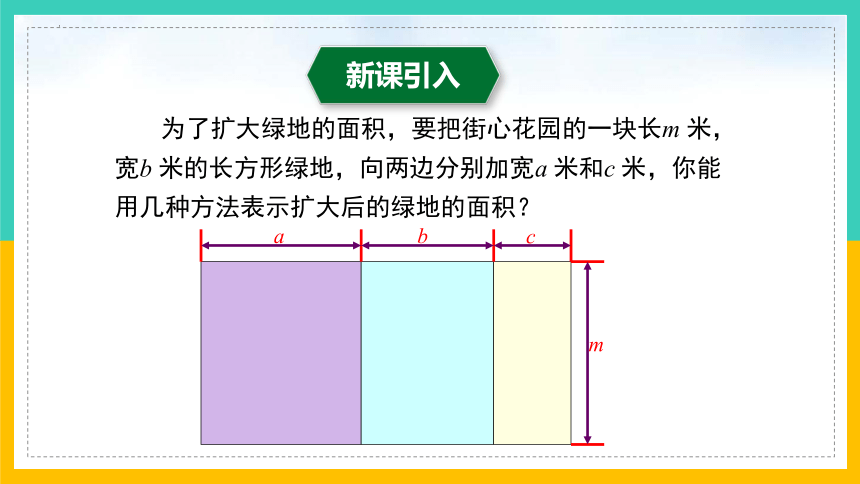
为了扩大绿地的面积,要把街心花园的一块长m 米,宽b 米的长方形绿地,向两边分别加宽a 米和c 米,你能用几种方法表示扩大后的绿地的面积?
c
b
a
m
核心知识点一
探究学习
单项式与多项式相乘
c
b
a
m
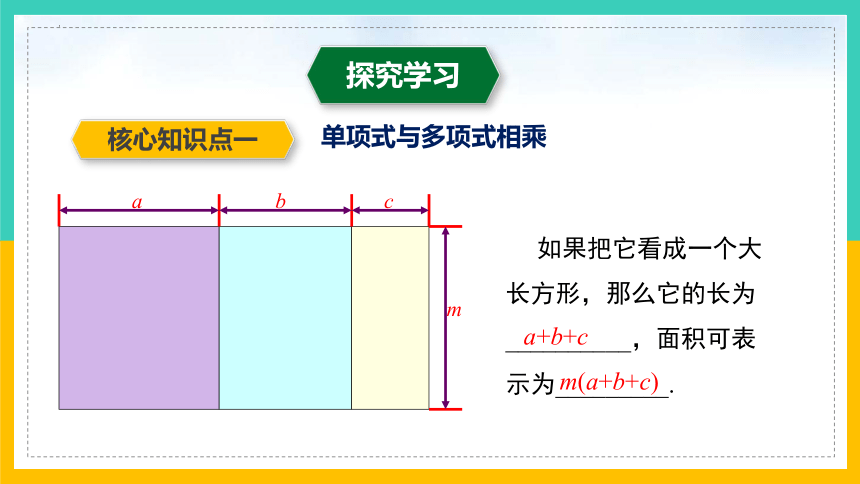
如果把它看成一个大长方形,那么它的长为__________,面积可表示为_________.
a+b+c
m(a+b+c)
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
m
a
m
c
ma
mc
mb
m
b
=
m(a+b+c)
ma+mb+mc
你能用所学的知识解释这个等式吗?
m( a + b + c)=
ma
mb
mc
+
+
2a2(3a2-5b)=
2a2.3a2
2a2.(-5b)
+
=6a4-10a2b
(-2a2)(3ab2-5b)=
(-2a2).3ab2
(-2a2).(-5b)
+
=-6a3b2+10a2b
类似的:
乘法分配律
ab+ac+ad
a(b+c+d)
单项式与多项式相乘,就是根据________,用单项式去乘多项式的_______,再把所得的积_____.
单项式乘多项式的运算法则
分配律
每一项
相加
解:原式
单项式乘以单项式
单项式乘以多项式
转化
单项式乘以多项式
是如何运算?
=2x·x+2x·2y
=2x2+4xy
解:原式
解:原式
+
分配律
单项式乘单项式
+
例1 计算:
练一练:计算:
6x2-2x3
(1)2x(3x-x2)
不要漏项
积的项数与原多项式的项数相同
相乘时,多项式的每一项都包括它前面的符号
单项式系数为负数时,要注意每一项乘积的符号
6a3-6ab+3a
-x2+xy
(1)4(a-b+1)=___________________;
4a-4b+4
(2)3x(2x-y2)=___________________;
6x2-3xy2
(3)(2x-5y+6z)(-3x) =___________________;
-6x2+15xy-18xz
(4)(-2a2)2(-a-2b+c)=___________________.
-4a5-8a4b+4a4c
练一练:计算
例:先化简,再求值:x2(3-x)+x(x2-2x)+1,
其中x=-3.
分析:直接将已知数值代入式子求值运算量大,
一般是先化简,再将数值代入求值.
解:原式=3x2-x3+x3-2x2+1=x2+1,
当x=-3时,原式=(-3)2+1=9+1=10.
a
做一做:计算下图中图形的面积。
法一
法二
法三
t
at+(b-t)t=at+bt-t2
bt+(a-t)t=at+bt-t2
(b+a-t)t=at+bt-t2
ab-(a-t)(b-t)=at+bt-t2
t
a
b
t
t
a
b
t
法四
b-t
a-t
a-t
割补法
b-t
a-t
a
随堂练习
1. 下列计算正确的是( )
A. a2(a3+1)=a6+a2
B. x(x2-x)=x3-x
C. 2x(x-y)=2x2-2xy
D. -3x(x-1)=-3x2-3x
C
2.要使x (x+a )+3x-2b=x 2+5x+4成立,则a,b 的值分别为( )
A.-2,-2 B.2,2
C.2,-2 D.-2,2
C
3.若计算(x 2+ax+5)·(-2x )-6x 2的结果中不含有
x 2项,则a 的值为( )
A.-3 B.- C.0 D.3
A
A
5. 计算:
(1)5x(x+2)=________;
(2)(x-3y)·(-2x)=______________;
(3)(4m2-2mn)· m=______________;
(4)(-2a2)·(3a-5ab+1)= .
-6a3+10a3b-2a2
5x2+10x
-2x2+6xy
2m3-m2n
6. 计算:
(1) 4(a-b+1); (2) 3x(2x-y2)
(3) -3x(2x-5y+6z); (4) (-2a2)(-a-2b+c)
解:(1) 4(a-b+1)
=4a-4b+4;
(2)3x(2x-y2)=3x·2x+3x·(-y2)
=6x2-3xy2;
=2a3+4a2b-2a2c
6. 计算:
(1) 4(a-b+1); (2) 3x(2x-y2)
(3) -3x(2x-5y+6z); (4) (-2a2)(-a-2b+c)
(3)-3x(2x-5y+6z)
=-3x·(2x)+(-3x)·(-5y)+(-3x)·6z
=-6x2+15xy-18xz;
(4)(-2a2)(-a-2b+c)
=(-2a2)·(-a)+(-2a2)·(-2b)+(-2a2)·c
=2a3+4a2b-2a2c
7.化简求值:x2(x-1)-x(x2+x-1),其中,x= .
解:原式=x3-x2-x3-x2+x
=-2x2+x
当x= 时,原式=
8. 化简求值:x(x2-1)+2x2(x+1)-3x(2x-5),其中,x=-1.
解:原式=x3-x+2x3+2x2-6x2+15x
=3x3-4x2+14x
当x=-1时,
原式=3×(-1)3-4×(-1)2+14×(-1)
=-3-4-14
=-21
9.当m,n为何值时, x[x(x+m)+nx(x+1)+m] 的展开式中不含x2项和x3项?
解: x[x(x+m)+nx(x+1)+m]
= x(x2+mx+nx2+nx+m)
= (1+n)x3+ (m+n)x2+ mx,
因为展开式中不含x2项和x3项,
所以1+n=0,m+n=0,
解得n=-1,m=1.
课堂小结
谢谢聆听
新课标 北师大版
七年级下册
1.4.2整式的乘法(第2课时)
第一章
整式的乘除
学习目标
1.能根据乘法分配律和单项式与单项式相乘的法则,探究单项式与多项式相乘的法则;
2.会用单项式与多项式相乘法则进行乘法运算和简单运用
新课引入
1、单项式乘法的法则:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2、什么叫多项式
几个单项式的和叫做多项式.
在多项式中,每个单项式叫做多项式的项.
新课引入
为了扩大绿地的面积,要把街心花园的一块长m 米,宽b 米的长方形绿地,向两边分别加宽a 米和c 米,你能用几种方法表示扩大后的绿地的面积?
c
b
a
m
核心知识点一
探究学习
单项式与多项式相乘
c
b
a
m
如果把它看成一个大长方形,那么它的长为__________,面积可表示为_________.
a+b+c
m(a+b+c)
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
m
a
m
c
ma
mc
mb
m
b
=
m(a+b+c)
ma+mb+mc
你能用所学的知识解释这个等式吗?
m( a + b + c)=
ma
mb
mc
+
+
2a2(3a2-5b)=
2a2.3a2
2a2.(-5b)
+
=6a4-10a2b
(-2a2)(3ab2-5b)=
(-2a2).3ab2
(-2a2).(-5b)
+
=-6a3b2+10a2b
类似的:
乘法分配律
ab+ac+ad
a(b+c+d)
单项式与多项式相乘,就是根据________,用单项式去乘多项式的_______,再把所得的积_____.
单项式乘多项式的运算法则
分配律
每一项
相加
解:原式
单项式乘以单项式
单项式乘以多项式
转化
单项式乘以多项式
是如何运算?
=2x·x+2x·2y
=2x2+4xy
解:原式
解:原式
+
分配律
单项式乘单项式
+
例1 计算:
练一练:计算:
6x2-2x3
(1)2x(3x-x2)
不要漏项
积的项数与原多项式的项数相同
相乘时,多项式的每一项都包括它前面的符号
单项式系数为负数时,要注意每一项乘积的符号
6a3-6ab+3a
-x2+xy
(1)4(a-b+1)=___________________;
4a-4b+4
(2)3x(2x-y2)=___________________;
6x2-3xy2
(3)(2x-5y+6z)(-3x) =___________________;
-6x2+15xy-18xz
(4)(-2a2)2(-a-2b+c)=___________________.
-4a5-8a4b+4a4c
练一练:计算
例:先化简,再求值:x2(3-x)+x(x2-2x)+1,
其中x=-3.
分析:直接将已知数值代入式子求值运算量大,
一般是先化简,再将数值代入求值.
解:原式=3x2-x3+x3-2x2+1=x2+1,
当x=-3时,原式=(-3)2+1=9+1=10.
a
做一做:计算下图中图形的面积。
法一
法二
法三
t
at+(b-t)t=at+bt-t2
bt+(a-t)t=at+bt-t2
(b+a-t)t=at+bt-t2
ab-(a-t)(b-t)=at+bt-t2
t
a
b
t
t
a
b
t
法四
b-t
a-t
a-t
割补法
b-t
a-t
a
随堂练习
1. 下列计算正确的是( )
A. a2(a3+1)=a6+a2
B. x(x2-x)=x3-x
C. 2x(x-y)=2x2-2xy
D. -3x(x-1)=-3x2-3x
C
2.要使x (x+a )+3x-2b=x 2+5x+4成立,则a,b 的值分别为( )
A.-2,-2 B.2,2
C.2,-2 D.-2,2
C
3.若计算(x 2+ax+5)·(-2x )-6x 2的结果中不含有
x 2项,则a 的值为( )
A.-3 B.- C.0 D.3
A
A
5. 计算:
(1)5x(x+2)=________;
(2)(x-3y)·(-2x)=______________;
(3)(4m2-2mn)· m=______________;
(4)(-2a2)·(3a-5ab+1)= .
-6a3+10a3b-2a2
5x2+10x
-2x2+6xy
2m3-m2n
6. 计算:
(1) 4(a-b+1); (2) 3x(2x-y2)
(3) -3x(2x-5y+6z); (4) (-2a2)(-a-2b+c)
解:(1) 4(a-b+1)
=4a-4b+4;
(2)3x(2x-y2)=3x·2x+3x·(-y2)
=6x2-3xy2;
=2a3+4a2b-2a2c
6. 计算:
(1) 4(a-b+1); (2) 3x(2x-y2)
(3) -3x(2x-5y+6z); (4) (-2a2)(-a-2b+c)
(3)-3x(2x-5y+6z)
=-3x·(2x)+(-3x)·(-5y)+(-3x)·6z
=-6x2+15xy-18xz;
(4)(-2a2)(-a-2b+c)
=(-2a2)·(-a)+(-2a2)·(-2b)+(-2a2)·c
=2a3+4a2b-2a2c
7.化简求值:x2(x-1)-x(x2+x-1),其中,x= .
解:原式=x3-x2-x3-x2+x
=-2x2+x
当x= 时,原式=
8. 化简求值:x(x2-1)+2x2(x+1)-3x(2x-5),其中,x=-1.
解:原式=x3-x+2x3+2x2-6x2+15x
=3x3-4x2+14x
当x=-1时,
原式=3×(-1)3-4×(-1)2+14×(-1)
=-3-4-14
=-21
9.当m,n为何值时, x[x(x+m)+nx(x+1)+m] 的展开式中不含x2项和x3项?
解: x[x(x+m)+nx(x+1)+m]
= x(x2+mx+nx2+nx+m)
= (1+n)x3+ (m+n)x2+ mx,
因为展开式中不含x2项和x3项,
所以1+n=0,m+n=0,
解得n=-1,m=1.
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
