第九章 不等式与不等式组(复习课件)-七年级数学下册同步备课系列(人教版)
文档属性
| 名称 | 第九章 不等式与不等式组(复习课件)-七年级数学下册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 15:44:54 | ||
图片预览




文档简介
第9章 不等式与不等式组
章节复习
第五单元
01
03
04
02
05
举一反三
知识梳理
易错考点
高频考点
章节框图
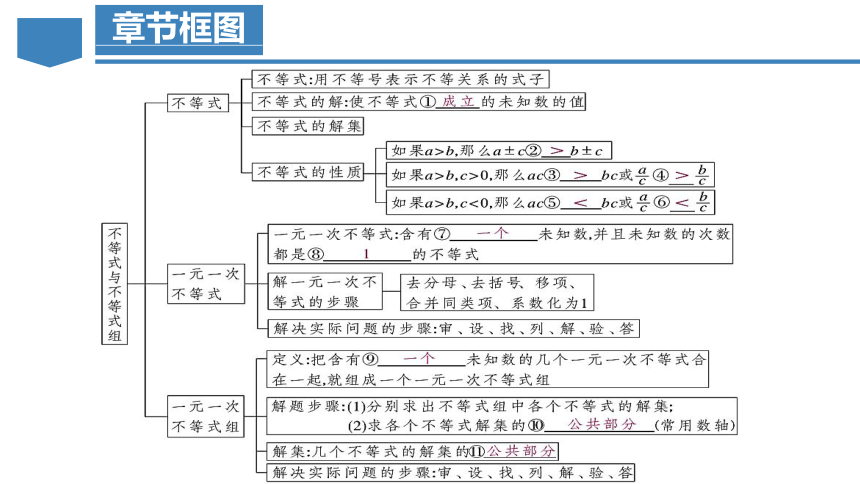
像????????????<????????和????????x>50这样用符号“<”或“>”表示大小关系的式子,叫做不等式.
?
(1)像a+2≠a-2这样用符号“≠”表示不等关系的式子也是不等式.
(2)不等式中可以含未知数,也可以不含未知数.例如:a+2>5,4b<6;
3<4,-1>-2.
(3)“≥”读作“大于或等于”或“不小于”
“≤”读作“小于或等于”或“不大于”
一、不等式的相关概念
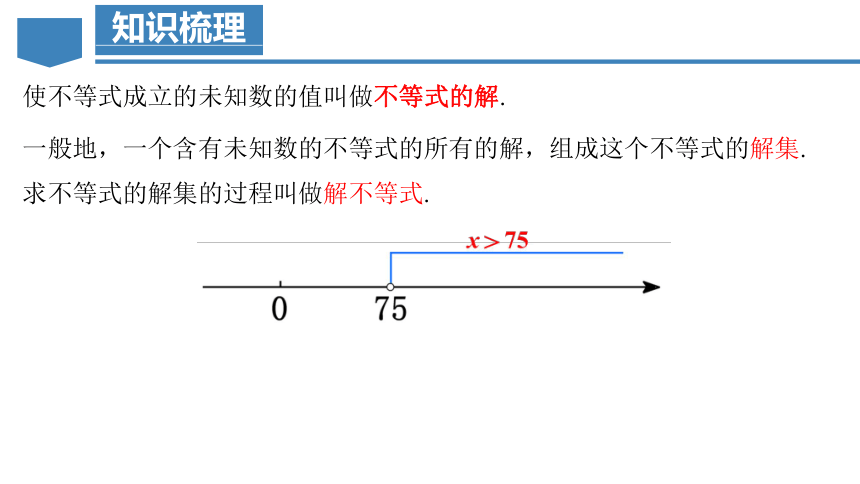
使不等式成立的未知数的值叫做不等式的解.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
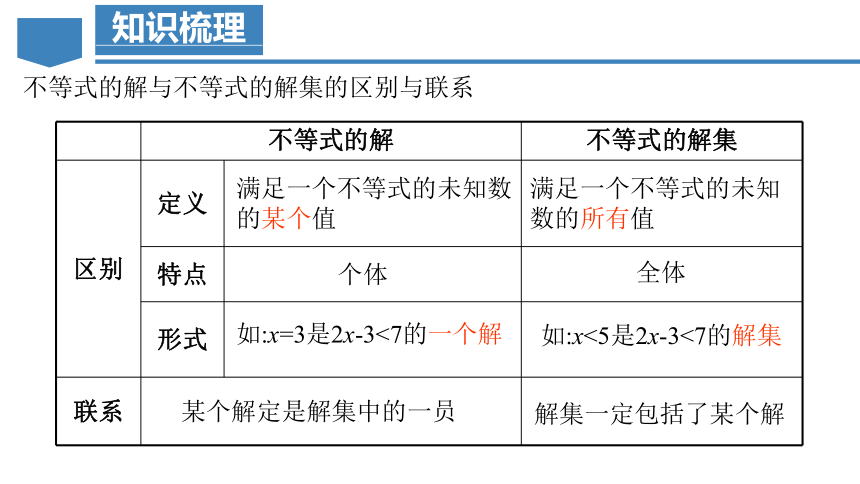
不等式的解
不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc (或????????>???????? ).
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc (或????????<???????? ).
?
二、不等式的性质
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
★解一元一次不等式的基本要求:
三、一元一次不等式及其解法
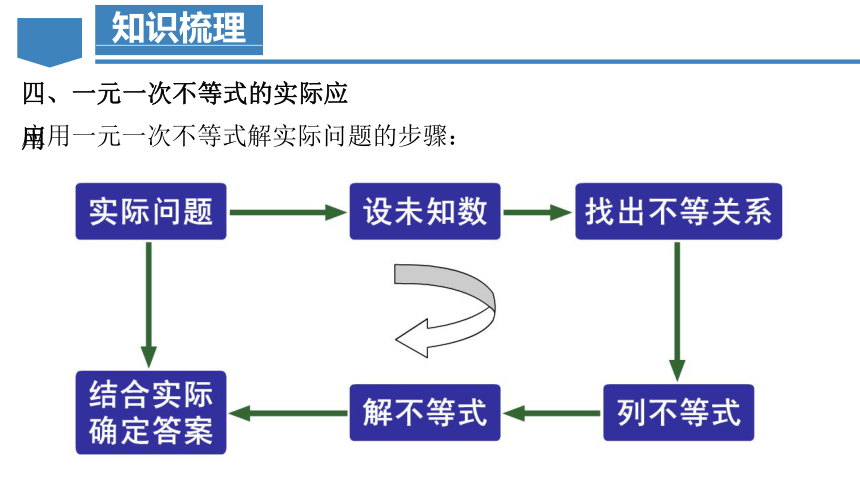
应用一元一次不等式解实际问题的步骤:
四、一元一次不等式的实际应用
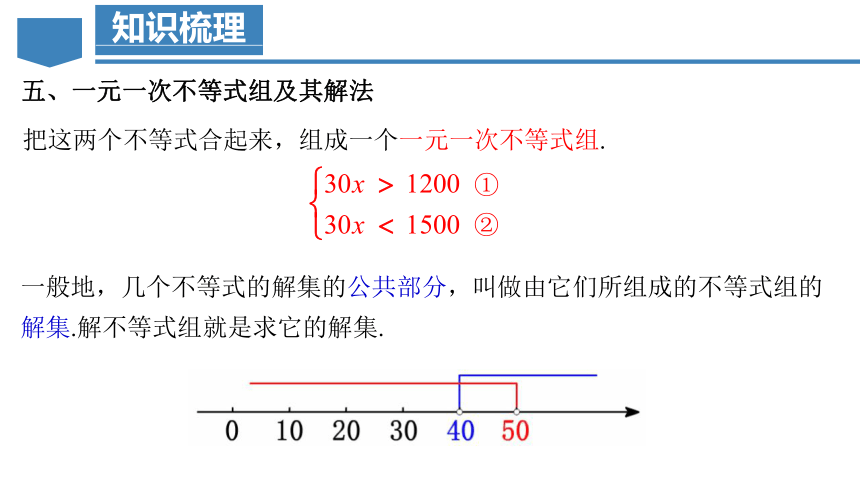
五、一元一次不等式组及其解法
把这两个不等式合起来,组成一个一元一次不等式组.
①
②
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.
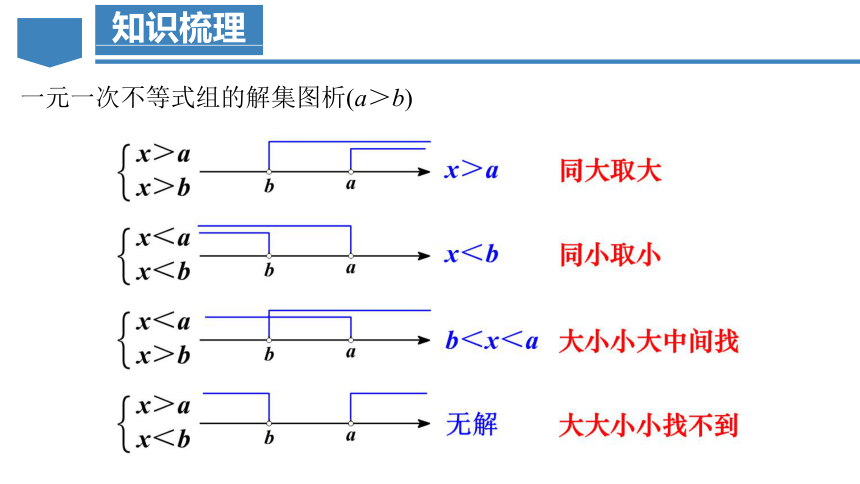
一元一次不等式组的解集图析(a>b)
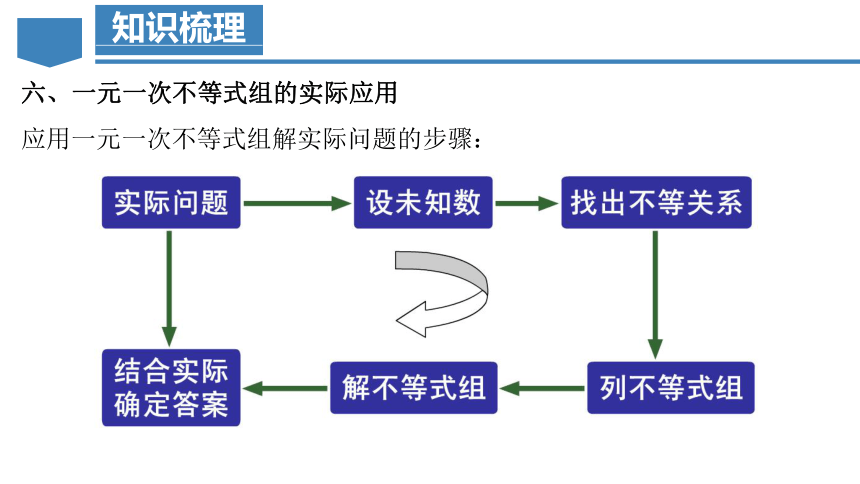
应用一元一次不等式组解实际问题的步骤:
六、一元一次不等式组的实际应用
高频考点一
不等式的性质
例1.若aA.a|m|>b|m| B.????????2?
C
【1-1】已知aA.a-1-2b C.12a+1<12b+1 D.ma>mb
【1-2】已知a>b,下列结论:①a2>ab;②a2>b2;③若b<0,则a+b<2b;④若b>0,则1????<1????.其中正确的个数是( )
A.1 B.2 C.3 D.4
?
D
A
高频考点二
一元一次不等式(组)的解法
例2.(1)解不等式4?????13-x>1,并在数轴上表示解集;
?
解:(1)去分母,得 4x-1-3x>3.
移项,得 4x-3x>3+1.
合并同类项,得 x>4.
这个不等式的解集在数轴上的表示如图所示.
高频考点二
一元一次不等式(组)的解法
例2. (2)解不等式组:2????+3?????2<4①????+32<2?????53+3?????② 并把解集在数轴上表示出来.
?
(2)解不等式①,得x<2.
解不等式②,得x>1.
所以,不等式组的解集为1这个不等式组的解集在数轴上的表示如图所示.
【2-1】不等式3(1-x)>2-4x的解集在数轴上表示正确的是( )
【2-2】不等式组2????>3????????+4>2的整数解是( )
A.0 B.- 1 C.-2 D.1
【2-3】现规定一种新的运算:m#n=4m-3n.例如3#2=4×3-3×2.若x#43<0,且x#(-4)≥0,则x的取值范围是___________.
?
A
-3≤x<1
B
【2-4】解不等式23x+12≥12x,并在数轴上表示其解集.
解:去分母,得 4x+3≥3x
移项、合并同类项,得x≥-3
这个不等式的解集在数轴上的表示如图所示.
?
【2-5】解不等式组:5?????6≤2????+3???①????4?1<?????33????????????????②
?
解:解不等式①,得x≤4.
解不等式②,得x>0.
所以,不等式组的解集是0高频考点三
确定不等式(组)中字母的值或范围
例3.若关于x的不等式组?????24<?????132?????????≤2?????有且只有两个整数解,则m的取值范围是____________.
?
解析:解不等式?????24<?????13,得x>-2.
解不等式2x-m≤2-x,得x≤2+????3.
因为原不等式组有且只有两个整数解,即-1,0,
所以0≤2+????3<1,解得-2≤m<1.
?
-2≤m<1
【3-1】若关于x的不等式组2?????2>2?????43?3????>?2?????????的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<-2 C.a>2 D.a≤2
【3-2】已知x=4是不等式ax-3a-1<0的解,x=2不是不等式ax-3a-1<0的解,则实数a的取值范围是_______.
?
A
a≤ -1
【3-3】已知关于x的不等式组2?????1<3????>????无解,则m的取值范围是_______.
【3-4】若关于x的不等式7x+9>2x+a的负整数解为-2,则a的取值范围是___________.
?
-6≤ a<-1
m≥2
高频考点四
一元一次不等式(组)的应用
例4.某市公交公司为落实“绿色出行,低碳环保”的城市发展理念,计划购买A,B两种型号的新型公交车,已知购买1辆A型公交车和2辆B型公交车需要165 万元,2辆A型公交车和3辆B型公交车需要270万元.
(1)A型公交车和B型公交车每辆各多少万元?
(2)公交公司计划购买A型公交车和B型公交车共140辆,且购买A型公交车的总费用不高于B型公交车的总费用,那么该公司最多购买多少辆A型公交车?
高频考点四
一元一次不等式(组)的应用
分析:(1)等量关系:购买1辆A型公交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
(2)不等关系:购买A型公交车的总费用不高于B型公交车的总费用.
解:(1)设A型公交车每辆x万元,B型公交车每辆y万元.
????+2????=1652????+3????=270
由题意,得 解得????=45????=60
答:A型公交车每辆45万元,B型公交车每辆60万元.
?
高频考点四
一元一次不等式(组)的应用
分析:(1)等量关系:购买1辆A型公交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
(2)不等关系:购买A型公交车的总费用不高于B型公交车的总费用.
(2)设该公司购买m辆A型公交车,则购买(140-m)辆B型公交车.
由题意,得 45m≤60(140-m).
解得 m≤80.
答:该公司最多购买80辆A型公交车.
【4-1】一次数学基础知识竞赛共有30道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,某同学获得优秀(90分或90分以上),则这位同学至少答对了_____道题.
【4-2】世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人,则一个团队至少要有_____人进公园,买40张门票反而合算.
24
33
高频考点四
一元一次不等式(组)的应用
【4-3】某市垃圾处理厂利用焚烧垃圾产生的热能发电.有A,B两个焚烧炉,每个焚烧炉每天均焚烧100t垃圾,每焚烧1t垃圾,A焚烧炉比B焚烧炉多发电50度,A,B焚烧炉每天共发电55000度.
(1)焚烧1 t垃圾,A焚烧炉和B焚烧炉各发电多少度?
(2)若经过改进工艺,与改进工艺之前相比,每焚烧1t垃圾,A焚烧炉和B焚烧炉的发电量分别增加a%和2a%,则A,B焚烧炉每天共发电至少增加(5+a)%,求a的最小值.
高频考点四
一元一次不等式(组)的应用
(1)焚烧1 t垃圾,A焚烧炉和B焚烧炉各发电多少度?
解:(1)设焚烧1t垃圾,A焚烧炉发电m度,B焚烧炉发电n度.
根据题意,得?????????=50100????+????=55000
解得????=300????=250
答:焚烧1t垃圾,A焚烧炉发电300度,B焚烧炉发电250度.
?
高频考点四
一元一次不等式(组)的应用
(2)若经过改进工艺,与改进工艺之前相比,每焚烧1t垃圾,A焚烧炉和B焚烧炉的发电量分别增加a%和2a%,则A,B焚烧炉每天共发电至少增加(5+a)%,求a的最小值.
(2)依题意有100×300(1+a%)+100×250(1+2a%)≥55000[1+(5+a)%],
解得a≥11.
所以a的最小值为11.
例5. 状状准备在重阳节购买鲜花到敬老院看望老人,现将自己在劳动课上制作的竹篮和陶罐拿到学校的“跳蚤市场”出售,如图是购买者的出价:(1)根据对话内容,求状状出售的竹篮和陶罐数量;
(2)状状接受了成成的报价,交易后到花
店购买单价为5元/束的鲜花,剩余的钱
不超过20元,求有哪几种购买方案.
高频考点四
一元一次不等式(组)的应用
(1)根据对话内容,求状状出售的竹篮和陶罐数量;
高频考点四
一元一次不等式(组)的应用
解:(1)设出售竹篮x个,陶罐y个.
根据题意,得 5????+12????=616????+10????=60
解得 ????=5????=3
故状状出售的竹篮有5个,陶罐有3个.
?
(2)状状接受了成成的报价,交易后到花店购买单价为5元/束的鲜花,剩余的钱不超过20元,求有哪几种购买方案.
高频考点四
一元一次不等式(组)的应用
(2)设购买鲜花a束.
根据题意,得0<61-5a≤20,
解得8.2≤a<12.2.
因为a为整数,所以共有4种购买方案:
方案一:购买鲜花9束;方案二:购买鲜花10束;
方案三:购买鲜花11束;方案四:购买鲜花12束.
【5-1】某绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A,B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如表:
(注:不同种植户种植的同类蔬菜每公顷平均收入相等)
(1)求种植A,B两类蔬菜每公顷平均收入各是多少元.
(2)某种植户准备租20公顷地用来种植A,B两类蔬菜,为了使总收入不低于630000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的所有种植方案.
(1)求种植A,B两类蔬菜每公顷平均收入各是多少元.
解:(1)设种植A类蔬菜每公顷平均收入是
x元,种植B类蔬菜每公顷平均收入是y元.
依题意,得
3????+????=1250002????+3????=165000
解得????=30000????=35000
答:种植A类蔬菜每公顷平均收入是30000元,种植B类蔬菜每公顷平均收入是35000元.
?
(2)某种植户准备租20公顷地用来种植A,B两类蔬菜,为了使总收入不低于630000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的所有种植方案.
(2)设种植A类蔬菜m公顷,则种植B类蔬菜
(20-m)公顷.
依题意,得????>20?????30000????+3500020?????≥630000
解得10?
(2)某种植户准备租20公顷地用来种植A,B两类蔬菜,为了使总收入不低于630000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的所有种植方案.
因为m为整数,
所以m可取11,12,13,14,
所以该种植户共有4种种植方案.
方案一:种植A类蔬菜11公顷,B类蔬菜9公顷;方案二:种植A类蔬菜12公顷,B类蔬菜8公顷;方案三:种植A类蔬菜13公顷,B类蔬菜7公顷;方案四:种植A类蔬菜14公顷,B类蔬菜6公顷.
(3)在(2)的条件下,该种植户选择哪种方案,能使总收入最大?最大总收入是多少?
(3)选择方案一获得的总收入为30000×11+35000×9= 645000(元);
选择方案二获得的总收入为30000×12+35000×8 = 640000(元);
选择方案三获得的总收入为30000×13+35000×7= 635000(元);
选择方案四获得的总收入为30000×14+35000×6= 630000(元).
因为645000>640000>635000>630000,
所以该种植户选择方案一,能使总收入最大,最大总收入是645000元.
易错考点一
在运用不等式的性质时考虑不周全
例1.若a>b,c为实数,则ac2____bc2.
正解:因为a>b,c2≥0,
所以当c2>0时,ac2 >bc2;
当c2=0时,ac2=bc2.
所以ac2≥bc2.
故答案为≥.
≥
易错考点二
对不等式的解与解集的定义理解不透彻
例2.已知不等式x<5的解也是关于x的不等式2????+????3<1的解,求m满足的条件.
?
正解:解不等式2????+????3<1,得x<3?????2.
根据题意,得3?????2≥5,
解得m≤-7.
?
易错考点三
解一元一次不等式时常见的错误
例3.解不等式:2?????13?5????+12 ≤1
?
正解:去分母,得 2(2x-1)-3(5x+1)≤6.
去括号,得 4x-2-15x-3≤6.
移项,得 4x-15x≤6+2+3.
合并同类项,得 -11x≤11.
系数化为1,得 x≥-1.2
易错考点四
确定不等式(组)中字母的取值范围时出错
例4.若关于x的不等式组?????3?????2≤4????+2????3????>无解,则a的取值范围是( )
A.a1 D.a≥1
?
B
章节复习
第五单元
01
03
04
02
05
举一反三
知识梳理
易错考点
高频考点
章节框图
像????????????<????????和????????x>50这样用符号“<”或“>”表示大小关系的式子,叫做不等式.
?
(1)像a+2≠a-2这样用符号“≠”表示不等关系的式子也是不等式.
(2)不等式中可以含未知数,也可以不含未知数.例如:a+2>5,4b<6;
3<4,-1>-2.
(3)“≥”读作“大于或等于”或“不小于”
“≤”读作“小于或等于”或“不大于”
一、不等式的相关概念
使不等式成立的未知数的值叫做不等式的解.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
不等式的解
不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc (或????????>???????? ).
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc (或????????<???????? ).
?
二、不等式的性质
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
★解一元一次不等式的基本要求:
三、一元一次不等式及其解法
应用一元一次不等式解实际问题的步骤:
四、一元一次不等式的实际应用
五、一元一次不等式组及其解法
把这两个不等式合起来,组成一个一元一次不等式组.
①
②
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.
一元一次不等式组的解集图析(a>b)
应用一元一次不等式组解实际问题的步骤:
六、一元一次不等式组的实际应用
高频考点一
不等式的性质
例1.若a
C
【1-1】已知a
【1-2】已知a>b,下列结论:①a2>ab;②a2>b2;③若b<0,则a+b<2b;④若b>0,则1????<1????.其中正确的个数是( )
A.1 B.2 C.3 D.4
?
D
A
高频考点二
一元一次不等式(组)的解法
例2.(1)解不等式4?????13-x>1,并在数轴上表示解集;
?
解:(1)去分母,得 4x-1-3x>3.
移项,得 4x-3x>3+1.
合并同类项,得 x>4.
这个不等式的解集在数轴上的表示如图所示.
高频考点二
一元一次不等式(组)的解法
例2. (2)解不等式组:2????+3?????2<4①????+32<2?????53+3?????② 并把解集在数轴上表示出来.
?
(2)解不等式①,得x<2.
解不等式②,得x>1.
所以,不等式组的解集为1
【2-1】不等式3(1-x)>2-4x的解集在数轴上表示正确的是( )
【2-2】不等式组2????>3????????+4>2的整数解是( )
A.0 B.- 1 C.-2 D.1
【2-3】现规定一种新的运算:m#n=4m-3n.例如3#2=4×3-3×2.若x#43<0,且x#(-4)≥0,则x的取值范围是___________.
?
A
-3≤x<1
B
【2-4】解不等式23x+12≥12x,并在数轴上表示其解集.
解:去分母,得 4x+3≥3x
移项、合并同类项,得x≥-3
这个不等式的解集在数轴上的表示如图所示.
?
【2-5】解不等式组:5?????6≤2????+3???①????4?1<?????33????????????????②
?
解:解不等式①,得x≤4.
解不等式②,得x>0.
所以,不等式组的解集是0
确定不等式(组)中字母的值或范围
例3.若关于x的不等式组?????24<?????132?????????≤2?????有且只有两个整数解,则m的取值范围是____________.
?
解析:解不等式?????24<?????13,得x>-2.
解不等式2x-m≤2-x,得x≤2+????3.
因为原不等式组有且只有两个整数解,即-1,0,
所以0≤2+????3<1,解得-2≤m<1.
?
-2≤m<1
【3-1】若关于x的不等式组2?????2>2?????43?3????>?2?????????的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<-2 C.a>2 D.a≤2
【3-2】已知x=4是不等式ax-3a-1<0的解,x=2不是不等式ax-3a-1<0的解,则实数a的取值范围是_______.
?
A
a≤ -1
【3-3】已知关于x的不等式组2?????1<3????>????无解,则m的取值范围是_______.
【3-4】若关于x的不等式7x+9>2x+a的负整数解为-2,则a的取值范围是___________.
?
-6≤ a<-1
m≥2
高频考点四
一元一次不等式(组)的应用
例4.某市公交公司为落实“绿色出行,低碳环保”的城市发展理念,计划购买A,B两种型号的新型公交车,已知购买1辆A型公交车和2辆B型公交车需要165 万元,2辆A型公交车和3辆B型公交车需要270万元.
(1)A型公交车和B型公交车每辆各多少万元?
(2)公交公司计划购买A型公交车和B型公交车共140辆,且购买A型公交车的总费用不高于B型公交车的总费用,那么该公司最多购买多少辆A型公交车?
高频考点四
一元一次不等式(组)的应用
分析:(1)等量关系:购买1辆A型公交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
(2)不等关系:购买A型公交车的总费用不高于B型公交车的总费用.
解:(1)设A型公交车每辆x万元,B型公交车每辆y万元.
????+2????=1652????+3????=270
由题意,得 解得????=45????=60
答:A型公交车每辆45万元,B型公交车每辆60万元.
?
高频考点四
一元一次不等式(组)的应用
分析:(1)等量关系:购买1辆A型公交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
(2)不等关系:购买A型公交车的总费用不高于B型公交车的总费用.
(2)设该公司购买m辆A型公交车,则购买(140-m)辆B型公交车.
由题意,得 45m≤60(140-m).
解得 m≤80.
答:该公司最多购买80辆A型公交车.
【4-1】一次数学基础知识竞赛共有30道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,某同学获得优秀(90分或90分以上),则这位同学至少答对了_____道题.
【4-2】世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人,则一个团队至少要有_____人进公园,买40张门票反而合算.
24
33
高频考点四
一元一次不等式(组)的应用
【4-3】某市垃圾处理厂利用焚烧垃圾产生的热能发电.有A,B两个焚烧炉,每个焚烧炉每天均焚烧100t垃圾,每焚烧1t垃圾,A焚烧炉比B焚烧炉多发电50度,A,B焚烧炉每天共发电55000度.
(1)焚烧1 t垃圾,A焚烧炉和B焚烧炉各发电多少度?
(2)若经过改进工艺,与改进工艺之前相比,每焚烧1t垃圾,A焚烧炉和B焚烧炉的发电量分别增加a%和2a%,则A,B焚烧炉每天共发电至少增加(5+a)%,求a的最小值.
高频考点四
一元一次不等式(组)的应用
(1)焚烧1 t垃圾,A焚烧炉和B焚烧炉各发电多少度?
解:(1)设焚烧1t垃圾,A焚烧炉发电m度,B焚烧炉发电n度.
根据题意,得?????????=50100????+????=55000
解得????=300????=250
答:焚烧1t垃圾,A焚烧炉发电300度,B焚烧炉发电250度.
?
高频考点四
一元一次不等式(组)的应用
(2)若经过改进工艺,与改进工艺之前相比,每焚烧1t垃圾,A焚烧炉和B焚烧炉的发电量分别增加a%和2a%,则A,B焚烧炉每天共发电至少增加(5+a)%,求a的最小值.
(2)依题意有100×300(1+a%)+100×250(1+2a%)≥55000[1+(5+a)%],
解得a≥11.
所以a的最小值为11.
例5. 状状准备在重阳节购买鲜花到敬老院看望老人,现将自己在劳动课上制作的竹篮和陶罐拿到学校的“跳蚤市场”出售,如图是购买者的出价:(1)根据对话内容,求状状出售的竹篮和陶罐数量;
(2)状状接受了成成的报价,交易后到花
店购买单价为5元/束的鲜花,剩余的钱
不超过20元,求有哪几种购买方案.
高频考点四
一元一次不等式(组)的应用
(1)根据对话内容,求状状出售的竹篮和陶罐数量;
高频考点四
一元一次不等式(组)的应用
解:(1)设出售竹篮x个,陶罐y个.
根据题意,得 5????+12????=616????+10????=60
解得 ????=5????=3
故状状出售的竹篮有5个,陶罐有3个.
?
(2)状状接受了成成的报价,交易后到花店购买单价为5元/束的鲜花,剩余的钱不超过20元,求有哪几种购买方案.
高频考点四
一元一次不等式(组)的应用
(2)设购买鲜花a束.
根据题意,得0<61-5a≤20,
解得8.2≤a<12.2.
因为a为整数,所以共有4种购买方案:
方案一:购买鲜花9束;方案二:购买鲜花10束;
方案三:购买鲜花11束;方案四:购买鲜花12束.
【5-1】某绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A,B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如表:
(注:不同种植户种植的同类蔬菜每公顷平均收入相等)
(1)求种植A,B两类蔬菜每公顷平均收入各是多少元.
(2)某种植户准备租20公顷地用来种植A,B两类蔬菜,为了使总收入不低于630000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的所有种植方案.
(1)求种植A,B两类蔬菜每公顷平均收入各是多少元.
解:(1)设种植A类蔬菜每公顷平均收入是
x元,种植B类蔬菜每公顷平均收入是y元.
依题意,得
3????+????=1250002????+3????=165000
解得????=30000????=35000
答:种植A类蔬菜每公顷平均收入是30000元,种植B类蔬菜每公顷平均收入是35000元.
?
(2)某种植户准备租20公顷地用来种植A,B两类蔬菜,为了使总收入不低于630000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的所有种植方案.
(2)设种植A类蔬菜m公顷,则种植B类蔬菜
(20-m)公顷.
依题意,得????>20?????30000????+3500020?????≥630000
解得10
(2)某种植户准备租20公顷地用来种植A,B两类蔬菜,为了使总收入不低于630000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的所有种植方案.
因为m为整数,
所以m可取11,12,13,14,
所以该种植户共有4种种植方案.
方案一:种植A类蔬菜11公顷,B类蔬菜9公顷;方案二:种植A类蔬菜12公顷,B类蔬菜8公顷;方案三:种植A类蔬菜13公顷,B类蔬菜7公顷;方案四:种植A类蔬菜14公顷,B类蔬菜6公顷.
(3)在(2)的条件下,该种植户选择哪种方案,能使总收入最大?最大总收入是多少?
(3)选择方案一获得的总收入为30000×11+35000×9= 645000(元);
选择方案二获得的总收入为30000×12+35000×8 = 640000(元);
选择方案三获得的总收入为30000×13+35000×7= 635000(元);
选择方案四获得的总收入为30000×14+35000×6= 630000(元).
因为645000>640000>635000>630000,
所以该种植户选择方案一,能使总收入最大,最大总收入是645000元.
易错考点一
在运用不等式的性质时考虑不周全
例1.若a>b,c为实数,则ac2____bc2.
正解:因为a>b,c2≥0,
所以当c2>0时,ac2 >bc2;
当c2=0时,ac2=bc2.
所以ac2≥bc2.
故答案为≥.
≥
易错考点二
对不等式的解与解集的定义理解不透彻
例2.已知不等式x<5的解也是关于x的不等式2????+????3<1的解,求m满足的条件.
?
正解:解不等式2????+????3<1,得x<3?????2.
根据题意,得3?????2≥5,
解得m≤-7.
?
易错考点三
解一元一次不等式时常见的错误
例3.解不等式:2?????13?5????+12 ≤1
?
正解:去分母,得 2(2x-1)-3(5x+1)≤6.
去括号,得 4x-2-15x-3≤6.
移项,得 4x-15x≤6+2+3.
合并同类项,得 -11x≤11.
系数化为1,得 x≥-1.2
易错考点四
确定不等式(组)中字母的取值范围时出错
例4.若关于x的不等式组?????3?????2≤4????+2????3????>无解,则a的取值范围是( )
A.a
?
B
